考虑压强、速率影响的FPS材料动摩擦试验与模拟研究
李 宁, 王 徐, 李忠献
(1. 天津大学 建筑工程学院,天津 300072; 2. 天津大学 滨海土木工程结构与安全教育部重点实验室,天津 300072;3. 天津大学 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室,天津 300350)
近年来减隔震技术发展日趋成熟,减震元件可耗散地震能量,隔震装置还可延长结构自振周期,通过合理设计可以有效避免结构震损。滑动摩擦技术工艺简单、可靠且效果良好,其中滑动摩擦摆(friction pendulum system,FPS)装置作为减隔震装置的一种,自Dario等[1-3]提出后,由于其具有很好的自复位能力,受到广泛的研究与设计人员的青睐。
鉴于滑动面的摩擦材料关系到FPS的抗震性能,对此众多学者进行了大量的研究。Constantinou等[4]对动态条件下的钢材与PTFE(Polytetrafluoroethylene)界面摩擦进行了研究,试验结果表明,随着地面运动加速度的减小,钢材与PTFE界面的摩擦减小,但随法向压力增大摩擦增大。Tyler[5]测试了380 mm/s滑动速度下PTFE的摩擦因数,发现随滑动速度的增加和压力的降低而摩擦因数增大。Mokha等[6]进行了500 mm/s的滑动摩擦试验,观察到滑动速度在100~200 mm/s时μ迅速增加,而在较高的滑动速度下μ近似恒定,并提出了指数函数模型。黄亮等[7]介绍了一种摩擦界面为二硫化钼的新型滑动支座,研究其不同压强、不同频率下摩擦因数变化,分析表明压强增大摩擦因数减小,加载频率增大摩擦因数增大。Kumar等[8]研究了PTFE材料受速率、温度、压强影响的摩擦行为,并提出一种摩擦因数相关行为模型。荣强等[9]研究了PTFE摩擦因数在不同影响因素下的变化规律,研究表明摩擦因数与竖向压力、速度以及激励频率有关,同时提出一个新的力学拟合模型。洪越等[10]提出变曲率摩擦摆支座,研究结果表明加载频率越大摩擦因数越大。综上,FPS摩擦因数受滑动速率、压力、压强、温度等因素的影响被研究人员广泛关注,并提出了相应数学模型(指数、对数函数等)进行建模表征,但研究对象多为等效摩擦因数的变化规律,瞬时摩擦效应尚不清楚,瞬态摩擦因数的变化规律尚有待探讨。
Kim等[11]研究了混入不同含量的纳米二氧化钛的聚偏二氯乙烯(polyvinylidene chloride,PVDF)的摩擦性能,并通过易损性分析提出了液化天然气储罐最优摩擦因数的确定方法。而后又研究了经MgO强化的PVDF的摩擦性能[12],标定摩擦因数处于0.055 7~0.119 1。Han等[13]测试了耐久性更好的PTFE织物的摩擦性能,并用于变频摩擦摆中。目前越来越多的聚合物和新材料等被提出、测试,并应用于FPS中[14]。工程上纯PTFE耐磨性能较差,降低其使用寿命,因此摩擦材料的研究与选用显得尤为关键。
分子动力学模拟在材料的微观摩擦中已有一定的应用。尹宇航等[15]采用分子动力学模拟研究了经石墨烯改性的PTFE与Cu摩擦性能,结果表明经过改性后的材料摩擦因数、机械性能均有明显的提高。Lahiri等[16]研究了石墨烯增强聚乙烯在纳米尺度上的摩擦学行为,结果表明,石墨烯的含量从w=0.1%提高到w=1.0%时,聚合物基体的耐磨性不断提高。因此分子动力学方法应用于界面摩擦因数预测的具有一定的可行性。
FPS摩擦材料的研发与改良一直是热点研究方向之一;材料的循环退化现象影响其耗能能力、摩擦副随运动方向改变时产生的黏滞滑移效应可能导致结构响应增大[17];考虑到动摩擦因数变化特性影响结构响应,且大地震作用下摩擦摆速率较大,而试验条件有限,大速率下摩擦实测仍存在困难。因此研究FPS材料的摩擦行为,确定摩擦因数与瞬时滑动速率、压强的关系,对FPS支座的研究、应用尤为重要。
本文选取5种常见的热塑性工程塑料作为摩擦材料进行试验研究。主要包括:①探究了不同滑动速率与不同压强下不同材料的循环退化、黏滞滑移程度和材料的耐磨性能;②探究了摩擦因数与瞬时滑动速率、压强之间的关系;③针对PTFE与钢二者界面摩擦进行分子动力学模拟,验证小速率下模拟效果,而后进行试验无法实现的大速率下摩擦因数预测。
1 摩擦材料试验
1.1 试验简介
本文选取了5种常见的热塑性工程塑料,材料厚度为8 mm,切割成矩形(6 mm×5.2 mm)。选用的摩擦材料块材如图1所示。

图1 5种不同摩擦材料样片Fig.1 Samples of the 5 different friction material
本试验采用MTS液压伺服作动器施加水平位移(反力和位移值通过控制系统记录)。竖向力采用液压千斤顶施加,并通过支座底安装的2支轮辐传感器测量,千斤顶上部安装无摩擦滚动滑车实现平动,如图2所示。摩擦材料上部压强为10~26 MPa(间隔4 MPa),采用正弦加载准则,循环加载6次[18]。加载工况如表1所示。工况命名:PTFE-S18-100表示PTFE在竖向压强为18 MPa、滑动速率峰值为100 mm/s的测试。
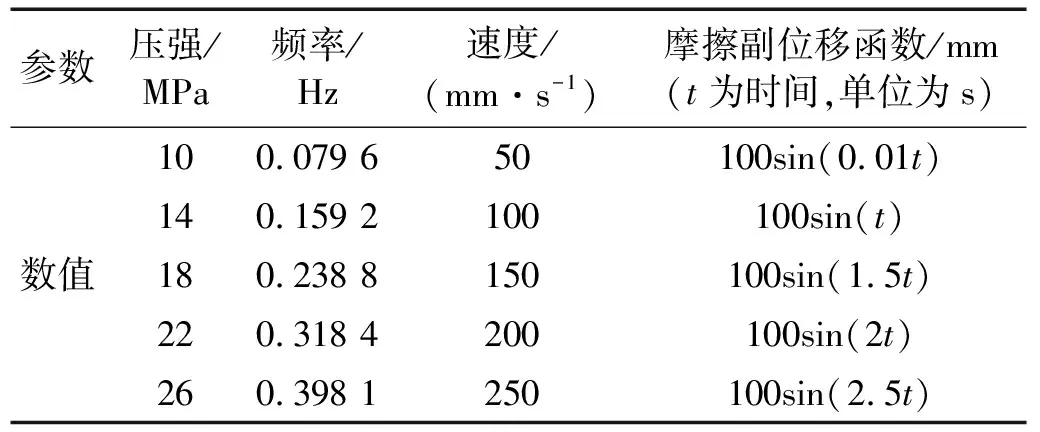
表1 试验工况表Tab.1 Test conditions table

图2 试验装置图(mm)Fig.2 Loading test device diagram (mm)
2 试验结果与讨论
2.1 循环退化
为说明循环退化情况,选取5种材料在竖向压强为18 MPa,峰值速率300 mm/s时,摩擦因数、摩擦力与位移的关系曲线如图3所示。随着加载周次增加,5种材料的摩擦因数均出现衰减,不同材料的衰减程度存在差异。
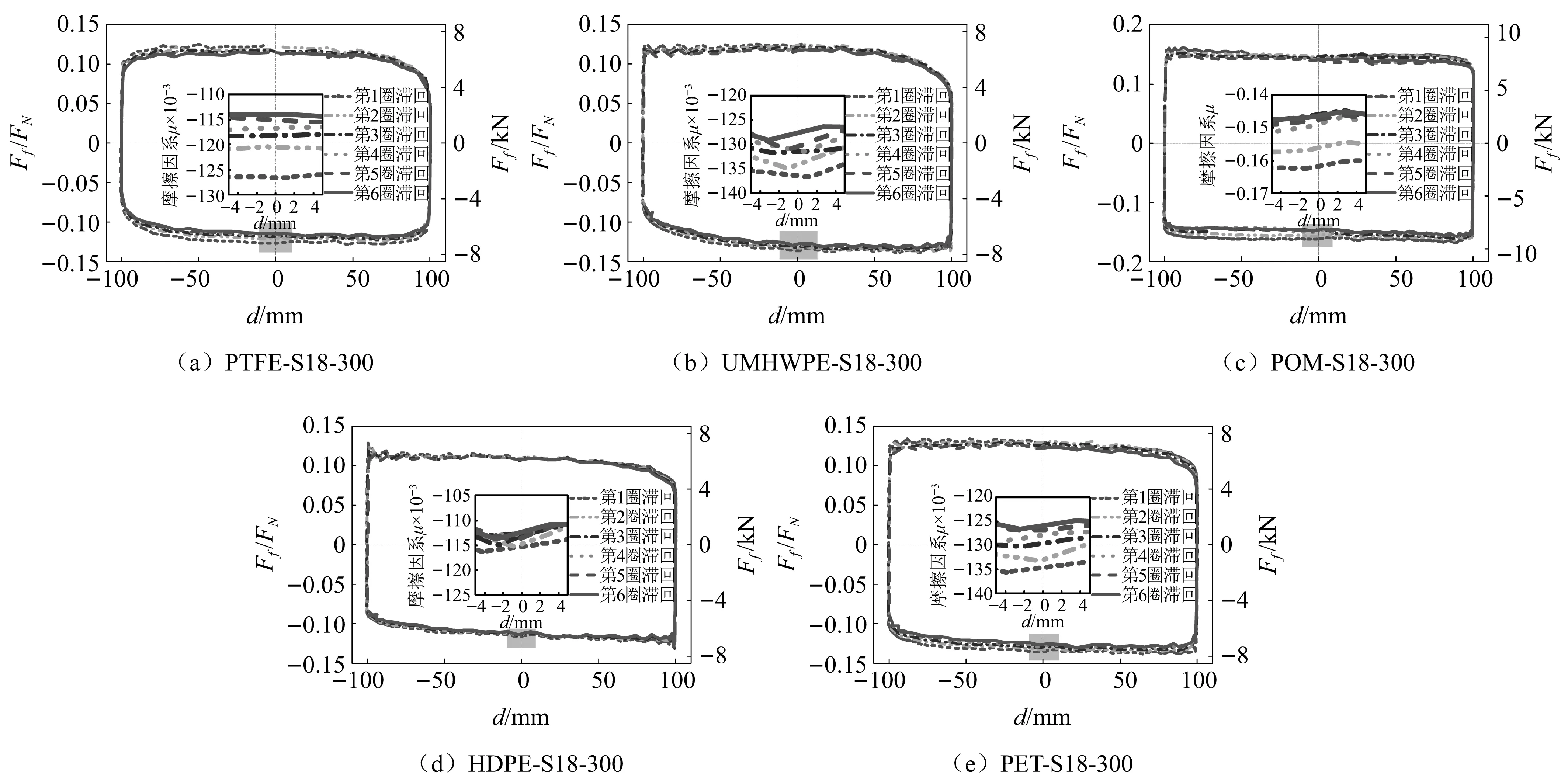
图3 摩擦因数、摩擦力与位移关系曲线Fig.3 Relation curves of friction coefficient, friction force and displacement
为了评价摩擦因数的循环衰减程度(循环退化效应),采用式(1)定量评估
(1)
式中,μpeak,1,μpeak,2,μpeak,11与μpeak,12分别为第1、第2、第11与第12个半程往复的峰值速率下的摩擦因数。
5种材料不同峰值滑动速率、压强下的ks汇总,如表2所示。随着滑动速率、压强的增大材料循环退化现象整体呈增大趋势。POM循环退化现象明显且离散程度大,不同滑动速率、压强下ks均值分别为0.937与0.911;方差分别为0.017 0与0.078 4;UMHWPE与HDPE循环退化现象较弱且离散度小。

表2 不同材料不同滑动速率、不同压强下ks汇总表Tab.2 ks summary table under different sliding rates and pressures of different materials
2.2 黏滞滑移
黏滞滑移指摩擦力随着滑行距离或时间突发的一种波动现象,表现为摩擦力与时间关系曲线呈锯齿状。HDPE在滑动速率峰值为200 mm/s的摩擦因数与位移、速度关系曲线如图4所示。

图4 HDPE的1/2往复μ与位移、滑动速率关系曲线Fig.4 Relationship curves between μ and displacement and loading rate in the first half cycle of HDPE
5种热塑性工程塑料的摩擦因数与瞬时速度之间均存在不同程度的黏滞滑移现象,由式(2)定量评估
(2)
式中,μmax,1,μmax,2和μpeak,1,μpeak,2分别为第1、第2半往复的摩擦因数最大值和峰值速率时的摩擦因数。
计算得kv如表3所示。由表3可知,POM随着滑动速率增大黏滞滑移越明显;除POM、HDPE随着压强增大黏结滑移减弱,其余材料均保持相对稳定。HDPE黏滞滑移现象明显,不同滑动速率、压强下kv均值分别为1.162 4与1.147 0。

表3 不同材料不同滑动速率与不同压强下kv汇总表Tab.3 kv summary table of different materials at different sliding rates and different pressures
2.3 耐磨性能
FPS的摩擦材料应具有良好的耐磨性能。根据GB/T 37358—2019《建筑摩擦摆隔震支座》[19]进行耐磨性能测试,取三次线磨损率均值作为磨损率评价指标,总滑动位移为6 m。根据式(3)计算材料线磨损率
(4)
式中:m0为材料初始质量;m为试验后质量;ρ为材料密度。5种材料的线磨损率结果如表4所示。
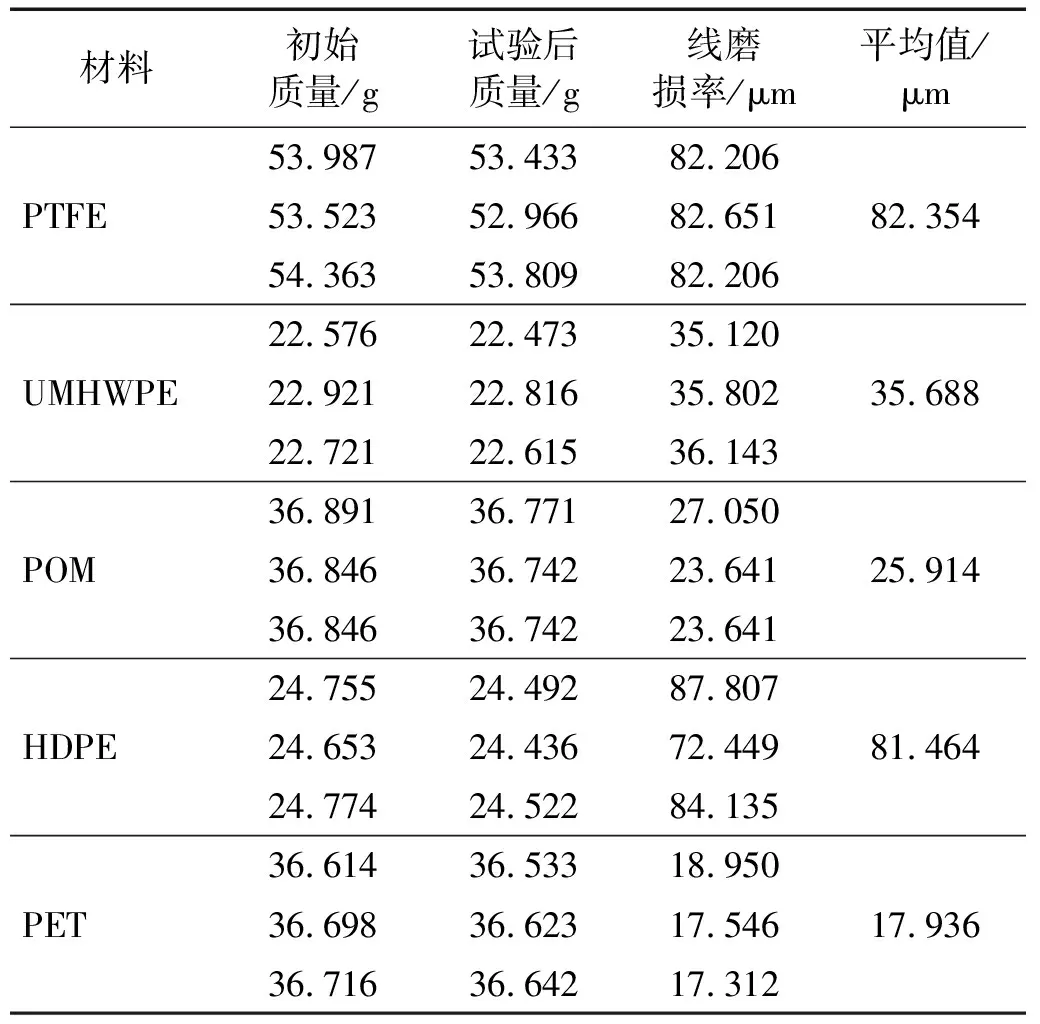
表4 5种材料的线磨损率试验结果Tab.4 Test results of linear wear rate for five materials
由表4可知,PET的耐磨性能最优,线磨损率为17.936 μm,POM和UMHWPE次之,PTFE和HDPE较差。结合1.1节研究,考虑到PTFE在工程上应用广泛,因此可将PTFE和UMHWPE与PET作为备选材料进行进一步研究。限于篇幅,将PET摩擦因数与速率、位移关系曲线绘出如图5所示,观察加速摩擦阶段和减速阶段数据可知,测试的5种材料均存在摩擦因数不可逆现象,即摩擦因数μ对于瞬时速率并不是一个可逆函数,加速摩擦时摩擦因数高于减速摩擦,这也是多数率模型考虑摩擦效应时,存在的困难之一。

图5 PET摩擦因数与速率、位移关系曲线Fig.5 Relation curve of PET friction coefficient with rate and displacement
2.4 瞬时滑动速率对摩擦因数的影响与模型拟合
通过分析不同材料试验结果可知,减速摩擦阶段摩擦因数与速率的关系曲线比较稳定,保守选用减速段数据进行分析。为减小磨损以及温度变化等因素造成的影响,采用式(4)对数据进行处理
(4)
式中:μ为试验测得的材料摩擦因数;μpeak,i为第i个周期所对应的峰值速率下的摩擦因数。
采用指数函数模型与对数函数模型对摩擦因数与瞬时速率进行拟合。忽略速率低于3 mm/s对对数函数模型的影响,拟合公式如式(5)、式(6)所示
(5)
(6)
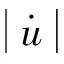
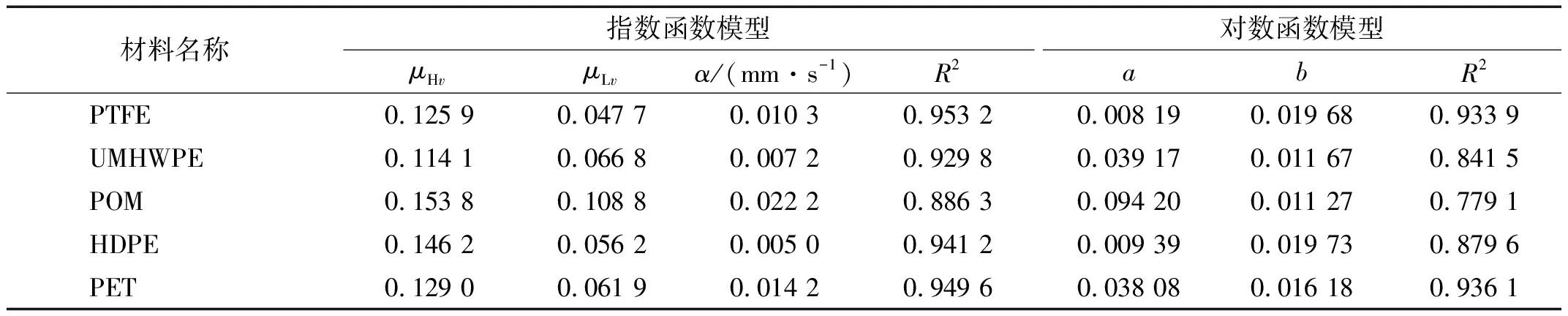
表5 摩擦因数与速率指数函数模型拟合参数表Tab.5 Fitting parameters of friction coefficient and rate exponential function model

图6 摩擦因数与速率关系指数、对数函数拟合Fig.6 Exponential and logarithmic fitting of friction coefficient and velocity
2.5 压强对摩擦因数的影响与模型拟合
不同材料在不同压强下的摩擦因数及拟合结果,如图7所示。当压强从14 MPa增加到26 MPa,PTFE低速时摩擦因数从0.068 5减小至0.052 1,降幅约20%;高速时摩擦因数从0.166减小至0.123,降幅约25.9%;UMHWPE低速时摩擦因数从0.070 6减小至0.061 81,降幅约12.5%,高速时摩擦因数从0.123 6减小至0.102 5,降幅约17.07%;PET低速时摩擦因数从0.062 6减小至0.053 9,降幅为10.7%,高速时摩擦因数从0.145 3减小至0.115 1,降幅为20.8%。材料摩擦因数随着压强的增大而减小,高速下压强对摩擦因数的影响大于低速下的影响。
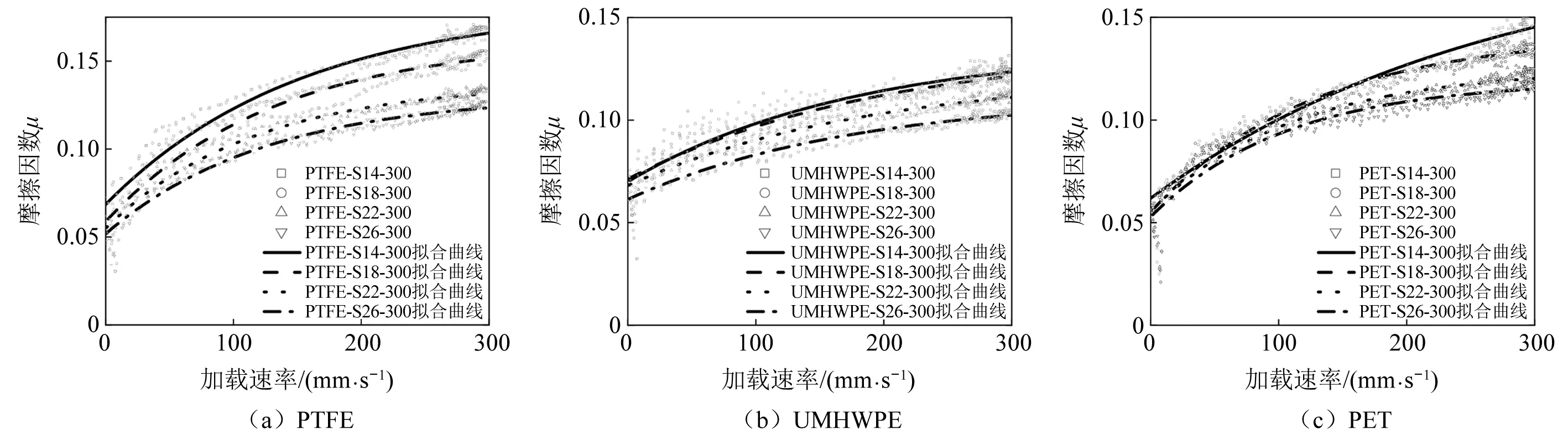
图7 不同压强下材料摩擦因数与速率关系Fig.7 Relationship between friction coefficient and velocity of materials at different pressures
考虑滑动速率、竖向压力对摩擦材料共同影响,根据Constantinou等的研究结果,采用式(7)对瞬时滑动速率、竖向压强共同影响下的摩擦因数进行建模拟合。
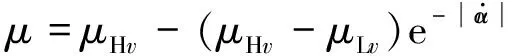
(7)
式中:P为压强;a,Δμ为压强参数;μHv0为初始高速摩擦下摩擦因数。对1.1节中的备选摩擦材料PTFE,UMHWPE与PET进行拟合,表6为试验测得的参数结果(瞬时速率范围0~300 mm/s),图8、图9为PTFE与PET拟合曲线,可知所采用的模型拟合结果较好。

表6 拟合曲线参数表Tab.6 Parameters of the fitting curve
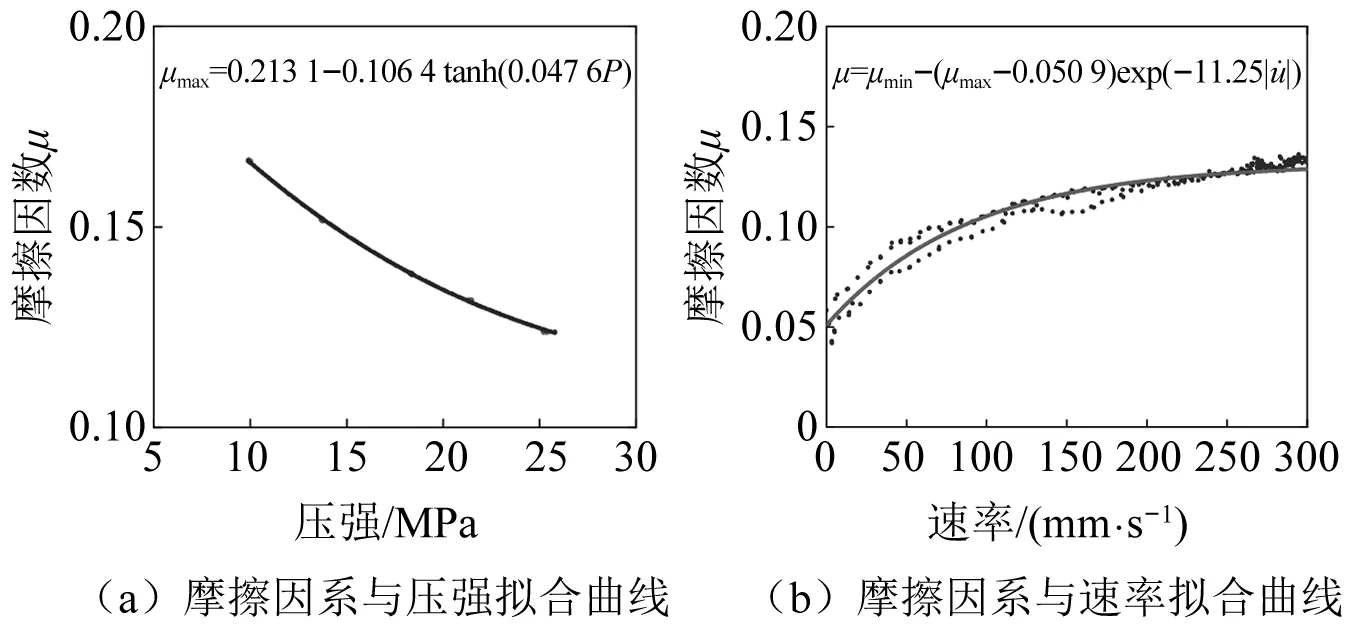
图8 PTFE材料考虑压强与滑动速率下摩擦因数模型Fig.8 Friction coefficient model of PTFE material considering pressure and sliding rate
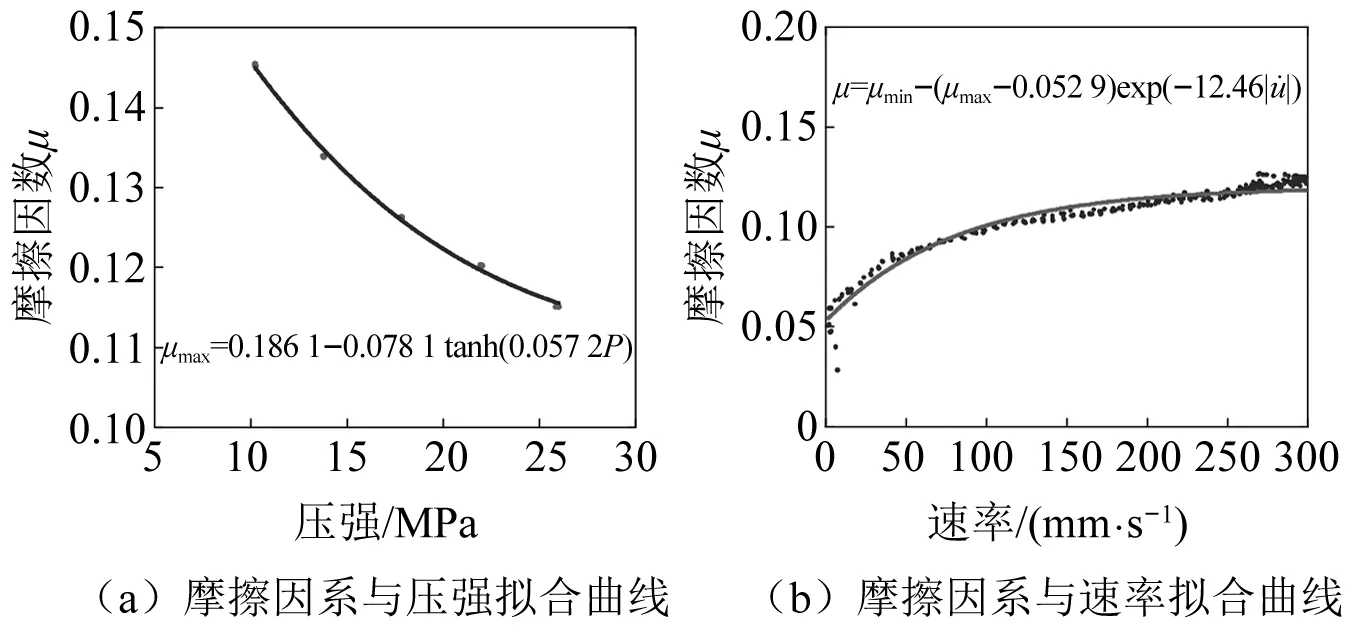
图9 PET材料考虑压强与滑动速率下摩擦因数模型Fig.9 PET material friction coefficient model considering pressure and sliding rate
3 摩擦因数仿真预测
受限于试验条件,上述测试最大摩擦速度为300 mm/s,FPS考虑PTFE与钢界面的摩擦效应研究和应用较多,此处以PTFE与钢摩擦为例,采用Materials Studio软件进行基于分子动力学的大速率摩擦因数预测分析。由于PTFE为高分子材料,选择了COMPASS力场。
3.1 PTFE-钢接触面微观模型
建立聚合度为10的PTFE分子链和尺寸为30 nm×30 nm×30 nm的钢模型,如图10(a)、图10(b)所示;随机建立PTFE无定型结构模型,尺度30 nm×30 nm×30 nm,如图10(c)所示。为了获得能量最低、结构合理的PTFE模型,进行几何优化与动力学平衡,选用COMPASS力场。具体步骤:①进行几何优化;②在300~600 K稳定范围进行15个循环的退火优化,使得PTFE模型得到充分驰豫;③分别在NVT与NPT系综,压强为0.1 GPa下进行动力学平衡,持续时间为2 000 ps。

图10 分子模型建立Fig.10 Molecular model established
3.2 摩擦模型
采用Build Layer建立摩擦模型如图11所示,固定钢原子层,然后对模型进行几何优化与动力学平衡,优化后取消对钢原子层的固定。施加预压荷载、速率进行步长为1 fs,时间1000 ps的模拟。

图11 摩擦模型Fig.11 Friction model
3.3 仿真模型验证
分析轨迹文件根据μ=f/N计算摩擦因数,摩擦因数时程曲线如图12所示。数据表明:加载一定时间后摩擦因数趋于稳定,对稳定状态下摩擦因数取均值计算得到摩擦因数。14 MPa,18 MPa与22 MPa下摩擦因数分别为0.145 5,0.138 0和0.113 0。可知随着竖向压强的增大摩擦因数逐渐变小,与试验相符。同时将模拟的摩擦因数与试验结果进行对比,如表7所示。由表7可知,误差介于12.3%~14.2%,摩擦因数的预测精度较高。

表7 摩擦因数模拟与试验对比Tab.7 Comparison of friction coefficient simulation and test

图12 PTFE与钢摩擦摩擦因数Fig.12 Friction coefficient between PTFE and steel
提取PTFE与钢摩擦过程中模型的状态图,如图13所示。
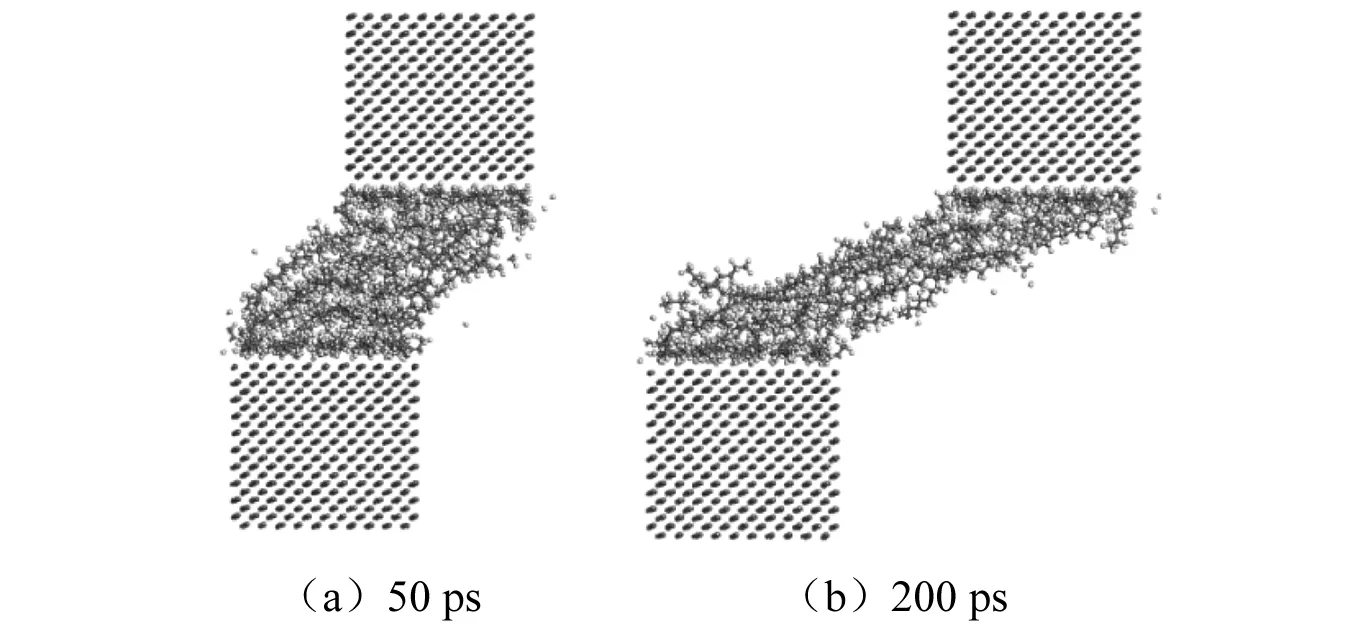
图13 摩擦过程轨迹图Fig.13 Trajectory diagram of friction process
3.4 大速率下摩擦因数预测
采用分子动力学对500 mm/s,700 mm/s滑动速率下摩擦因数进行预测,并结合试验数据采用指数函数进行拟合,拟合结果如图14所示。由图14可知,采用指数函数拟合显著性高,R2为0.938。因此可以采用该方法对试验的不足进行补充,并验明指数函数的适用性。
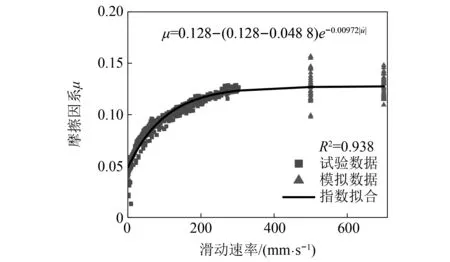
图14 指数函数拟合图Fig.14 Fitting of exponential function
4 结 论
本文通过实测与模拟为FPS的工程摩擦材料的特性进行了初步探究,结论如下:
(1) 随着滑动速率、压强的增大材料循环退化现象整体呈增大趋势;POM随着滑动速率增大,黏滞滑移越明显;POM与HDPE随着压强增大,黏结滑移减弱,其余材料均保持相对稳定。POM循环退化现象明显且离散程度大,不同滑动速率、压强下ks均值分别为0.937与0.911;方差分别为0.017 0与0.078 4;HDPE黏滞滑移现象明显,不同滑动速率、压强下kv均值分别为1.1624与1.147;PET的耐磨损性能最优,线磨损率为17.936 μm,PTFE和HDPE较差。
(2) 5种材料的摩擦因数随着瞬时滑动速率增大而增大,随着压强的增大而减小;压强对高速下摩擦因数影响大于低速下的影响;指数函数拟合摩擦因数与瞬时速率之关系的显著性优于对数函数;对于瞬时滑动速率、压强与摩擦因数关系,采用仅考虑压强对高速摩擦下摩擦因数影响的指数函数模型建模,拟合情况较好。
(3) 采用分子动力学预测PTFE与钢界面摩擦因数,低速误差介于12.3%~14.2%,结合试验与模拟结果,提出了较大速率下FPS摩擦PTFE的指数模型,验明了大速率效应下指数函数模型的适用性。

