多自由度混联Ⅰ型惯容减震系统地震响应分析

李创第, 王瑞勃, 江丽富, 葛新广

(1. 广西科技大学 土木建筑工程学院,广西 柳州 545006;2. 柳州工学院 土木建筑学院,广西 柳州 545616)

近年来,消能减震技术在建筑结构的抗风抗震中得到广泛应用[1-2],该技术通过在建筑结构的部分位置设置耗能装置,使其在外部激励作用下产生摩擦或剪切滞回变形等方式来消耗地震能量,从而达到降低结构动力反应的目的[3]。为此,众多学者[4-6]对已有耗能装置的改进及新型耗能装置的开发进行了大量研究。20世纪末,“inerter”(惯容)[7]作为一种新型被动控制装置被提出,惯容与传统耗能装置不同,它是两端点的惯性元件,所产生的惯性力可表示为同质量量纲一致的惯容系数与两端加速度的乘积。Ikago等[8]提出了以滚珠丝杠作为表观质量放大器的调谐黏性质量阻尼器(tuned viscous mass damper,TVMD),并首次将TVMD应用于单自由度结构中,研究发现,TVMD相对黏滞质量阻尼器(viscous mass damper,VMD)、黏滞阻尼器(viscous damper,VD)的减震效果更为显著。Wang等[9]研究了惯容在建筑悬架系统(即垂直基础隔振)中的性能优势,结果表明,惯容可以有效减小建筑系统的振动响应。在工程应用中,为进一步提高惯容的减震效果,常将惯容、弹簧以及耗能元件连接共同工作,三种元件连接所形成的动力系统称之为惯容减震系统。根据三种元件的连接方式将惯容减震系统分为串联型惯容系统、混联Ⅰ型惯容系统和混联Ⅱ型惯容系统[10-12]。串联型惯容系统由惯容、弹簧、耗能元件三者串联组成;混联Ⅰ型惯容系统由弹簧、耗能元件并联后再与惯容进行串联形成;混联Ⅱ型惯容系统由耗能元件、惯容并联后再与弹簧串联组成。Pan等[13]以结构随机振动响应的减缓率为设计指标,提出三种惯容减震系统的单自由度结构基于白噪声激励的设计方法,该方法在给定响应减缓率的情形下可快速获得单自由度惯容系统的关键参数,但所用白噪声激励与实际地震过程差异较大。Zhang等[14]发现并证明了阻尼增效现象的理论实质,基于阻尼增效方程提出了惯容减震系统通用的设计原理,运用实例对所提的方法及原理进行了验证。Lazar等[15]将混联Ⅰ型惯容系统应用到多层建筑结构,研究了惯容系统的减震性能,结果表明,惯容系统不仅可降低调谐质量、减小结构响应而且具有实现轻量化的优势,但在结构每层都设置惯容系统会使工程造价较高。潘超等[16]将结构减震性能、成本控制同时作为设计控制目标,分析了单自由度结构惯容系统结构响应解析式,在随机振动响应解析解的基础上,推导了简洁适用的参数设计公式。

由于地震过程具有随机性,国内外学者提出一系列随机激励模型拟合地震过程,如白噪声模型[17]、过滤白噪声模型[18-19]、胡聿贤模型[20]、李鸿晶模型[21]等。其中,李鸿晶模型不仅考虑了基岩的低频成分而且消减和控制了基岩的高频成分,该模型不仅可以描述地震的宽带特征亦可以描述窄带特性,是一种普适性强的随机激励模型。为深入研究地震激励对建筑结构的影响,需对结构基于随机地震模型下的响应进行分析,常用方法为时域法及频域法。时域法[22-23]以求解响应协方差为主,需求解激励的协方差;频域法[24-25]以建立响应和激励功率谱之间的代数关系为主。相比白噪声模型及过滤白噪声模型而言,李鸿晶模型以功率谱函数的形式存在,且功率谱函数较为复杂,运用时域法分析较为繁琐,频域法分析较容易。虚拟激励法[26]是频域法中典型的分析方法,该方法将平稳随机过程转化为简谐过程,简化了计算过程,但该方法在求解谱矩时尚需相当繁复的数值积分。针对以上不足,Ge等[27]在此基础上,提出了谱矩简明封闭解的计算方法,该方法通过求解响应功率谱的二次分解式(圆频率和模态复特征值平方和倒数的线性组合形式)将谱矩转化为模态参数与激励参数的线性组合,消除了复杂的积分运算且提高了计算精度。

目前针对惯容系统的研究多数基于单自由度结构展开,在多自由度结构中的应用及具体布置方案的研究较少。针对这一问题,本文运用文献[28]所提出的计算方法,分析混联Ⅰ型惯容系统在多自由度结构中的地震动响应,同时从性能和经济性角度出发,对惯容系统在多自由度中的布置方案进行研究。首先,求解多自由度结构部分层设置混联Ⅰ型惯容系统基于随机激励下的运动方程,并依据惯容系统的计算简图推导其微分型本构关系。基于此,重构运动方程,并运用复模态理论及虚拟激励法求解结构绝对位移、层间位移、层间位移角等系列响应的统一解。其次,对结构系列响应功率谱进行了二次分解,获得响应0～2阶谱矩的简明封闭解。最后,在响应谱矩封闭解的基础上,通过数值算例对比验证了所求谱矩的正确性;分析了复振型个数对结构响应谱矩计算精度的影响;确定并验证了惯容系统布置方案的有效性。

1 重构运动方程

在n层结构的部分层设置混联Ⅰ型惯容系统共l个(1≤l≤n)构成耗能结构,计算简图如图1所示。

图1 耗能结构计算简图Fig.1 Schematic diagram of the energy-consuming structure

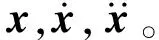
(1)

当结构第1层设置第1个混联Ⅰ型惯容系统时,计算简图如图2(a)所示;当结构第i层(当i>1)设置第h个(1≤h≤l)混联Ⅰ型惯容系统时,计算简图如图2(b)所示。由图2(a)和图2(b)可知,存在以下力学关系

图2 混联Ⅰ型惯容系统的布置简图Fig.2 Diagram of the arrangement of series-parallel layout Ⅰ inerter system

(2)

(3)

由式(2)、式(3)可知,所设l个惯容系统的力学关系为

(4)

(5)

联立式(4)、式(5),可得惯容系统与结构之间的微分型本构关系为

(6)

引入状态变量X,联立式(1)、式(4)～式(6)得到状态方程为

(7)

(8)

式中:α=[-MIo4o5o4]T,“T”为转置矩阵;o1为n×n阶元素为零的矩阵;o2为n×l阶元素为零的矩阵;o3为l×l阶元素为零的矩阵;o4为l×1阶元素为零的矩阵;o5为n×1阶元素为零的矩阵;M0,K0分别为

2 结构系列响应的统一解

2.1 复模态解耦

运用复模态法对式(8)进行解耦,式(8)中存在复特征值矩阵p及左、右特征向量V,U,满足

p=(VTM0U)-1VTK0U

(9)

引入复模态变换

X=Uz

(10)

式中,z为模态广义变量。

联立式(8)～式(10)可得

(11)

式中,η=VTα/(VTM0U)。

式(11)的分量形式为

(12)

式中:zk为响应分量;pk为复特征值;ηk为模态强度系数。

由虚拟激励法获得响应分量zk(ω)的频域解为

(13)

2.2 响应的频域统一解

联立式(7)、式(8)、式(13),获得结构第i层绝对位移和绝对速度的频域解分别为

(14)

(15)

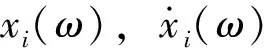
结构第i层的层间位移和层间速度频域解分别为

(16)

(17)

结构第i层的层间剪力为

(18)

(19)

结构第i层的层间位移角为

(20)

(21)

由式(14)～式(21)可知,结构系列响应的频域解可统一表示为

(22)

式中:Y(ω)为结构分量zk(ω)的频域统一解;κk为响应分量的模态系数,具体值由式(14)～式(21)确定。

3 响应功率谱及谱矩计算

3.1 结构系列响应功率谱的二次分解式

根据虚拟激励法,结构系列响应功率谱为

(23)

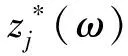
将式(13)代入式(23)可得

(24)

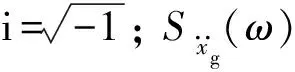
频率响应特征值函数HY(ω)的具体表达式为

(25)

(26)

式中:S0为谱强度系数;ωg,ξg分别为岩土层的特征频率和阻尼比;ωs,ωh分别为基岩扰动下的低频以及高频控制参数。

为便于求解结构响应谱矩,将式(26)进行简化,得到李鸿晶谱二次分解形式为

(27)

其中,

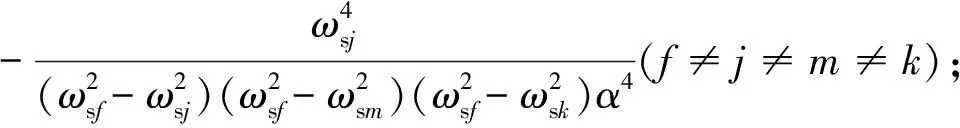
Δ1=-1-4iωsα; Δ2=-1+4iωsα。

根据代数运算将式(25)化简为

(28)

将式(27)、式(28)代入式(24),获得结构系列响应功率谱SY(ω)的二次分解式

(29)

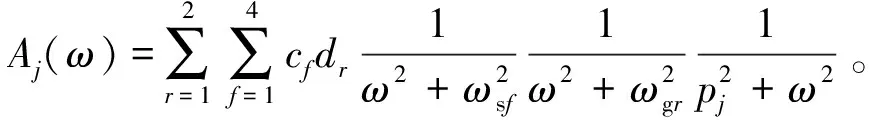
经上文分析可知,SY(ω)为响应分量对应的模态系数κk、复特征值pk、模态强度系数ηk、模态响应功率谱Aj(ω)的线性组合。

3.2 结构响应谱矩的封闭解

随机振动理论定义谱矩为

(30)

将SY(ω)的表达式(29)代入式(30),令q=0,q=1得到0阶、1阶谱矩,具体表达式为

(31)

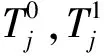
(32)

(33)

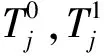
由于2阶谱矩是位移变化率的0阶谱矩,可有位移0阶谱矩进行表示,具体表达式为

(34)

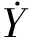
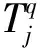
4 算例分析

一栋18层的混凝土结构,抗震设防烈度为8度,场地类别为Ⅱ类场地,场地土为中等土。1层为门厅和服务中心,2～3层用于养育托管管理配套等功能,其余楼层用于住宅。1层层高4.5 m,2～3层层高4 m,4～18层层高3 m;1层质量m1=6.5×105kg,2～3层质量m2=m3=4.9×105kg,4～18层质量为3×105kg;1层抗侧刚度k1=3×108N/m,2～3层的抗侧刚度k2=k3=2.15×108N/m,4～18层抗侧刚度为1.63×108N/m;结构阻尼比ς为0.05,主体结构的阻尼依据Rayleigh阻尼分析,即C=aM+bK,其中a,b为Rayleigh阻尼常数。

式中,ω1和ω2分别为结构的第一自振频率和第二自振频率,ω1=2.079 7 rad/s,ω2=6.105 5 rad/s。

混联Ⅰ型惯容系统的主要参数依据式(35)～式(37)确定

μ=md/m

(35)

κ=kd/k

(36)

(37)

式中:μ,κ,ξ分别为惯容系统的惯质比、刚度比以及名义阻尼比;md,cd,kd分别为惯容系统的惯容系数、阻尼系数、刚度系数;m,c,k分别为主体结构的质量、阻尼、刚度;ω0为结构的自振圆频率。

为同时满足结构的减震性能和成本要求,需合理拟合惯容减震系统的参数。潘超等研究了单自由度结构中惯容系统同时满足成本和性能的参数设计方法,利用所提公式及设计流程确定了混联Ⅰ型惯容系统满足成本和性能的优化参数值。由于多自由度惯容系统的性能-成本参数优化文献较少,故本文选取潘超等研究中的表1(混联Ⅰ型惯容系统的主要设计参数值),以目标阻尼比为0.04确定μ=0.085 1,κ=0.041 7,ξ=0.020 9。

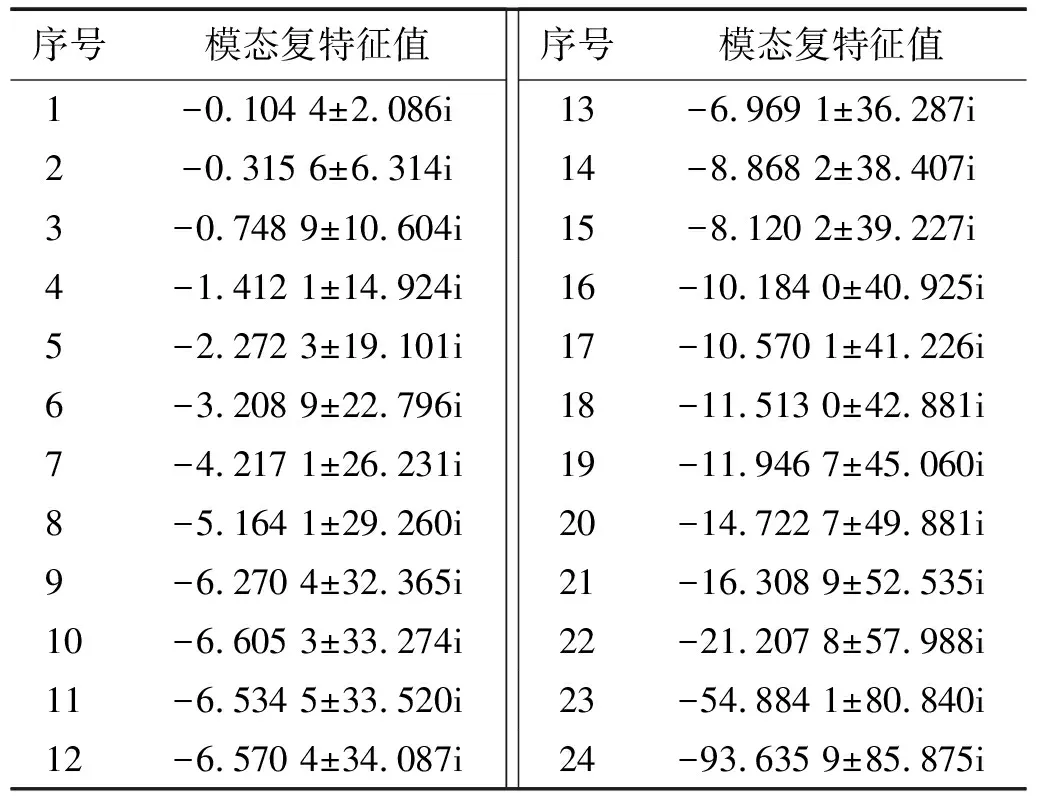
表1 结构响应模态复特征值Tab.1 Modal complex eigenvalues of response of the structure

通过式(35)～式(37)求得md=2.553×104kg,kd=6.797 1×104N/m,cd=2.923×104N·s/m。

4.1 封闭解的正确性验证

以1层、2层、4层、8层、14层、16层设置惯容系统为例,验证本文所求耗能结构响应谱矩封闭解式(31)～式(34)的正确性。由于虚拟激励法是结构随机响应分析中典型的计算方法,故将本文方法所得谱矩与虚拟激励法所得结果进行对比验证。

由附录A中式(A.9)可知,虚拟激励法求解响应谱矩需要对响应功率谱Sx(ω)在[0,∞]内进行积分运算,为获得稳定且精确的谱矩值,经试算积分区间取[0,500]rad/s,积分步长Δω依次取2.0 rad/s,1.0 rad/s,0.5 rad/s,0.1 rad/s。本文方法与虚拟激励法在4种不同积分步长下的谱矩对比,如图3所示。

图3 响应谱矩对比Fig.3 Comparison of response spectral moments

由图3可知,本文方法直接获得结构系列响应的谱矩,所得结果唯一、计算精确较高。虚拟激励法所求谱矩的精确度受积分步长取值的影响较大。当积分步长Δω≥1.0 rad/s时,各楼层谱矩的误差较大;当Δω≤0.5 rad/s时,各楼层的谱矩值逐渐趋于稳定,最终越来越接近本文方法所求结果;且当Δω=0.1 rad/s时,两种方法所得结果误差率小于3%。经上述分析可知,本文方法所求多自由度混联Ⅰ型惯容系统系列响应谱矩的封闭解正确有效,在推导过程中不仅简化了计算过程而且提高了计算精度。

4.2 复振型个数对结构响应精度的影响

由结构动力学可知,多自由度实模态分析中前若干振型对结构动力响应的影响显著,而其他高阶振型的影响较小可忽略不计。本文方法所求的振动特征值和振型为复参数,一对复共轭振动特征值和振型由欧拉变换可转化为一个实特征值和实振型。为满足结构动力响应的精度要求,并进一步提高本文方法的计算效率,将分析复振型对结构响应精度的影响。

由式(31)可知,本文所求谱矩值是复振动特征值与其他相关参数的线性组合。将以结构1层、2层、4层、8层、14层、16层设惯容系统为例,分析不同复振型下的响应值。表1为结构响应的模态复特征值pk,按照从小到大进行排序,将pk代入式(13),并依据式(14)～式(21)得到绝对位移、绝对速度等响应值,具体结果如图4所示。

图4 复振型对响应精度的影响Fig.4 Effect of mode shape on response calculation

由图4可知,只考虑1阶复振型时,所得位移、速度、层间位移角及层间剪力(所有楼层取平均值)依次占全振型的88.3%,78.0%,68.6%,60.0%;考虑前2阶复振型所得以上方差平均依次占全振型的98.9%,93.2%,89.9%,88.6%;考虑前3阶复振型所得以上响应方差平均依次占全振型的100.0%,98.5%,97.4%,96.2%。由此得出,复振型个数对结构位移的影响不明显,但对结构的层间位移角等响应影响较为突出,且对剪力的影响最大。高阶复振型对于较低楼层的动力响应影响较小,且前3阶复振型贡献率都超过95%。故在结构响应分析过程中,为保证计算精度、减少计算量、提高计算效率可只考虑前3阶复振型。

在考虑前3阶复振型的情形下,本文方法求解动力响应方差所用时间为0.094 8 s,运用传统方法计算所需时间为15.47 s,即考虑前3阶复振型具有较高的计算效率。

4.3 惯容系统布置方案的研究

在结构设计中,层间位移及层间位移角决定了结构内力和附属结构的安全。当层间位移或层间位移角过大时,可能导致结构的开裂或损坏,从而影响结构稳定性和舒适度。为满足结构的抗震性能和经济要求,以减小结构的层间位移或层间位移角为目标,分析惯容系统的布置方案。依据式(16)、式(17)、式(20)、式(21)对无控结构的层间位移、层间位移角进行了计算,具体结果如图5所示。

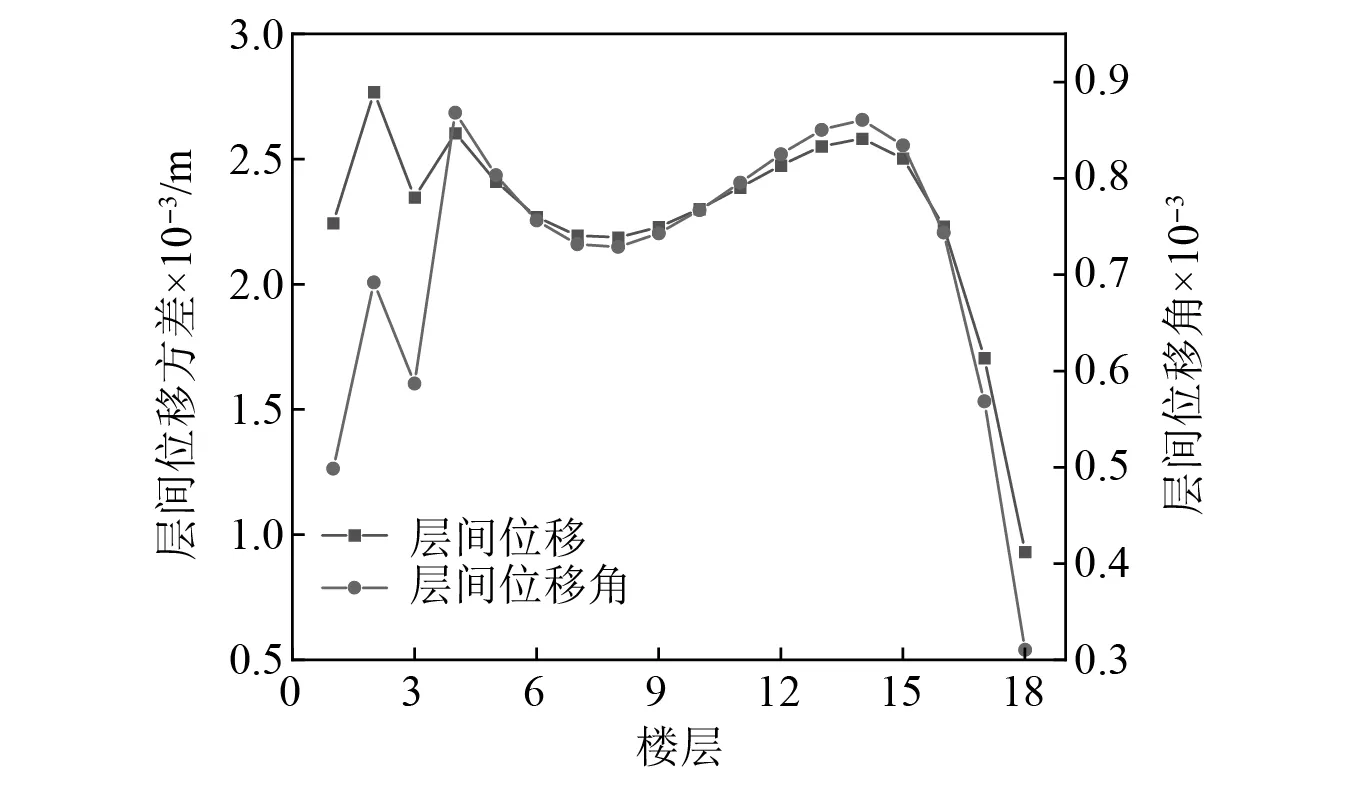
图5 无控结构的层间位移及层间位移角Fig.5 Interstory displacement and Interstory displacement angle of uncontrolled structure

由图5可知,在2层、4层、14层结构的层间位移、层间位移角同时出现峰值,此时对结构性能极为不利。依据层间位移、层间位移角峰值所在楼层,分别考虑其上、下层确定惯容系统在多自由度结构中的布置方案。具体方案1为1层、2层、4层、14层设置惯容系统;方案2为1层、2层、3层、4层、13层、14层、15层设置惯容系统;方案3为每层都设惯容系统。

依据式(14)～式(21)、式(31)～式(33)对各方案的位移、层间位移、层间位移角及层间剪力进行了对比计算,具体结果如图6～图9所示。

图6 布置方案的层间位移角对比Fig.6 Comparison of interlayer displacement angles of each program

图7 各布置方案的层间剪力对比Fig.7 Comparison of interstory shear force for each program

图8 各布置方案的绝对位移0～2阶谱矩对比Fig.8 Comparison of absolute displacement 0-2nd spectral moments of each program

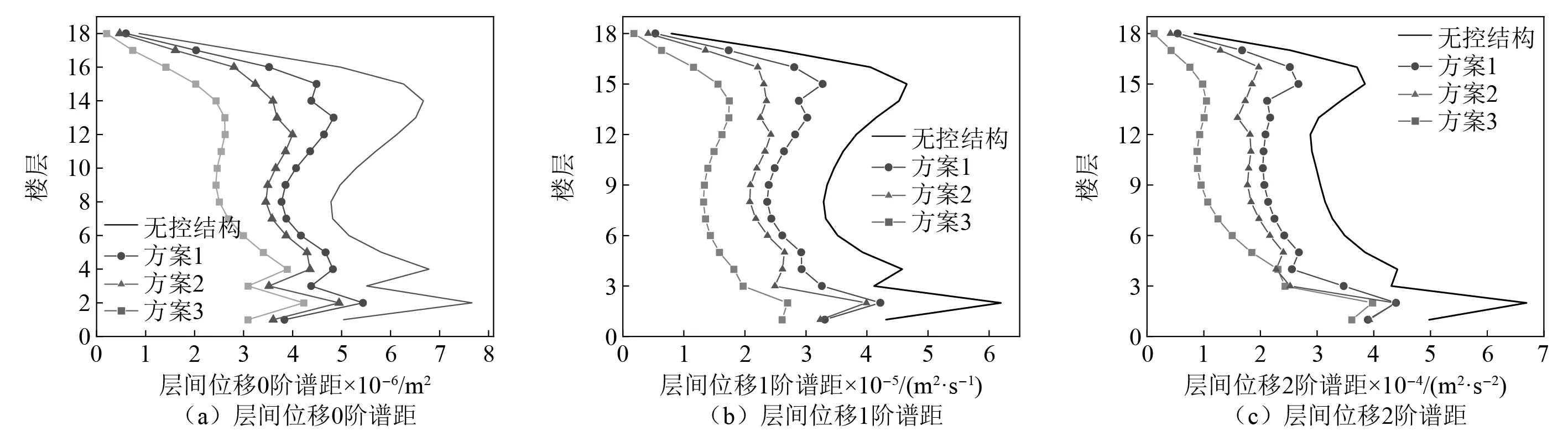
图9 各布置方案的层间位移0～2阶谱矩对比Fig.9 Comparison of 0-2nd spectral moments of inter-story displacement of each program

由图6～图9可知,方案3结构每层都设置惯容系统的减震效果最为明显,当结构中所设的惯容系统数量足够多时,结构的性能总能达到抗震设计要求,但这种做法从经济角度考虑是不可取的。

为更准确分析三种方案的可行性,对各方案在层间位移、层间位移角出现峰值楼层(2层、4层、14层)的减震效果进行分析,具体结果如表2所示。由表2可知:方案1对绝对位移、绝对速度、层间剪力、层间位移角、层间位移的最大减震率分别为27.3%,28.5%,34.3%,18.9%,30.9%;方案2对上述系列响应的最大减震率分别为33%,36.5%,48.3%,31.9%,46%。

表2 各布置方案的减震效果分析Tab.2 Analysis of vibration damping effect of each program 单位:%

经上述分析可知:方案3的减震效果最好,但所需成本较高;方案2的减震效果较方案1更加明显,且平均减震率在35%以上,能够有效降低结构层间位移和层间位移角。

5 结 论

本文将混联Ⅰ型惯容系统应用于多自由度结构的消能减震中,运用功率谱二次分解法给出了结构系列响应谱矩的封闭解,在结构响应0～2阶谱矩封闭解的基础上,对惯容系统在多自由度结构中的布置方案进行研究。为减小计算量、提高计算效率,本文分析了不同复振型对高层结构响应计算精度的影响。所得结论有:

(1) 本文在n层结构中设置l(1≤l≤n)个混联Ⅰ型惯容系统,将位移、速度、层间位移角等响应的0～2阶谱矩简化为模态谱矩、复特征值及其他参数的线性组合,运用数值算例验证了本文方法所求的谱矩正确适用。

(2) 获得多自由度结构混联Ⅰ型惯容系统的位移、速度等系列响应的频域解和0～2阶谱矩,对分析实际工程中结构动力可靠度如超过结构性能要求界限的平均率,首次破坏的时间及频率分布等具有一定的工程意义。

(3) 高阶复振型对位移的影响较不明显,但对速度、层间位移角、层间剪力等响应的影响较为显著。为准确分析和预测结构的抗震性能,高阶复振型的影响不能忽略。前3阶复振型对各响应的影响都在95%以上,故为简化计算量,提高计算效率建议考虑前3阶复振型。

(4) 本文在结构响应0～2阶谱矩封闭解的基础上,确定了惯容系统的布置方案。研究发现方案3减震效果最好,但整体造价较高;方案2相对方案1的减震效果较为显著,有效降低了层间位移和层间位移角,且该方案相对方案3降低了工程造价。为满足结构性能和经济要求,建议将惯容系统以方案2进行布置。

附录A:耗能结构响应谱矩的虚拟激励法

对式(1)、式(4)、式(5)进行傅里叶变换

(A.1)

(A.2)

(A.3)

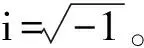
由式(A.2)、式(A.3)得到

(A.4)

(A.5)

把式(A.4)和式(A.5)代入式(A.2)则

(A.6)

将式(A.6)代入式(A.1)得到结构绝对位移为

(A.7)

式中,Hx(ω)=-Mω2+iωC+K+I1DFS(ω)。

结构层间位移为

Δxi(ω)=xi(ω)-xi-1(ω),i=2～n

(A.8)

式中, Δx1(ω)=x1(ω)。

结构层间剪力为

V1(ω)=k1x1(ω)

(A.9)

Vi(ω)=ki[xi(ω)-xi-1(ω)],i=2～n

(A.10)

结构层间位移角为

(A.11)

(A.12)

结构位移的功率谱为

(A.13)

速度的功率谱为

(A.14)

层间剪力、层间位移角等响应可依据位移及速度的功率谱进行求解。

将(A.7)代入谱矩计算公式,得到绝对位移0～2阶谱矩为

(A.15)