基于声发射及WST-CNN协同的滑动轴承润滑状态识别
卢绪祥, 刘顺顺, 陈向民, 张 亢
(长沙理工大学 能源与动力工程学院,长沙 410114)
滑动轴承是汽轮机组等大型旋转机械的核心部件,由于运行负载高、工作环境恶劣,长时间运行易导致润滑状态恶化,进而引发一系列不良反应,诸如碰摩、咬黏、腐蚀、裂纹等等,最终导致油膜失稳,破坏正常润滑状态,引起重大安全事故,因而对滑动轴承润滑状态进行有效监测及预警具有重要意义[1]。
对滑动轴承进行状态监测的常用信号有:振动信号、声发射信号、轴心轨迹、光铁谱分析等。振动分析是工业中最常用的监测技术之一。具有信号丰富、传感器安装方便等优点,但信号的主要能量集中分布在1 500 Hz以下低频区域,而干扰信号频率也多为低频信号,故将有效信号完全分离比较困难。而声发射检测具有较宽的频率范围,获取的信息量更大,利用高频段信号进行故障诊断,可有效排除其他低频干扰信号。
近年来,机器学习与深度学习在滑动轴承的故障诊断中得以广泛应用。Babu等[2]使用小波变换对信号进行分解,结合人工神经网络对滑动轴承进行多种工况故障诊断,分类准确率达到了85.7%。为进一步提高识别精度,Babu等[3]对振动信号提取多种特征,使用自编码器实现深度神经网络并对数据特征进行训练,该方法在相应试验数据下可实现100%的高识别率。然而,若故障数增加,会导致故障类型出现重叠,且滑动轴承运行环境噪声污染严重,则会导致机器学习的准确性降低。Tang等[4]提出一种基于统计滤波和叠加自编码器的分步智能诊断方法,采用去噪信号作为输入,能更有效地自动学习区分关键特征。König等[5]将声发射技术应用于滑动轴承试验台,采用基于卷积神经网络(convolutional neural network, CNN)的深度学习方法,对磨损失效模式进行监测和分类,达到了较高的精度。Luo等[6]将卷积神经网络进行简化,使其在保证诊断准确性的同时,提高了计算效率。在滑动轴承的故障识别中,效率与精度同样重要,但在磨合和润滑不充分的情况下,两者有时会被误判,降低整体分类的准确性。因此,本文针对某310 MW汽轮发电机组滑动轴承现场试验所得的声发射信号,采用小波散射对声发射信号进行特征提取,结合简化卷积神经网络对滑动轴承进行早期故障诊断,该方法能在保留有效特征信息的情况下显著减小特征尺寸,提高诊断精度和效率。
1 滑动轴承的声发射机理
声发射是指材料在外载荷或内力作用下以弹性波的形式释放应变能的现象。在滑动轴承运行时,轴瓦、轴颈之间被一层润滑油膜所隔开,声发射主要源自内部轴瓦、油液、轴颈之间的摩擦。高速旋转状态下,滑动轴承内部轴瓦与轴颈与油膜相互摩擦挤压,应力分布不稳定,当所受应力达到一定程度时,金属材料会通过晶格间的位错、滑移、龟裂等形式向外释放弹性波。声发射信号的强弱与滑动轴承油膜厚度之间具有较强的联系性,一般情况下,油膜厚度大小与声发射信号强弱之间呈正相关,但当油膜厚度低于混合润滑状态的厚度时,声发射信号强度会急剧增大[7]。
声发射信号信噪比高,与传统的检测油温、轴温等方法相比,声发射响应时间短,能更快地反映故障;另一方面,声发射传感器安装方便,与检测油膜厚度和轴心轨迹等方法相较,更适用于对滑动轴承进行在线监测;与光铁谱分析方法相比,声发射具有能够及时指示且能够定位故障的特点[8]。
现场试验的滑动轴承为某310 MW发电机组(轴系结构如图1所示)的低压缸后轴承,也即机组的4号支持轴承。该轴承为椭圆瓦结构,轴承体由上半和下半组成,水平对分,采用两支定位销来确保装配时的两半轴承体精准对中。轴承的基本参数包括:轴承半径R=0.241 3 m,长径比1/d=1,宽度L=0.482 m,轴承半径间隙C=0.48×10-3m,轴承承载力N1=3.36×104N,粗糙度σ=3.2×10-6m。由于该轴承负荷大,轴承座刚度差等原因,经常出现瓦温高、瓦振较大及磨损等情况,因此机组小修时经常对4号轴承进行检查。
如图2所示,本次试验利用耦合剂将声发射传感器直接粘贴至轴承座表面,试验时该传感器的采样频率为3 MHz,详细试验过程见文献[9]。

图2 现场安装的声发射传感器Fig.2 Installation of acoustic emission sensor
本次试验过程中,在转速2 040 r/min阶段进行了长时间暖机,期间凝汽器压力有一降低过程,导致机组轴承上抬,4号轴承的润滑状态开始恶化,随后声发射信号突然降低并维持了一段时间,为便于后续分析,将这段时间内的滑动轴承润滑状态划分为混合润滑状态;最后声发射信号又出现突增,机组油温、瓦温超标打闸停机,将这段时间内的滑动轴承润滑状态归为干摩擦状态。停机后检查发现4号轴承发生了严重磨损,轴瓦及轴颈磨损情况如图3所示。

图3 磨损的4号轴瓦及轴颈Fig.3 Photos of worn bearing bush and journal
如图4所示为现场获取的声发射信号时域波形图,从上到下依次为正常润滑、混合润滑、干摩擦三种状态信号的时域波形图。
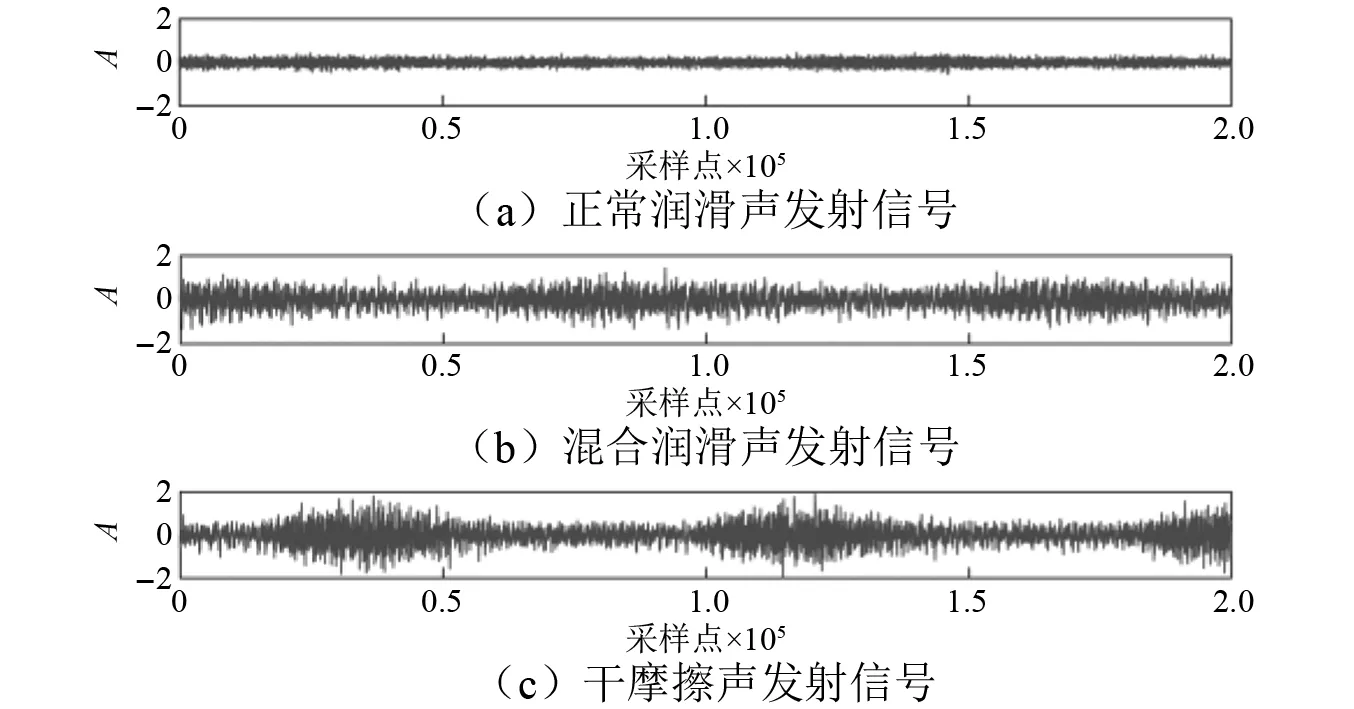
图4 滑动轴承三种润滑状态下声发射信号时域波形图Fig.4 Time domain waveform of acoustic emission signal under three lubricating conditions
从图4看出,滑动轴承从正常润滑到混合润滑再到干摩擦变化的过程中,声发射信号的幅值有明显增大,信号波动性也更强。正常润滑状态的幅值约为[-0.5 0.5],混合润滑状态的幅值约为[-1 1],干摩擦状态的幅值约为[-2 2],以上体现出声发射信号检测灵敏的特点。不过由于滑动轴承工作环境恶劣,声发射信号极易受周围环境噪声干扰,仅从时域图获取的信息有限,即使同一状态下的声发射信号特征也并不明显。因而,提取有效的特征值仍是声发射信号故障诊断领域的研究重点[10]。
继续从频域、时频域分析滑动轴承声发射信号,图5、图6分别显示的是三种润滑状态下,声发射信号平滑后的持久频谱图以及尺度图。
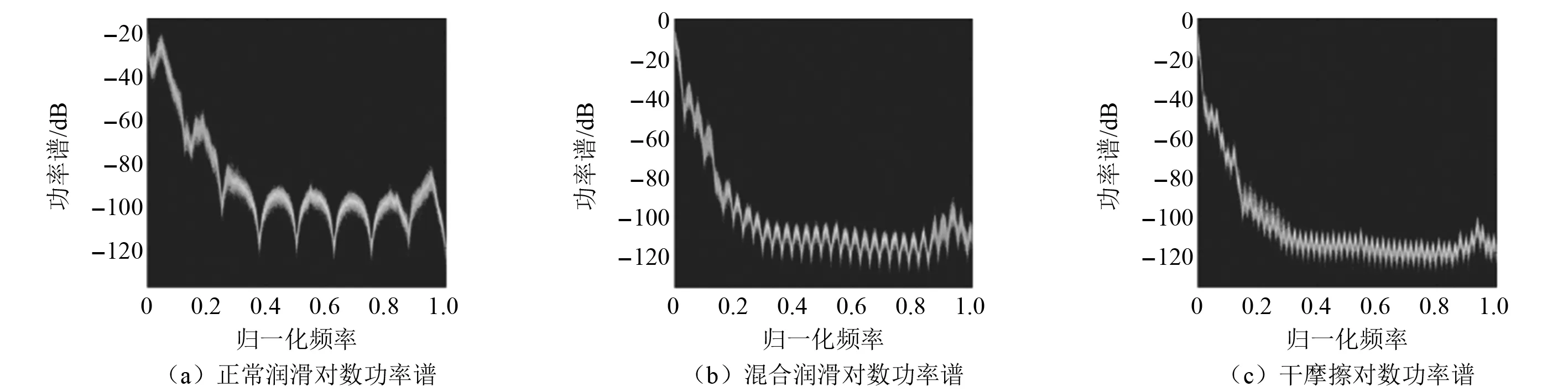
图5 三种润滑状态下声发射信号平滑后的对数功率谱图Fig.5 Log power spectrum of acoustic emission signal after smoothing under three lubricating conditions

图6 三种润滑状态下声发射信号尺度图Fig.6 Scale figure of acoustic emission signal under three lubricating conditions
从图5可以看出,滑动轴承三种润滑状态的声发射信号经平滑后的对数功率谱图有着直观的区别:正常润滑信号的功率谱参数随归一化频率的增大而出现大范围波动,波动周期较长;混合润滑状态信号的功率谱参数随归一化频率的增加而出现较为快速的波动;干摩擦状态信号的功率谱参数随归一化频率的增加出现急剧波动,波形已接近锯齿形。
从图6可以看出,滑动轴承三种润滑状态的声发射信号的尺度图也有明显差异:正常润滑状态下声发射信号的能量较低且平稳;混合润滑状态下声发射信号的能量分布较为散乱,主要能量间断性分布在归一化频率值0.001周围;干摩擦状态下声发射信号的能量持续凸显,在归一化频率值0.001及其上、下位置呈条带状分布。
2 小波散射变换
由于实际采集到的滑动轴承声发射信号会受到周围工作环境的噪声干扰,影响故障早期微弱信号的识别和分析。故需要一种兼具平移不变性和局部稳定性的信号特征分析提取方法。在本文中,采用小波散射变换(wavelet scattering transform, WST)来对滑动轴承声发射信号进行自动鲁棒特征提取。
WST是一种冗余的时频变换技术,在信号分类中具有显著优势[11],可以提取在声音、图像信号中的高分类精度特征。刘辉等[12]将小波散射技术应用到输电线路故障诊断中,对故障电流信号进行WST特征提取,并结合长短期记忆神经网络进行诊断,大幅提升了故障辨识准确率。Varun等[13]对现有的WST固定时频表示进行修改,使其可学习信号的时频表示,该方法在轴承和齿轮故障的诊断中表现优异,并且具有良好的迁移学习性能,能够很好的推广到故障诊断领域。
小波散射网络基于现有小波的固定时频表示,经修改可使其学习故障诊断的最佳特征。小波散射框架如图7所示。小波散射首先使用小波低通扫描滤波器φ对输入信号进行平均化操作,生成第0层散射系数;接着高通小波滤波器ψ对信号进行连续小波变换生成一组尺度图系数,将非线性算子(称为模数)应用于尺度图系数,对输出进行小波低通滤波器滤波,生成第一层散射系数;上一层的输出成为下一层操作的输入,重复相同过程继续获得第2层散射系数…简言之,WST可概括为对加入了非线性运算的小波特征进行卷积计算,以获得具有平移不变性和局部稳定性的小波特征[14],小波散射变换公式为

图7 小波散射框架Fig.7 Framework of wavelet scattering transform
SJ(n)f=|f·ψn(x)|·φJ
(1)
式中:ψ为高通滤波器;φ为低通滤波器;J为最大尺度;SJ(n)f为散射系数即小波散射特征。
由于每次迭代都需要占用更多算力,对于滑动轴承声发射信号而言,3层即可满足应用:第1层基本上执行平均操作,但丢失了信号的细节;第2层捕获细节,类似于尺度不变特征变换功能;第3层提供补充信息,可改善分类。图8所示的是三种状态下滑动轴承声发射信号的0阶、1阶、2阶散射分解系数,由各阶散射系数的数值可以看出,滑动轴承声发射信号的能量主要在1阶、2阶体现。

图8 滑动轴承三种润滑状态下散射系数分布图Fig.8 Scattering coefficient distribution diagram of sliding bearing under three lubricating conditions
通常对系数进行下采样以降低网络的计算复杂性,这些散射系数统称为散射特征,对散射特征进行2阶散射系数可视化分析,如图9所示,与1阶散射系数相比,由于散射分解次数的增加,低频部分的能量逐渐凸显,故障信号2阶散射系数的可视化特征具有明显的冲击性,可以有效区分干摩擦状态与混合润滑状态。
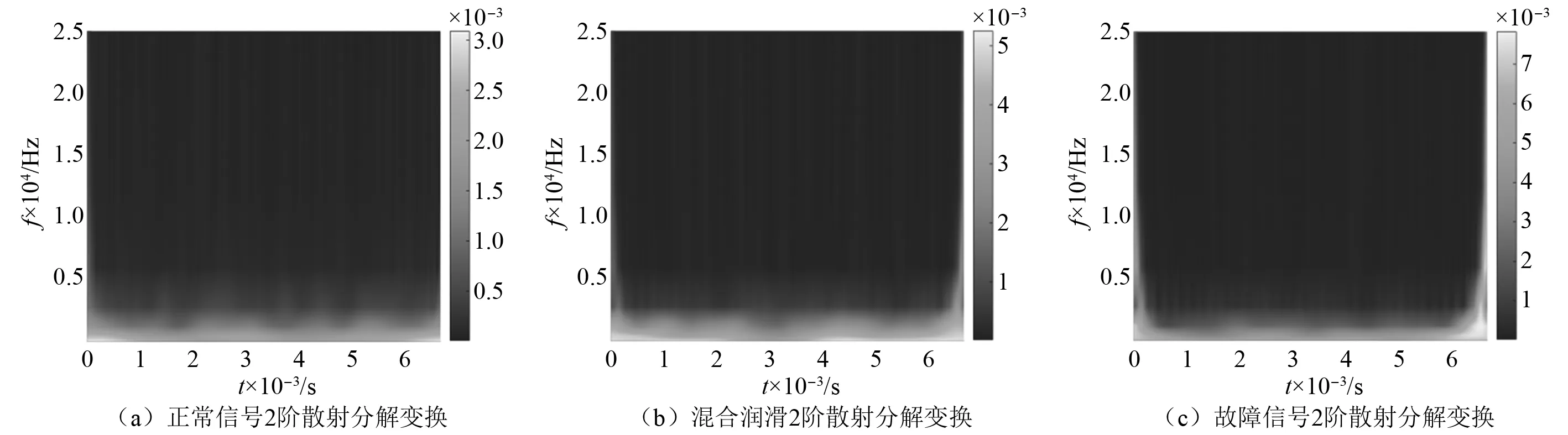
图9 滑动轴承三种润滑状态信号2阶散射变换时频谱Fig.9 Second order scattering transform time spectrum of sliding bearing under three lubricating conditions
在传统或者浅层的机器学习技术当中,通常需要一个手动的特征提取步骤,从图像等数据中学习有区别的信息。特征及分类器必须手动设计和选择。对数据进行小波散射变换,既可以实现对监测数据的降维,减少冗余信息,提高计算效率,又可以提取数据本质特征,并且可以提取隐式信号特征[15]。且通过上述分析可知,使用小波散射2阶系数可以有效观察滑动轴承三种润滑状态声发射信号的时频特征及能量分布。
图10所示为小波散射网络结构,小波散射网络被称为深度网络,因为它会执行构成深度网络的3个主要任务:卷积、非线性和池化。卷积由小波执行,模运算符用作非线性化,小波低通滤波器的滤波类似于池化。小波散射网络能够以较少的配置从时间序列和图像数据中获取低方差特征,在降维的同时捕获重要信息。以便在机器学习和深度学习中使用。小波散射网络在功能上等效于深度卷积网络,但不包含任何参数,适用于非密集型数据集,与卷积神经网络的区别主要在于,卷积神经网络的滤波器权重是习得的,而小波散射网络的滤波器权重是固定的。

图10 小波散射网络结构Fig.10 Structure of wavelet scattering network
通过计算机程序对已有数据进行分析,试验所取声发射信号采样率为3 MHz,信号总长度为200 000个采样点,选取了共1 200条事件信号,包含400条正常润滑信号、400条混合润滑信号及400条干摩擦信号。
由文献[16]可知当散射分解采样频率与时间不变尺度之积近似等于采样点总数N时,可得到最佳维数的特征矩阵。设定小波散射分解采样率为3 MHz,时不变尺度为0.000 6 s,小波变换次数为2,质量因子为8和1。同时加入散射路径优化机制,能够去除冗余特征,在保证准确率的同时提高运算效率,提升特征矩阵鲁棒性,经过进一步训练和测试,以得到最优的散射特征矩阵。图11为加入优化机制前后散射路径图。通过分析,加入散射路径优化机制后,减少了82条散射路径,特征矩阵的体积减小了32.54%。

图11 优化前后散射路径图对比Fig.11 Comparison before and after adding scattering path optimization mechanism
3 基于小波变换模极大值的碰摩检测
通过构造小波散射网络对数据进行变换,从测试数据中选择一个时间序列并对数据进行分类,对正常润滑、混合润滑状态、干摩擦状态三种信号运用小波变换模极大值技术,运行结果如图12所示。

图12 滑动轴承声发射信号的小波变换模极大值图Fig.12 Maximum value of wavelet transform modulus of acoustic emission signal of sliding bearing
小波变换模极大值是在对多尺度小波变换进行不规则抽样的基础上得到的,主要利用了小波变换对突变信号的敏感性以及小波变换在时域及频域良好的定位能力。小波变换模极大值线上的最大值通常出现在粗糙的尺度区域,极大值线上的最小值则出现在精细的尺度区域。由图12可知,正常信号的能量尺度最小且模极大值分布均匀,混合润滑信号的能量尺度较大,模极大值呈间歇性分布,而干摩擦状态的能量尺度最强,且模极大值分布比较密集且杂乱。图12(b)中,混合润滑状态信号在采样点617,1 077,1 400,1 788位置处有收敛到最细尺度的极大值线,通过收敛到最细尺度的极大值线可对突变信号实现奇异点定位。
绘制混合润滑状态信号样本的波形图,并标定采样点617,1 077,1 400,1 788处的位置如图13所示。基于混合润滑信号波形图的变更点分析进一步确认了小波变换模极大值分布的结论:采样点617,1 077,1 400,1 788处可能是混合润滑状态时出现碰摩的区域。
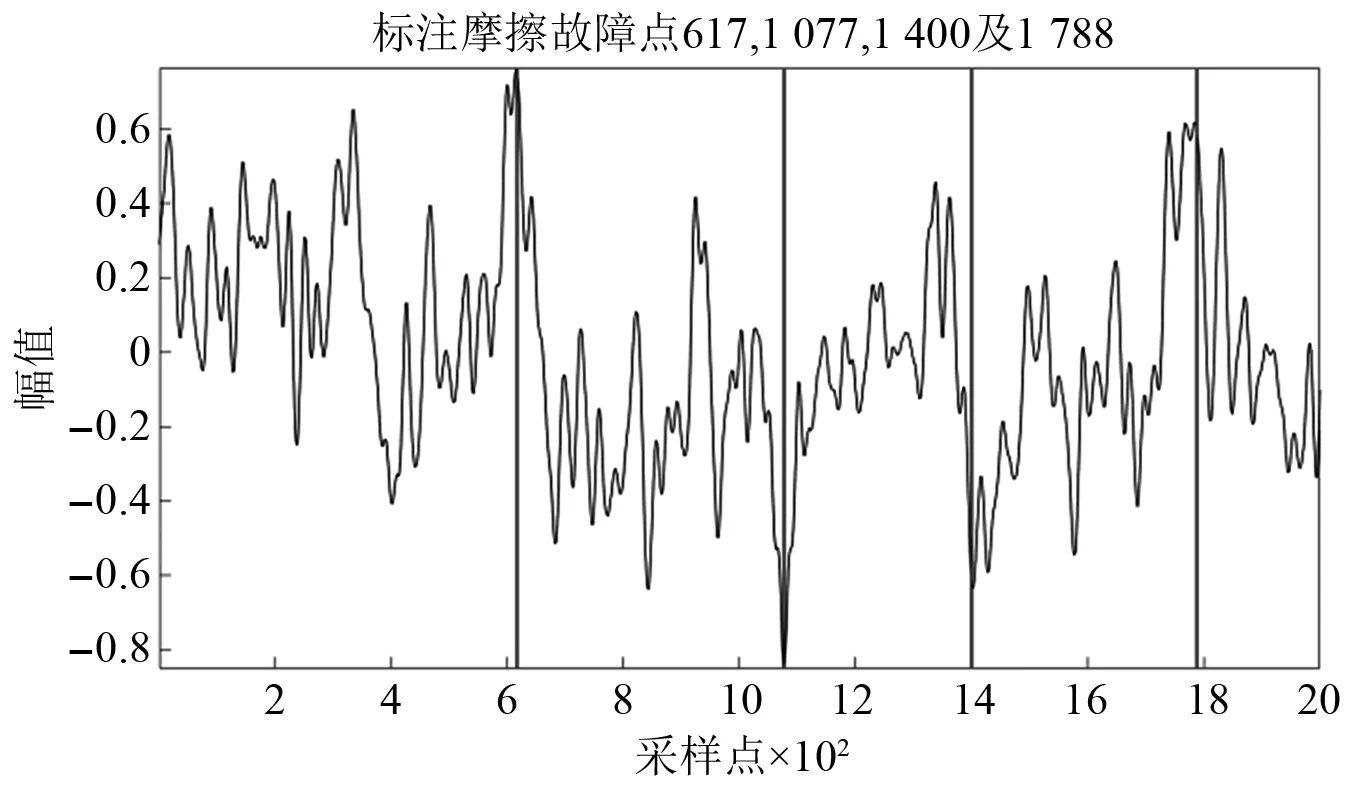
图13 混合润滑信号波形图Fig.13 Mixed lubrication signal waveform diagram
4 基于WST-CNN润滑状态识别
卷积神经网络通过模拟人脑视觉系统,交替采用卷积层和池化层,增强原始信号并对图像进行邻域间采样,在卷积层后进行批量归一化处理可增强模型的泛化能力并提高训练速度[17]。图14所示为卷积神经网络结构。
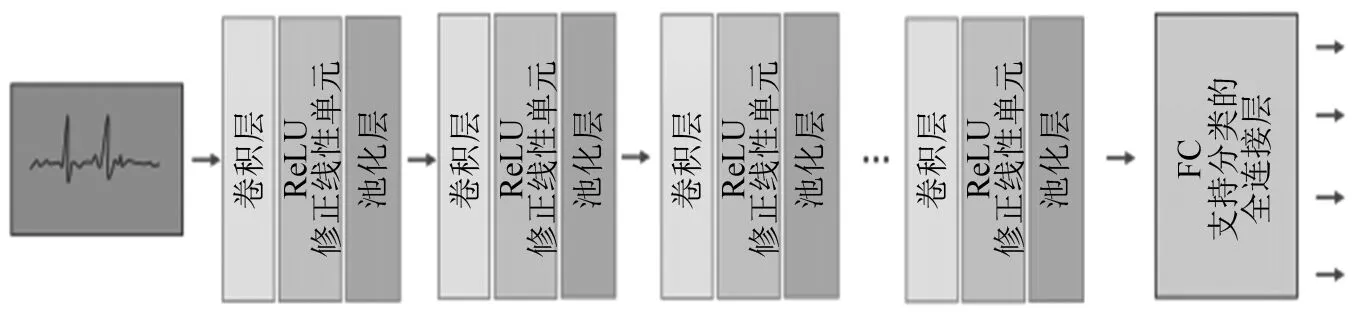
图14 深度卷积网络结构Fig.14 Deep convolutional network structure
将通过小波散射分解变换得到的最优特征矩阵数据集按照7∶3分为训练集和测试集,作为卷积神经网络的输入,用小波散射序列训练一个一维卷积神经网络,散射序列为32×63,其中63为时间步长,32为散射路径数。对卷积网络训练相关参数进行设置,经多次测试发现,与SGDM及Adam优化器相比,采用RMSProp优化器训练得到的网络效果最佳,较Adam优化器网络准确率平均高3.65%,较SGDM优化器网络准确率高1.81%,且具有更强的泛化能力。训练后返回网络和训练信息,图15所示为WST-CNN训练过程中准确度与损失信息。
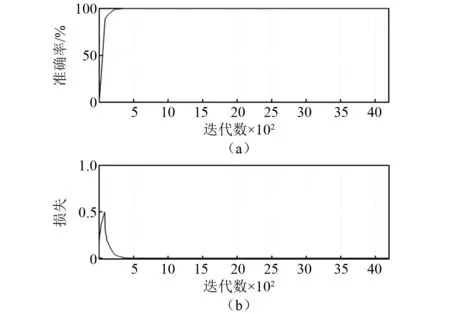
图15 WST-CNN训练精度与损失曲线Fig.15 Training accuracy and loss curve of the WST-CNN
将测试集的小波散射特征矩阵作为WST-CNN模型的测试输入,绘制混淆矩阵如图16所示。结果显示:整体准确率达到95.28%(平均值),其中正常润滑状态的信号识别率达到100.00%,混合润滑状态的识别率93.30%,干摩擦状态的信号识别率达到92.50%。

图16 滑动轴承润滑状态识别效果混淆矩阵Fig.16 Confusion matrix of lubrication state of sliding bearing
为对比验证该方法的有效性,使用同一滑动轴承声发射信号设置三组对照,分别为小波散射结合门循环单元(gate recurrent unit,GRU)循环神经网络(wavelet scattering transform-gate recurrent unit,WST-GRU)、数据增强的声发射信号结合GRU循环神经网络(data enhanced acoustic emission signal-gate recurrent unit,DEAES-GRU)、数据增强的声发射信号结合卷积神经网络(data enhanced acoustic emission signal-convolutional neural network,DEAES-CNN)。四种模型间的对比如表1所示。从表1可以看出,无论是预测准确性还是在模型的时效性上,WST-CNN都具有较为明显的优势。
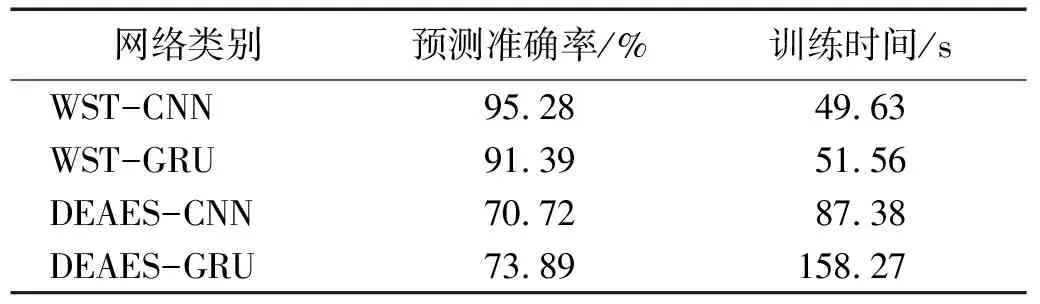
表1 不同模型效果对比Tab.1 Comparison of effects of different models
由此证明,基于WST-CNN的方法对滑动轴承声发射信号的智能识别准确率较高,并且能够高效、迅速地对滑动轴承润滑状态进行分类。
5 结 论
(1) 相较于振动信号检测,使用声发射技术对滑动轴承润滑状态进行检测具有灵敏度高、频率范围宽、信息量更大的优势。滑动轴承的润滑状态与声发射信号的强弱具有较强的联系性,采用小波散射技术对滑动轴承信号进行处理,可以提取出低方差特征矩阵,降低计算量的同时捕获重要信息。
(2) 小波散射网络设置简便,对提取的特征矩阵易于理解和解释,并且兼具平移不变性与局部稳定性,提取的特征矩阵也具有更强的鲁棒性。在实际应用中对小波散射网络的主要参数进行选择及比较,总结得到:在信号采样频率不变时,时不变尺度与采样频率之积越接近数据采样点数,所提取的特征矩阵区分度更高;对滑动轴承声发射信号使用3次小波散射分解变换即可满足使用,在保证网络有效性的同时提高程序运算效率。
(3) 使用小波变换模极大值技术可以对滑动轴承润滑状态进行有效区分并对发生碰摩的采样点进行诊断,通过在信号波形图中标注出现小波变换模极大值的点,能够进一步确认信号采样点中发生碰摩的区域。
(4) 对WST-CNN方法与WST-GRU及其他方法进行了比较,结果表明,优化后的小波散射网络能够有效提取声发射信号特征,结合优化后的卷积神经网络对特征矩阵进行智能识别,对滑动轴承润滑状态识别率可达到95%以上,能够高效精确地对滑动轴承润滑状态进行诊断。

