等离子体层嘶声波对辐射带电子投掷角散射系数的多维建模*

王敬之 马新† 项正2)‡ 顾旭东 焦鹿怀 雷良建 倪彬彬

1)(武汉大学电子信息学院,武汉 430072)

2)(中国科学院地质与地球物理研究所,地球与行星物理重点实验室,北京 100029)

等离子体层嘶声波(plasmaspheric hiss)是地球辐射带中一种常见的电磁波动.嘶声波可以通过波粒相互作用将辐射带电子散射进入损失锥进而沉降到中性大气,因此是导致辐射带电子损失的重要波动源.作为电子能量和投掷角的变化函数,嘶声波对辐射带电子的散射系数受到太阳风和地磁活动水平的显著影响,还强烈依赖于空间位置、背景磁场和等离子体密度分布.为了快速获取嘶声波对辐射带电子的投掷角散射系数以用于辐射带全球动态变化过程建模,本文利用FDC(full diffusion code)系统计算了嘶声波对辐射带电子的散射系数,建立了空间区域L=1.5—6、冷等离子体参数α*=3—30、电子能量1 keV—10 MeV、电子投掷角0°—90°范围内的四维散射系数矩阵数据库.基于该数据库,可通过线性插值快速得到不同L和α*参数下的嘶声波对辐射带电子的散射系数.通过对比FDC 计算的散射系数与线性插值的结果,验证了基于数据库线性插值得到散射系数的准确性,大部分误差位于10%以内.本文建立的嘶声波对辐射带电子的投掷角散射系数四维数据库和验证的线性插值方法,可以大幅降低获取嘶声波散射系数全球信息的时间,从而快速提升开展长时间辐射带时空变化模拟的计算效率,进而有望为开发地球辐射带动态预报模型提供有利条件.

1 引言

地球辐射带中充满了被地磁场捕获的高能粒子,这些高能粒子通量的变化是多种加速和损失机制相互竞争的动态平衡结果.多种波动类型可以导致地球辐射带电子的损失,例如静电电子回旋谐波(electronstatic electron cyclotron harmonic wave,ECH 波)[1,2]、哨声模合声波(wistler-mode chorus,Chorus 波)[3−8]、等离子体嘶声(hiss wave,Hiss 波)[9−12]、电磁离子回旋波(electro-magnetic ion cyclotron wave,EMIC 波)[13−21]和人工甚低频台站信号[22−27].其中,嘶声波是一种宽频带非相干哨声模电磁波,常在等离子体层内向日侧和羽流背日侧发生[28−32].嘶声波的激发原因可能是亚暴时高能电子注入形成的热不稳定性[33−35],也可能是哨声模合声波传播进入等离子体层演化形成[36−38].嘶声波对辐射带电子分布有非常重要的作用,是辐射带槽区形成的重要机制[39−42].根据范艾伦卫星2015 年磁平静期的观测发现,嘶声波对不同能级电子具有不同强度的散射效应,导致 “S” 型高能电子分布形成[43−45].Zhao等[46]通过卫星观测和数值模拟发现嘶声波能够导致电子反转能谱的形成.Ni等[47]通过数值模拟进行了详细的参数分析,揭示了嘶声波引起的反转电子能谱对背景磁场、等离子体密度和嘶声波频谱分布特性的依赖性.

之前的研究表明,在低L(磁力线在磁赤道处的地心距离,以地球半径RE为单位量化)区域可以观测到嘶声波散射高能电子进入损失锥,导致显著的电子沉降[48−50].基于准线性理论[9,39−42,51]的模拟结果表明由嘶声波引发的投掷角散射效应及所伴随的电子通量衰减与卫星观测结果基本吻合[52−54].嘶声波发生频率高,并且分布极广,由于卫星轨道的限制,单个观测事例很难满足辐射带建模的需要.为了量化嘶声波对辐射带电子的影响,需要花费大量时间去计算嘶声波对辐射带电子的散射系数.因此,能够快速得到嘶声波对辐射带电子的散射系数将大大提升辐射带建模效率.本研究建立了一个在偶极磁场下的以背景等离子体参数α*以及空间位置参数L为输入参数的嘶声波散射系数矩阵数据库,基于此数据库可以通过线性插值快速得到不同α*和L下嘶声波对辐射带电子的散射系数,为辐射带快速建模提供了有利条件.

2 模型和方法

本文基于FDC(full diffusion code)[13,55−57]计算嘶声波对辐射带电子的散射系数.输入参数主要包括:背景磁场强度、嘶声波的频谱分布、传播角分布、嘶声波的磁纬度覆盖范围、背景等离子体密度.

投掷角扩散系数Dαα[58]的具体计算公式如下:

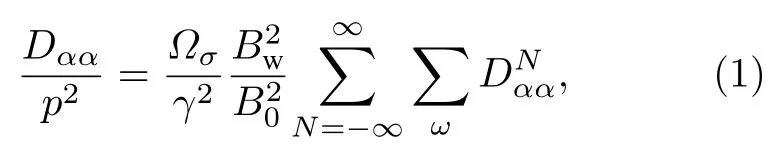
其中Bw为平均幅值,B0为背景磁场的强度,同时:

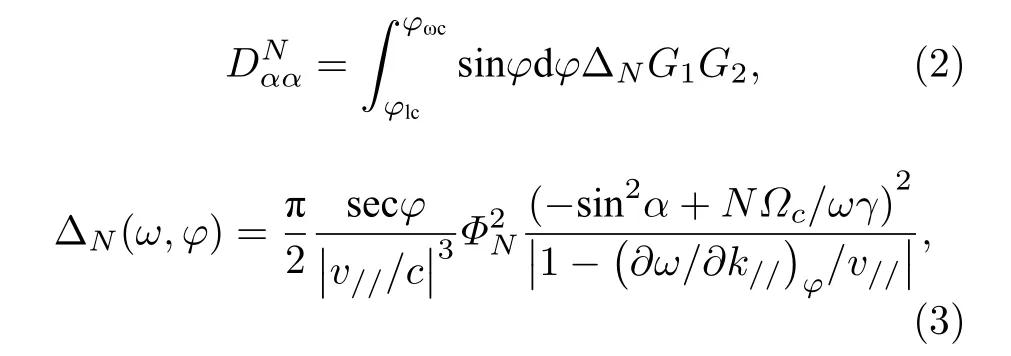
其中φN是波动电场和磁场的相关项[59],由于需要在粒子的弹跳路径上对局地投掷角扩散系数Dαα进行平均计算[60],于是有:

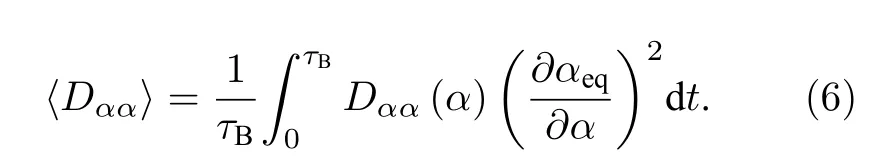
对于嘶声波的频谱分布,使用高斯频谱假设[9−10,28,52,59−61]具体表达式如下:

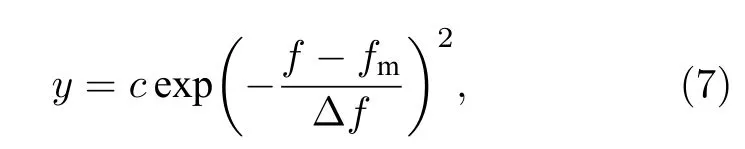
其中,fm为中心频率,Δf为带宽,f为频率,c为幅值参数,y为嘶声波的功率谱密度.本文中选取的具体参数是fm=500 Hz,Δf=300 Hz,f的范围是100—2000 Hz,幅值是10 pT.

对于嘶声波的传播角分布,采用两种传播角(φ)模型,分别为常数型传播角模型和随纬度变化的传播角模型[6].常数型传播角模型是一个不随纬度变化的高斯分布模型,主要参数为φm=0º,δφ=30º,0 ≤φ≤ 45º,其中φm为峰值传播角,δφ为带宽.随纬度变化的传播角模型是在不同磁纬度处选取不同高斯分布的模型,主要参数如表1 所示.

表1 随纬度变化的传播角模型主要参数Table 1.Parameters of the varying latitudinal wave normal angle model.

根据传播角模型,给出传播角模型表达式:

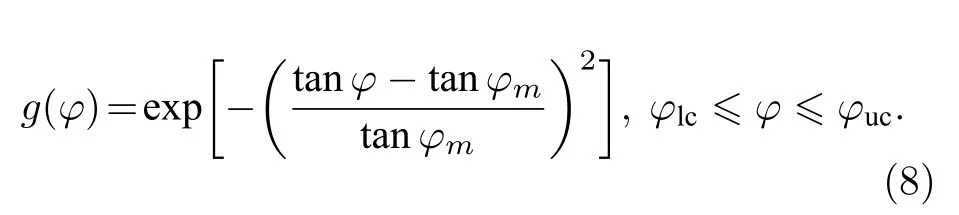
为了更方便调整嘶声波对辐射带电子散射系数数据库中的背景参数,本文引入背景参数α*,定义为等离子体频率(fpe)与电子回旋频率(fce)的比值,具体表达式如下:

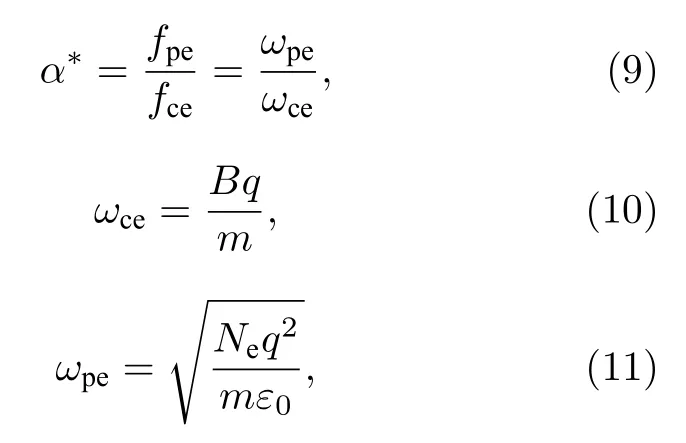
其中m为电子的质量,B为磁场强度,ε0为真空介电常数,q为元电荷,再引入偶极磁场模型(只考虑磁赤道面)可得:

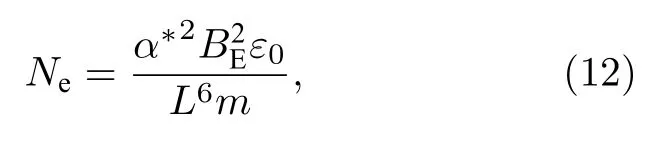
其中BE为地球表面赤道处磁场大小,BE=3.0911556× 10–5T.由(8)式可以得出Ne(电子密度)与L和α*的对应关系,如图1(a)所示.

本文利用FDC 计算了在不同L(1.5—5,分辨率为0.1)、α*(3—30,分辨率为1)、能级(10 keV—10 MeV)、λ(不同L的取值范围如表2 所示)、传播角模型以及赤道投掷角(0.5°—89.5°)上的嘶声波对辐射带电子散射系数,并整理得到散射系数矩阵数据库.

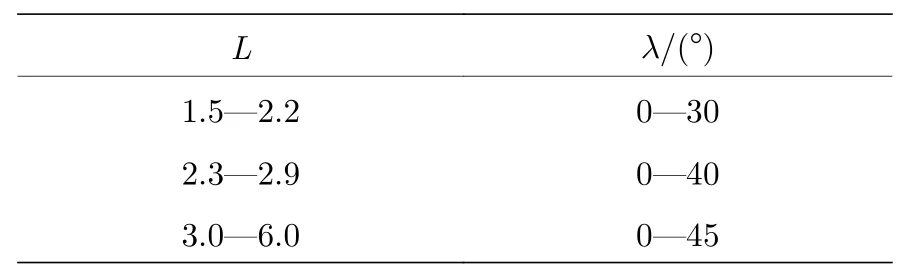
表2 不同L的磁纬度选取范围Table 2.Range of magnetic latitude at different L values.

Sheeley等[62]提出了地球偶极磁场下的等离子密度模型,具体公式为在等离子体层顶以内:

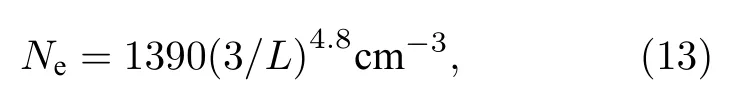
在等离子体层顶以外:

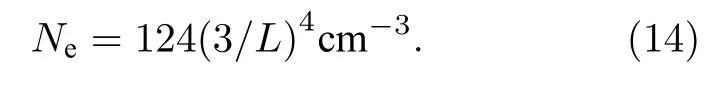
将(13)和(14)式代入(12)式,可以得到等离子体层顶以内和等离子体层顶以外的L和α*对应关系,即在等离子体层顶以内:

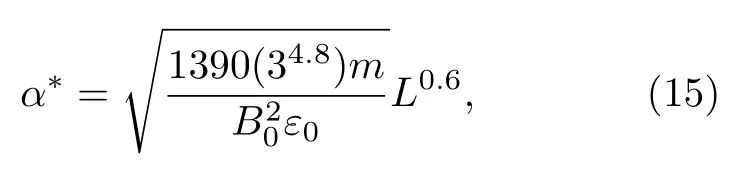
在等离子体层顶以外:

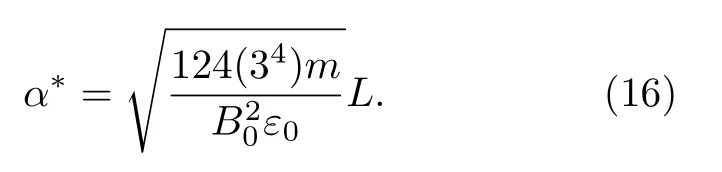
图1(b)展示了不同L下等离子体层以内和以外的α*的值,从图1(b)可以看出,本工作所建立的嘶声波对辐射带电子散射系数数据库所覆盖的α*值范围能够涵盖等离子体层顶以内和以外的情况.

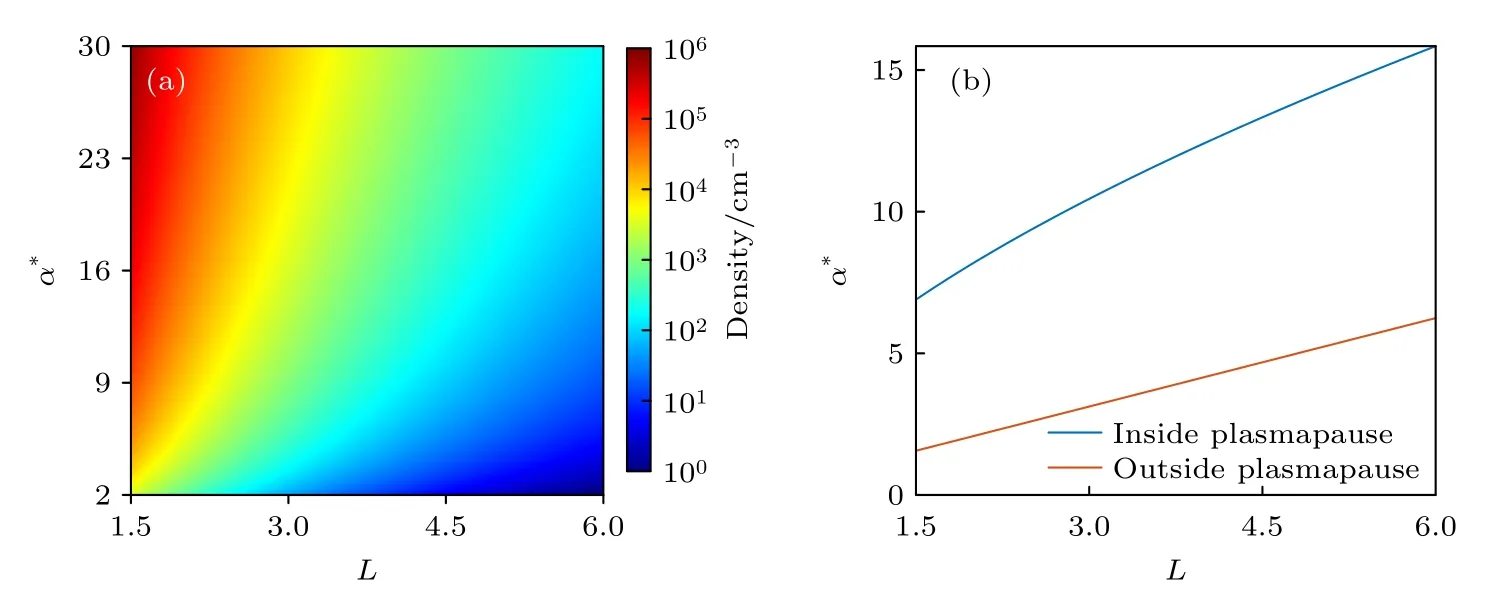
图1 (a)不同的L和α*条件下对应等离子体密度的数值;(b)不同L下α*的值,蓝线表示位于等离子体层以内,黄线表示位于等离子体层以外Fig.1.(a)The values of the density at different L and α* values;(b)the values of α* at different L,the blue line indicates inside the plasmapause and the yellow line indicates outside the plasmapause.

而对于需要研究的特定事件,本文所建立的嘶声波对辐射带电子的散射系数数据库中由于α*和L分辨率的限制,可能不能直接提供对应条件下的散射系数.为了满足快速获取特定事件下的嘶声波对辐射带电子的散射系数的需求,基于建立的散射系数数据库,可以通过线性插值方法得到任意α*和L情况下嘶声波对辐射带电子散射系数.本文采取的线性插值方法公式为

式中Y为所求散射系数值,X为所求散射系数对应的L(或α*)值,X1,X2为与X相邻的数据库网格点对应的L(或α*)值,Y1,Y2为与X1,X2对应的数据库内的散射系数.通过此线性插值方法,可以根据散射系数数据库快速插值得到在数据库区间内任意L,α*处的散射系数,从而提高计算散射系数的效率.

为了评估基于数据库线性插值结果的准确性,对比了特定参数下FDC 计算的散射系数结果与线性插值方法得到的散射系数结果,通过计算两者间的相对误差来反映插值结果的准确性,相对误差计算公式如下:

根据上文可知,弹跳平均投掷角散射系数与波幅的平方成正比,但是与磁壳数、背景电子密度等参数的关系较为复杂,不是简单的线性关系,改变输入参数不仅影响投掷角散射系数的大小,也改变它在能量和投掷角上的分布,因此通常需要花费大量的时间计算不同输入参数情况下嘶声波对辐射带电子的散射系数.正是由于计算投掷角散射系数对计算资源消耗较大,本文提出建立散射系数矩阵数据库,通过对数据库中的扩散系数进行插值处理,快速得到嘶声波在不同情况下对辐射带电子的散射系数,提高辐射带建模效率,可服务于空间天气现报和预报.

3 结果分析

根据FDC 计算得到嘶声波对电子的投掷角散射系数〈Dαα〉的数据库,图2—图9 分别展示了L=2,3,4和5的常数型传播角模型和随纬度变化传播角模型的弹跳平均投掷角散射系数〈Dαα〉.

图2 L=2 时常数传播角模型的嘶声波对电子的弹跳平均散射系数 〈Dαα〉,其中(a1)—(d7)分别对应不同α*条件下的散射系数Fig.2.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss waves for electrons with constant wave normal angle model at L=2,where(a1)–(d7)corresponds to the diffusion coefficients under different α* conditions,respectively.

图2 展示了用FDC 得到的L=2 时常数型传播角模型的弹跳平均投掷角散射系数〈Dαα〉,其中横坐标表示电子赤道投掷角αeq,纵坐标表示电子能量Ek.从图2 可知,嘶声波对辐射带电子的散射作用主要分为两方面,一方面是通过回旋共振影响中低投掷角电子,另一方面是通过朗道共振影响高投掷角电子.当α*=3,回旋共振影响辐射带电子能级范围为1—10 MeV.随着α*的提升,影响的能级范围不断增大.当α*=30时,回旋共振影响辐射带电子能级扩展到了50 keV—8 MeV,但是在低投掷角高能级处(大于1 MeV)的散射系数只有10–9s–1,小于α*=3 时的散射系数10–7s–1.嘶声波通过回旋共振影响的辐射带电子投掷角范围随着能级降低而减小.当α*=3时,散射系数最大值达到10–7s–1且集中在1—8 MeV 电子能级范围内.当α*=30 时散射系数最大值达到10–6s–1分布在100 keV左右电子能级范围,相对于低α*散射系数最大值对应的能级较低.对于嘶声波通过朗道共振影响的辐射带电子散射系数,α*=3 时影响的能级范围大于10 keV,随着α*的增大低能级电子的散射系数增强,而高能级电子的散射系数下降,并且低能级位置的散射系数逐渐向90°移动.

图3 展示了当L=3 时的常数型传播角模型投掷角散射系数〈Dαα〉.嘶声波对辐射带电子的散射作用与L=2 时一样分为两方面.当α*=3,回旋共振影响辐射带电子能级范围在800 keV—10 MeV.随着α*的提升,影响的能级范围不断增大.当α*=30时,回旋共振影响辐射带电子能级扩展到了9 keV—1 MeV.但是随着α*的提升,强散射系数对应的能级逐渐降低.对于嘶声波通过朗道共振影响的辐射带电子散射系数,变化特征与图2中L=2 时的变化特征类似,随着α*的提升,强散射系数对应的位置逐渐向低能级、高投掷角移动.图2和图3 中嘶声波的波幅均为10 pT,但是图3 中的散射系数计算结果普遍高于图2,说明在较高的L,嘶声波的扩散效应更明显.

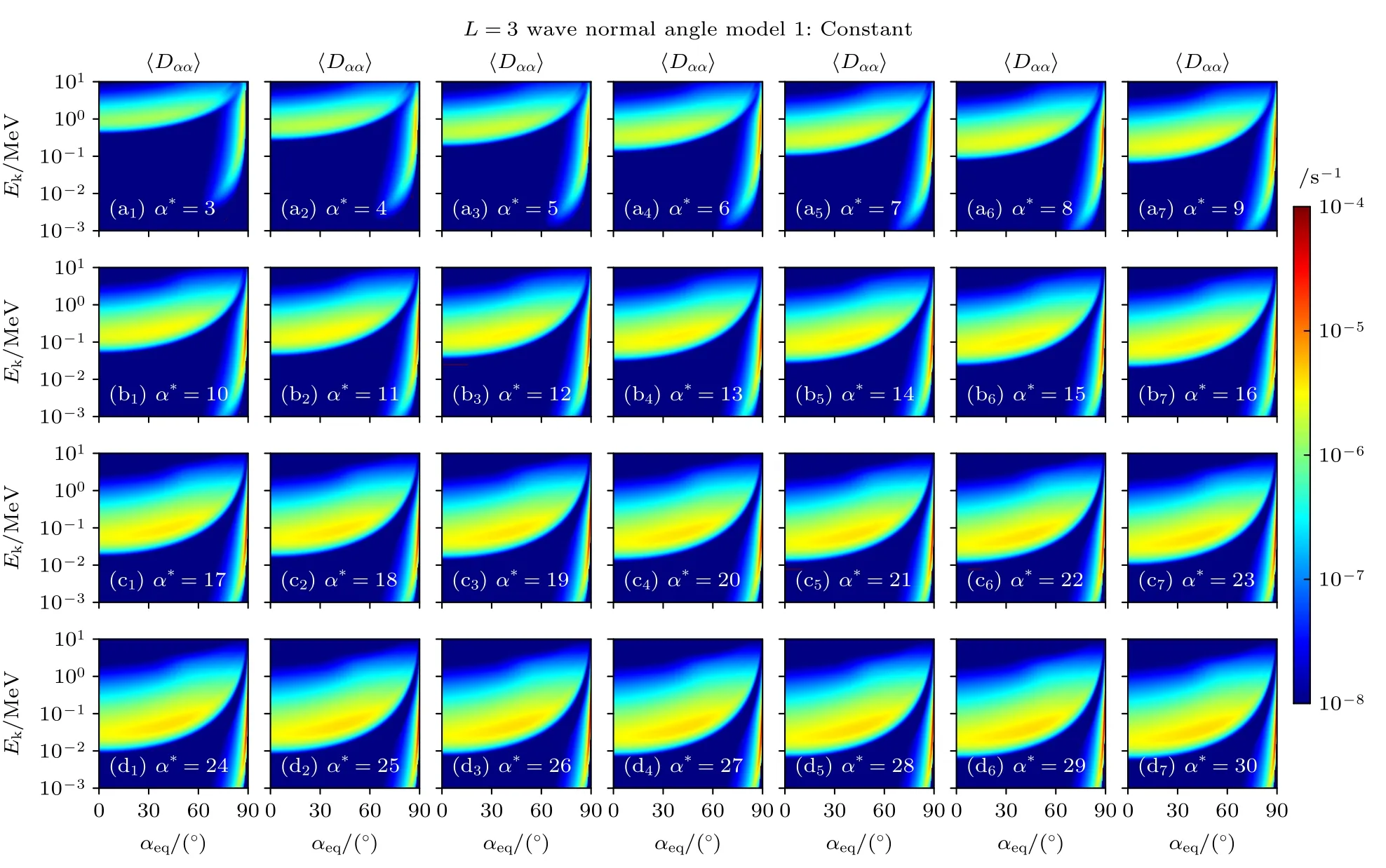
图3 L=3 时固定传播角模型的嘶声波对电子的弹跳平均散射系数 〈Dαα〉,其中(a1)—(d7)分别对应不同α*条件下的散射系数Fig.3.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss waves for electrons with constant wave normal angle model at L=3,where(a1)–(d7)corresponds to the diffusion coefficients under different α* conditions,respectively.

图4和图5 分别展示了当L=4和L=5 时的常数型传播角模型投掷角散射系数〈Dαα〉.同样嘶声波对辐射带电子的散射作用主要分为回旋共振影响的中低投掷角电子和通过朗道共振影响高投掷角电子.在α*相同的情况下,随着L的增大,回旋共振影响的能量范围逐渐下降.L=4时,回旋共振影响的能级范围为3 keV—1 MeV;L=5时,回旋共振影响的能级下降至1 keV—1 MeV.朗道共振影响的范围随着L的改变也发生变化,但始终在高投掷角区域.随着L的增大,嘶声波对电子的散射系数不断增强.L=4时〈Dαα〉最高值为10–5s–1,当L=5时〈Dαα〉最高值为5× 10–5s–1.

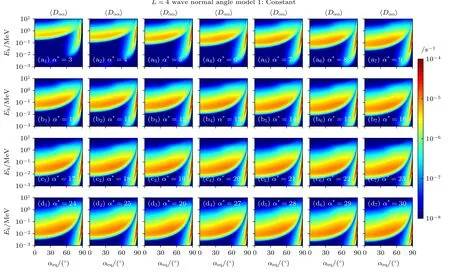
图4 L=4 时常数传播角模型的嘶声波对电子的弹跳平均散射系数 〈Dαα〉,其中(a1)—(d7)分别对应不同α*条件下的散射系数Fig.4.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss waves for electrons with constant wave normal angle model at L=4,where(a1)–(d7)corresponds to the diffusion coefficients under different α* conditions,respectively.

图6—图9 展示了当L=2,3,4,5 时用随纬度变化型传播角模型计算的弹跳平均投掷角散射系数〈Dαα〉.对比图6 与图2,回旋共振部分基本一致,朗道共振部分变化较大.当α*=3时,散射系数最大值小于10–7s–1;α*=30时,散射系数最大值达到10–7s–1数量级,均小于图2 对应α*处的散射系数值.图7—图9 与对应图3—图5 对比,回旋共振部分基本一致,朗道共振部分变化较大.朗道共振散射系数最大值在对应α*处减小,并且出现多条带状结构,这是常数型传播角未出现的现象.

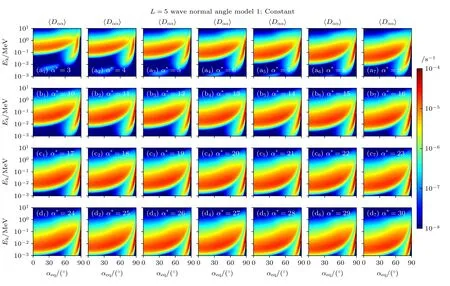
图5 L=5 时固定传播角模型的嘶声波对电子的弹跳平均散射系数〈Dαα〉,其中(a1)—(d7)分别对应不同α*条件下的散射系数Fig.5.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss waves for electrons with constant wave normal angle model at L=5,where(a1)–(d7)corresponds to the diffusion coefficients under different α* conditions,respectively.

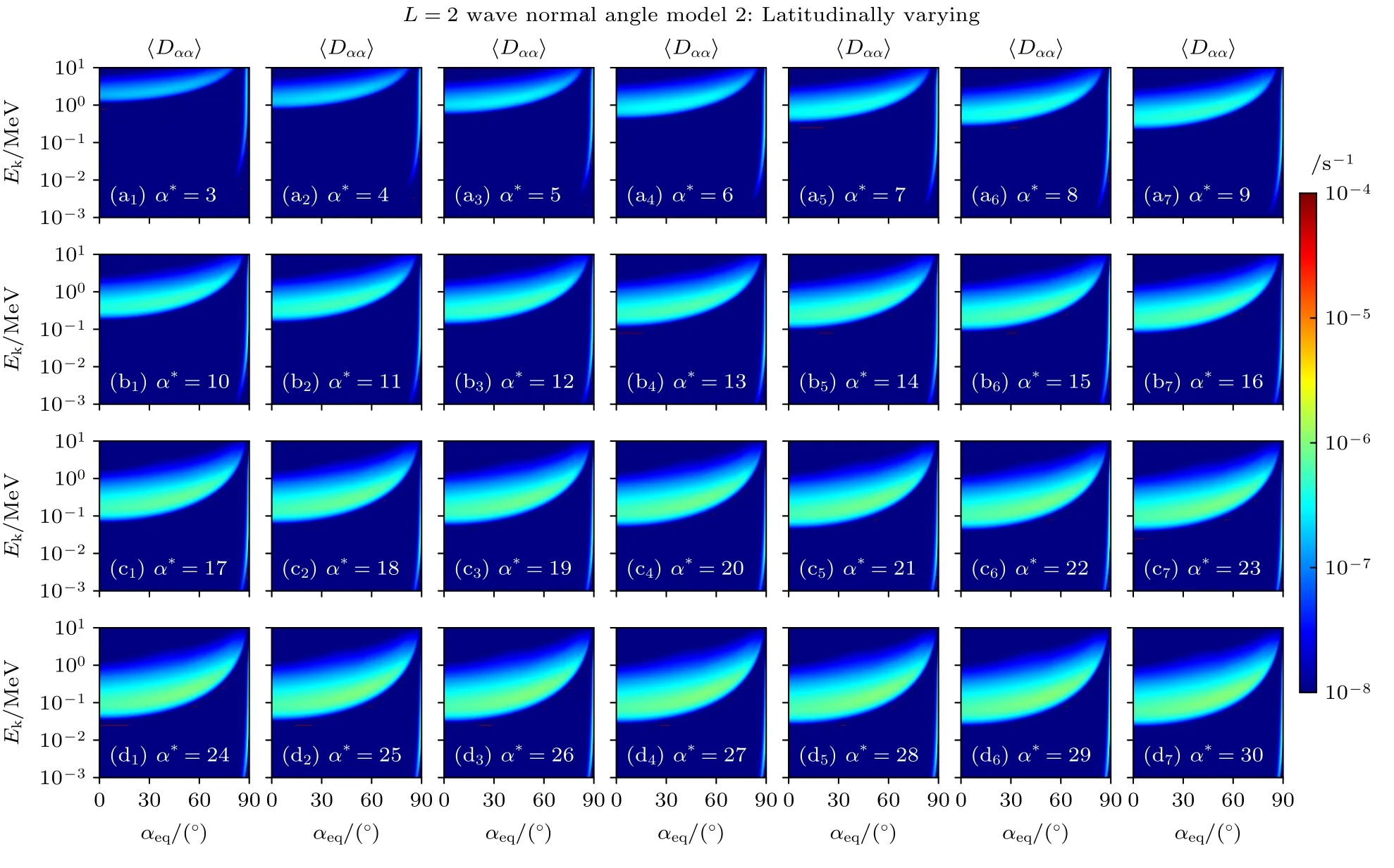
图6 L=2 时随纬度变化传播角模型的嘶声波对电子的弹跳平均散射系数 〈Dαα〉,其中(a1)—(d7)分别对应不同α*条件下的散射系数Fig.6.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss waves for electrons with latitudinally varying wave normal angle model at L=2,where(a1)–(d7)corresponds to the diffusion coefficients under different α* conditions,respectively.

图7 L=3 时随纬度变化传播角模型的嘶声波对电子的弹跳平均散射系数 〈Dαα〉,其中(a1)—(d7)分别对应不同α*条件下的散射系数Fig.7.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss waves for electrons with latitudinally varying wave normal angle model at L=3,where(a1)–(d7)corresponds to the diffusion coefficients under different α* conditions,respectively.

图8 L=4 时随纬度变化传播角模型的嘶声波对电子的弹跳平均散射系数 〈Dαα〉,其中(a1)—(d7)分别对应不同α*条件下的散射系数Fig.8.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss waves for electrons with latitudinally varying wave normal angle model at L=4,where(a1)–(d7)corresponds to the diffusion coefficients unde?r different α* conditions,respectively.

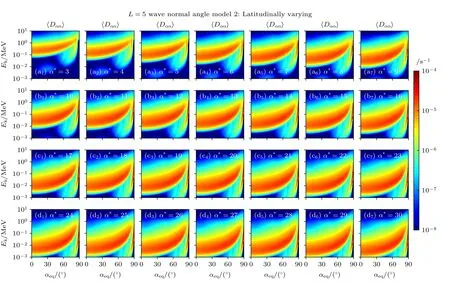
图9 L=5 时随纬度变化传播角模型的嘶声波对电子的弹跳平均散射系数〈Dαα〉,其中(a1)—(d7)对应不同α*条件下的散射系数Fig.9.Bounce averaged diffusion coefficients 〈Dαα〉 of hiss wa ves for electrons with latitudinally varying wave normal angle model at L=5,where(a1)–(d7)corresponds to the diffusion coefficients under different α* conditions,respectively.

综上,在相同传播角模型和L下,随着α*的增大,嘶声波通过回旋共振对辐射带电子的散射作用影响的能级范围增大,散射系数增大;通过朗道共振的结果受α*影响相对较小.在相同传播角模型和α*下,随着L的增大,嘶声波通过回旋共振对辐射带电子的散射作用影响的能级范围增大,散射系数增大;通过朗道共振影响的辐射带电子散射系数增大,投掷角范围也有所增大.不同传播角模型回旋共振作用的结果影响较小,朗道共振受传播角模型的影响较大.在相同的L和α*的条件下,随纬度变化的传播角模型朗道共振作用部分的散射系数小于常数型传播角模型对应能级的数值,并且影响的投掷角范围较大,由于不同纬度采取的传播角模型不同,导致出现多个条带状结构.

4 基于嘶声波散射系数矩阵数据库线性插值误差分析

基于第3 节计算的嘶声波对辐射带电子的散射系数矩阵数据库,计算了数据库线性插值结果与FDC 计算结果的相对误差.本文选取6 组数据,即选定α*=4,取L=3.25,L=4.35,L=5.55,以及选定L=4,分别选取α*=3.25,α*=4.35,α*=5.55 来展示对比结果,这里均采用了随纬度变化的传播角模型结果.图10—图13 分别展示了不同参数下FDC 计算结果与基于数据库线性插值结果对比.

图10 (a1)—(a3)当α*=4时,L=3.25,L=4.35,L=5.55 处计算得到的嘶声波散射系数;(b1)—(b3)通过数据库进行线性插值计算得到的嘶声波散射系数;(c1)—(c3)二者相对误差分析Fig.10.(a1)–(a3)The diffusion coefficients of hiss waves calculated at L=3.25,L=4.35,L=5.55 when α*=3;(b1)–(b3)the hiss wave diffusion coefficients calculated by linear interpolation from the database;(c1)–(c3)the relative error analysis.

选定α*=4时,不同L值的3 组结果如图10所示.当L=5.55 时FDC 计算结果基本与插值结果无异,当L=4.35和L=3.25 时有少许误差.通过对误差数值分析,在L=3.25、能级在1 MeV的高误差处,由于本身散射系数较小,小于10–8s–1,存在误差量级较小.图11 选取了能级为50 keV,200 keV,400 keV 以及700 keV 电子的散射系数进行对比,与图10 结果类似,L=5.55 时不同能级电子的散射系数FDC 计算结果与线性插值结果差异最小,此外700 keV 电子的散射系数在不同的L值下相对误差均最小.综合图10和图11 对比结果,整体上线性插值结果与FDC 计算结果基本吻合,说明采用线性插值方法的可靠性,且得到的结果有较高的准确性.

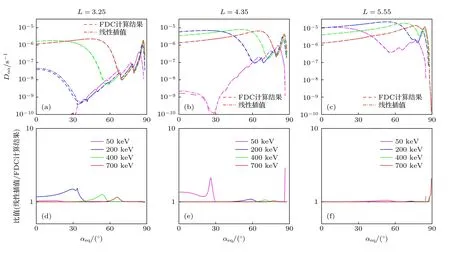
图11 (a)—(c)当α*=4时,L=3.25,L=4.35,L=5.55 处选取能级为50 keV,200 keV,400 keV 以及700 keV的散射系数对比结果;(d)—(f)数值的比值,虚线表示FDC 计算结果,点画线表示线性插值结果,不同颜色代表不同能级Fig.11.(a1)–(a3)Comparison of the diffusion coefficients at α*=4,L=3.25,L=4.35,L=5.55 for selected energy levels of 50 keV,200 keV,400 keV and 700 keV;(d)–(f)the ratio of values,the dashed line shows the result of the FDC calculation,the dotted lines shows the result of linear interpolation,different colors represent different energy levels.

选定L=4时,不同α*值的3 组结果如图12所示,从图12(c1)—(c3)可以看出,当α*=5.55,α*=4.35和α*=3.25 时有部分较大误差.对高误差数值进行分析,主要原因是由于线性插值在计算边界结果存在局限性所致,但是在误差率较大处的误差值很小,小于10–7s–1是可以接受的范围.图13 展示了具体能量的数值比较结果,在50 keV与200 keV 出现较大误差,而能级处的电子散射系数较小,也是造成相对误差较大的原因.而其余大部分散射系数的线性插值结果与FDC 计算结果接近,证明了线性插值结果较为准确.综上所属,基于本文建立的嘶声波对辐射带电子的散射系数数据库,可以通过线性插值方法快速获得不同地磁条件不同空间区域嘶声波对电子的散射系数,极大降低了计算量,提高了后续进行辐射带建模的效率.

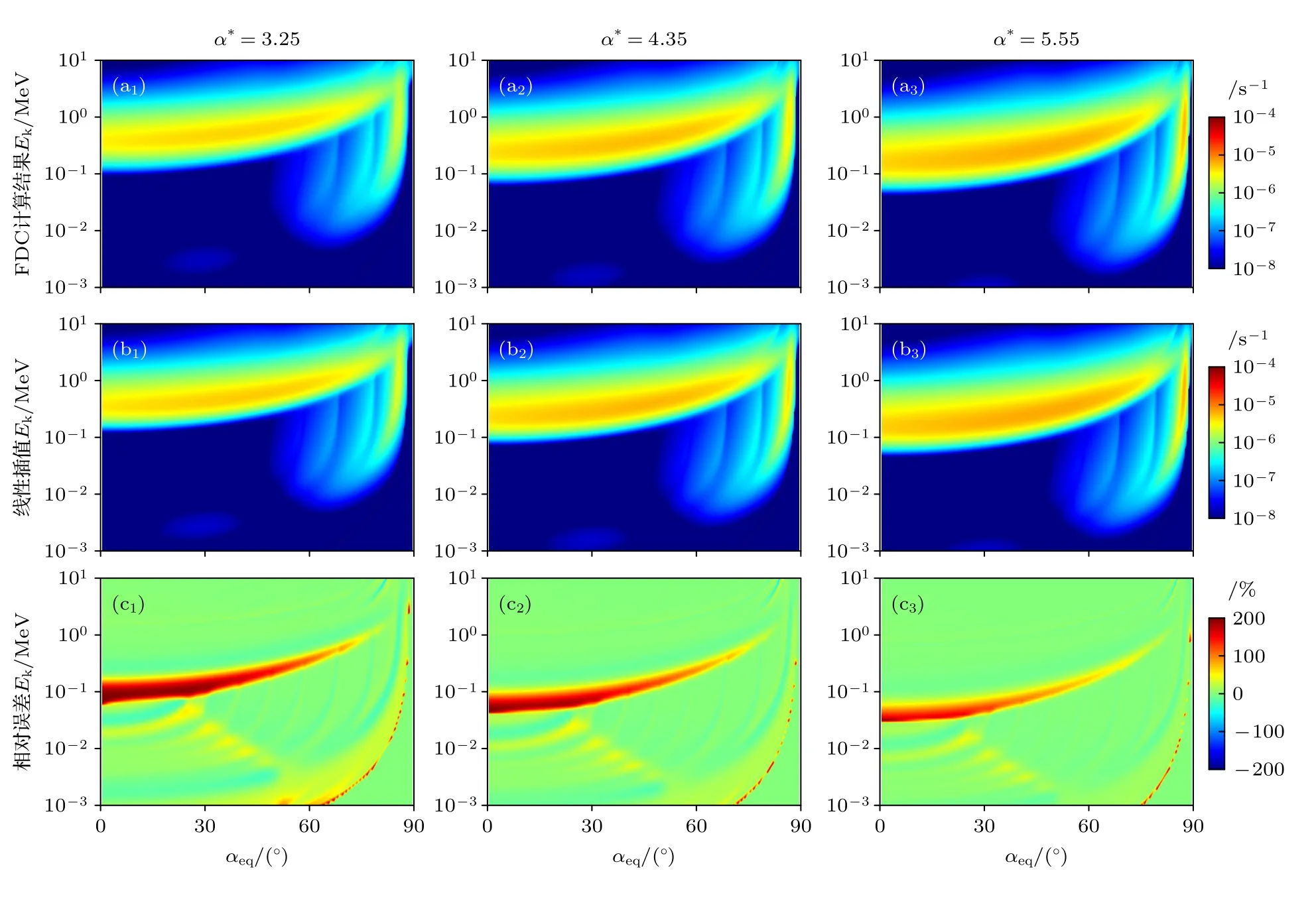
图12 (a1)—(a3)当L=4时,α*=3.25,α*=4.35,α*=5.55 处计算得到的嘶声波散射系数;(b1)—(b3)通过数据库进行线性插值计算得到的嘶声波散射系数;(c1)—(c3)表示对二者进行相对误差分析Fig.12.(a1)–(a3)The diffusion coefficients of hiss waves calculated at α*=3.25,α*=4.35,α*=5.55 when L=4;(b1)–(b3)the hiss wave diffusion coefficients calculated by linear interpolation from the database;(c1)–(c3)the relative error analysis.

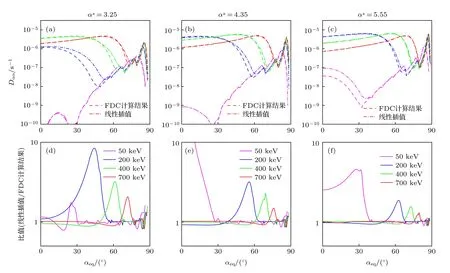
图13 (a)—(c)当L=4时,α*=3.25,α*=4.35,α*=5.55 处选取能级为50 keV,200 keV,400 keV和700 keV的散射系数对比结果;(d)—(f)数值的比值,虚线表示FDC 计算结果,点画线表示线性插值结果,表示不同颜色代表不同能级Fig.13.(a)–(c)The comparison of the diffusion coefficients at α*=3.25,α*=4.35,α*=5.55 for L=4 for selected energy levels of 50 keV,200 keV,400 keV and 700 keV;(d)–(f)the ratio of values,the dashed line shows the result of the FDC calculation,the dotted lines shows the result of linear interpolation,different colors represent different energy levels.

5 结论

本文基于FDC 程序,建立了在L=1.5—6,α*=3—30 范围内嘶声波对辐射带电子散射系数矩阵数据库.展示了L为2,3,4和5,α*为3—30的两种传播角模型的嘶声波对辐射带电子散射系数并对结果进行讨论.以此散射系数数据库为基准,通过线性插值得到几组随机选定参数的散射系数,并与通过FDC 计算方法直接计算得到的散射系数进行比较,验证了线性插值结果的有效性.

1)在相同传播角模型和L下,随着α*的增大,嘶声波通过回旋共振对辐射带电子的散射作用影响的能级范围增大,散射系数增大,随着能级降低,影响的投掷角范围也降低;而通过朗道共振的结果受α*影响相对较小,基本影响电子所有能级,影响投掷角范围集中在90º附近.

2)在相同传播角模型和α*下,随着L的增大,嘶声波通过回旋共振对辐射带电子的散射作用影响的能级范围增大,散射系数增大;通过朗道共振影响的辐射带电子散射系数增大,投掷角范围也增大,但不低于60º.

3)在相同α*和L下,不同传播角模型对于嘶声波通过回旋共振作用的结果影响较小,而嘶声波通过朗道共振作用受传播角模型的改变影响较大,随纬度变化的传播角模型相对常数型传播角模型,散射系数减小,但投掷角范围增大,并且出现了多个条带状结构.

4)通过对线性插值结果与直接通过FDC 计算方法得到的结果进行误差分析,在大部分电子共振区间误差较小.结果表明本文建立的嘶声波对辐射带电子散射系数矩阵数据库可以通过线性插值快速得到在不同L和α*处的有效散射系数.这显著提升了辐射带建模效率.