核磁共振陀螺中EPR 信号响应不对称性研究*
鱼在洋 郑锦韬 张洋 汪之国† 孙辉 熊志强 罗晖
1)(陕西师范大学,物理学与信息技术学院,西安 710049)
2)(国防科技大学前沿交叉学科学院,长沙 410073)
3)(国防科技大学量子信息学科交叉中心,长沙 410073)
核磁共振陀螺具有高精度、小体积、低功耗等优点,是目前陀螺仪研究领域的热点之一.陀螺中的碱金属原子自旋弛豫时间通常在10–5 s 量级,远小于在通常原子磁力仪中的弛豫时间.研究了短弛豫时间原子自旋对不同方向的振荡磁场EPR 响应的差异,分析了基于EPR 信号测量中心频率方法的偏差与弛豫时间的关系,并从理论上给出了修正.提出了一种基于XY 轴信号相位差测量横向弛豫时间的方法,可以实现对弛豫时间的准确快速测量.在实验上以87Rb 原子为例比较了几种测量方式的准确性和适用性,其中半高宽拟合法受到系统延迟时间的影响较大并有其测量极限,相位测量法受到探测光角度影响较大,但测量范围更广,且抗干扰能力更强.研究对于准确测量核磁共振陀螺参数,提高陀螺性能的研究具有重要意义.
1 引言
陀螺仪作为惯性导航系统的核心器件,在车辆、船舶、卫星以及国家安全方面都有着重要的应用[1−3].传统成熟的高精度陀螺仪包括转子陀螺以及激光陀螺,其精度在20 世纪80 年代就可以分别达到 10−6(°)/h和 10−4(°)/h[4],但在之后进入平台期[5].近年来,随着量子精密测量技术的逐渐发展,原子陀螺仪在精度,体积以及稳定性上都得到了快速的发展,逐渐成为该领域的研究热点[6−8].
本文所研究的核磁共振陀螺仪(nuclear magnetic resonance gyroscope,NMRG)具有高精度、高稳定性、小体积的优势,具有很好的发展前景和应用潜力,其报道精度最高可达 0.01(°)/h[9−11].NMRG通过外界磁场驱动核自旋产生的稳定的拉莫尔进动作为参考以测量载体转动的角速度,并采用光的法拉第旋转效应探测该进动频率[12].其灵敏度主要受到原子气室内的磁场梯度以及原子自旋的弛豫时间制约,其中磁场梯度会引起共振频率的漂移从而导致偏差[13],弛豫时间则会受到原子的密度,磁场梯度以及温度等因素的共同影响[14].理论上,核自旋的弛豫时间越长则具有更窄的线宽,因此可以达到的灵敏度极限越高[15].此外,准确且快速的测量弛豫时间的变化,对于提高系统的零偏稳定性等指标有着重要的作用.NMRG 通常使用碱金属原子如87Rb 原子的自旋极化去测量惰性气体原子如129Xe 以及131Xe 核自旋的核磁共振信号.系统中的碱金属原子弛豫时间通常在 10−5s 量级,需要通过测量其电子顺磁共振(electron paramagnetic resonance,EPR)信号来获取其共振频率及线宽等参数.现有的弛豫时间测量方法包括自由感应衰减和自旋回波法[16],对于这样极短的弛豫时间需要系统有极高的采样率以稳定的外界环境[17,18].此外还可以通过测量吸收曲线估计弛豫时间,这种方法会受到磁场变化和系统传输延迟的干扰而产生偏差,对实验系统的稳定性要求较高.
在现有的实验中通常采用振荡磁场作为外界驱动磁场以测量EPR 信号,本文从理论上分析了振荡磁场与旋转磁场作用下原子进动的幅频响应的相位响应差异,发现了振荡磁场下原子EPR 信号在响应的不对称性,并且在实验中进行了验证,得到了与理论比较一致的结果.这表明探测光与磁场的相对角度变化会引起陀螺仪响应的变化.此外,利用这种响应的差异,提出了一种基于XY轴信号相位差的弛豫时间测量方法,这种方法对于测量非常短的弛豫时间有较高的准确性,并且对于磁场强度的波动不敏感,具有较高的稳定性.
2 振荡磁场与原子自旋的相互作用理论
2.1 理论模型
以87Rb 原子为例,在与原子塞曼能级共振的磁场驱动下,会驱动其核外电子产生EPR 信号[19,20],弱磁环境下,碱金属原子自旋与核外电子自旋相互耦合,对外表现为原子的总自旋磁矩的进动.可以用布洛赫方程描述振荡磁场与原子磁矩的相互作用过程[21−23],对于磁矩为M=[MX,MY,MZ]T的原子,在垂直于静磁场的方向施加交变的弱磁场,这会引起原子的磁矩做周期性运动:
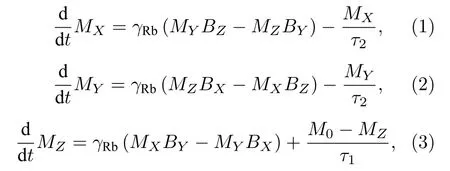
其中τ2,τ1分别为横向和纵向弛豫时间,γRb为原子的旋磁比.静磁场沿着Z轴方向Bz=B0.振荡磁场可以分解为围绕着Z轴转动的磁场:

其中B±分别表示左旋和右旋方向,Beff是施加振荡磁场的强度.在左右旋磁场作用下磁矩横向分量的稳态解分别为

式中 ∆ω=ω0−ω1,∆ω′=ω0+ω1分别对应左右旋场的频率与拉比频率的差,ω0=γRbBo.并且忽略τ1τ2(γBeff)2这一项以简化计算,对于所讨论的情况,实际上弛豫时间与拉比频率之积τ2ω0的量级接近于1,但由于施加的振荡磁场相较于静磁场很弱,因此有τ1τ2(γBeff)2≪1.将(5)和(6)式的结果合并,可以得到XY轴上原子磁矩大小随时间的变化:

可以看出,尽管在形式上相近,但XY轴的响应函数仍有不同,尤其对于弛豫时间较短的原子,∆ω′τ2≫1的条件不成立,此时两轴的响应差异就十分明显.为了方便计算,定义a=ω1τ2;b=ω0τ2,并假设中心频率ω0不随时间改变,将响应函数写成关于参量a函数,有:

其中a,b都是大于0的实数.与旋转磁场相比,XY轴的幅值响应并不会在共振条件a=b时达到极大值,这意味通过测量响应峰值来确定共振频率的方法会出现偏差.对中心频率为70 kHz的87Rb 原子,在不同弛豫时间下振荡场的XY轴幅频响应差异以及与旋波场的差异仿真结果如图1 所示,∆ω <0时X轴上信号强度要高于Y轴,信号最大值对应的频率也低于ω0.

图1 振荡场与旋转场的幅频响应(a);(b);(c);(d)τ2=10 μs τ2=20 μs τ2=50 μs τ2=100 μs.τ2=10 μs τ2=20 μs τ2=50 μs τ2=100 μsFig.1.Amplitude-frequency responses of oscillating and rotating fields(a);(b);(c);(d)
通过分别求解两轴响应函数的极大值所对应的磁场频率,可以得到两轴中心频率与拉比频率的差值:

从(15)和(16)式可以看出,原子的横向弛豫时间越短,产生的中心频率移动就会越明显.从之前的分析可以看出,以振荡场驱动时原子磁矩实际的进动轨迹是一个椭圆形,利用(13)和(14)式容易求得其长短轴之比h=.因此对于给定频率的磁场,横向弛豫时间越短,其两轴的响应强度差异就越大.
3 系统传输延迟及弛豫时间测量
3.1 系统传输延迟测量
对一个测量系统,总是会存在传输延迟t0,它是系统从输入信号开始到得到输出信号的时间差,在磁力仪系统中,传输延迟主要表现为输入信号与输出信号的相位差,由于对同一个系统,传输延迟是一个随时间和输入信号基本不变的量,因此对于不同的频率,会产生相位延迟 ∆φ=ω1t0.理论上,通过测量输出信号与理想输出信号的相位差,就可以测得传输延迟.但实际上在系统的参数未知的情况下,求解理想的输出信号往往是较为困难的.但利用磁力仪两轴响应的不对称性,可以在未知系统参数的情况下,求解系统的传输延迟.利用(13)和(14)式,可以分别求解相位的零点以及中心频率,发现对应Y轴相位零点的频率同时对应X轴的峰值频率:
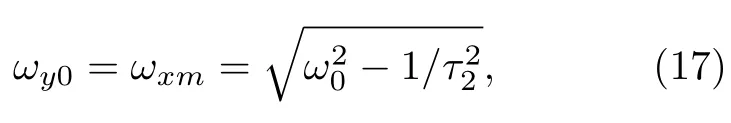
其中ωy0为Y轴相位为0是对应的频率,ωxm为X轴信号响应最大值对应的频率.通过扫频可以容易的得到ωxm的值,此时仅需改变磁场的方向,在Y轴施加磁场并测量输出信号的相位就可以容易的得到系统的传输延迟:

其中φ0为对应于X轴最大响应强度的频率ωxm的振荡场施加在Y轴时测量得到的相位,即使不确定系统的中心频率和弛豫时间,依然可以采样这种方法较为准确地测量系统的传输延迟.
3.2 弛豫时间测量
横向弛豫时间的测量主要有自由感应衰减(FID),自旋回波以及半高宽估计法等几种,在原子磁力仪中,碱金属原子的弛豫时间通常极短(在微秒及微秒以下),前两种估计方法对测量设备的精度以及采样速率有着较高的要求,而基于布洛赫方程理论的半高宽估计法需要测量吸收曲线即(6)式中的正弦项.通过对输出信号做正交分解得到吸收曲线,从而得到估计:

其中 ∆ωha为吸收曲线的半高宽.由于系统总会有一定的传输延迟t0,这会在不同的频率下引起不同的相位延迟,从而导致吸收曲线的测量出现误差.另一方面,实验中往往采用振荡场替代旋波场,取幅频响应的最大点作为相位零点,考虑到反旋项的影响,得到的频率点相位不为0,因此正交分解得到的吸收曲线会存在偏差.
利用之前的计算,可以从不依赖相位的幅频响应出发,对系统弛豫时间做出估计.从(13)和(14)式出发,可以对响应函数的半高宽进行求解:

从而得到弛豫时间与幅频曲线半高宽的关系:

通过测量信号幅频曲线的半高宽就可以直接求出横向弛豫时间.对于弛豫时间很短的原子,其吸收和幅频曲线展宽很大,即使在0 Hz 附近的信号也高于最大值的一半,因此无法测量其半高宽,利用其幅频特性测量弛豫时间的方法是不可行的.通过计算可知,对参数b <10的范围,利用吸收曲线测量弛豫时间会出现较大的偏差,而利用幅频曲线则可以在b >3.73的范围内测量,理论上具有更大的测量范围.
此外,根据相位关系同样可以计算弛豫时间,从(13)和(14)式出发计算XY轴上信号相位的差异,注意到两个轴上相位的差满足:
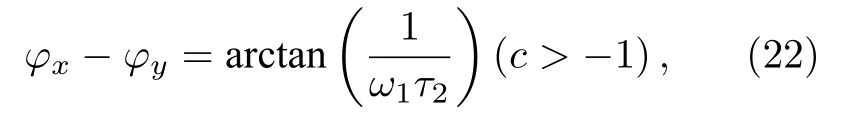
其中c=tan(φx)tan(φy),这表示XY轴的相位差取决于原子的弛豫时间,因此通过改变探测轴或改变振荡场方向,测量相位差就可以求出弛豫时间:

由于相位的相减消去了由于系统传输延迟带来的误差,因此这种测量方法受到系统参数波动的影响较小.
在微弱磁场下,理论上3 种方式都有较高的估计精度,但是在实验中,测量吸收曲线的过程会受到传输延迟的影响,从而导致吸收曲线出现对中心频率的不对称,并且峰值减小的情况,这会导致测量的弛豫时间与实际出现偏差,即使通过在共振点进行相位补偿消去此时的响应相位,由于不同频率对应的响应相位不同,在实验中直接而准确地测量吸收曲线是相对困难的.
除了传输延迟,还需要考虑实验中探测光与磁场的方向不一定完全垂直,理论上我们假设探测光轴与施加磁场的X轴是重合的,但在实验上,探测光轴与磁场的X 轴并不会完全重合,一方面是由于难以将光轴准确沿着磁场方向进行校对,从而使其完全平行,另一方面由于存在剩余磁场的干扰,这些干扰因素会改变原子实际受到的磁场,从而使探测光轴与施加磁场的方向出现偏移,从而引起信号的相位变化.假设存在偏转角φ,对于沿着X轴施加的磁场,实际探测得到的响应函数和相位是一个与偏转角相关的函数:

由图2 可知,相同偏转角度引起X,Y轴上相位变化存在差别,这导致了由相位估计的弛豫时间发生变化.不同频率下的估计值随偏转角大小的变化如图,从仿真结果发现,在且仅在ϕ=0处,不同频率下估计得到的弛豫时间与理论值相同.

图2 偏转角度对测量精度的影响Fig.2.Effect of deflection angle on measurement accuracy.
4 实验部分
实验上通过法拉第旋转效应探测87Rb 原子的宏观磁矩变化[12],在于泵浦光垂直的方向施加一束较弱的线偏振光,由于原子宏观极化导致对左右旋光的吸收率不同,经过气室后探测光旋转角度θ与该方向的原子磁矩成比例:

式中nAσ0为气室光学深度的倒数,L为光与原子作用的光程,W为跃迁线宽,∆为探测光的共振偏移量,P∞为探测光的线偏度.通过测量探测光的角度偏移量,就可以测量原子磁矩随时间的变化特性.实验装置如图3 所示,内边长约10 mm的方形原子气室置于磁屏蔽桶内部,包含大量87Rb 以及约5 Torr(1 Torr≈133.322 Pa)的129Xe,45 Torr的131Xe,此外还充入N2作为缓冲气体;由一个亥姆霍兹线圈提供磁场以及高频载波场,泵浦光波长为795 nm,强度约100 mW,经过线偏片(Linear polarizer,LP)以及λ/4 波片变为圆偏光后再经过扩束系统后沿着Z轴入射气室,同时一束波长795 nm,强度约700 μW的探测光经过线偏片起偏后射入气室与原子相互作用,再由沃伦斯顿棱镜(Wollanston prism,WP)分束后进入平衡探测器(balance detecter,BD)测量法拉第旋转角θ,得到的信号再经由信号处理系统进行分析.

图3 实验装置Fig.3.Experiment settings.
4.1 磁共振信号响应曲线测量
利用亥姆霍兹线圈在Z轴上施加约 11.7 μT的恒定静磁场,分别在X轴上和Y轴上分别施加约10 nT的振荡磁场,并通过磁通门标定该磁场,确保XY轴上施加的磁场大小相同.通过分别改变XY轴磁场频率得到的幅值响应曲线见图4(a),在偏离共振点的频率可以明显看出,不同方向磁场下原子的共振信号强度不同,此外中心频率的位置也发生了偏移,两个方向上的频率差为101.4 Hz.同时通过鉴相器测量的信号相位差如图4(b),信号相位受到磁场频率的影响较大,在扫频过程中会出现较大波动,但对于固定的磁场频率相位的波动很小,大约在 0.001°.另外相位差并不等于磁场角度的变化值,这与第2 节结果一致.

图4 幅频及相位响应曲线测量(a)幅频响应;(b)相位响应Fig.4.Amplitude-frequency and phase-frequency curve measurement(a)Amplitude-frequency curve;(b)phase-frequency curve.
4.2 系统传输延迟及弛豫时间测量
通过在X轴上进行磁场扫频,测量得到对应最大响应的频率点为84.5853kHz(如图4),此时改变磁场方向,在Y轴上施加与X轴幅频响应最大点相同频率的振荡场,对输出信号的相位进行测量为− 44.06(1)°,根据(18)式,此时测量得到的相位就等于由于信号传输延迟产生的相位延迟,通过计算得到系统的传输延迟时间约为1.44(7)μs.为验证测量结果的准确性,通过锁相放大器输出磁场信号,先经过采集卡施加固定的时间延迟后再输出到线圈上.对比不同的延迟时间测量输出信号的相位变化,得到的实验结果如图5,相位与延迟时间呈线性相关,1 μs的延迟时间大约会导致信号产生30.5°的相位延迟.
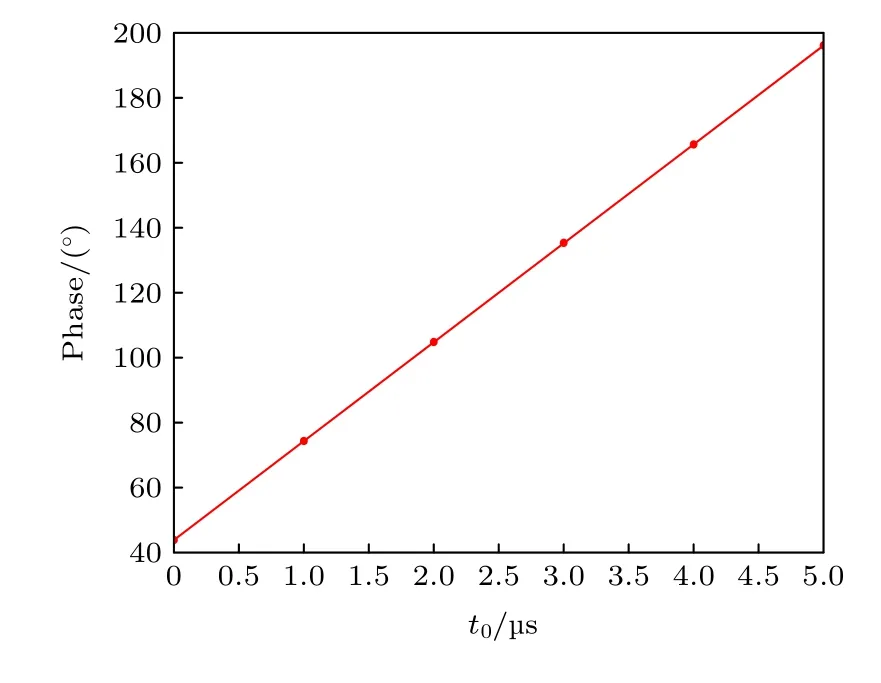
图5 系统延迟时间测量Fig.5.System delay time measurement.
利用半高宽的方法对弛豫时间进行测量,在X轴上施加约 50 nT的振荡磁场,通过改变施加磁场的频率得到响应曲线,同时以X轴最大响应频率的相位作为参考相位零点,对输出信号进行正交解调得到对应的吸收曲线如图6 所示.

图6 幅频特性测量曲线Fig.6.Amplitude-frequency curve measurement.
利用吸收曲线的半高宽估计法得到的弛豫时间为35.188 μs,而利用响应曲线估计的弛豫时间为36.001 μs.两种方法的测量结果存在小的差异,这是由于系统延迟时间导致不同频率的信号解调相位不同,因此测量得到的吸收曲线出现形变导致的.
再利用测量相位差的方法测量弛豫时间,由于实验上探测光轴的方向与磁场方向并不完全重合,这会导致相位的测量出现偏差.在实验中多次的调节探测光轴是较为复杂的,通过调节磁场的方向同样可以使两者共轴.通过不断改变磁场角度,分别测量不同角度下对应不同偏转角的相位变化,计算其对应的弛豫时间,从而画出弛豫时间估计值随偏转角变化的曲线如图7,在探测光角度不为0时,高频与低频的估计结果出现不同,但是在两轴方向相同的情况下,他们的估计结果趋于一致.在40 kHz,70 kHz,100 kHz下,测量得到的曲线在磁场角度φ=1.11°处相交,此时得到估计的弛豫时间为36.104 µs.

图7 探测光偏移角对弛豫时间测量的影响Fig.7.The influence of optical offset Angle on relaxation time measurement.
通过实验对比了几种方法在不同大小的振荡磁场下的测量结果如图8 所示,在很小的磁场下利用响应曲线估计(图中绿色方块)和相位估计的结果相近,与利用吸收曲线估计的结果有一定的差异.随着磁场强度的增大,利用响应曲线和吸收曲线的估计结果的误差增大,而利用相位测量的结果较为稳定.

图8 不同方法测量结果随磁场强度的变化Fig.8.Variation of measurement results with magnetic field intensity by different methods.
5 结论
本文研究了核磁共振陀螺仪中EPR 信号对振荡磁场响应的不对称性,这种不对称性会导致测量短弛豫时间的碱金属原子共振频率和强度时出现偏差,并从理论和实验上解释并验证了这种现象.利用不对称性,文中提出了通过改变磁场方向测量信号相位变化,从而测量系统的延迟时间以及Rb原子横向弛豫时间的方法,这一测量弛豫时间的方法在理论上具有更广的测量范围.同时对现有的利用幅频响应曲线估计弛豫时间的方法进行理论分析,探究了其准确性和鲁棒性,并给出了适用范围更广的经过理论修正的估计方法.在实验上通过施加特定的信号延迟,验证了这种测量系统延迟时间方法的可靠性.此外,通过测量87Rb 原子的横向弛豫时间,比较了利用响应曲线,吸收曲线以及相位差异这三种测量方法的区别.发现对于极短的弛豫时间,利用相位差异测量的方法具有更高的准确度,并且受到磁场变化以及系统传输延迟的影响更小.文中提到的测量方法有助于更精确的标定NMRG的各项参数,建立更为完善的模型,对通过建立闭环反馈以提高陀螺仪性能的研究有重要意义[24].

