超临界氮气在单壁碳纳米管内吸附行为的GCMC 模拟研究*
赵明慧 刘忠军† 姬帅 刘晨 敖庆波
1)(西安石油大学材料科学与工程学院,西安 710065)
2)(西北有色金属研究院,金属多孔材料国家重点实验室,西安 710016)
超临界流体技术发展日益成熟,开展超临界流体在纳米多孔材料内的吸附行为研究,对超临界流体技术的开发与应用推广具有理论意义和使用价值.本文利用巨正则蒙特卡罗法,主要模拟了超临界状态下氮气在单壁碳纳米管内的吸附行为.结果表明超临界条件下,氮气在单壁碳纳米管内的吸附等温线不严格遵循层状吸附机制;氮气吸附等温线出现峰值,且峰值随温度的升高而逐渐减小.与亚临界条件不同,超临界条件下流体局部密度分布曲线的吸附峰并不能代表过剩吸附量的增加,且本体气相密度对吸附过程产生的影响不可忽略.通过对超临界条件下的吸附积分摩尔焓进行研究,发现过剩积分摩尔焓随孔径增大而减小;吸附积分摩尔焓在较低压力下随孔径增大而减小,但在较高压力下随孔径的增大而增加.
1 引言
在热力学里,一种物质的固相、液相和气相共存时的温度和压力值称为三相点.除三相点外,每种稳定物质两相之间的相转变也都发生在固定的临界点(critical point),临界点条件包括临界温度、临界压力和临界密度.当气体或液体的压力和温度处于其临界点以上时,这种具有独特理化性质的非凝缩性流体状态称为超临界流体(supercritical fluid,SCF)[1].目前,关于超临界流体的理论日趋成熟,超临界流体技术发展迅速,已经深入到食品工业、有机化学、聚合物加工、环境治理以及生物工程等各方面,具有广阔的应用前景[2−5].
超临界流体技术中存在大量SCF 溶质在固体多孔材料上的吸/脱附现象,科学家们通常以实验与模拟相结合的方法从机理上开展多方位的深入研究.早在1997年,Gusev等[6]发现将超临界甲烷(308 K)在活性炭上的实验吸附等温线与GCMC模拟相结合,可有效地表征微孔PSD 以及准确地预测更高温度下的吸附.2000年Zhou等[7]测定了超临界条件下(233—333 K和0—10 MPa)甲烷在高表面活性炭上的吸附等温线,并利用Langmuir-Freundlich 方程参数评估吸附相中的分子间距离,发现本体气体和吸附相之间存在明显的界面.在近两年的研究中,Ansari等[8]提出了一种综合实验和建模的方法,可利用在亚临界以及超临界条件下获得的气体吸附数据来表征多孔碳材料.Pini等[9]对不同形态吸附剂的净吸附和过剩吸附等温线进行对比分析,指出过剩吸附与特定超临界吸附相的性质密切相关.Yang等[10]研究了纳米多孔煤中超临界CO2的吸附行为,对超临界CO2过剩吸附等温线进行了重建.Tan等[11]对超临界极性和非极性气体混合物的竞争与协同吸附行为进行了GCMC 模拟,研究发现超临界混合流体分子间的吸附行为表现类似于理想气体,吸附质间的相互作用可以忽略不计,并量化了亨利常数、等温线、能量和孔内密度分布等参数.
本文利用GCMC 模拟研究了超临界条件下温度、孔径对SWCNT 内氮气吸附行为的影响规律,并与亚临界(77.3 K)氮气吸附行为进行了对比分析;研究中使用积分摩尔焓代替等量吸附热对超临界吸附过程中的热化学性质进行表征,以期为超临界流体技术的应用研究与开发提供理论借鉴.
2 势能模型与模拟详情
模拟采用无限长圆柱孔模型,取SWCNT 孔长为4 倍孔半径,在孔模型两端应用周期性边界条件.为了提高计算效率,采用的氮气分子模型为1C-LJ N2模型[12],将氮气分子看做单个LJ 流体颗粒,分子内部不存在键长或键角的变化.模拟程序中设定NSite=1,即只有一个分散位,氮气分子模型的结构不会发生改变,且超临界温度下氮气稳定存在.氮气分子间势能由LJ 势能模型[13]计算:

式中,r为两个分子间距离;εff为分子间势能阱深;σff为碰撞直径(εff为零时的分子间距离).每个氮气分子与SWCNT 间的液-固势能则采用Steel 模型计算[14],图1为Steel 模型示意图,其液-固势能表达形式

式中,

其中ρs为固体单位面积原子个数(m–2);ri指流体分子i到圆柱孔中心的距离(见图1);R为圆柱孔半径;σsf和εsf为固体分子与流体分子间综合碰撞直径和综合势能阱深,均满足Lorentz-Berthelot(LB)混合规则:F[a;b;c;d]为高斯超几何函数.本文在进行氮气吸附模拟计算时,N2所对应的LJ 势能参数[12]为:εff/kB=101.5 K,σff=0.3615 nm;SWCNT 模型中C 原子的LJ 势能参数[15]为:εss/kB=28.0 K,σss=0.34 nm;其中kB指玻尔兹曼常数(1.38066×10–23J/K).

图1 流体分子与圆柱孔的相对位置图Fig.1.Schematic diagram of fluid molecules and cylindrical pore.
GCMC 模拟平衡和数据采样阶段均为100000次循环,为了保证实现平衡,每次循环中执行三种概率相等的分子扰动:分子的空间移动、插入和删除操作,共1000 次.
由于普通意义上的吸附热定义存在限制,超临界条件下过剩吸附量达到极大值时,等量吸附热会出现没有物理意义的奇点.为了便于分析吸附过程的相关机理,利用积分摩尔焓替代等量吸附热以表征吸附过程中的能量变化.单位压力P改变引起系统焓变∂Htot/∂P的变化方程[16,17]为

该方程不存在奇点,也称为吸附微分摩尔焓.其中T指温度,VG为主体流体体积,U为模拟系统的构型能,函数f统一定义为f(X,Y)=〈XY〉−〈X〉〈Y〉,〈〉表示系统平均值.N和NG分别为可进入孔体积[18,19]相同的模拟盒子中吸附相和主体相的分子个数.若已知压力P所对应的吸附系统量N,则以波动自变量进行计算系统积分摩尔焓的公式为

式中,ρG为主体流体密度.若相应的系统过剩吸附量为Nex,则吸附积分摩尔焓定义为

对此式进行修正,得到基于过剩吸附量的积分焓变与过剩吸附量的变化方程式:
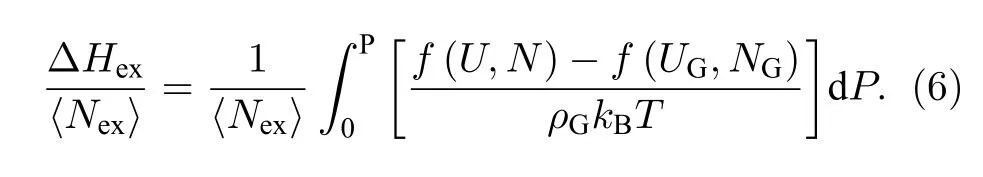
3 结果与讨论
3.1 吸附等温线
对亚临界以及超临界条件下孔半径为1.83 nm的SWCNT 进行氮气吸附模拟,图2(a)给出了氮气在77.3 K 以及从临界点(126 K)附近到超临界温度下的氮气吸附等温线(100—400 K).从图2(a)可以看出,当温度为77.3 K时,吸附过程中过剩吸附量随压力的增大而增加,吸附等温线具有较明显的台阶,整体呈阶梯状上升直至达到饱和吸附,吸附过程遵循层状吸附机制.此外,在13 kPa 压力时,吸附量突增,说明发生了气-液相变,即出现毛细凝聚现象.随着温度逐步升高直至超临界温度,可以明显地看出,吸附等温线的阶梯特性愈发不明显,吸附过程不再严格遵循层状吸附机制.与亚临界氮气吸附不同,超临界温度下吸附初始阶段,本体气相密度较小,对过剩吸附量产生的影响较小,然而随着压力的增大,本体气相密度占比增加,导致吸附等温线先呈上升趋势随后再下降,在一临界压力值下出现峰值,且随温度的升高,此吸附峰值逐渐减小,达到峰值时的临界压力值增大,吸附量尖峰逐渐平缓.超临界状态下本体气相密度随压力变化情况见图2(b).
有趣的是,在临界点温度附近(100和126 K),过剩吸附量在达到峰值后分别在1400和3000 kPa处骤降,这是由于此时压力的微小改变会引起本体气相密度的极大波动[20],当压力达到临界值时,本体气相密度急剧增加,从而导致过剩吸附孔密度减小,吸附量骤降.
从图2(a)中还可以看出,在超临界状态下,不同温度的吸附等温线在较高压力处相互交叉,过剩吸附量对本体气相密度较敏感.为了更清晰地分析其中的变化规律,以过剩吸附量与本体气体密度之间的变化关系对超临界状态下的吸附等温线进行表征,如图3 所示,这种表征方法可以更准确直观地反映出温度对吸附过程的影响.结果与图2(a)一致,过剩吸附量存在峰值,峰值随温度的升高而降低,吸附峰逐渐平缓甚至消失.整体而言,在相同的气体密度下,过剩吸附量随温度的升高而减小.

图2 (a)不同温度下(77.3,100,126,150,200,250,300和400 K)SWCNT(R =1.831 nm)内的氮气吸附等温线;(b)超临界状态下本体气相密度随压力变化曲线Fig.2.(a)Adsorption isotherms of N2 in SWCNT(R =1.831 nm)at different temperatures(77.3,100,126,150,200,250,300 and 400 K);(b)variation curve of bulk gas density with pressure under supercritical conditions.

图3 氮气过剩吸附量随本体气相密度的变化曲线Fig.3.Isotherms of nitrogen adsorption in terms of excess adsorption capacity versus gas bulk gas density.
3.2 局部密度分布
为了深入理解SWCNT 内氮气在亚临界与超临界状态下的吸附过程,本节选取具有代表性的77.3和300 K 两个温度下的氮气吸附行为进行对比研究,并根据氮气分子在SWCNT 内的局部密度分布以及微观排列分布情况具体分析了两者之间的异同.
图4 给出了77和300 K 温度下孔半径方向上(自SWCNT 内壁至孔中心)局部密度随压力的变化情况,图中一个峰值代表一层流体层,相应地,图5 给出了两个温度下氮气分子在特殊压力点所对应的瞬间构型,图5(a)中A,B,C和D 四个瞬间构型分别对应于图2 中的特殊压力标示点.从图4(a)中可以看出,77.3 K 温度下存在明显的吸附峰,各吸附峰的位置不随压力的变化而变化,这再次说明了氮气在单壁碳纳米管内严格遵循层状吸附转变机制.另外,每个吸附峰的峰值随压力增大而升高,前两个吸附峰表现更为明显,这说明整个吸附过程中SWCNT 内流体层的密度随压力增大而不断升高,分子排列逐渐紧凑形成致密层.结合图5(a)进行分析,可知由于受液-固势能的影响,氮气分子首先沿着单壁碳纳米管内壁形成第一层,随着压力的升高形成第二层流体层,继而压力逐渐升高形成更高的吸附层并发生凝聚相变(由C 到D),这与图4(a)中较高压力下孔中心附近突然出现新的吸附峰相对应.
在300 K 温度下(图4(b)),整体局部密度分布值较低,氮气吸附过程不再严格遵循层状吸附机制.较低压力下(1和3 MPa),氮气分子已经随机充斥在碳纳米管内部任何位置(见图5(b)),这是由于高温下吸附系统熵值增加,使流体分子具有较高的能量,在吸附过程中流体分子的自由活动度变大,热运动增加,更容易在不同分子层之间穿插跳跃.当压力增大时,氮气分子持续填充,但分子间的距离较大,与亚临界条件下相比吸附量较少.

图4 孔半径方向上LJ 局部密度分布与压力关系(a)77.3 K;(b)300 KFig.4.LJ local density distribution versus the pressure in pore radii direction:(a)77.3 K;(b)300 K.
为了更详细地定量研究氮气的吸附过程,图6给出了氮气分子在77.3和300 K 温度下特殊压力点时的二维局部密度分布,图6(a)中曲线A,B,C和D 分别对应图2(a)中的标示点.与图5(a)相对应,在压力点A 沿管壁形成单层流体层,压力点B 时开始形成第二层流体层,且流体层的密度峰值随着压力升高不断增加,压力点C 形成三层流体层,到点D 时突然吸附峰增多,即孔内部瞬间被氮气分子填满,发生凝聚相变,这与前文分析结果一致.

图5 SWCNT 内氮气吸附过程瞬间构型图(a)77.3 K 温度下,压力分别为0.04,3,13和15 kPa 时氮气分子的瞬间构型,压力点分别对应于图2 中标示点A,B,C和D;(b)300 K 温度下,压力分别为1,3,18和100 MPa 时氮气分子的瞬间构型Fig.5.The snapshots of N2 adsorption process in SWCNT:(a)N2 molecules at the temperature of 77.3 K,and the pressure points correspond to the marked points A,B,C and D in the Fig.2;(b)N2 molecules at the temperature of 300 K under the pressure of 1,3,18 and 100 MPa,respectively.

图6 77.3(a)和300 K(b)温度下孔径方向上特殊压力点下的局部密度分布.图(a)中A,B,C和D 分别对应于图2 中的标示压力点;图(b)中平行虚线为对应压力下本体流体气相密度Fig.6.Local density distribution at special pressure points in the pore radii direction at 77.3(a)and 300 K(b);A,B,C and D in Figure(a)correspond to the marked pressure points in the Fig.2 respectively;the dash-dotted horizontal line in Figure(b)refers to the bulk gas density at the corresponding pressure.
图6(b)为超临界状态下不同压力点对应的局部密度分布,依然可见明显的吸附峰.在1 MPa时,局部密度分布仅存在一个峰值,并且任一位置的局部密度均大于其对应压力下本体流体的气相密度,当压力增加至18 MPa时,第一个吸附峰谷略低于本体气相密度时,此时对应于图2 中吸附量出现峰值,而压力继续增加超过这一临界压力值达到100 MPa时,局部密度出现三个峰值,且峰值更高.局部密度分布曲线在气相密度上下震荡变化,部分位置的密度值小于气相密度;本体气相密度进一步增大,从而对过剩孔密度产生影响,导致过剩吸附量减小,这说明超临界状态下,局部密度分布曲线的吸附峰并不能代表过剩吸附量的增加.而在亚临界条件下,压力为15 kPa 时(D 点),本体气相密度为0.00067(无量纲),远远小于其局部密度分布,就亚临界的整个吸附过程而言气相密度较小,所以亚临界条件下本体气相密度对吸附过程所产生的影响可以忽略不记.
在300 K 温度下,当压力增加至临界值(18 MPa)时,局部密度分布曲线存在两个吸附峰,且两个峰值之间的最小值略小于本体气相密度,在此临界压力之前,任何位置的局部密度分布曲线值均在本体气相密度之上,为了进一步证实超临界状态中存在这种现象,图7 给出了200和400 K 温度下的局部密度分布曲线与相对应压力下气相密度的对比关系.与图2 中相对应,在这两种温度下当压力分别增加至8和40 MPa时,吸附量均达到峰值,此时局部密度分布曲线前两个峰值之间的最小值均略微小于气相密度,压力进一步增大时,局部密度分布曲线在气相密度周围上下震荡变化,这与300 K 温度下的现象一致,充分说明了对于超临界氮气吸附,当局部密度分布曲线的最小值开始表现为低于本体气相密度时,过剩吸附量达到最大值.

图7 200(a)和400 K(b)时氮气在SWCNT 内孔径方向上的局部密度分布曲线,平行虚线为对应压力下本体流体气相密度Fig.7.Local density distribution curve of N2 in the pore radii direction of SWCNT at 200(a)and 400 K(b),the dash-dotted horizontal line refers to the bulk gas density at the corresponding pressure.
3.3 层压缩性
层压缩性[16]是表征不同流体层内的分子排列紧密程度、深入研究不同吸附层之间差异的一种方式,其计算公式为

式中,Ni为第i层内的分子数;〈ρi〉为第i层的局部密度.
图8 给出了77.3和300 K 温度下氮气吸附过程中层压缩性与压力之间的关系.从图8 可以看出,随着压力的增大,层压缩性均减小,不同的是在超临界状态下层压缩性与压力的双对数曲线呈线性减小关系,这说明超临界状态下限域空间内的各吸附层之间没有边界,当压力增大时,所有氮气分子同时发生致密化.另一方面,受液-固势能的影响,紧挨管内壁的第一层内分子数较多,致密度大,从而导致第一层流体层压缩性最小.

图8 77.3(a)和300 K(b)温度下层压缩性和压力的变化关系对数曲线,图中对应于右边Y 轴的点划线为相应温度下的吸附等温线Fig.8.The layer compressibility versus pressure logarithmic curve at 77.3(a)and 300 K(b),and the Dash-dotted line corresponding to the right Y axis is the adsorption isotherm at the corresponding temperature.
与之相比,在亚临界条件下,流体层分子热运动较小,排列较紧密,分子间平均距离较小,其液-固和液-液势能对吸附过程的影响更大,致使亚临界条件下的第一层可压缩性相比超临界状态下的第一层压缩性较小,并且亚临界条件下第一层与第二层之间的压缩性在低压时相差较大.另外在77.3 K 温度下,当基本完成第一层和第二层流体层填充时,两层所对应的压缩性值近似(图8(a)中红色标示点),当压力到达13 kPa时,吸附等温线骤增,而第三层流体层的压缩性骤降,第一与第二流体层压缩性也均有所下降,再次说明此时孔内部氮气分子间距离迅速减小,发生了凝聚相变.
图9 给出了亚临界和超临界状态下氮气在单壁碳纳米管内的积分摩尔焓与压力的变化关系,红色实线为系统积分摩尔焓(− ∆HTOT/NTOT),灰色实心圆图标为吸附积分摩尔焓(− ∆HTOT/Nex),蓝色实心圆图标为过剩积分摩尔焓(− ∆Hex/Nex),虚线为等量吸附热,与右边Y轴对应的绿色点划线为相应温度下的过剩吸附等温线.从图9 可以看出,在77.3 K 温度时,所有积分摩尔焓与吸附热数量级相同,由于气相可视为理想气体,密度较低,且其摩尔焓值不变,系统中的总分子数主要由吸附相分子构成,所以系统积分摩尔焓与吸附积分摩尔焓相同,在发生毛细凝聚(13 kPa)时,吸附系统内氮气分子数骤增,系统中吸附积分摩尔焓和过剩积分摩尔焓均急剧下降.

图9 氮气在77.3,150,300和400 K 时在SWCNT 内吸附的积分摩尔焓,灰色虚线为等量吸附热,绿色点划线与右边Y 轴对应为相对应温度下的过剩吸附量Fig.9.Integral molar enthalpy of nitrogen adsorption in SWCNT at 77.3,150,300 and 400 K,The gray dotted line indicates the Isosteric heat of adsorption,and the green dash-dotted line corresponding to the right Y axis is the adsorption isotherm at the corresponding temperature.
超临界条件下(150,300,400 K)等量吸附热在过剩吸附量达到峰值时出现奇点,而积分摩尔焓曲线均无奇点存在.由于超临界系统中存在的气相不可忽略,导致过剩积分摩尔焓与吸附积分摩尔焓之间出现差值,且温度升高会导致本体气相占系统分子数总量的比重增大,所以在临界压力前此差值亦随温度的升高而增大.在较高压力下,系统积分摩尔焓减小,系统内气相分子数量大幅度增加,过剩吸附量开始随着压力的增加而减少,从而导致吸附积分摩尔焓和过剩积分摩尔焓增加.另外,可以看出在150 K 温度下,过剩吸附等温线的峰度较陡,吸附积分摩尔焓与过剩积分摩尔焓在临界压力值下同时出现向下的拐点,造成此现象的原因是此时过剩吸附量出现骤增,然而超过临界压力点后,过剩吸附量开始减小,吸附积分摩尔焓与过剩积分摩尔焓开始表现为不同幅度的增加,且温度较低的吸附系统具有较高吸附积分摩尔焓与过剩积分摩尔焓.
3.4 孔径对吸附过程的影响
图10 给出了77.3和150 K 温度下氮气在不同孔径(R=0.7464,1.153,1.56和2 nm)SWCNT内的吸附等温线.从图10 可以看出,在77.3 K 温度下,氮气在较大孔径SWCNT 内依然遵循层状吸附机制,并且发生毛细凝聚的压力值随着孔径的增大而增加.在超临界状态下,受吸附势能的影响,过剩吸附量随孔径增大而减小,过剩吸附等温线均出现峰值,且出现峰值的临界压力值Pm随孔径增大而增大,过剩吸附量在峰值之后随着压力的增大而减小,最终趋于常数.

图10 77.3和150 K 时氮气在R =0.7464,1.153,1.56和2 nm SWCNT 内的吸附等温线Fig.10.Adsorption isotherms of N2 in R=0.7464,1.153,1.56 and 2 nm SWCNT at 77.3 and 150 K.
图11(a)为77.3 K 温度下氮气在不同孔径(R=0.7464,1.153,1.56和2 nm)SWCNT 内基于过剩吸附量的等量吸附热.由于较小孔内具有较高的液-固势能,因此受液-固势能的影响,初始等量吸附热与第一层吸附层形成后的等量吸附热均随着孔径增大而减小.在较大孔径(R=1.153,1.56和2 nm)SWCNT 内达到饱和吸附时的等量吸附热则相差不大(灰色圆部分),这是因为在完成凝聚相变后,孔内均已形成完整、致密的流体层,三者的过剩孔密度相近,每个氮气分子周围的临近分子数目几乎相同.值得注意的是,在孔半径为1.153和1.56 nm的SWCNT 内氮气形成第一层流体层后,等量吸附热出现了热峰(红色圈部分).这是由于在第二吸附层形成初期,新进入的个别氮气分子受固-液与液-液相互作用影响,被挤入密度较高的第一吸附层内,导致第一吸附层的凝聚相发生了液-固相变,从而等量吸附热出现热峰.相关研究表明这种热峰的出现取决于吸附质的性质和吸附温度[21].
从图11(b)中可以看出,超临界状态下(150 K),由于小孔中具有相对较强的势场,基于过剩吸附量的过剩积分摩尔焓(− ∆Hex/Nex)随孔径增大而减小,对于吸附积分摩尔焓(− ∆HTOT/Nex),当压力小于Pm(过剩吸附量出现极大值时的压力)时,其也随孔径增大而减小.然而当压力大于Pm时,过剩吸附量减小,导致吸附积分摩尔焓反而随孔径增大而增加,这与SWCNT-Ar 吸附体系中所得结果一致[22].对于SWCNT-N2吸附体系,在较小孔径SWCNT内,当压力大于其Pm时,吸附积分摩尔焓以较高的增长速率呈上升趋势,较大孔径SWCNT内吸附积分摩尔焓的增长速率则较慢.这充分说明了较大孔径单壁碳纳米管内气相流体占比增加幅度更高,气相流体在较大孔内对吸附积分摩尔焓产生的影响更大.因此可得出结论:超临界条件下,较大孔径SWCNT 内的氮气吸附焓变对气相流体更敏感.

图11 (a)77 K 温度下氮气在不同孔径SWCNT 内的等量吸附热随过剩吸附量的变化关系;(b)150 K 温度下过剩积分摩尔焓随压力的变化关系曲线,插入图为吸附积分摩尔焓随压力的变化关系Fig.11.(a)Isosteric heat of N2 adsorption versus excess adsorption at 77 K,in SWCNTs with different radii 0.7464,1.153,1.56,2 nm;(b)the integral molar enthalpy versus pressure at 150 K,and the insertion diagram shows the variation relationship of adsorption integral molar enthalpy with pressure.
4 结论
本文对比研究了超临界和亚临界条件下氮气在单壁碳纳米管内的吸附行为,并对不同吸附系统中的等量吸附热及积分摩尔焓变进行了讨论.通过对比分析发现:
1)在超临界条件下,由于分子热运动增加,自由活动度变高,更容易在不同分子层之间穿插跳跃,导致氮气在单壁碳纳米管内的吸附等温线不严格遵循层状吸附机制.吸附等温线在临界压力下会出现峰值,随温度的升高该峰值逐渐减小,且达到峰值时的临界压力值增大,吸附量尖峰逐渐平缓.另外,在临界点温度(126 K)附近,压力的微小改变会引起本体气相密度的极大波动,导致吸附等温线在出现峰值后出现骤降现象.
2)与亚临界条件下不同,超临界吸附条件下氮气在碳纳米管内的本体气相密度较大,其对过剩孔密度产生的影响不可忽略,且超临界条件下局部密度分布曲线的吸附峰并不能代表过剩吸附量的增加.
3)超临界状态下本体气相会对超临界积分摩尔焓变产生影响,导致吸附积分摩尔焓与过剩积分摩尔焓之间出现差值,且此差值随着温度的升高而增大.通过研究孔径对吸附过程的影响发现基于过剩吸附量的过剩积分摩尔焓随着孔径的增大而减小.吸附积分摩尔焓在较低压力下随着孔径增大而减小,但在较高压力下大孔径单壁碳纳米管内气相流体占比增加,导致吸附积分摩尔焓随孔径的增大而增加.

