基于准粒子模型的原生磁星研究*
王谊农 初鹏程 姜瑶瑶 庞晓迪 王圣博 李培新
(青岛理工大学理学院,青岛 266033)
研究了奇异夸克物质在零温、有限温度、强磁场下基于准粒子模型的热力学性质.结果说明夸克物质的对称能会随着准粒子模型的耦合常数增加而增加,对称能越大夸克物质的物态方程就越硬;结果还表明温度场与磁场对奇异夸克物质的每核子能量、每核子自由能、各向异性压强都有较大影响.通过对原生磁星的计算,发现原生磁星的最大质量和核心温度不仅受到原生星演化过程中的加热过程影响,还与磁星内部磁场强度与磁场方向的分布密切相关.随后考虑了磁星内部径向、横向磁场混合的情况,发现磁星最大质量会随着磁场方向与径向的夹角变化.本文所做工作对于理解有限温度、强磁场下奇异夸克物质的同位旋效应和热力学性质以及致密星体物理中的原生磁星的性质具有一定的推进作用,为接下来寻找磁星内部的真实磁场分布提供了前期理论基础.
1 引言
研究强相互作用物质的热力学性质是核物理、宇宙学、粒子物理等前沿的重要基础问题之一[1–4],其物态方程的求解对于理解核反应与核结构、致密星体物理、早期宇宙的物质形态等前沿物理领域具有重要的作用.在地球实验室,重离子碰撞实验是探索强相互作用物质的重要手段,如相对论重离子碰撞实验(RHIC)、大型强子碰撞实验(LHC)等已经能够揭示低密、高密、高温的强相互作用物质的性质;在自然界中,中子星的相关实验观测结果则为人们探索高密、低温的强相互作用物质提供另一种途径.在致密星体工作中,星体内部奇异夸克物质能否出现是热点问题—如果奇异夸克物质在中子星物质中占比增加,那么人们可以进一步研究由奇异夸克物质构成的(奇异)夸克星,而夸克星的存在可能性仍为现代核物理和天体物理的未解重要课题,不能够被排除[5–11].构成夸克星的奇异夸克物质是由退禁闭的u,d,s 三味夸克以及轻子通过β平衡组成的[12–16],一般来说奇异夸克的加入会增加自由度,进而使得物态方程变软,所以通常很难用合理的夸克模型来描述实验观测得到的大质量致密星体为夸克星.然而经过尝试,科研工作者也可以通过考虑手摆增加袋常数、同位旋相关势能或有效质量、有效质量密度相关等方法得到较大质量夸克星[17–26].在最近的实验探测中,大质量脉冲星结果多次出现:2013 年观测的PSR J0348+0432 脉冲星的质量为(2.01±0.04)M⊙[27],是当时精确探测的大质量脉冲星之一;2018 年观测的脉冲星PSR J 2215+5135的质量更大,达到了[28].在文献[29]中,人们通过相对论引力时间延迟效应得到的脉冲星MSR J0740+6620的最大质量达到了(68.3% 置信度)、(95.4% 置信度).最新LIGO/Virgo 合作组观测到的双致密天体并合事件GW190814[30]的“次星”m2质量能达到 2.50M⊙−2.67M⊙(90%置信度).如此大质量的致密天体如果候选者是夸克星,会对奇异夸克物质的物态方程等热力学性质有着更强的约束,对夸克物质的唯象模型也有了更高的要求.此外,对于大质量中子星的情况还存在着其他的解释,比如其他的星体模型或者大质量中子星的质量可能与其伴星的质量和金属丰度相关等[31].目前发现的大质量中子星几乎都位于高质量 X 射线双星双星系统(HMXB)之中,这预示大质量中子星质量可能与双星系统中的伴星质量、金属丰度和对流超射系数正相关[32].
原生星通常认为发生在超新星爆发后,此时星体已经耗光了能源补给,可能会被引力压缩而形成致密星体或者是黑洞,具体成因与坍缩的具体初始条件有关[33].对于从原生中子星到原生夸克星的相变,人们知之甚少,因为在星体燃烧过程中核子夸克相变的复杂性相对较高.之前的相关工作表明[10,34–40],奇异夸克星有可能来自中子星的并合,也可以用星体演化中的不同等熵阶段去描述奇异夸克星的质量、半径等性质.这对于解释原生星的加热、冷却过程以及有限温度下夸克星物质的热力学性质具有非常重要的意义.
据估算,致密星体表面磁场B接近 1014G[41–43],内部可能会增加至 1018G[44]到1020G[45].如此巨大的内部磁场,会使得致密星体物质的空间旋转对称性破却,压强会各向异性[45–48].沿着磁场方向的压强(纵向压强)经过计算一般会小于垂直于磁场方向的压强(横向压强).在描述磁星内部磁场强度分布的时候,人们通常采用密度相关磁场[49–54],所以如何去探索磁星内部磁场强度与方向分布对磁星物质的热力学性质(尤其是物态方程)的影响是磁星研究的重点,对于核物理、天体物理具有非常重要的作用.如果考虑得更深入,在研究磁星的性质中考虑原生星的演化曲线上的不同的等熵阶段,可以求解原生磁星的性质.原生磁星是一类转动周期为毫秒量级的具有超强的磁场(B >1018G)、超高温度(T >1010K)的原生致密星体,其与依靠磁场供能的可被观测的“磁星候选体”(软伽马重复爆和反常X 射线脉冲星这两类源可统一被称为“磁星候选体”)有着一定的差异性,可以作为唯象的理论模型解释快速射电暴以及伽马射电暴的起源问题[55].较高的X-射线光度和频繁的外爆是由磁星内部超强磁场的衰变提供能量来源及动力,由磁偶极辐射模型推导出的表面磁场可达到1013—1015G,内部磁场可能更高.时至今日,磁星模型已经发展到了相当的规模,为软伽马重复爆和反常X-射线脉冲星在高能段多样性观测现象提供了令人满意的解释[56–58].故磁星的性质与快速射电暴以及伽马射电暴的研究密不可分,考虑到在不同等熵阶段中温度场会对磁星物质有非常大的影响,最终星体演化中的加热、冷却阶段可能会影响到磁星的质量与半径等相关性质,这是我们研究的重点内容.
本文安排如下:首先基于准粒子模型介绍零温、有限温度、强磁场下奇异夸克物质的热力学量的推导,并给出奇异夸克物质需满足的电中性、重子数守恒、β 平衡等条件;其次通过计算与画图,详细讨论零温、有限温度、强磁场下奇异夸克物质的热力学性质;最后利用TOV 方程求解原生星与磁星的相关性质,并给出结论.
2 前期推导工作
2.1 准粒子模型理论推导
与常用的夸克物质的唯象模型(比如质量密度相关模型)不同,准粒子模型的提出不是建立在把夸克与夸克、夸克与介质之间的相互作用包含在重子数密度相关的 有效质量中[59–79],而是来自硬密环的单圈自能近似得到的色散关系的零动量极限结果,具体表达式如下[80–82]:
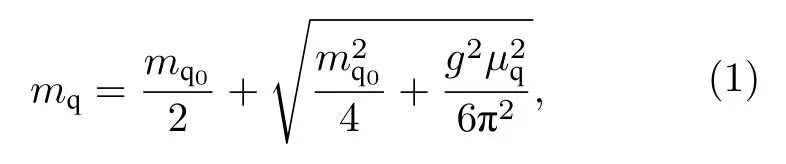
这里mq0是夸克的裸质量,设u,d,s 三味夸克的裸 质量分别为mu0=5.5 MeV,md0=5.5 MeV,ms0=95 MeV.µq代表着第i味夸克的化学势,g是强相互作用的耦合常数,这里设为可调参数.需注意的是,g作为强相互作用耦合常数,原则上需要随着温度场与磁场进行跑动,这对于更清楚地理解温度场与强磁场下的工作更有意义,由于计算上与定义上存在一定的困难,我们将在之后的工作中对强耦合常数进行更加深入的讨论.
于是奇异夸克物质的总热力学势密度可以写为

这里Bi(µi)是准粒子模型中有效质量项化学势相关所产生的附加项,B是提供夸克禁闭的可调参数,Ωi则代表奇异夸克物质中的每味夸克、轻子对应的热力学势密度,在有限温度与强磁场情况下其表达式可写为

式中pz是z方向动量,Bi(µi)的积分形式可写为

这里需要注意的是,Bi这个参数产生的原因是由于准粒子模型中夸克的有效质量与化学势相关所自洽求解得到的附加项,正是由于此项在热力学势密度中的参与,才使得最终基于准粒子模型的推导满足不依赖于参数空间的热力学自洽.
夸克与轻子的粒子数密度的表达式为

自由能密度F可以通过热力学关系求出,注意最后一项来自于磁场:

由于外加强磁场,磁场对能量的贡献B2/2 需要考虑.致密星体内部也存在着强磁场,其表面的磁场B可能高达 1014G[41–43];而星体内部的磁场则可能会增加到 1018G[44].在之前的磁场工作中[45],夸克星核心的磁场甚至可能高达 1020G.如此强的磁场会破坏空间旋转对称性(O(3)),进而使得奇异夸克物质的压强发生劈裂[45–48].劈裂后的各向异性压强可以定义为平行于磁场方向的纵向压强P∥以及垂直于磁场方向的横向压强P⊥,相应的表达式可以写为[45]

这里M是系统的磁化率,具体表达式为

通过(10)式可见,纵向压强在强磁场情况下比横向压强的取值低,而且纵向压强P//可以满足Hugenholtz-Van Hove 定理,体现了热力学自洽性.对于能量密度εi,其表达式可以写为

有限温度情况下的奇异夸克物质的熵的表达式可写为

接下来可以通过求解有限温度、强磁场下奇异夸克物质的热力学性质进而求解夸克星的性质.
2.2 奇异夸克物质
奇异夸克物质是由u,d,s 三味夸克以及轻子(e,µ,νl等)通过电中性条件构成.在确定了重子数密度之后,各种粒子需要满足β 平衡条件:

对于有限温度情况,需要考虑中微子,故β 平衡条件为

奇异夸克物质的电中性条件为

需要注意的是零温情况下µ子的产生需要电子的化学势达到µ子的质量才可发生,对于s 夸克,由于低密度处d 夸克的化学势较低,可能会在重子数密度较低时组分为零.
接下来采用准粒子模型分别计算不同情况下的奇异夸克物质的热力学性质.
3 奇异夸克物质性质计算结果
在核物理学家的普遍认知中,奇异夸克物质有可能是最稳定的物质形态,其满足所谓的绝对稳定条件[9],也就是说零温情况下的奇异夸克物质的每核子能量应该低于自然界最稳定核素M(56Fe)的每核子能量930 MeV;而在实验室与自然界中,从正常核物质到只有u,d 两味夸克构成的纯u-d夸克物质的相变并没有观测到,故绝对稳定条件还要求纯u-d 夸克物质的每核子能量最低点要高于930 MeV.考虑绝对稳定条件会进一步约束唯象夸克模型的参数空间,对唯象夸克模型提出了挑战.由于奇异夸克的加入会使得夸克物质物态方程变软,可能会很难描述大质量致密星体.近年来人们通常利用引入有效袋常数、增加矢量道耦合常数等方法,这些方法可以描述较大质量的夸克星,其中的考虑夸克物质的同位旋性质、通过调节夸克物质对称能来给出较硬的物态方程的方法得到了越来越多的关注[17–26].和核物质的对称能定义相似,夸克物质的对称能是将夸克物质的每核子能量对不对称度δ进行泰勒展开,二阶项系数Esym即为夸克物质对称能,相应结果如下:

其中,E0(nB,ns)=E(nB,δ=0,ns)是三味 u-d-s 夸克物质中考虑u 夸克和d 夸克组分相等的情况(通常称之为对称夸克物质),夸克物质的对称能Esym(nB,ns)可以写为

图1 描述的是基于准粒子模型的夸克物质对称能基于不同的参数随重子数密度的变化.这里选取四套参数,分别是g-2(g=2,B1/4=141 MeV),g-3(g=3, B1/4=136 MeV),g-4(g=4, B1/4=131 MeV)和g-5(g=5, B1/4=120 MeV).在我们之前的工作[83–86]中,利用此四套参数 计算了不同情况下的夸克星,其中在零温情况下分别描述了PSR J0348+0432(质量为(2.01±0.04)M⊙[27]),MSR J0740+6620(质量为),PSR J2215+5135(质量为[28]),及GW190814引力波并合事件中的可能为中子星的致密天体(质量为2.50M⊙—2.67M⊙[30])为夸克星,所以选取这四套参数研究基于准粒子模型下的零温夸克物质对称能.从图1 可以看出,对于所有的参数情况,夸克物质的对称能都会随着重子数密度的增加而增加.取值越大的对称能同位旋效应越强,通常可使得夸克物质的物态方程变硬,进而能够描述更大质量的夸克星.对比[83]夸克星最大质量结果,可直接给出基于准粒子模型较高的对称能能够支持大质量致密星体的结论.

图1 基于不同参数的夸克物质对称能Fig.1.Quark matter symmetry energy with different parameter sets.
图2 给出了零温、有限温度、强磁场下奇异夸克物质的每核子自由能/能量、压强随重子数密度的变化,这里选择了g-2 这套参数.图2 中对于有限温度情况选取T=50 MeV、磁场情况选取B=2×1018G,经过计算在温度大于50 MeV的时候温度场效应特别明显;磁场在高于B=2×1018G时,零温磁场的朗道能级上限变化所引起的“振荡”以及压强劈裂会更清楚.从图2 可以发现,在零温情况,奇异夸克物质的每核子能量最低点低于 930 MeV,满足了绝对稳定条件;其次在有限温度情况时,奇异夸克物质的每核子自由能与每核子能量的取值不再相等(有限温度情况下,自由能与能量表达式中的 T S0),故可以发现,考虑有限温度时每核子自由能/能量会随着温度的增加而降低/升高,出现了明显的温度相关的劈裂.在考虑零温有磁场的情况时,发现当磁场提升至B=2×1018G时,压强出现了明显的各向异性,平行于磁场方向的纵向压强P//与垂直于磁场方向的横向压强P⊥之间出现了随磁场增加的劈裂.零温情况强磁场下,每核子能量的最低点和纵向压强的零压点重合,体现了热力学自洽;在有限温度情况强磁场下每核子自由能最低点和纵向压强的零压点也重合,相应的零压点所对应的重子数密度会随着温度的上升而降低,随着磁场的增加而增加.从图2 还可以看出,在相同的重子数密度(如nB=1.5 fm−3)时,奇异夸克物质的压强会随着温度的增加而增加(在零磁场下、温度从0 提升到50 MeV时,压强从 508.2 MeV·fm−3升高到550.3 MeV·fm−3;当B=2×1018G、温度从0 提升到50 MeV时,横向压强从 607.7 MeV·fm−3升高到 650.3 MeV·fm−3).

图2 零温、有限温度、强磁场下奇异夸克物质的每核子自由能/能量、压强随重子数密度的变化Fig.2.The energy per baryon,free energy per baryon,and the corresponding pressure as functions of baryon density with g-2 in zero temperature,finite temperature,and strong magnetic field cases.
图3 给出了零温、有限温度、强磁场下奇异夸克物质的组分随重子数密度与固定重子数密度随磁场的变化.从左边的两栏可以发现,在零温无磁场和有磁场且B=2×1018G的情况中,g-2 这套参数描述的u,d,s 三味夸克的组分会随着重子数的增加显著变化:在低密处,由于d 夸克的化学势不够大,s 夸克的粒子数密度较低,由电中性条件可知d 夸克的粒子数密度接近两倍的u 夸克粒子数密度;随着重子数密度增加,s 夸克化学势增加使其粒子数密度增大,由电中性条件可令d 夸克组分降低,最终在较高密度处三味夸克的组分接近.对于温度较高的情况(如T=100 MeV),可以发现在低密处三味夸克的粒子数密度就已经较为接近了.由于高磁场情况朗道能级的上限降低,故可以在T=0,B=2×1018G 情况中观测到三味夸克的组分都发生了朗道能级变化而引起的“振荡”,而此现象在高温度情况T=100 MeV,B=2×1018G 时基本消失,这说明温度场会减弱奇异夸克物质中强磁场的效应.为了能更好地看出强磁场与温度场对夸克物质组分的影响,图3 最右边的一栏绘制了固定重子数密度nB=0.8 fm−3时三味夸克的组分在T=0与T=50 MeV 情况中随着磁场的变化,发现零温情况下,当磁场大于 2×1018G时,振荡效应明显增加;经过调试参数,考虑当温度恰好刚刚大于50 MeV时,磁场引起的振荡会随着温度的增加而基本消失,此结果更清楚地体现了温度场对磁场效应的减弱效果.

图3 零温、有限温度、强磁场下奇异夸克物质的组分随重子数密度和磁场的变化Fig.3.The fractions of SQM as functions of baryon density and magnetic fields with g-2 in zero temperature,finite temperature,and strong magnetic field cases.
图4 给出了不同温度下奇异夸克物质的声速随重子数密度的变化,可以发现夸克物质的声速皆小于光速,符合因果律;其次,对于T=50 MeV的情况,相同重子数密度下的声速的平方会随着温度的增加而增加,这与图2 所示的压强随着温度增加而增加的结论自洽,预示着温度升高可能会支持更大质量的致密星体.
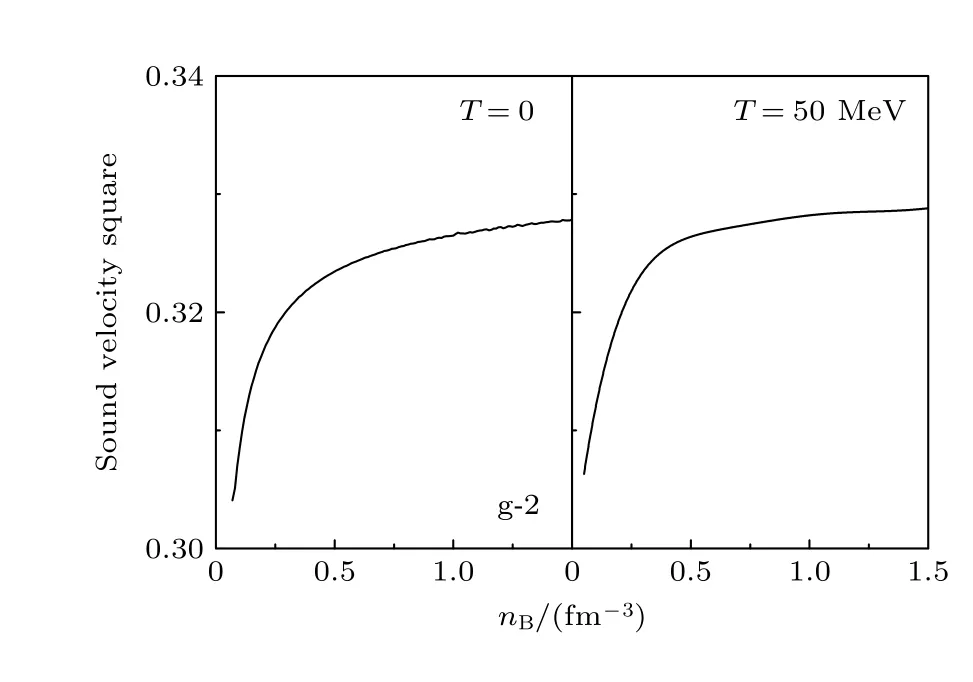
图4 不同温度下奇异夸克物质的声速随重子数密度的变化Fig.4.The sound velocity of SQM as functions of baryon density with g-2 at different temperatures.
4 夸克星计算结果
本文在星体的演化线上选取了三个等熵阶段来研究强磁场、有限温度情况下的夸克星,这类星体我们称之为原生磁星,具体的等熵阶段定义如下:

在之前的描述原生致密星体的工作[33,87–91]中,第一个等熵阶段出现在超新星刚刚爆发之后,人们将每核子熵设为1,中微子和电子的比例设为0.4(Yl=Ye+Yµ+Yνe+Yνµ=0.4);在第二个阶段,中微子在逃逸过程中会对原生星进行加热,此时的每核子熵增加到2;最后一个阶段,星体开始冷却并最终形成零温夸克星.
对于磁场下的原生星,如何定义磁星内部磁场的强度和方向分布是首要问题.对于磁星,从表面到中心的磁场强度会随着半径或者磁星物质重子数密度变化而变化,故人们一般通过引进密度相关磁场来描述磁星内部磁场强度的分布[49,50,53,54],可以写作:

这里Bsurf表示磁星表面的磁场,定义其大小为1×1015G,n0是正常核物质饱和密度,B0是决定磁星内部磁场强度大小的参数值,β0和γ可以通过调节磁星内部磁场强度的重子数密度依赖性来模拟磁星内部磁场强度分布,这里采用之前工作[92]中的较快减弱的磁场强度情况参数值(fast-B profile:γ=3,β0=0.001).从文献[92]中的图3可以看到,我们选取了 两种磁星内部磁场强度衰减的方案以及内部磁场随重子数密度的变化.由于磁星内部磁场强度具体分布未知,所以定义了“快速”与“慢速”下降方式.相比于“慢速”下降的参数取值,“快速”下降模式对磁星内部重子数的依赖程度更强.为了给出比较合理且平滑的磁场随重子数密度的下降曲线,经过调试,选择了γ=3,β0=0.001,使得星体表面磁场较弱(慢速下降会使得表面磁场较强)且重子数依赖平滑,对整个星体质量影响较小;调节参数B0时发现,如果选取B0=4×1018G,那么对于一般磁星的最大质量中心密度处的磁场可达到较为合理的B=1×1018G,同时在夸克星的表面处压强劈裂非常小.
由于磁星内部磁场强度与方向分布信息未知,故采用之前工作[92]的两种磁星内部磁场方向分布:第一种假设内部磁场沿着半径方向,我们称之为“径向磁场”;另一种内部磁场分布是磁场在垂直于半径方向的平面随机分布,我们定义为“横向磁场”.对于第一种情况,径向磁场会从一端传出并从另一端返回来保证无源;磁星表面磁场由于强度太低,表面的磁场效应以及外部磁场的磁效应可以近似忽略.由此定义,可以通过这两种非常极端的磁场方向分布情况来求解磁星的质量.
图5 描述了零温磁星内部磁星中心压强以及磁星的最大质量按照两种极端磁场方向分布情况随B0的变化,仍选取g-2 这套参数.发现随着B0的增加,中心压强和磁星的最大质量都出现了一定的“劈裂”,这说明磁星内部磁场方向对磁星物质的热力学性质以及磁星的最大质量都有影响.如果定义磁星内部压强的不对称度为由图5 可知,在B0较小的时候,压强与磁星随着磁场方向分布的劈裂很小,随着磁场强度的增加,横向压强增加、纵向压强降低.当B0=4×1018G时,可以发现中心密度处压强的不对称度达到17%(对于从磁星中心到表面处的压强不对称度皆小于此值).图5 中的上图绘制了磁星最大质量对应的半径随磁场的变化,可以发现横向磁场的最大质量半径随着磁场的增加而增大,反之,径向磁场情况随着磁场增加而降低.在图5的下图中,定义磁星最大质量不对称度为这里M⊥和M||分别代表了横向磁场情况与纵向磁场情况对应的磁星质量.可以发现,在磁场强度和温度为零的 时候,g-2 这套参数能够给出2.01 倍太阳质量夸克星,可描述PSR J0348+0432(质量为(2.01±0.04)M⊙[27]).在磁场增大的时候,横向磁场情况M⊥增加、纵向磁场情况M//减小.当B0=4×1018G时,发现磁星质量不对称度达到5%.由此可以得到结论:基于准粒子模型的磁星最大质量与磁星内部磁场强度和方向分布密切相关,会随着横向磁场的增加而增加,随着径向磁场的增加而减少.

图5 零温磁星中心压强以及磁星最大质量与对应半径按径向分布与横向分布随 B0的变化Fig.5.Pressure f or the central density,the maximum mass of magnetar,and the radius of longitudinal orientation case and transverse orientation case as functions of B0.
图6 给出了基于准粒子模型考虑径向磁场P||与横向磁场P⊥情况的原生夸克星演化中不同等熵阶段的原生磁星质量半径关系,仍沿用g-2 这套参数.在磁星强度分布里,在密度相关磁场中使用B0=4×1018G,可以看到,在图6的左图中,原生夸克星在T=0和B=0 情况下能够给出2.01 倍太阳质量夸克星,可描述PSR J0348+0432(质量为2.01±0.04M⊙[27]);考虑到有限温度的情况,当磁场为零时在等熵阶段I(II)S/nB=1,Yl=0.4(S/nB=2,Yl=0)中,发现夸克星的最大质量可以提升到 2.03M⊙(2.05M⊙),这意味着在准粒子模型的框架下,零磁场原生星的最大质量随着原生星的加热过程而增加.在考虑磁场之后,原生星在不同等熵阶段所对应的质量半径关系会随着径向、横向磁场分布的选择而劈裂.从图6 中图和右图可以看出,两幅图中的磁星的最大质量确实随着径向/横向磁场的选择发生了劈裂:对于S/nB=1,Yl=0.4 阶段,原生磁星的最大质量降低/增加到 1.99M⊙/2.06M⊙;对于S/nB=2,Yl=0 阶段,原生磁星的最大质量降低/增加到 2.02M⊙/ 2.08M⊙.这些结果表明不同等熵阶段原生磁星的最大质量会随着磁星内部磁场方向分布的径向/横向情况而减少/增加.计算结果表明,当选择密度相关磁场B0=4×1018G,γ=3,β0=0.001(fast-B profile)时,磁星的中心磁场在S/nB=1,Yl=0.4 阶段分别为7.8×1017G和 7.3×1017G;对于S/nB=2,Yl=0阶段,磁星的中心磁场分别是9.3×1017G和8.5×1017G,说明选取的这套参数实际上磁星内部磁场强度并不算大.

图6 原生星演化中不同阶段的原生磁星质量半径关系Fig.6.Mass-radius relations of the stages along the star evolution line of PQS with g-2 under the density-dependent magnetic field.
图7 给出了原生磁星在不同等熵阶段核心温度随磁星中心密度的变化,这里考虑零磁场情况和B0=4×1018G,γ=3,β0=0.001(fast-B profile)两种情况.从图7 可以看出,对于S/nB=1,Yl=0.4和S/nB=2,Yl=0 两个阶段,核心温度皆随着中心密度的增加而增加;当固定中心密度时,可以发现核心温度会随着磁场的增加而增加,S/nB=2,Yl=0 阶段的核心温度要高于S/nB=1,Yl=0.4的核心温度.计算结果表明,不考虑磁场时,原生磁星在S/nB=1,Yl=0.4 阶段的最大质量情况的核心温度为12.1 MeV,在S/nB=2,Yl=0 阶段为27 MeV.当考虑磁场后,磁星质量半径关系发生劈裂,S/nB=1,Yl=0.4 阶段在纵向/横向磁场情况的的最大质量情况的核心温度变为15 MeV/11.7 MeV;在S/nB=2,Yl=0 阶段,纵向/横向磁场情况的核心温度变为27.5 MeV/26.9 MeV,这说明原生磁星最大质量的核心温度不但与原生星演化中的加热过程有关,与磁星内部磁场强度和方向的分布也有关系.

图7 磁场与零磁场下原生星核心温度随中心密度的变化关系Fig.7.The core temperature for the star matter as a function of the central baryon density under zero magnetic field and B0=4×1018 G.
图8 考虑了磁星内部磁场方向分布的综合情况,即同时考虑纵向与横向磁场方向分布.这里将合磁场的方向与径向的偏移角度记为θ,在图8 中考虑g-2 参数、密度相关磁场参数为B0=4×1018G,计算了基于不同θ角的零温磁星质量半径关系.磁场为零时,g-2 参数所能给出的夸克星最大质量为2.01M⊙;当同时考虑横纵向 磁场且θ=10◦或θ=15◦时,磁星最大质量分别提升到2.11M⊙与2.17M⊙,反映出磁星最大质量与磁场方向和径向方向夹角的变化规律.在磁星内部,目前还不能确定其磁场强度与方向的分布,对于更一般的磁星内部磁场方向分布方案,在今后的工作中我们会持续深入讨论.

图8 纵向、横向磁场情况都考虑时,在g-2 参数、B0=4×1018 G 情况下基于不同 θ 角所计算的零温磁星质量半径关系Fig.8.Mass-radius relation for magnetars at zero temperature with g-2 and B0=4×1018 G at different θ.
5 总结
本文基于准粒子模型,研究了零温、有限温度、强磁场、有限温度强磁场下的 夸克物质的对称能、物态方程、组分等性质,发现温度场与磁场对奇异夸克物质的的每核子能量、每核子自由能、压强等热力学量影响非常大.
之后着重研究了在原生星演化中不同等熵阶段的原生磁星性质,采用 了密度相关磁场和两种极端磁场方向情况给出磁星内部磁场分布.结果表明原生磁星的星体质量、半径、核心温度、中心密度都会很大程度上受到温度场与磁场的影响.另外在中子星中,如果磁星内部磁场超过临界值(如Bcr=1×1018G),超子物质就有可能变得不稳定(原因可以来自磁场对星体物质压强的负贡献以及星体中心磁场的取值和磁场位形的参数化关系),这种不稳定性给中子星中心磁场设定了一个自然的上限[93],在今后工作中讨论核子夸克一阶相变对应的混合星物质时,可以考虑此限制.
因此本文的结论是夸克星内部的温度与磁场效应对于夸克星物质的热力学性质非常重要,原生磁星的最大质量不仅与星体演化中的加热过程有关,还与磁星内部磁场强度、方向分布密切相关.

