如何利用基本不等式求函数的最值
刘润军

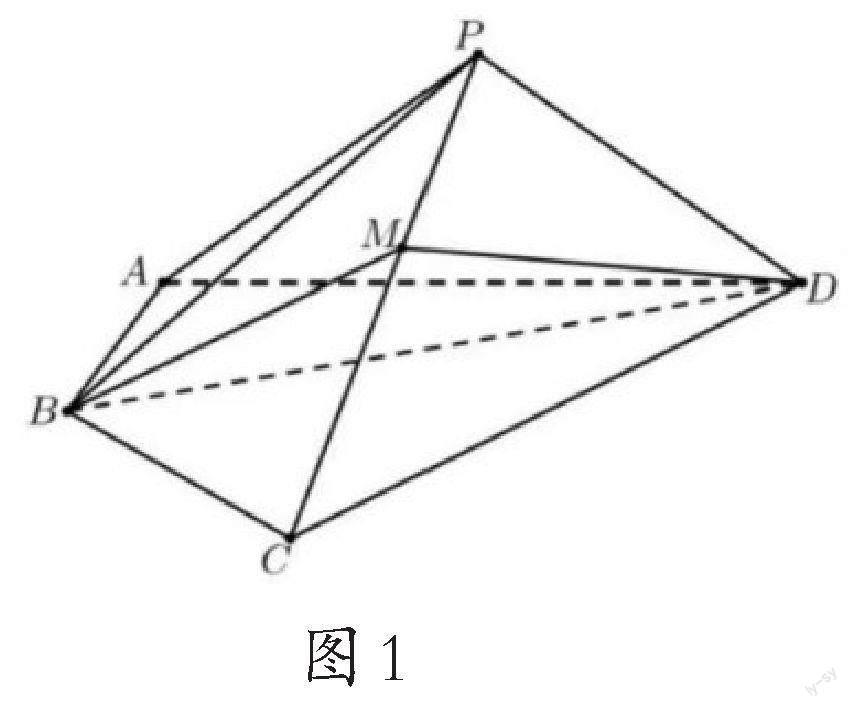

在运用基本不等式求最值时,往往要通过添项、去项、凑系数、凑分子、常数代换等方式来配凑出两式的和、积,并使其中之一为定值.
例1.已知0 解:因为8-2x>0,且2x+8-2x=8, 当且仅当2x=8-2x,即x=2时等号成立, 因此f(x)=x(8-2x)的最大值是8. 检验取等号是否成立是解题的必要步骤,若取等号时不等式不成立,就不能用基本不等式求最值,需寻找其他的方法,如利用对勾函数的单调性、导数法来解题. 解法2.由x+y=4可得y=4-x, 总之,运用基本不等式求函数的最值,需要注意:(1)将函数式进行合理的变形,以配凑出两式的和或积,并使其中之一为定值;(2)关注和式、积式的符号,确保各式都大于0;(3)在求得最值后,还需注意检验等号成立的条件是否满足题意. (作者单位:江苏省常州市金坛第四中学) 对一道二面角问题的解法的探究 范志君 二面角是指两个半平面所成的角,通常用二面角的平面角的大小来表示二面角.求解二面角问题主要有两种思路:(1)利用几何知识;(2)构建空间直角坐标系,利用空间向量知识求解.下面结合一道例题,探讨一下求解二面角问题的思路. 一、几何法 要求二面角的余弦值,需首先根据二面角的平面角的定义,过二面角的棱上的一点在两个半平面内分别作两条射线,则两个条射线所成的夹角即为二面角的平面角;然后根据平面角的位置,构造三角形,根据勾股定理、正余弦定理、三角函数的定义求得平面角的大小. 解:过P作PH垂直AD于点H,连接SH、AC, 因为平面MBD⊥平面ABCD, 所以M點的投影必在线段BD上, 也必在线段PC在底面的投影上. 又因为△PAD是等腰三角形, 且二面角P-AD-C是直二面角, 所以M点在底面的投影是△ACD的重心, 记为点O,连接OM, 作CH⊥DM.因为CN⊥DM, 所以DM⊥平面CNH, 所以NH⊥DM, 所以∠NHC是二面角B-MD-C的平面角. 解答本题,需从二面角的平面角的定义入手,证明CN⊥DM、NH⊥DM,即可根据平面角的定义确定二面角B-MD-C的平面角;然后添加合适的辅助线,构造△PCS、△MCD;再根据余弦定理、勾股定理求得平面角∠NHC的余弦值. 二、构建空间直角坐标系 对于规则的或容易找出垂直关系的几何图形,通常可根据几何图形的特点建立空间直角坐标系,通过 解法1.取AD的中点O,连接OP, 因为平面PAD⊥平面ABCD,AD为等腰直角三角形PAD的斜边, 所以OP⊥平面ABCD,分别以OD,OP所在的直线为y轴、z轴建立空间直角坐标系, 则P(0,0,1),A(0,-1,0),D(0,1,0), 因为AB2+AD2=BD2,所以AB⊥AD, 我们根据条件“二面角P-AD-C是直二面角,AD为等腰直角三角形PAD的斜边”,添加辅助线OP,即可构造出空间直角坐标系.再求得各个点、线段的坐标以及平面的法向量,即可通过空间向量的坐标运算求得问题的答案. 解法2.因为AB2+AD2=BD2,所以AB⊥AD. 连接AC,交BD于N,取AD中点H,连接PH,过点N作PH的平行线,分别以NC,ND所在的直线为x轴,y轴建立空间直角坐标系,如图2所示. 我们先根据AB⊥AD以及二面角P-AD-C是直二面角,来建立垂直关系;再添加辅助线,即可构造出三条互相垂直且交于一点的直线NC、ND、过点N且与PH平行的直线,并将其作为三条坐标轴,从而建立空间直角坐标系,求得两个半平面的法向量,即可根据平面向量的数量积公式求得二面角的余弦值. 相比较而言,几何法比较常用,只需根据相关的定义、定理、性质添加合适的辅助线,利用立体几何知识和平面几何知识求解.向量法虽然较为简单,但是解题过程中的运算量较大,同学们需谨慎计算.

