例谈动点的轨迹方程的四种求法

蒋程

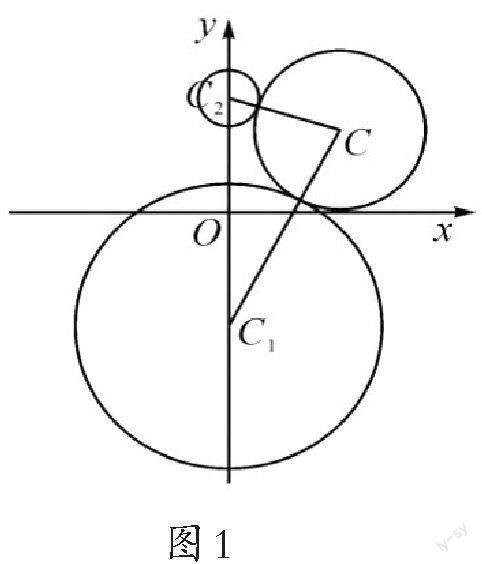
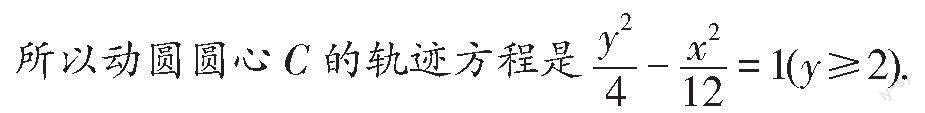
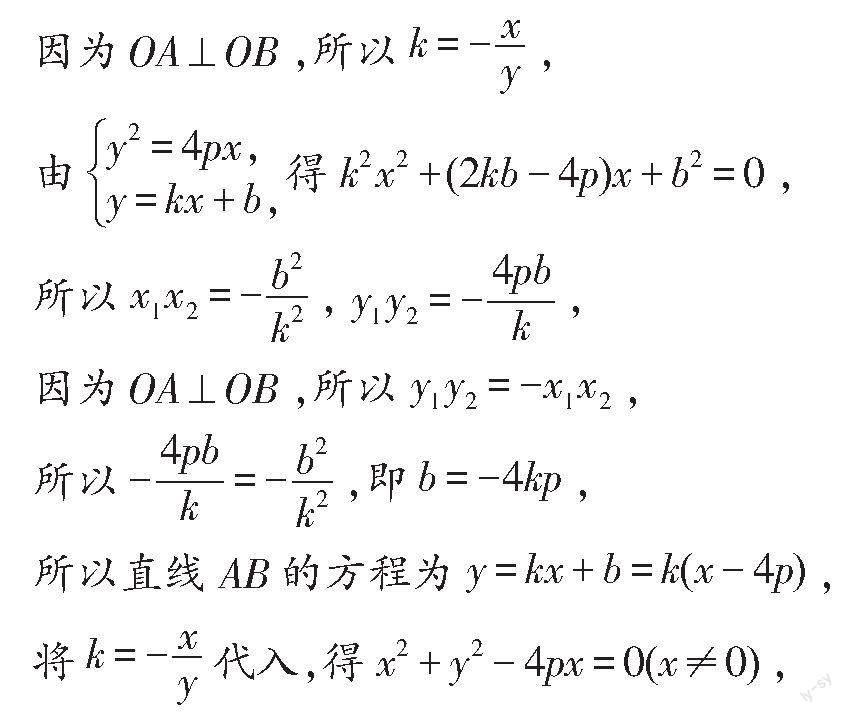
求动点的轨迹方程问题经常出现在解析几何试题中，这类问题侧重于考查同学们的推理、分析以及运算能力.求解这类问题的主要方法有定义法、参数法、相关点法和交轨法.下面结合实例，谈一谈这四种方法的特点以及应用技巧.

一、定义法

定义法是指运用圆锥曲线的定义解题.若发现动点的轨迹形如椭圆、圆、双曲线、抛物线或其中的一部分曲线，就可以根据椭圆、圆、双曲线、抛物线的定义，确定定点、焦点、焦点与动点之间的关系，求得椭圆、圆、双曲线、抛物线方程中的各个参数，便可以快速确定曲线的轨迹方程.

例1.如图1所示，已知圆C1：x2+（y+4）2=25和圆C2：x2+（y-4）2=1，某动圆C分别与圆C1和圆C2外切，求动圆圆心C的轨迹方程.

解：由题意知两圆的圆心为C1（0，-4），C2（0，4），半径为r1=5，r2=1，设动圆C的半径为r，

因为圆C分别与圆C1和圆C2外切，

所以|CC1|=r+5，|CC2|=r+1，

所以|CC1|-|CC2|=4<8，即点C到两定点C1、C2的距离之差为常数4，

所以动圆圆心C的轨迹是以C1、C2为焦点的双曲线的上支，

可得2a=4，2c=|C1C2|=8，所以b2=c2-a2=12.

结合图形分析动圆C与圆C1、圆C2的位置关系，即可发现|CC1|=r+5，|CC2|=r+1，即可得出|CC1|-|CC2|=4<8，由此可联想到双曲线的定义，即平面内到两定点的距离之差为定值的点的轨迹，确定动点的轨迹，求得a、b、c值，即可求得动点的轨迹方程.

二、参数法

参数法是解答数学问题的重要方法.若动点受某些变量的影响，而我们又无法确定这些变量的取值，则需运用参数法，即用参数表示出变量，设出直线的斜率、点的坐标、曲线的方程等，然后将其代入题设中，建立关系式，通过恒等变换消去参数，即可求得动点的轨迹方程.

例2.已知抛物线y2=4px（p>0）的顶点为O，A，B是抛物线上的两个动点，且OA⊥OB，OM⊥AB于点M，求点M的轨迹方程.

解：设M（x，y），直线AB的方程为y=kx+b，

即所求点M的轨迹方程为x2+y2-4px=0（x≠0）.

解答本题主要运用了参数法，即先引入参数x、y，

k、b、x1、x2、y1、y2，设出动点M的坐标、直线AB的方程以及A、B两点的坐标；然后将直线与抛物线的方程联立，根据一元二次方程的根与系数的关系建立关系式；最后通过恒等变换消去参数，得到关于x、y的方程，即为动点的轨迹方程.

三、相关点法

若两个动点之间存在某种特定的关系，则可以采用相关点法求解.先分别设出两个动点的坐标，并根据二者之间的关系，用所求动点的坐标表示另一个动点的坐标；然后根据另一个动点的几何关系，建立关于所求动点坐标的关系式，从而求得动点的轨迹方程.运用相关点法解题，要注意寻找两个动点之间的联系，并确定另一个动点所满足的几何关系.

例3.如图2所示，在圆x2+y2=4上任意选取一点P，过点P作x轴的垂线段PD，D为垂足，求线段PD中点M的轨迹方程.

解：设点M（x，y），P（x0，y0），

本题中P、M均为动点，且点M随着点P的运动而变化，需采用相关点法求解，先分别设出P、M两点的坐标；然后用M点的坐标表示P的坐标；再将其代入点P的轨迹方程，即可确定点M的轨迹及其方程.

四、交轨法

当问题中所求的动点为两条动曲线的交点时，往往需采用交轨法，即将两条动曲线的方程联立，消去

其中的参数，得到的关于x、y的方程即为所求的动点的軌迹方程.

仔细分析题意可知，M为直线A1P与直线A2Q的交点，且点A1、A2、P、Q都满足双曲线的方程，于是采用交轨法，求得两动直线A1P与A2Q的方程，再将两方程联立，消去参数，即可求出交点M的轨迹方程.

总之，求动点的轨迹方程，关键是要根据题目中的几何条件，寻找动点的横坐标与纵坐标之间的关系，建立关于动点的横坐标与纵坐标的方程.求动点的轨迹方程的方法很多，同学们需熟练掌握一些常用方法的特点、适用情形、解题思路，才能将其灵活地应用于解题中.