双向地震动的随机性对倾倒式危岩模糊可靠度的影响
张继旭,王林峰*,黄晓明,谭国金
(1.重庆交通大学 山区公路水运交通地质减灾重庆市高校市级重点实验室,重庆 400074;2.东南大学 交通学院,江苏 南京 211189;3.吉林大学 交通学院,吉林 长春 130012)
中国西部地区复杂的地形地质条件和频发的地震使得危岩崩塌成为中国西部地区常见的地震地质灾害类型[1-2]。2022年,四川泸定地震诱发的危岩崩塌灾害造成了人员伤亡和重大经济损失,且危岩崩塌灾害造成的人员伤亡占总伤亡的30%~40%,可见地震诱发危岩崩塌灾害的破坏力十分强大[3-4]。倾倒式危岩的稳定性主要由两条主控面控制,地震波的传播会进一步弱化主控面的强度,使得倾倒式危岩易失稳崩塌[5-6]。
以往研究多采用拟静力法计算倾倒式危岩的动力稳定性[7-8],但该方法无法反映地震动的时变特性,计算结果可能存在误差。在探究岩质边坡地震动力稳定性时发现,竖向地震动对结果的影响较明显[9]。Song等[10]认为水平地震激励下岩质边坡的峰值地面加速度约为垂直地震激励下的1.2~1.3倍。Korzec等[11]研究表明,如忽略竖向地震激励,边坡的永久位移低估率可达19%。因此,在倾倒式危岩地震动力稳定性研究中,不能忽略竖向地震带来的影响。进一步地,为考虑地震动的时变性,常采用基于结构动力学的方法研究边坡地震动力稳定性。陈训龙等[12-13]采用Newmark-β法求解了顺层岩质边坡在水平地震激励下的可靠度时程,采用Wilson-θ法求解了顺层岩质边坡在双向地震激励下的可靠度时程,并提出相应的可靠度评价方法。考虑地震动的随机性,对边坡进行随机地震动力分析更能反映其真实稳定性状态[14-15]。通过将地震激励视为随机过程,基于虚拟激励法[16]、振型叠加法[17]或概率密度演化法[18]求解岩质边坡在随机地震激励下的动力可靠度,优化边坡动力稳定性计算方法,可使计算结果更准确。
此外,危岩失稳事件属于模糊事件,采用经典可靠度理论判断危岩的稳定性状态可能存在误差[19]。Park等[20]基于模糊集理论建立了岩质边坡模糊可靠度计算方法。张永杰等[21]考虑了岩土参数隶属函数的分布特性对边坡可靠度的影响,为隶属函数的选取提供了参考。房光文等[22]提出考虑土体参数模糊随机性的土钉加固边坡可靠度计算方法。上述研究表明模糊可靠度能更准确反映边坡的稳定性状态。
综上,已有边坡随机地震动力稳定性的研究成果多数仅考虑单向地震动的随机性,且主要针对滑动破坏型岩质边坡,对于倾倒破坏的危岩体随机地震响应研究较少。因此,本文考虑双向地震激励的时变性和随机性,建立确定性地震激励和随机地震激励下倾倒式危岩模糊可靠度计算方法,探究双向地震动的随机性对危岩模糊可靠度的影响。研究成果为危岩随机地震动力稳定性评价和危岩工程治理提供参考。
1 倾倒式危岩地震响应计算模型
1.1 动力响应计算模型
倾倒式危岩稳定性主要由后缘主控结构面的抗拉强度及危岩体和基座间的抗拉强度决定,故将其简化为由主控结构面(cs1)和岩层分界面(cs2)控制的动力学模型。以倾倒式危岩重心在倾覆点内侧为例建立动力响应模型,两条主控面采用质量黏弹性模型[23]进行模拟。考虑水平和竖向地震动,建立倾倒式危岩动力学计算模型如图1所示[24]。
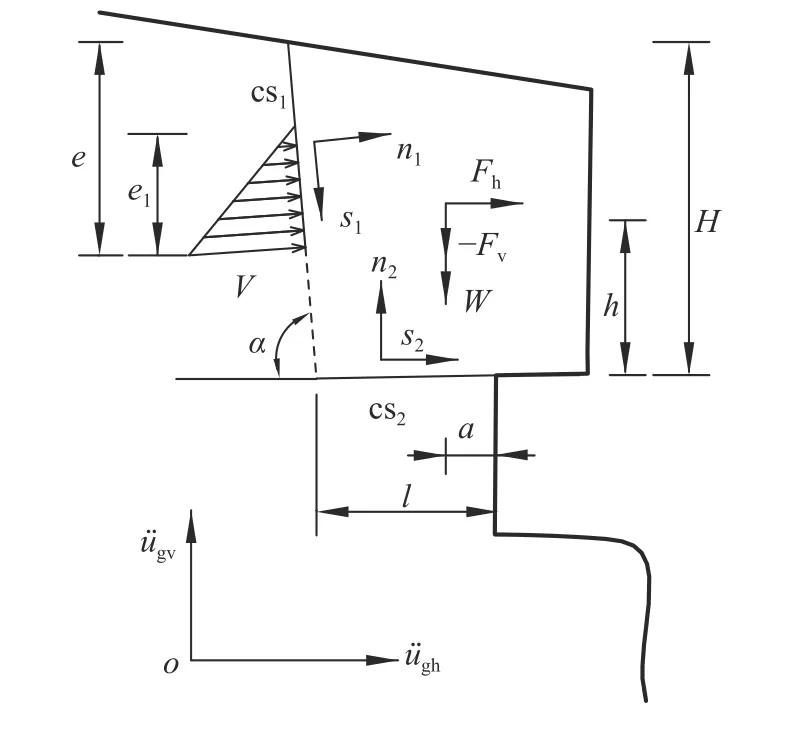
图1 倾倒式危岩动力学计算模型Fig.1 Dynamic calculation model of toppling perilous rock mass
图1中:W为危岩体重力,kN/m;V为裂隙水压力,kN/m;Fh、Fv分别为水平和竖向地震力,kN/m;H为危岩体高度,m;h和a分别为危岩体重心至倾覆点的高度和水平距离,m;e为主控结构面贯通段高度,m;e1为裂隙充水高度,m;l为危岩体底部主控结构面尖端至倾覆点的距离,m;α为主控结构面倾角,(°);u¨gh、u¨gv分别为输入的水平和竖向地震波加速度;n1、s1为主控结构面cs1的法向和切向;n2、s2为岩层分界面cs2的法向和切向。
1.2 动力运动方程
将危岩体视为刚体,采用集中质量法对倾倒式危岩动力学计算模型进行简化,等效为单自由度体系,两条主控面采用质量黏弹性模型模拟,建立倾倒式危岩质量黏弹性模型如图2所示。
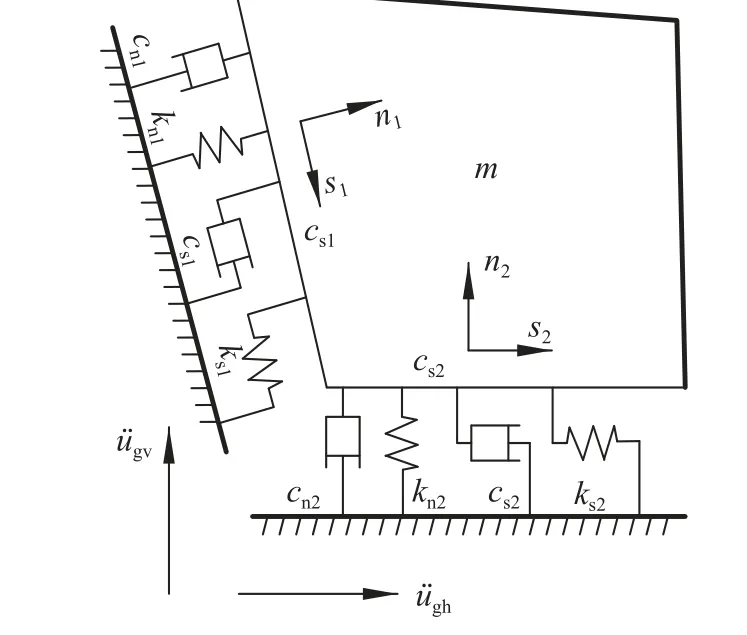
图2 倾倒式危岩质量黏弹性模型Fig.2 Mass visco-elastic model of toppling perilous rock mass
图2中,m为危岩体质量,cn1、cs1分别为主控面cs1法向和切向阻尼系数,kn1、ks1分别为主控面cs1法向和切向刚度,cn2、cs2分别为主控面cs2法向和切向阻尼系数,kn2、ks2分别为主控面cs2法向和切向刚度。
基于D’Alembert原理[25],建立危岩体在主控结构面cs1切向s1和法向n1上的运动方程如式(1)~(2)所示:
危岩体在岩层分界面cs2切向s2和法向n2上的运动方程如式(3)~(4)所示:
式(1)~(4)中,u¨s1、u¨n1分别为危岩体在s1和n1方向的地震加速度响应,u˙s1、u˙n1分别为危岩体在s1和n1方向的地震速度响应,us1、un1分别为危岩体在s1和n1方向的地震位移响应,u¨s2、u¨n2分别为危岩体在s2和n2方向的地震加速度响应,u˙s2、u˙n2分别为危岩体在s2和n2方向的地震速度响应,us2、un2分别为危岩体在s2和n2方向的地震位移响应。
2 危岩地震动力响应求解
2.1 确定性地震作用下危岩动力响应求解
本文采用Wilson-θ法[25]进行倾倒式危岩确定性地震动力响应求解。Wilson-θ法假设加速度在时间段[t,t+θΔt]内线性变化。首先,采用线性加速度法计算体系在ti+θΔt时刻的运动,其中θ≥1;然后,采用内插计算公式得到体系在ti+Δt时刻的运动。当θ≥1.37时,Wilson-θ法是无条件稳定的,本文取θ=1.4。
Wilson-θ法可求解t+Δt时刻的加速度u¨i+1、速度u˙i+1和位移ui+1,递推公式为:
式中:u¨i、u˙i、ui分别为体系在t时刻的加速度、速度和位移;u(ti+θΔt)为体系在t+θΔt时刻的位移,可通过插值计算。
由此,根据式(5)~(7)进行逐步计算,直接求解方程(1)~(4)即可得到危岩体在地震持时内的加速度、速度和位移响应结果。
2.2 随机地震作用下危岩动力响应求解
采用虚拟激励法[26]求解倾倒式危岩在随机地震激励下的动力响应。虚拟激励法的原理是将地震动加速度直接构造成含有地震动功率谱密度函数的虚拟激励。本文假定输入的地震动u¨g(t)为平稳高斯随机过程,其功率谱密度函数Sxx(ω)用Du-Chen功率谱密度模型[27],可表示为:
式中,D为震源辐射加速度脉冲宽度,ω为地震动频率,ω0为低频拐角频率,ωg、ςg分别为场地土的卓越频率和阻尼比,S0为基岩白噪声谱密度。
式中,i为虚数单位。
假设系统的响应为y(t),平稳随机过程x(t)的自功率谱为Sxx(ω),系统响应的自功率谱为Syy(ω,t)。在虚拟激励f(t)作用下,体系在t时刻的系统响应y˜(ω,t)可表示为:
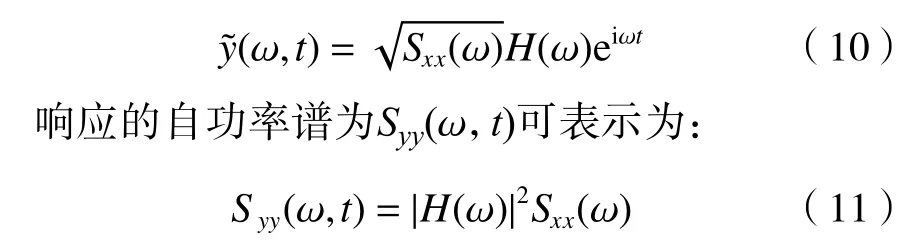
式中,H(ω)为频率响应函数。
将式(9)代入式(1)~(4)中,分别建立倾倒式危岩两条主控面cs1、cs2在随机地震激励下的虚拟运动方程:
式中,Sxxh(ω)、Sxxv(ω)分别为水平和竖向随机地震的功率谱密度函数,取竖向随机地震的S0为水平随机地震的0.65。
根据式(10)~(11)求解虚拟运动方程,即危岩在各方向上位移响应的功率谱密度为:

在求得任一随机地震响应y˜(ω,t)的功率谱密度后,对其进行积分可计算任一响应的时变方差,其表达式如下:
3 危岩随机动力模糊可靠度求解
3.1 危岩模糊可靠度
设Xn为影响危岩稳定性的随机变量,根据经典可靠度理论,其功能函数的表达式如下[28]:
从国企到民企,从济南到邹平,山东男篮东家的变更,不单纯是一次简单的体育市场交易:高速要坚持主业,西王要扩大影响力并为其进军运动营养产业提供足够分量的支撑点,市场成了一只看得见的手,促成了看得见的市场交易,除此之外,或许还有更多微妙的因素影响着这场“改朝换代”。

基于模糊失效准则对经典可靠度理论进行改进,以此来计算地震激励下倾倒式危岩的模糊可靠度。建立危岩失稳模糊事件的等效功能函数如下:
为计算危岩在地震激励下的模糊可靠度,将经典Monte-Carlo法计算事件失效概率中的示性函数变成隶属函数,并根据随机变量的概率分布形式进行模拟和抽样。Monte-Carlo法的抽样数目N=1×106。基于建立的等效功能函数得到发生失效的次数nf,从而计算失效概率和可靠度指标。倾倒式危岩模糊可靠度Ps可由式(26)计算:
3.2 确定性地震作用下危岩动力模糊可靠度求解
通过求解倾倒式危岩的运动方程,得到了危岩在主控面cs1和cs2的切向和法向位移,从而可根据式(27)~(30)计算其剪切力Fs1、Fs2和法向力Fn1、Fn2:
倾倒式危岩在水平和竖直方向的地震力合力计算公式分别为:
那么,倾倒式危岩动力稳定系数Fs(t)可根据式(33)计算,其中,Fv和Fh等于0的情况表示地震不存在,也即公式无意义,故不考虑。
式中:flk为危岩体抗拉强度标准值,kPa;fok为危岩体与基座间的抗拉强度标准值,kPa。
结合本文建立的倾倒式危岩动力响应计算模型,将两条主控面的抗拉强度参数flk和fok分别作为模糊随机变量X1、X2,根据式(23)~(24)可知随机变量X3的概率分布函数和密度函数分别为:
根据式(33)倾倒式危岩的动力稳定系数计算公式,可得到倾倒式危岩失稳模糊事件的等效功能函数:
式中,A1、A2、A3为系数,可根据式(33)计算。
3.3 随机地震作用下危岩动力模糊可靠度求解

式中,N0+为危岩地震响应平稳随机过程y(t)的穿零率;σy和 σy˙分别为地震响应平稳随机过程y(t)和其导数的标准差。
基于首次穿越破坏准则和随机过程理论[31],结合式(20)可以得到危岩地震响应峰值的均值和标准差分别为:

在得到剪切力和法向力的功率谱密度后,可根据式(20)求解主控面cs1、cs2上剪切力和法向力响应的时变方差;然后,根据式(31)~(32)分别计算水平和竖向地震力合力的时变方差;随后,将水平和竖向地震力合力的时变方差代入式(40)~(41)中可求解出地震力响应峰值的均值和方差;最后,可直接生成符合地震力响应峰值概率分布的随机数,并将其代入倾倒式危岩稳定系数计算公式中,便可按确定性地震作用下危岩动力模糊可靠度求解方法计算随机地震激励下危岩动力模糊可靠度。
4 算例分析
4.1 工程实例
研究区位于四川省乐山市罗一村,研究区发育的陡崖带位于大渡河东岸,陡崖带下方紧邻乐沙大道,来往车辆和行人较多。在不利条件下,该陡崖带一旦发生失稳崩塌,将严重威胁下方车辆和行人的安全并破坏顶部乡道设施,造成严重的人员伤亡和经济损失。罗一村陡崖带全貌如图3所示。

图3 罗一村陡崖带全貌图Fig.3 Overall view of the steep cliff zone in Luoyi village
通过现场踏勘,陡崖带发育3处危岩单体,总横宽约36.3 m,危岩单体高度约12.1~15.4 m,本文主要针对WY2危岩体进行分析。经现场测量,罗一村WY2危岩高约13.4 m,横宽约12.6 m,厚约12.1 m,危岩体体积约2 042.96 m3,主崩方向255 °,岩腔高度约6.4 m,岩腔深度约5.7 m。组成危岩体的地层为三叠系中统雷口坡组(T2l)灰岩和泥灰岩,危岩基座及岩腔主要出露泥灰岩和薄层泥岩,危岩顶部覆盖层主要为第四系全新统冲积层()砂质黏土,厚约1.5 m。危岩带现场照片和WY2危岩体地质剖面图分别如图4和5所示。参考文献[32-33]的岩体参数取值,结合罗一村危岩带的地质条件,将WY2危岩体及结构面的物理力学参数列入表1中。

表1 WY2危岩体及结构面的物理力学参数Tab.1 Physical and mechanical parameters of WY2 perilous rock mass and structural plane

图4 危岩带现场照片Fig.4 Photo of perilous rock mass zone
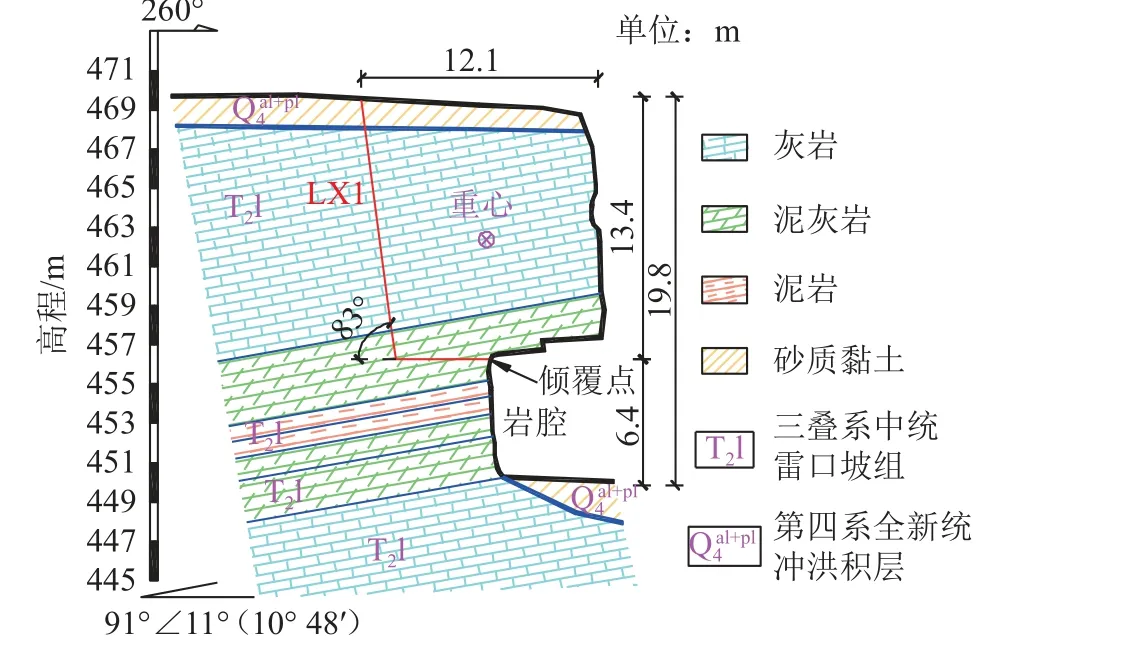
图5 WY2危岩体地质剖面图Fig.5 Geological section of WY2 perilous rock mass
4.2 危岩确定性地震动力模糊可靠度分析
输入的确定性地震波为汶川卧龙地震台NS向、UD向地震波,地震持时为150 s,取样周期Δt=0.1 s。工程场地地震基本烈度为Ⅶ度,危岩体阻尼比ξ=0.05,将地震波加速度幅值调至0.1g,卧龙地震波加速度时程曲线如图6所示。
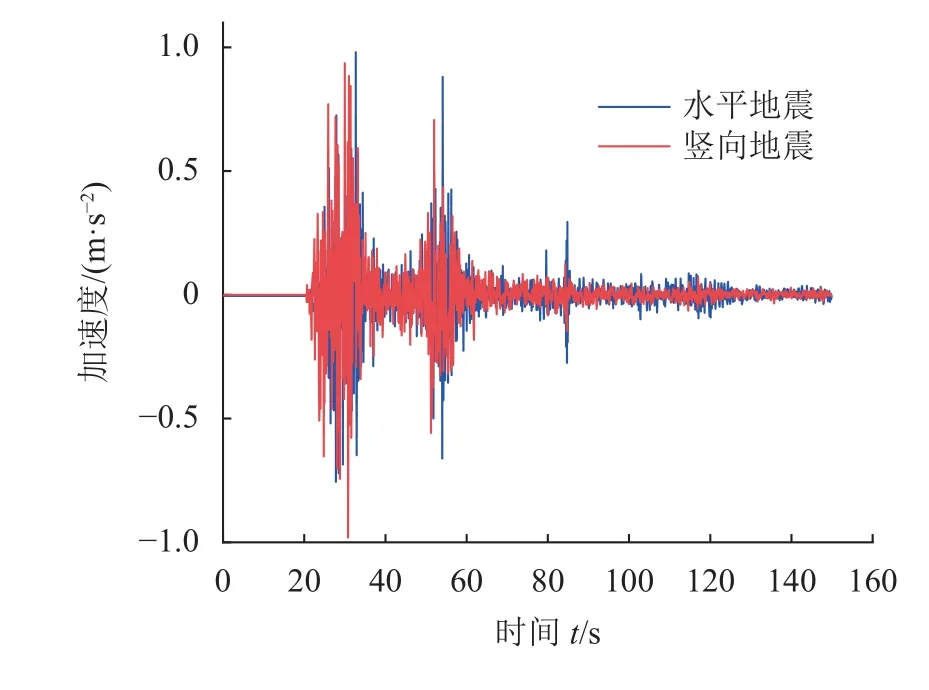
图6 卧龙地震波加速度时程曲线Fig.6 Acceleration time-history curve of Wolong seismic wave
基于第2.1节建立的倾倒式危岩确定性地震作用下动力响应计算方法,采用Wilson-θ法求解罗一村WY2危岩在双向确定性地震作用下的位移响应,结果如图7所示。
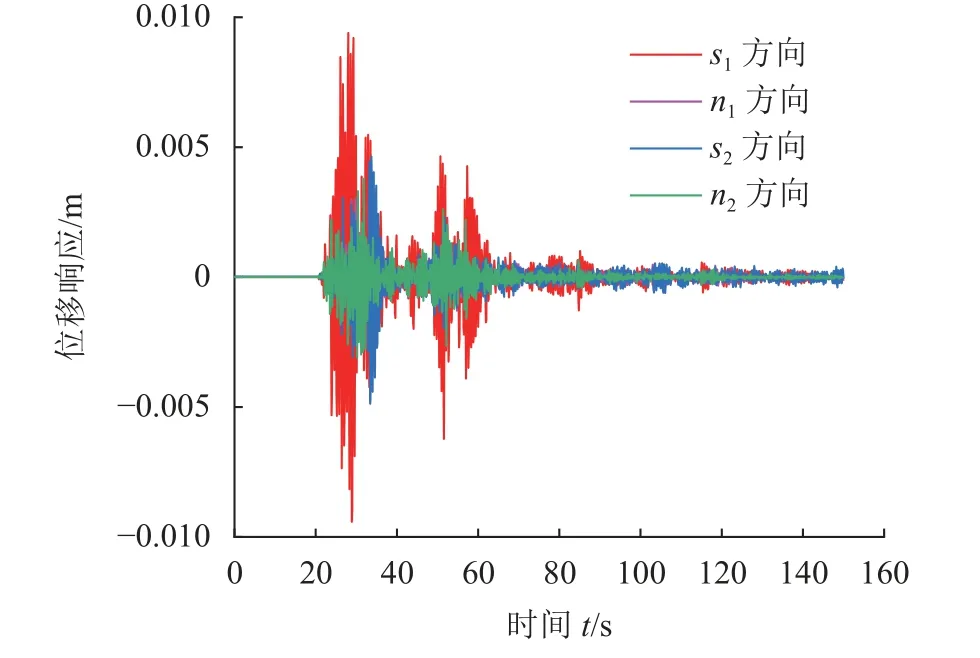
图7 罗一村WY2危岩体地震位移响应Fig.7 Seismic displacement response of WY2 perilous rock mass in Luoyi village
由图7可知:s1方向最大位移值为9.42 mm,出现在t=28.9 s时;n1方向最大位移值为4.79 mm,出现在t=33.4 s时;s2方向最大位移值为4.88 mm,出现在t=33.4 s时;n2方向最大位移值为3.80 mm,出现在t=31.9 s时。根据危岩体的位移响应结果,结合式(27)~(33)可计算得到危岩体在双向地震作用下的动力稳定系数时程曲线,结果如图8所示。
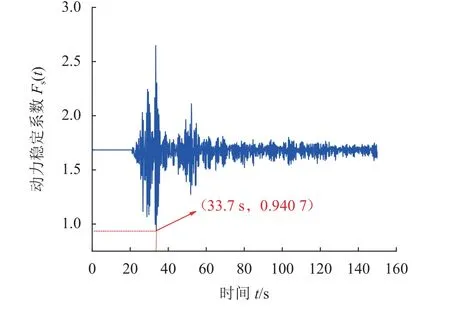
图8 WY2危岩体动力稳定系数时程曲线Fig.8 Time history curve of dynamic stability coefficient for WY2 perilous rock mass
由图8可知:当t=33.7 s时,危岩体的动力稳定系数达到最小值0.940 7;参考文献[34]的最小平均安全系数评价方法,可得危岩动力稳定系数Fs=1.202 6。
基于第3.2节建立的确定性地震作用下危岩动力模糊可靠度计算方法,将危岩抗拉强度参数flk、fok作为随机变量X1、X2,且均服从正态分布,其统计特征值见表2[32-33]。引入新随机变量X3,其统计特征可根据式(34)~(35)计算;采用MATLAB分别随机生成符合3个随机变量分布形式的106个数据计算WY2危岩体的动力模糊可靠度时程曲线,结果如图9所示。同时,基于传统的经典可靠度理论,计算得到WY2危岩体的动力经典可靠度时程曲线,结果如图10所示。

表2 WY2危岩体抗拉强度参数统计特征值Tab.2 Statistical characteristic values of tensile strength parameters for WY2 perilous rock mass
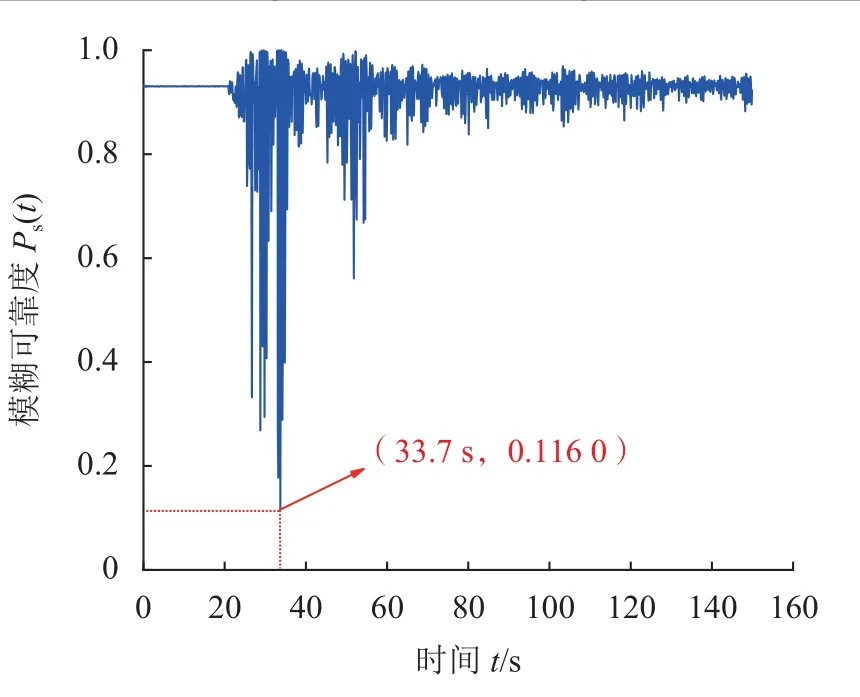
图9 WY2危岩体动力模糊可靠度时程曲线Fig.9 Time history curve of dynamic fuzzy reliability for WY2 perilous rock mass

图10 WY2危岩体动力经典可靠度时程曲线Fig.10 Time history curve of dynamic classical reliability for WY2 perilous rock mass
由图9可知:不考虑地震荷载,即t=0时,危岩体的模糊可靠度为0.931 9;当t=33.7 s时,危岩体的动力模糊可靠度达到最小值0.116 0,与动力稳定系数最小值出现的时刻一致,这表明建立的危岩动力模糊可靠度计算方法是合理的。由图10可知,该危岩体在t=33.7 s时,动力经典可靠度达到最小值0.205 2。
为评价危岩体的动力模糊可靠度,参考提出的最小平均安全系数评价方法[34],建立最小平均模糊可靠度评价方法,即最小平均模糊可靠度由式(46)计算:
式中,Ps0为静力作用下计算得到的危岩模糊可靠度,Ps(t)min为危岩可靠度时程曲线中的最小值。
因此,罗一村WY2危岩体的最小平均模糊可靠度Psmin=0.401 6;同理,可计算其最小平均经典可靠度为0.459 5。
4.3 危岩随机地震动力模糊可靠度分析
研究区的工程场地为Ⅱ类场地,取平稳随机地震持续时间T=40 s。根据场地条件可确定Du-Chen谱密度地震动模型的相关参数为[27]:D=0.011,ωg=17.72 rad/s,ξg=0.92,ω0=1.83 rad/s,S0=12.47×10-4m2·s-3。由上述参数可分别得到输入的双向平稳随机地震激励的功率谱密度(PSD)如图11所示。
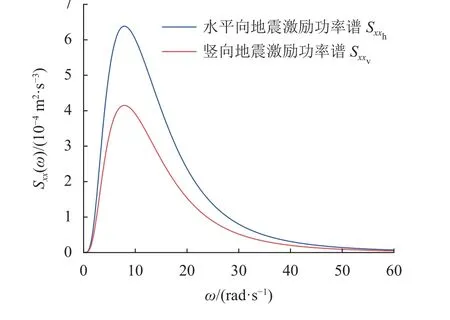
图11 输入的双向平稳随机地震激励的PSDFig.11 PSD with bidirectional stationary random seismic excitation input
基于第2.2节建立的倾倒式危岩随机地震作用下动力响应计算方法,采用虚拟激励法求解虚拟运动方程,得到了WY2危岩体在双向随机地震激励下位移响应的时变方差,结果如图12所示。图12表明:在双向随机地震激励下,WY2危岩体在s2方向位移响应的时变方差最大,即危岩体在s2方向上位移响应的离散程度最大,表明危岩体有可能产生s2方向的突变位移;s1方向和n1方向位移响应的时变方差大致相同,且与s2方向位移响应的时变方差较接近,表明危岩体可能沿着s1和n1合位移方向产生突变位移;n2方向位移响应的时变方差最小,即危岩体在n2方向上的位移变化较连续,危岩在n2方向产生突变位移的可能性较小。这一规律表明危岩体在双向随机地震激励下产生倾倒破坏的可能性较大,危岩体沿着主控面cs1产生滑移破坏的可能性较小,且不会出现沿n2方向发生破坏,与危岩实际破坏方式较为接近,符合现场的定性判断结果,验证了本文建立的理论模型和计算方法的合理性。
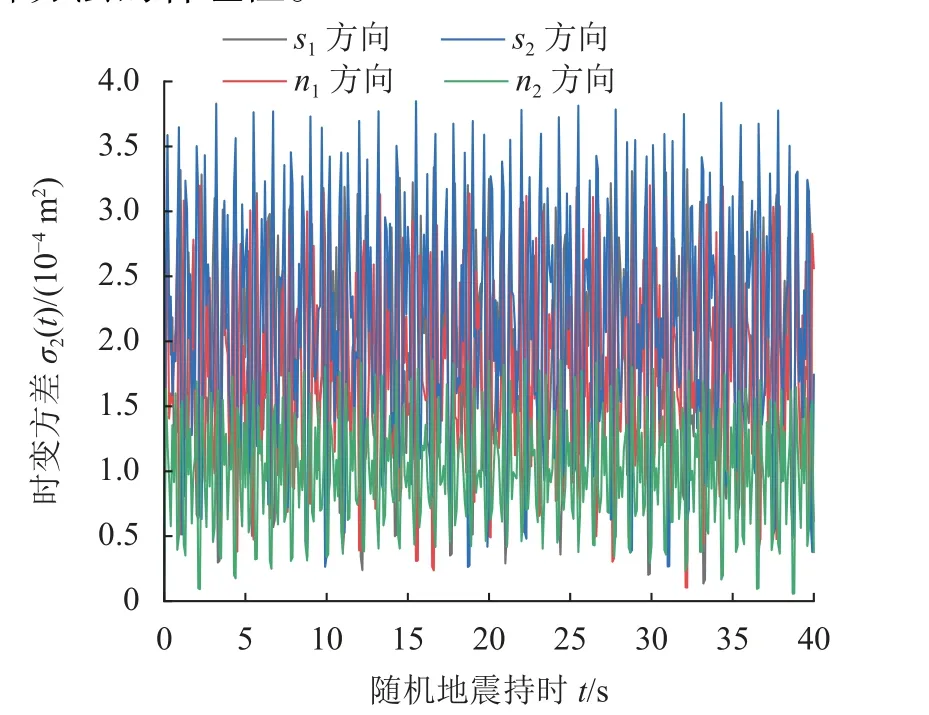
图12 WY2危岩体位移响应的时变方差Fig.12 Time varying variance of displacement response for WY2 perilous rock mass
基于第3.3节建立的随机地震激励下危岩动力模糊可靠度计算方法,首先,求解了WY2危岩体在双向随机地震激励下的随机动力稳定系数时程曲线,结果如图13所示。由图13可知:当t=21.4 s时,危岩体的动力稳定系数达到最小值1.058 1,故可得到危岩体在双向随机地震激励下的随机动力稳定系数Fs=1.278 9。
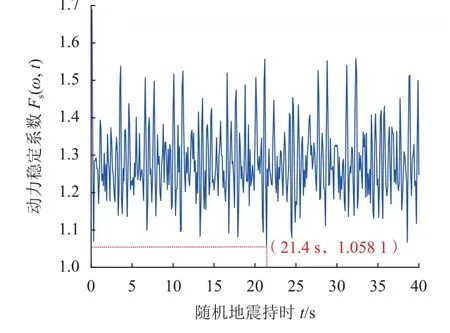
图13 WY2危岩体随机动力稳定系数时程曲线Fig.13 Time history curve of random dynamic stability coefficient for WY2 perilous rock mass
进一步地,求解得到WY2危岩体在双向随机地震激励下的随机动力模糊可靠度和经典可靠度时程曲线,结果如图14~15所示。由图14、15可知:当t=21.4 s时,危岩体动力模糊可靠度达到最小值0.257 1,动力经典可靠度达到最小值0.389 7,与随机动力稳定系数最小值出现的时刻一致,这表明建立的危岩随机地震动力模糊可靠度计算方法是合理的。
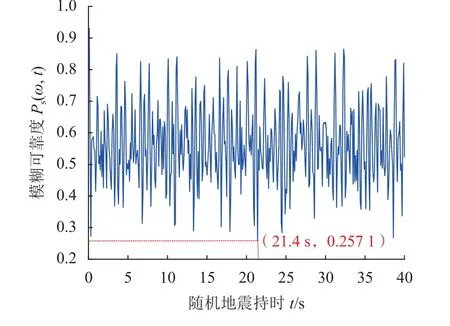
图14 WY2危岩体随机动力模糊可靠度时程曲线Fig.14 Time history curve of random dynamic fuzzy reliability for WY2 perilous rock mass

图15 WY2危岩体随机动力经典可靠度时程曲线Fig.15 Time history curve of random dynamic classical reliability for WY2 perilous rock mass
同理,为评价危岩体在双向随机地震激励下的动力模糊可靠度,采用最小平均模糊可靠度Psmin进行评价。基于式(46)得到WY2危岩体的最小平均模糊可靠度Psmin=0.493 3,最小平均经典可靠度为0.579 5。
4.4 对比分析
为探究双向地震激励随机性对倾倒式危岩动力模糊可靠度的影响,需对比确定性地震波和随机地震激励两种地震荷载形式对倾倒式危岩动力模糊可靠度的影响,将两种不同地震荷载形式作用下倾倒式危岩的动力模糊可靠度结果列入表3中。
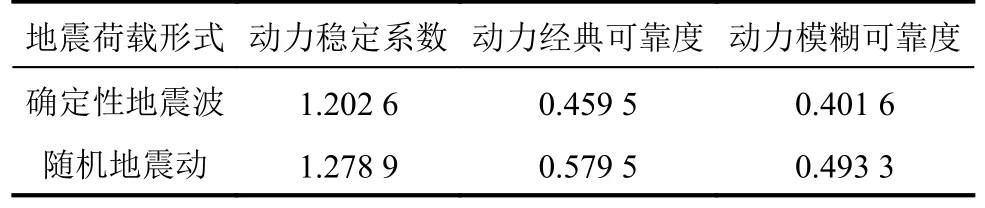
表3 WY2危岩体不同地震荷载形式下的动力模糊可靠度Tab.3 Dynamic fuzzy reliability of WY2 perilous rock mass under different seismic load forms
由表3可知,相比于确定性地震荷载,随机地震激励下WY2倾倒式危岩体的动力稳定系数增加了6.34%,动力经典可靠度增加了26.12%,动力模糊可靠度增加了22.83%。 这表明,考虑地震动的随机性后危岩体的稳定系数和可靠度会增大,符合文献[35]得出的地震随机性降低了岩质边坡失效概率的结果。这是因为工程中常常为了简化计算不考虑地震动的随机性,通常是按最不利工况进行取值,得出的危岩动力稳定性结果偏安全。考虑危岩体的模糊失效准则后,确定性地震波作用下危岩体的模糊可靠度相比于经典可靠度降低了14.42%,随机地震激励下危岩体的模糊可靠度相比于经典可靠度降低了17.47%,表明考虑模糊失效准则后的计算结果更偏于工程安全。模糊失效准则可以计算危岩在可靠和失效状态之间存在过渡区时的模糊可靠度,有助于更准确地判断危岩体真实的稳定性状态。
5 结 论
考虑地震动的双向性和随机性,对地震作用下倾倒式危岩动力响应及模糊可靠度进行了研究。分别采用Wilson-θ法和虚拟激励法建立了倾倒式危岩在确定性地震波和随机地震激励下的动力响应计算方法。根据危岩体的动力响应结果,基于模糊失效准则,采用Monte-Carlo抽样建立了动力模糊可靠度快速计算方法,并将理论方法应用到工程案例中,主要形成以下结论:
1)倾倒式危岩在双向确定性地震波作用下的位移响应较小,其动力稳定系数为1.202 6,进一步求解其模糊可靠度和经典可靠度分别为0.401 6和0.459 5。
2)将双向地震动视为平稳随机过程,随机地震激励下倾倒式危岩位移响应的时变方差结果为:s2方向>s1方向≈n1方向>n2方向,即危岩体在随机地震激励下可能的突变位移方向为s2方向及s1和n1合位移方向,验证了危岩体发生倾倒破坏的失稳模式。
3)考虑地震动的随机性后,危岩体的动力稳定系数、模糊可靠度和经典可靠度分别增加了6.34%、22.83%和26.12%。
4)引入危岩体的模糊失效准则后,确定性地震波作用下危岩体的可靠度降低了14.42%,随机地震激励下危岩体的可靠度降低了17.47%,即采用模糊失效准则计算得到的模糊可靠度更偏于工程安全。

