梁-H型柱弱轴刚性拼接的子结构抗倒塌性能试验研究

宋晓燕，钟炜辉,2*，孙 伟，陈 昊，王洪臣，韩曙华

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2.西安建筑科技大学 结构工程与抗震教育部重点实验室，陕西 西安 710055；3.中国建筑西北设计研究院有限公司，陕西 西安 710018)

由意外荷载作用引起的连锁反应可能会导致整个建筑物的倒塌[1]，能够预判和明确结构薄弱位置的变形性能和抗力演化机理，是有针对性地进行结构抗连续倒塌分析的关键。

梁柱连接节点是整个结构体系中的重要受力构件[2]，通常根据其弯矩和转角关系划分为刚性、半刚性、柔性节点[3-4]。其中，因刚性节点传力路径明确、建模方法简单的优点，使其在分析和实际应用时更为广泛。目前，针对刚性连接节点抗倒塌性能的研究不胜枚举，乔惠云[5]、Xuan Wei[6]、玄伟[7]等以梁柱刚性连接为前提，推导了不同竖向荷载作用下约束钢梁及空间钢框架各阶段的抗力发展情况并给出了显式表达式；李金威等[8]借助Ansys模拟了栓焊和狗骨连接的子结构在中柱失效条件下的破坏模式，对比了两种节点形式的子结构力学性能；Wang等[9]利用Ansys/LS-DYNA的显式计算程序对霍静思等[10]的3个刚性子结构试件进行了动力模拟，探究了荷载的动力效应对子结构抗倒塌性能的影响；Wang[11]、孙昕[12]、Zhong[13-14]、钟炜辉[15]等选取不同的子结构作为研究对象，通过一系列试验探索了刚性节点形式、梁线刚度对子结构抗力发展的影响，并在此基础上提出了改进结构抗倒塌性能的策略。然而，这些研究多围绕梁与H型柱强轴或钢管柱连接展开，对于H型柱弱轴方向设置过渡段后再与梁段刚性连接的子结构，其倒塌性能的研究少之又少，更不必说对比具体的节点形式对结构抗倒塌性能造成的影响，这将对获得结构准确的空间传力路径造成极大困难。

H型柱弱轴方向与梁进行刚性连接时常采用栓焊连接和全螺栓连接形式。采用栓焊节点进行连接时，钢梁翼缘与过渡段焊接易导致节点区出现焊接损伤缺陷[16-18]，致使结构提前发生破坏，而全螺栓连接的节点转动能力强，可有效促进结构位移的发展，延迟结构发生倒塌的时间。

备用荷载路径法是国际普遍认可的结构抗连续倒塌分析方法[19]，本研究基于该法并考虑楼板的组合效应，在前期的研究[20]基础上以带楼板的两跨三柱型组合梁柱子结构为研究对象，设计制作了钢梁与H型柱弱轴方向栓焊连接/全螺栓连接的子结构试件。对比分析了两种节点形式下子结构破坏模式、变形能力、抗力演化路径的差异。基于能量平衡原理获得了组合梁柱子结构在突加外载作用下的结构动力响应，客观评价了弱轴方向两种刚性拼接子结构的抗倒塌性能。

1 试验概况

1.1 试验子结构的选取

按照中国钢结构设计标准[21]设计了一个7层钢框架结构，结构层高3 300 mm，平面跨度4 500 mm×4 500 mm。设计恒荷载、活荷载分别为5.0、2.5 kN/m2。基于备用荷载路径法并考虑楼板的组合效应，从模型中提取组合梁-柱子结构。在中柱失效工况下，上部结构的竖向荷载集中作用于失效柱顶部，因此，假设失效柱上部受到竖向集中荷载P作用；中间层框架柱的反弯点位于其中部，框架梁外围约束构件的反弯点位于梁长的1/4处，对应于长度Ls，框架柱同时承受上部结构传来的恒定荷载P0。由此得到两跨三柱型组合梁柱子结构模型，如图1所示。图1中，L为梁跨度，LC为边柱高度。

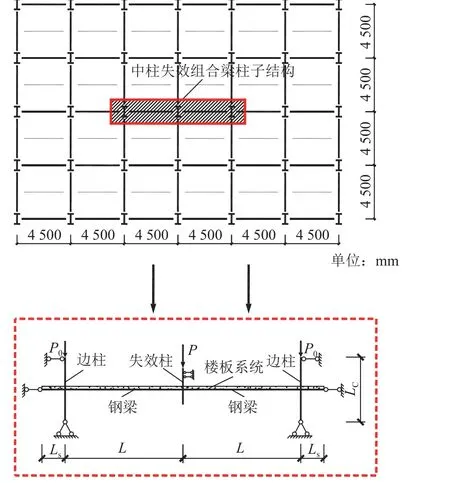
图1 两跨三柱型组合梁柱子结构模型Fig.1 Composite beam-column substructure with three columns and two beams

1.2 试件设计及材性

本缩尺试验的目的是通过拟静力加载试验揭示或阐述结构倒塌全过程的抗力演化和机制发展。根据现有的试验条件和目的，选用的试件缩尺比例为1∶3。试件几何尺寸及节点细部构造如图2所示。图2中，试件组合梁跨度L为1 500 mm，边柱高度LC为1 100 mm，所用钢材等级均为Q235B，钢梁、柱分别为热轧H型钢HM150 mm×100 mm×6 mm×9 mm、HW150 mm×150 mm×8 mm×10 mm。为避免梁柱直接连接时因截面尺寸不协调引起的应力集中问题，参考规范和文献[22-25]给出的设计方法进行H型柱弱轴方向的试件设计。首先设置悬臂梁段作为过渡段，过渡段一侧与柱全焊，另一侧与中间梁段连接，连接形式为栓焊的试件命名为RWUF，连接形式为全螺栓的试件命名为RWUT。两试件均设置长度为210 mm的悬臂梁段作为H型柱弱轴方向的过渡段，悬臂梁段翼板厚度为10 mm，腹板厚度为6 mm。对于试件RWUF，中间梁段与悬臂梁段翼缘焊接，腹板高强螺栓连接。根据等强设计原则，试件RWUT的盖板宽度与梁宽相等，厚度为10 mm；夹板高度为110 mm，厚度为8 mm。H型柱强轴方向伸出300 mm长的垂直梁段以考虑实际情况下另一个方向钢梁的布置及其对楼板的支承作用。试件螺栓均采用10.9级M16的高强螺栓，螺孔直径为18 mm，预紧力为100 kN，摩擦面抗滑移系数为0.35。楼板厚度根据缩尺比例且考虑钢筋、栓钉排布取为55 mm，保护层厚度10 mm，楼板宽度600 mm，板内配置了上下两层强度等级为HPB300的纵向受力钢筋，受力筋为Φ10@125，分布筋为Φ6@125，配筋率0.95%。组合楼板与钢梁通过直径为13 mm、长为45 mm的栓钉完全抗剪连接，压型钢板采用开口式YX 28-200-600，厚度为0.6 mm。

图2 试验试件几何尺寸及节点细部构造Fig.2 Geometric dimension of specimens and connections

通过电液伺服万能试验机及其配套采集系统获得的钢材材性见表1。在浇筑混凝土楼板时同条件预留材性试块，测得其立方体抗压强度平均值为17.9 MPa，轴心抗压强度平均值为13.1 MPa，弹性模量平均值为2.41×104MPa。

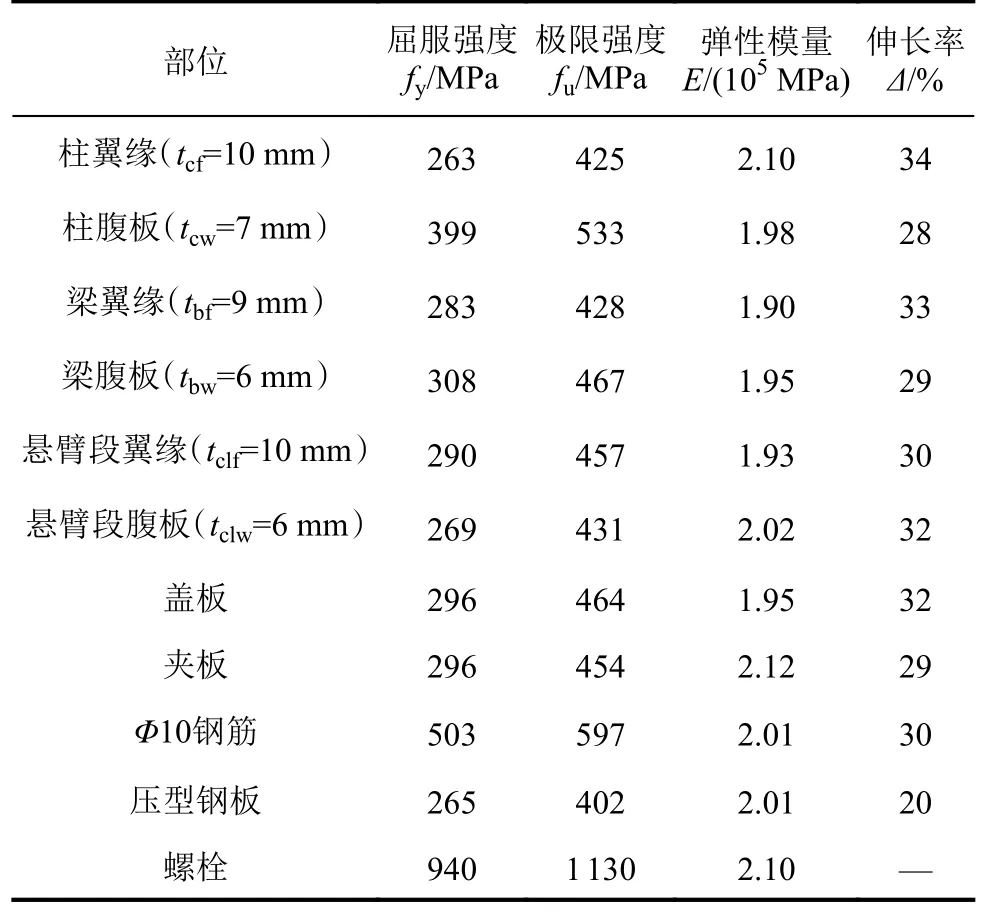
表1 钢材材性Tab.1 Material properties of specimens

1.3 加载装置

试验加载装置如图3所示。加载过程[14-15]如下：边柱顶部通过稳压千斤顶按0.3的轴压比施加竖向力以模拟上部结构的荷载作用；边柱上端设置为水平铰接连接，与横向横梁通过100 t的拉压传感器相连作为柱顶的水平铰接约束；边柱中部的组合梁端按照图1所示的反弯点位置简化为水平铰接连接与横向横梁通过100 t的拉压传感器相连作为组合梁端的水平铰接约束；边柱底部铰接于刚性地梁作为柱底竖向铰接约束；失效柱顶部通过长螺杆与100 t的液压伺服作动器相连，并利用后者施加拟静力荷载；失效柱底部连接可拆卸的竖向滑动装置，确保试件的竖向移动；失效柱平面外方向设置侧向约束装置，防止试件的平面外失稳。

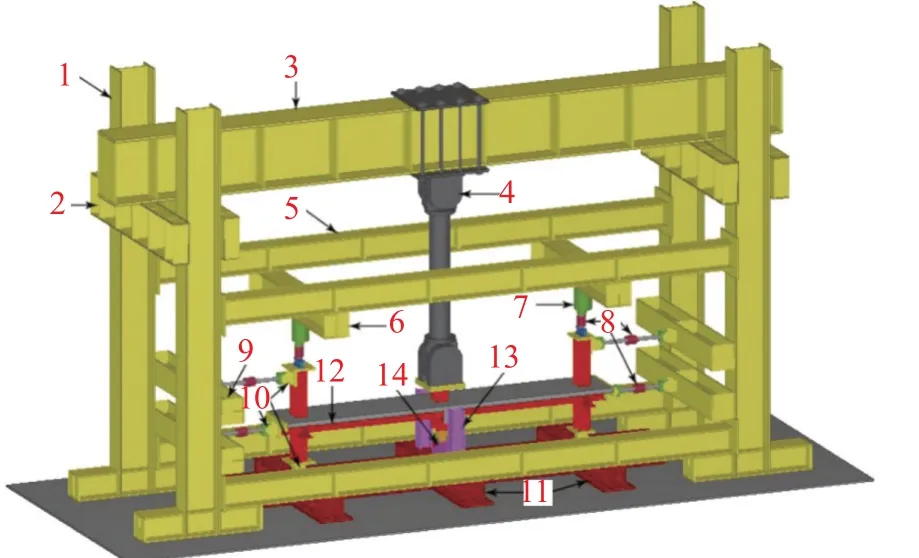
图3 试验加载装置Fig.3 Test setup

1.4 加载方案及破坏准则

备用荷载路径法不考虑柱的失效过程和原因，只考虑与失效柱相连的主要构件在荷载作用下的性态变化。柱失效后，上部荷载以集中力形式作用于柱顶。全过程控制加载速率不超过5 mm/min以保证整个加载过程是“静态”的，各级之间持荷3～5 min，确保结构发生稳定的变形后再进行下一级加载。当子结构试件丧失承载能力或梁端转角达到0.2 rad时[26]，试验终止。

1.5 测量方案

试验测量重点关注组合梁和边柱的变形、关键截面应变、节点转角等。靠近梁柱节点处、梁跨中截面为组合梁的关键截面，自左至右分别命名为B1～B6截面；边柱靠近柱底铰接连接处为柱的关键截面，自左至右分别命名为C1～C2截面。在关键截面处，各部件均布置应变片以便进行内力分析和计算；B1～B6截面处同时布置竖向位移计D2～D7监测组合梁的变形形态发展过程。位移计D1和D8布置在组合梁端部的水平方向上，结合边柱水平拉压传感器TC2、TC5和TC3、TC6可获得试件变形的任意时刻外界为组合梁提供的侧向刚度。边柱顶端布置了两个竖向拉压传感器TC1、TC4，实时监测额定竖向荷载作用。在梁柱节点附近同时布置了倾角仪I1～I6用于捕获子结构倒塌全过程节点转角的发展。试件RWUT关键截面B1、B3、B4、B6分别距近端柱中心线345 mm，截面B2、B5位于组合梁跨中；试件RWUF关键截面B1、B3、B4、B6分别距近端柱中心线300 mm，截面B2、B5位于组合梁跨中。以试件RWUT测点为例，具体的测点布置如图4所示。

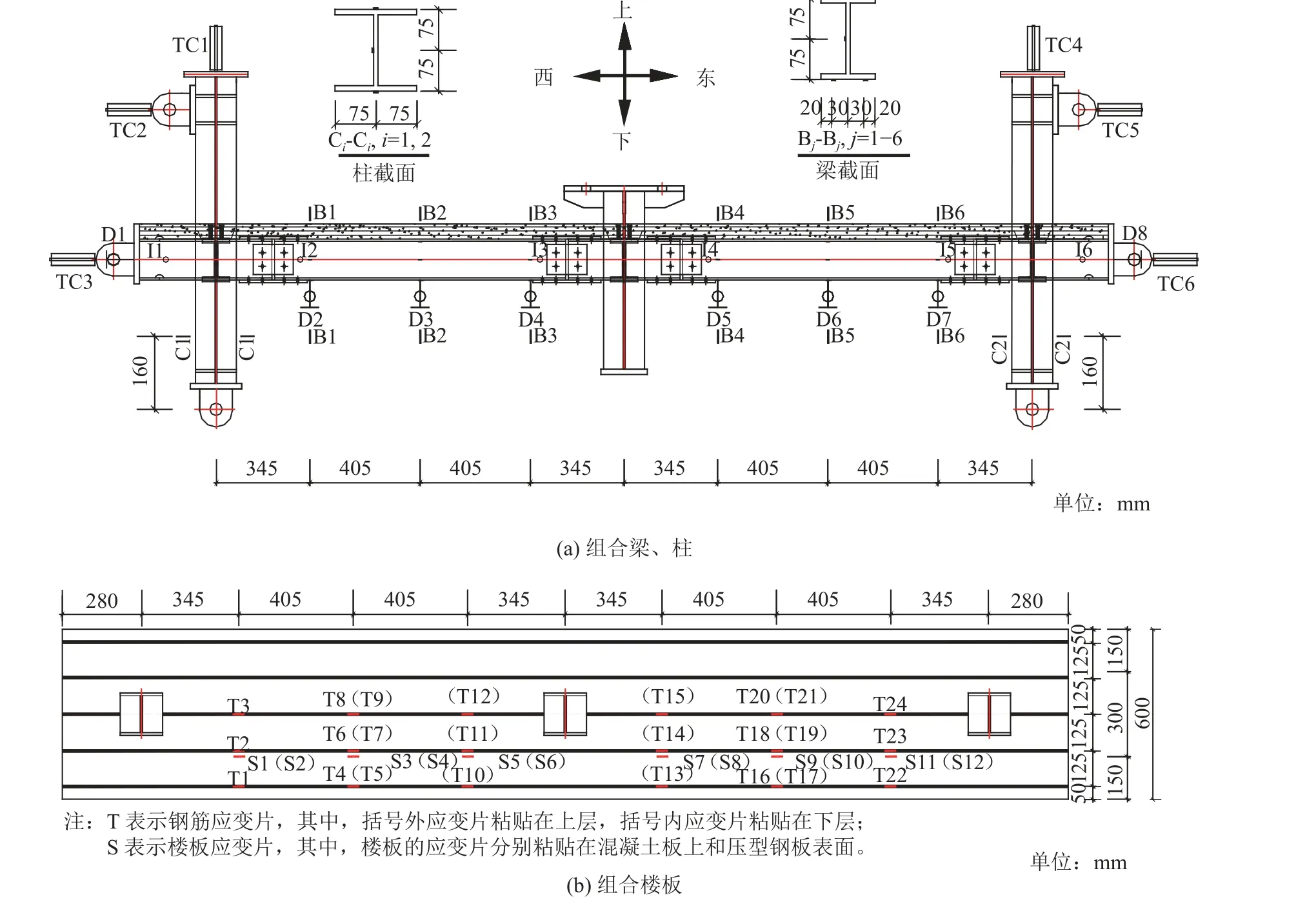
图4 试件RWUT测点布置Fig.4 Measuring point arrangement of RWUT

2 试验结果及分析

2.1 荷载-位移曲线及破坏现象

试件的荷载-位移曲线及试验关键点如图5所示，试件破坏模式如图6、7所示。试件受荷全过程均经历了弹性阶段、压拱阶段和混合机制阶段（梁机制与悬链线机制的混合阶段）。

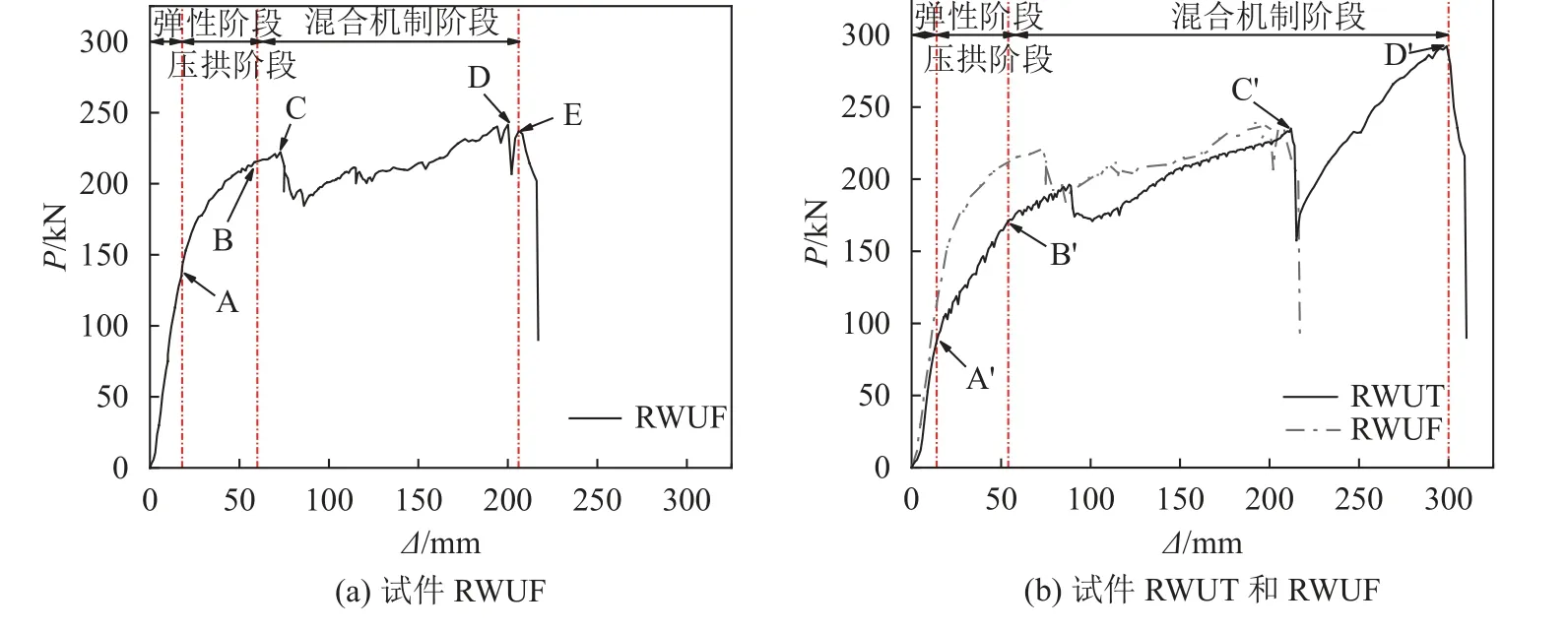
图5 试件荷载-位移曲线对比Fig.5 Comparison of load-displacement curves

图6 试件RWUF破坏模式Fig.6 Failure phenomena of specimen RWUF

2.1.1 试件RWUF

由图5（a）可见：试件RWUF弹性阶段OA（0≤ Δ≤18 mm）无明显的试验现象，试件荷载随位移增加线性发展；随位移的增加，组合梁内力呈现出显著的负向轴力，试件进入压拱阶段AB（18 mm＜ Δ≤60 mm），在此阶段，压型钢板剥离并鼓起（图6（a）），混凝土产生了沿板宽及梁长方向的裂缝；试件位移到23 mm时，抗弯承载力达到设计值PP（165 kN）；当轴力由负值转变为正值时，压拱阶段结束，此时试件抗力已达到216 kN。当试件进入混合机制阶段BE（60 mm＜ Δ≤206 mm），加载位移达到73 mm时，B4截面处钢梁受拉下翼缘焊缝发生断裂（图6（b）），荷载由222 kN掉落后再次攀升到C点；随位移的增加，B1/B6截面拼接节点处钢梁受压翼缘发生屈曲变形（图6（c）），楼板形成贯通长裂缝并被掀起（图6（d）），在此期间，钢材的开裂持续向腹板扩展，轴力得到有效传递，荷载-位移曲线逐步攀升；当位移发展至193 mm时，断裂侧受拉螺孔附近形成断裂轨迹，下、上螺栓孔于位移为200、206 mm时（D、E点）相继被拉裂（图6（e）），抗力由242、237 kN连续跌落，试件丧失承载力，加载结束。

2.1.2 试件RWUT

由图5（b）可见：试件RWUT弹性阶段OA′（0≤ Δ≤14 mm）无明显的试验现象，试件的荷载与位移呈线性关系；当试件进入压拱阶段A′B′（14 mm＜ Δ≤54 mm）时，组合梁轴力为负值，混凝土产生沿板宽及梁长方向的“八”字形裂缝，压型钢板剥离（图7（a））；拼接处螺栓滑移使得荷载-位移曲线出现剧烈抖动特征，部分荷载被消耗后又达到新的受力平衡状态，此阶段荷载随位移的增长趋势较弹性阶段缓慢，并于位移为50 mm时抗弯承载力达到设计值PP（165 kN），压拱阶段结束时试件抗力达到171 kN。试件进入混合机制阶段B′D′（54 mm＜ Δ≤300 mm），当位移达到88 mm时，试件发出崩响的同时，左跨柱间产生通长裂缝（图7（b）），节点拼接处拼接缝宽度增大，B1截面拼接处下盖板压曲变形（图7（c））；随着位移的持续增加，边柱附近压型钢板被撕裂（图7（d）），混凝土板被压溃/上下贯通，此阶段响声明显较前期少且轻，试件关键截面较为完整，塑性铰区截面弯矩因楼板退出工作稍有减小，但组合梁全截面轴力迅速发挥，试件整体抗力持续增长；当加载至C′点（214 mm）时，B4截面拼接处受拉侧盖板沿螺孔截面发生断裂（图7（e）），断裂截面螺孔被拉长至椭圆形，荷载从234 kN跌落至157 kN后又迅速回升直至加载结束。

图7 试件RWUT破坏模式Fig.7 Failure phenomena of specimen RWUT

两试件在各阶段破坏特征存在异同点：破坏均发生在正弯矩区塑性铰处，负弯矩区节点处受压部件发生屈曲变形；塑性铰出现在梁-梁拼接处，避免了梁柱节点核心区的破坏；得益于塑性铰的转动和轴力的发挥，试件整体抗力在加载后期均得到提高。采用相同的抗力设计方法得到的弱轴栓焊连接试件，首次断裂处于混合机制阶段前期，塑性铰处已达到极限弯矩，但组合梁的轴拉力正处于发展初期水平较低，断裂使得轴力丧失了进一步发展的路径，结构抗力转由腹板螺栓传递，荷载在大幅掉落后提升速度波动且缓慢；弱轴全螺栓连接试件首次断裂处于混合机制阶段中后期，节点的非线性转动保证了结构位移的发展，塑性铰达到其极限抗弯承载力，且组合梁截面的轴力已充分、显著发挥，断裂发生时，轴力已具备较高的发展水平，断后荷载的攀升更为迅速。此外，除钢材断裂、混凝土损伤的耗能途径外，螺栓发生有限滑移为节点的非线性转动提供了条件，对结构在受荷后期抗力的提升是有利的。

2.2 关键点性能需求分析

各关键点处的荷载-位移关系见表2。由表2可知：从抗力需求来看，两试件均在压拱阶段达到塑性设计的理论值，试件首次断裂荷载均在1.38PP左右，并能在断后发挥轴力保证结构抗力的持续增加。从变形特征来看，RWUF试件首次断裂发生在混合机制阶段初期，拼接处焊缝达到承载力极限后发生断裂；RWUT试件首先通过螺栓滑移耗散能量，滑移结束后，螺栓孔壁持续受到挤压发生轴向变形，塑性铰的快速转动和轴力的持续发挥，使得其悬链线效应显著发挥，试件首次断裂位移约为栓焊试件的3倍。

表2 关键点处荷载-位移对比Tab.2 Comparison of load-displacement curves at key points

采用变形能Q作为倒塌评价指标[27]可知，RWUF试件在位移发展初期能够发挥更迅速的抗力响应，但早期的断裂特征使其悬链线机制的抗力未得到充分发挥便丧失了可靠的传递路径，能量无法得到持续累积；而RWUT试件在前期的抗力响应小，反而为其大变形阶段更大的抗力响应积蓄了能量，其结构位移将超过倒塌限值且抗力仍具备传递路径。

2.3 组合梁变形曲线

试件在组合梁关键截面B1～B6的测点为D2～D7，失效柱处的测点D0，测点竖向位移随失效柱加载位移v的变化曲线及试件整体变形情况如图8所示。

图8 两试件整体变形发展过程对比Fig.8 Comparison of overall deformation

由图8可见：试件RWUT的变形曲线较RWUF更为饱满；在任意加载位移下，失效柱与两边柱的连线形成一条完整的曲线。小变形时，该曲线为二次曲线；位移增加时，该曲线逐渐被拉直为折线，这与试件内力由弯曲抗力向轴向抗力过渡一致。试件局部刚度的变化会影响子结构的进一步变形。当塑性铰处发生断裂后，破坏截面迅速扩张，使得断裂侧的结构刚度减小，断裂跨测点的位移变化将快于未断裂跨，对称跨度的试件子结构呈现不对称的变形曲线。

2.4 边柱变形曲线

两试件的边柱变形关系曲线如图9所示，图9中，关键点与图5所示试件加载全过程的关键点一致。由图9可见：加载初期，两试件边柱均存在较小的水平负向位移，后又回到0，这是由于压拱效应[28]引起的。位移由0向正值发展初期，边柱的受力情况一致，变形曲线基本重合；当试件发生断裂或滑移时，断裂（滑移）侧的组合梁内力被释放，由梁端约束作用引起的边柱水平变形发展停滞甚至回弹；随着位移的持续推进，梁内轴力发挥作用带动边柱中部发生迅速变形响应，直至加载结束。因节点优良的非线性转动能力，试件RWUT在加载后期发挥了显著的悬链线效应，其边柱水平变形大于试件RWUF。

图9 两试件边柱变形对比Fig.9 Comparison of side column deformation

3 内力发展及机制分析

3.1 内力及抗力机制

子结构的边界刚度可充分满足子结构内力发展需求，且全过程无能量损失，组合梁柱子结构倒塌全过程中的抗力P由梁机制抗力PM和悬链线机制抗力PN共同组成，即：

假定同侧梁段轴力沿梁长方向保持不变，不考虑混凝土的受拉作用，可知悬链线机制抗力PN由截面轴力的竖向分量组成，即：

式中，N为组合梁的轴力。

大位移情形下，组合梁的轮廓呈现出直线变形形态，假定同段梁的两端转角平均值为该段梁的转角。在加载过程的任一平衡状态下均采用图10所示的抗力计算模型计算试件内力。

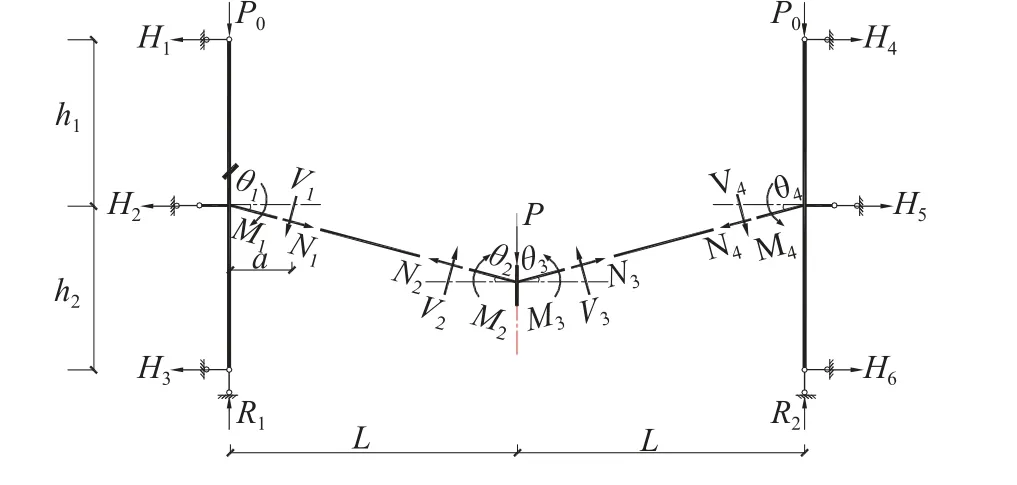
图10 中柱失效情形下组合梁柱子结构抗力计算模型Fig.10 Force equilibrium of composite substructure under a middle column loss

图10中，P0为两边柱的轴向恒定荷载。两边柱截面C1/C2处测得的应变小于钢材的屈服应变，因此，可采用弹性理论计算得到柱底反力H3、H6和R1、R2。结合柱侧拉压传感器的测量结果H1、H2、H4、H5可得到两跨梁的轴力为：

式（3）～（4）中：HL、HR分别为左、右跨梁的水平合力，HL=H1+H2+H3，HR=H4+H5+H6；VL、VR分别为左、右跨梁的竖向合力,VL=R1-P0，VR=R2-P0；θL、θR分别为两跨组合梁的梁端转角，θL=(θ1+θ2)/2，θR=(θ3+θ4)/2。

取柱与梁端形成的隔离体计算力学平衡，由水平、竖直方向力的平衡可得到梁截面轴力N1～N4和梁截面剪力V1～V4。对梁柱中心线交点取弯矩平衡获得梁端弯矩M1～M4，以左跨组合梁为例，边柱和失效柱附近的组合梁截面弯矩M1、M2分别为：

式（5）～（6）中，h1、h2分别为水平力H1、H3至H2的距离，a为节点至柱中心线的距离，L为组合梁跨度。

结合式（3）～（6）及隔离体的力学平衡计算，得到试件的关键截面B1、B3、B4、B6处的弯矩发展曲线如图11（a）所示，试件左、右跨组合梁的轴力发展曲线如图11（b）所示。

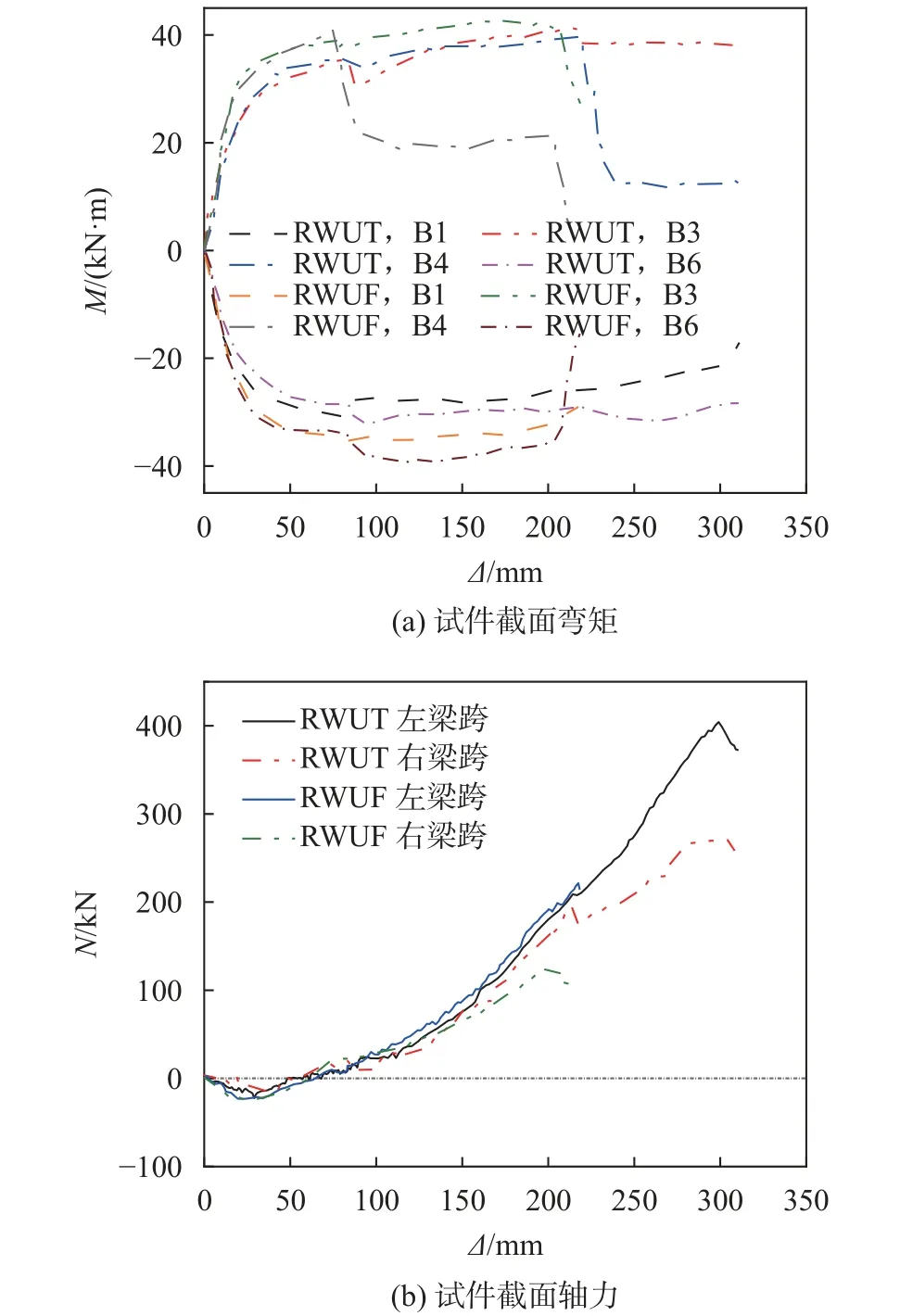
图11 试件内力发展曲线对比Fig.11 Comparison of internal force development curves

由图11（a）可见，试件在形成塑性铰后弯矩基本保持不变，至首次断裂发生时，试件最不利截面处弯矩大幅掉落，同跨远端弯矩稍有增加，相邻跨弯矩基本保持不变。由图11（b）可见，由于压拱效应的影响，轴力在加载前期均为负值，后随位移的增加逐渐过渡为正值并持续发展。试件处于相同的边界环境下，RWUF试件比RWUT试件在非断裂跨轴力略高；对于断裂跨，断裂的发生均使轴力发挥有所停顿。其中，RWUF试件在混合机制阶段前期率先发生断裂，使得混合阶段轴力发挥路径受限，继而影响了加载末期轴力的水平；RWUT试件具备完整的传力截面和良好的变形条件，其总的轴力发挥比RWUF试件更充分。

结合式（1）～（4）可得到两机制的抗力关系发展曲线如图12所示。由图12可见：加载初期，试件抗力几乎完全由梁机制提供，当截面形成塑性铰后，梁机制提供的抗力PM基本保持不变。断裂发生时，PM迅速下降，悬链线机制提供的抗力PN逐步发挥。RWUT试件的首次断裂位移较大，试件轴力已持续、显著发挥，加载结束时，PN超过PM，进入PN主导的抗力阶段；RWUF试件首次断裂位移较小，PN并未充分发挥就丧失了完整的传力截面，加载结束时，其PN水平低于RWUT试件。

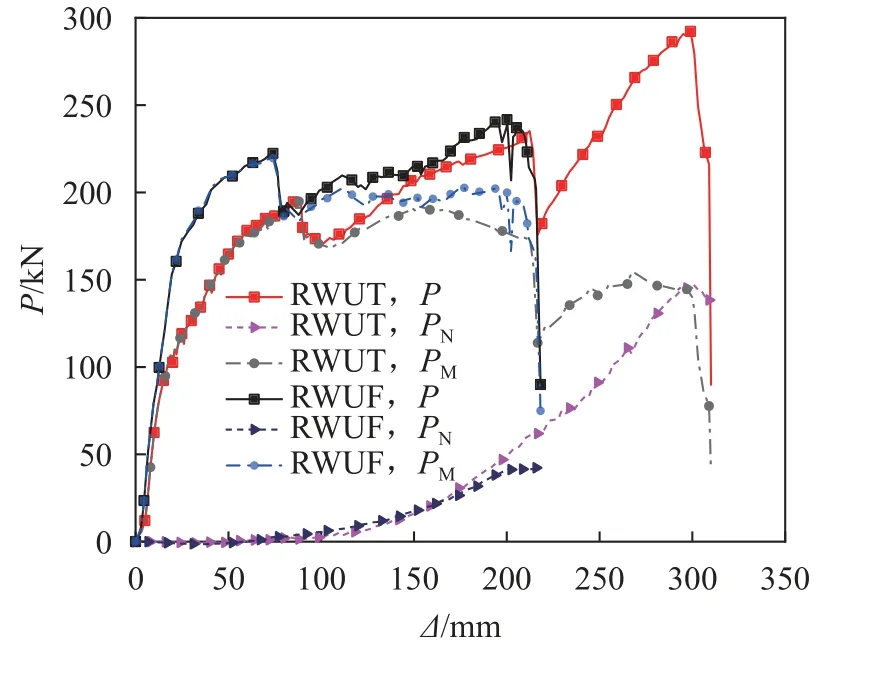
图12 试件抗力机制发展曲线对比Fig.12 Comparison of the development curves of resistance mechanism

3.2 悬链线效应

试件抗力的发展随位移变化是一个动态过程，为进一步评价两抗力机制的动态变化关系，定义梁机制的抗力占比为α，悬链线机制的抗力占比为β，得到二者的表达式为：

式（8）中，i为失效柱处的竖向位移，di为失效柱的竖向位移由0发展至i的距离，PNi为失效柱位移达到i时悬链线机制抗力，Pi为相应位移下的结构总拉力，Ni为相应位移下的组合梁截面轴力。

由式（7）及（8）可知，悬链线效应的发展程度取决于轴力功与总功的比，而轴力功为轴力Ni和轴向伸长量sin θidi的乘积。轴力Ni在混合机制阶段逐渐发挥作用，其水平往往取决于最不利截面处（塑性铰）的转动能力，而轴向伸长量sin θidi，除考虑钢材本身的延伸率外，还可聚焦于部件间的滑移等传力路径的多样化。

试件抗力占比关系如图13所示。由图13可知：试件RWUF在混合机制阶段前期节点处破坏，受力截面被大幅削弱，以致后期轴力发挥受限，悬链线机制的抗力占比较低；试件RWUT在同阶段节点的非线性转动能力更强，这为后期轴力的持续发挥提供了变形条件，充分保证了悬链线机制的迅速发展，至加载结束时，悬链线机制的占比已超过梁机制占比。

图13 试件抗力占比关系对比Fig.13 Comparison of the proportion of resistance

4 动力评估

4.1 动力抗力

结构的连续倒塌本质上是一个复杂的动力过程。由于试验条件和成本等诸多因素的限制，动力试验不便进行。国际上普遍认可Izzuddin等[29]提出的不考虑阻尼作用的能量评估模型评估结构的动力。该模型假定由动力荷载所做的功全部转变为结构的内能，如式（9）和图14所示。根据该假定得到的曲线称为非线性动力响应曲线，并用该曲线初步评估结构是否发生倒塌。

图14 能量评估模型计算方法曲线Fig.14 Calculation curve of energy evaluation model

结合试件静力加载曲线和能量评估模型得到试件动、静力响应曲线如图15所示。由图15可见：两试件在静力卸载前，最大动力荷载值基本一致，而RWUT试件发生了更大的动力位移（310 mm）；若继续加载，其最大动力荷载将继续增大。即处在相同的外部动力荷载条件下，RWUT试件表现出更为优良的变形性能，具备更为充足的抗倒塌能力储备。

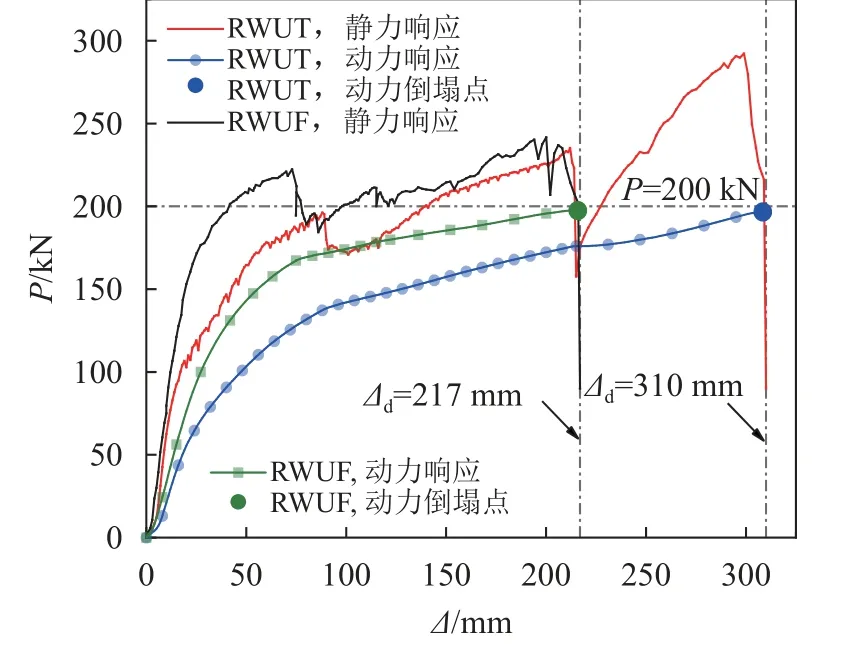
图15 试件动、静力响应曲线Fig.15 Dynamic & static response curve of specimens

4.2 动力效应

为更加直观地反映结构静、动力荷载之间的关系，工程设计常以动力放大系数KDIF修正结构静力计算获得的倒塌抗力[30]。该系数为结构静、动力荷载的比值，满足式（10）。

KDIF越大，表明结构所能承担的动力荷载相对于结构自身所能承担的静力荷载越小。同时，DOD[1]指南给出的动力放大系数KDOD计算式为：

式中，θcby为组合梁端屈服转角，θcby=Wcbpfcbylcb/6EcbIcb，由文献[13]给出的计算式获得，其中，Wcbp为组合梁塑性截面模量，fcby为组合梁的屈服强度，lcb为组合梁跨度，Ecb为组合梁换算截面惯性矩，Icb为组合梁截面惯性矩，θpra为组合梁端塑性转角。

两试件动力放大系数曲线如图16所示。

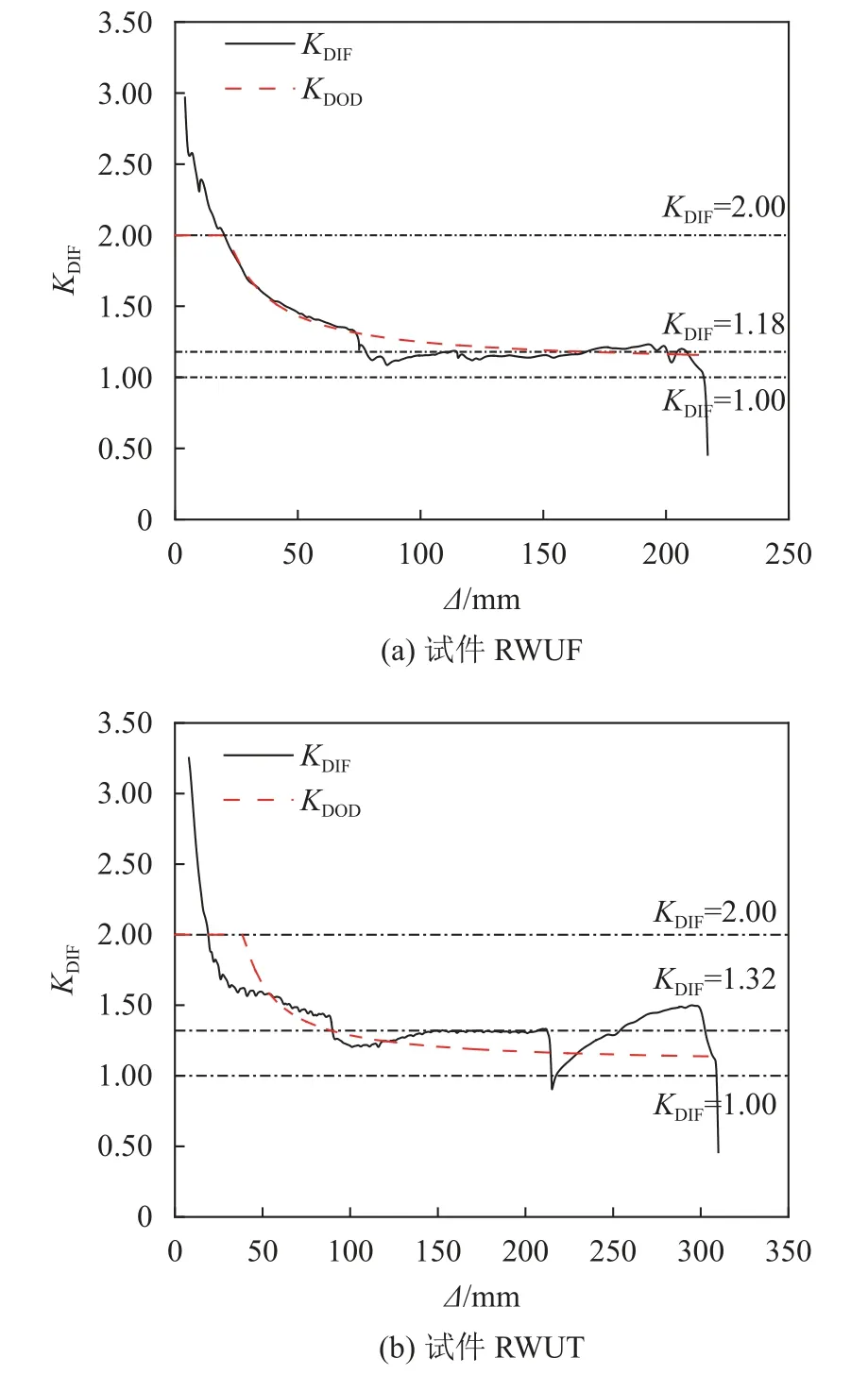
图16 两试件动力放大系数曲线Fig.16 Curves of dynamic amplification factors of two specimens

由图16可见，在初始弹性、压拱阶段，试件的KDIF值均由最大值迅速回落至相对稳定的状态，这与结构在突遇动荷载情形下的结构动力响应由瞬时最大后回落趋势一致。RWUF试件的KDIF曲线在趋势稳定前因断裂而突降并最终稳定在1.18左右；RWUT试件的KDIF曲线在首次断裂前稳定在1.32左右，断裂后曲线回升直至加载结束。相对于RWUT试件，RWUF试件动力放大系数更小的原因是，其早期断裂特征导致结构的悬链线抗力无法充分发挥（静力倒塌抗力断后始终处于较低水平），其动力倒塌抗力的发展因结构连续发生断裂被抑制，这将对结构持续抵抗动载产生不利影响。保证节点在弹性、压拱以及混合机制阶段具备持续的转动能力，是结构静力荷载不断提高的必要条件，也是切实提高结构动力倒塌抗力的前提。

5 结 论

1）试件倒塌全过程可分为弹性阶段、压拱阶段和混合机制阶段。节点具有优良的非线性转动能力和荷载具备传递路径是结构抗力不断发展的主要原因。

2）试件的断裂均发生在梁段拼接处，有效保护了梁柱节点核心区的受力性能。RWUT试件形式比RWUF试件形式具备更加优良的节点非线性转动能力，在相同的抗力需求下，具备更加充足的变形储备。

3）在相同的边界环境下，RWUF试件具备更大的初始刚度，可在较小位移下终止倒塌；RWUT试件螺栓的有限滑移和螺栓孔壁的轴向变形有利于结构悬链线机制抗力的发展，其构件性能的发挥更加充分。

4）由动力分析结果可知，节点在结构倒塌全过程具备可靠的转动能力是结构静力荷载不断提高的必要条件，RWUT试件结构优于RWUF试件结构的动力抗倒塌能力。