分离式复合土工膜鼓胀变形的膜布复合规律

薛 霞，李旺林*，卫如春，杨 哲，韩瑞晨，汪万升

(1.济南大学 水利与环境学院，山东 济南 250022；2.山东大学 海洋研究院，山东 青岛 266237)

土工合成材料广泛应用于大面积防渗工程中，包括闸、坝、水库等水利工程，垃圾填埋场、污水处理池等环境工程，路桥、护岸以及地下工程等[1-2]，有极好的防渗效果。土工膜是工程防渗的核心，在一些重要工程中，为了保护核心土工膜不受损伤，通过热融合或黏结作用形成的结合式复合土工膜和土工膜/布分别铺设的分离式复合土工膜得到了广泛的应用[3-4]。其中，分离式复合土工膜既避免了结合作用对土工膜产生的损伤，也可以保护中间土工膜，因而更适合在平原水库全库盘水平防渗工程中使用[5]。目前较为常用的是两布一膜分离式复合土工膜[6]。不过，分离式复合土工膜铺好后，其中的土工膜截断了上下层之间的水气交换通道。当膜下工程条件发生改变引起气体聚集、压缩而使压力增大时[7-8]，分离式复合土工膜会产生气胀甚至胀破的问题[9-10]。

由于实际气胀现象多表现为近似半球形，因此现有很多研究将气胀问题概化为环向约束球形鼓胀变形问题[11-12]，即球形变形假设。本文采用了这一假设，其涉及的主要参数包括球形内部的鼓胀压力、鼓胀高度以及鼓胀直径。在此基础上，利用球体的垂向受力平衡或薄壁容器压力理论以及几何关系可以进行鼓胀变形的应力-应变分析与计算[13-14]。再结合室内环形夹具进行鼓胀变形试验，即可研究不同因素（如夹具尺寸、材料厚度、加载速率和温度等[15-16]）对材料鼓胀变形和强度的影响。

单层土工膜、结合式复合土工膜的鼓胀变形基本都是整体性的，可以采用上述方式进行材料鼓胀变形力学特性的研究[12,17]。但分离式复合土工膜是由基础的土工膜、土工布组合起来的层状复合材料，在发生鼓胀变形时，Andrejack[15]、薛霞[3]、普勇柽[18]等分别对土工膜+垫层、上布下膜分离式复合土工膜鼓胀变形力学特性进行了试验研究，得出层状材料分别有各自的作用[19]，复合材料整体的鼓胀压力近似为层状材料的鼓胀压力之和。从力学分析角度而言，层状复合材料单向拉伸时，根据轴向受力平衡，复合材料轴向力为各层材料受力之和，复合材料力学中的混合定则（mixing rules）也表明复合材料的力学性能和物理性能主要取决于组成复合材料的材料组分和其体积百分比[20]。然而，鼓胀变形与平面单向拉伸变形不同，各层材料受法向压力弯曲变形，目前对其变形特性、作用和影响的研究很少，各层材料的复合作用规律尚不清楚。

本文以分离式复合土工膜材料为基础，采用自主设计的高强度土工合成材料鼓胀变形试验设备，通过分离式复合土工膜的室内鼓胀变形试验和复合材料力学分析，进行分离式复合土工膜鼓胀变形力学特性的膜布复合规律研究，以明确层状复合材料在发生鼓胀变形时各层材料的作用及影响规律，进一步补充完善该方面的理论研究，同时也为实际应用中分离式复合土工膜鼓胀变形力学特性的确定和材料的选择提供一定的参考。

1 室内鼓胀变形试验

1.1 试验设备

采用的高强度土工合成材料鼓胀变形试验仪，是在已有鼓胀变形试验相关设备[16-17]和胀破试验相关标准[13,21]的基础上经过一定研发和改进而完成的。图1为试验仪器示意图，由基础平台、测量系统和加载系统3个部分组成。

图1 鼓胀变形试验仪器示意图Fig.1 Test apparatus for bulging deformation

图1中，基础平台由不锈钢法兰盘组、操作平台和控制平台组成。其中：上、下法兰盘均为不锈钢圆环，其内径分别为100、200 mm，为试样提供环向约束，形成密闭空间，保证试样在承受压力时发生球形鼓胀变形。控制平台上有控制按钮和显示器，前者用于控制加载系统的启动、停止和加载模式；后者与压力传感器连接，显示压力变化过程。

测量系统由数显压力传感器、激光位移传感器和高清录像系统组成。其中，数显压力传感器记录试样鼓胀变形时的鼓胀压力和时间，激光位移传感器记录试样鼓胀变形时的鼓胀高度，高清录像设备与计算机连接并实时记录试样的鼓胀变形及破坏特征、鼓胀压力和鼓胀高度。

加载系统由三相异步电机、液压泵、连杆、液缸和高压胶管组成。在试验过程中加载系统通过高压胶管向基础平台上的试样下方提供持续稳定的压力，可以通过控制平台调节其加载速率。

1.2 试验材料

选择HDPE土工膜（简称土工膜或膜，用M表示）和短纤针刺无纺土工布（简称土工布或布，用T表示）为基础材料，组成两布一膜式分离式复合土工膜（250 g·m2/HDPE0.4 mm/250 g·m2，用TMT表示）。基础材料的力学指标见表1。根据设备内径的大小裁剪试样，裁剪出的试样如图2所示。

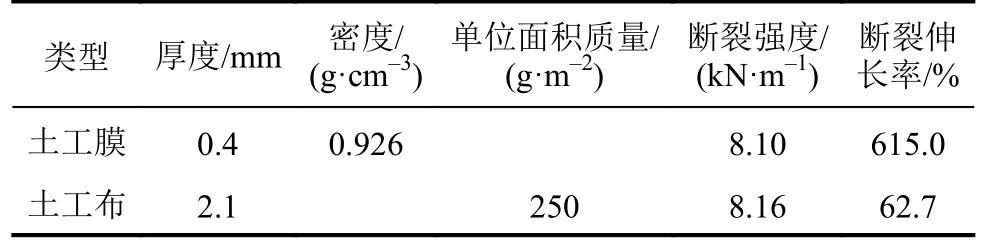
表1 试验材料基本力学指标Tab.1 Properties of the test materials

图2 试验材料照片Fig.2 Photographs of the test materials

1.3 试验方法

试验选用两布一膜分离式复合土工膜进行鼓胀变形试验。基础材料即单层土工膜（M）、单层土工布（T）作为对照组进行鼓胀变形试验。由于单层土工布具有透水性，在其下方设置垫层进行试验，并对数据进行校正处理[15,21-22]。

由于环形法兰盘直径为200 mm时，分离式复合土工膜的鼓胀变形特征更加明显，且其需要的加载压力更小，因此试验中采用直径为200 mm的环形法兰盘进行鼓胀变形试验，加载速率为100 mL/min。

试验过程中，首先根据夹具直径裁剪试样；其次，将加载系统的承压部件（液缸和高压胶管）充满水直至试样底部，以确保整个加载系统内具有均匀的压力；之后，通过螺栓和密封胶圈将试样固定在两个法兰之间；随后，试样的鼓胀压力和鼓胀高度校准后开始加载测试过程中加载压力均匀上升，试样在加载压力作用下向上鼓起变形直至破坏。

1.4 应力-应变计算

通过测量系统得到试样鼓胀变形的鼓胀压力和鼓胀高度后，可以采用基于球形假设和体积不变假设推导得到的公式计算材料应力σ[23]：

式中：σ为应力，N·mm-2；P为鼓胀压力，MPa；h为鼓胀高度，mm；d为夹具直径，mm；δ为试样厚度，mm。

线性伸长一般为单轴拉伸变形，而鼓胀变形可认为是多轴拉伸变形。试样未鼓胀变形时为平面圆形，鼓胀变形后为3维球形，面积增加。因此，以多轴拉伸变形中的面积增加率，即试样鼓胀变形后产生的面积增量与未变形时的面积的比值[24]来表达应变ε：

式中，ε为球形鼓胀变形产生的应变，%。

2 复合材料鼓胀变形力学分析

为了研究鼓胀变形时分离式复合土工膜中土工膜和土工布对分离式复合土工膜整体鼓胀压力和应力的作用规律，将分离式复合土工膜视为一种受环向约束和内部垂直于材料平面的法向压力P而发生球形鼓胀变形的复合材料，如图3所示。图3中：T为张拉力，N·mm-1；TC和Ti分别为复合材料整体和各层（以i层表示）材料截面受到的张拉力，N·mm-1。

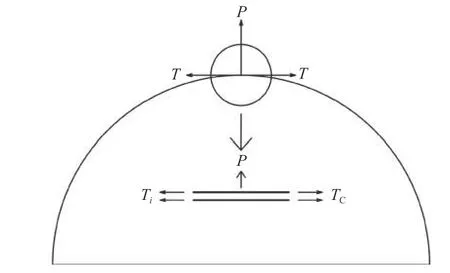
图3 复合材料球形鼓胀变形力学分析示意图Fig.3 Schematic diagram of mechanic analysis for spherical bulging deformation of composite materials

2.1 分离式复合土工膜的鼓胀压力计算

根据垂向受力平衡，可以得到材料法向压力P与变形曲面张拉力T的关系[11]为：

令k=(d2+4h2)/(16h)，则以变形系数k（与夹具直径d和鼓胀高度h相关）和鼓胀压力P表示材料的张拉力为：

土工膜表面光滑，其与土工布组成的复合材料的层间相互作用很小，因此暂不考虑层间力的作用[25-26]，则根据结构张拉方向的力平衡（图3），对复合材料单位宽度上的某一截面受力，有：

将式（4）代入式（5），并分离变量，得到复合材料的鼓胀压力计算式：

式中：kC和ki分别为复合材料鼓胀变形过程中整体和各层（以i层表示）的变形系数k，mm；PC和Pi分别为复合材料鼓胀变形过程中整体和第i层的鼓胀压力，MPa。

式（6）中，分离式复合土工膜最下层的土工布由于透水性无法承担鼓胀压力，即相应的鼓胀压力近似为0。其上方膜布结构的d和h在变形过程中可认为是近似相等的，有ki=kC，因此有：

式（7）说明分离式复合土工膜整体的鼓胀压力为上方膜、布材料在相同鼓胀高度时的鼓胀压力之和。利用基础材料，即单层土工膜和单层土工布的试验数据作为计算基础，采用式（7）计算得到分离式复合土工膜的鼓胀压力-鼓胀高度计算值并绘制相应的曲线，如图4所示。

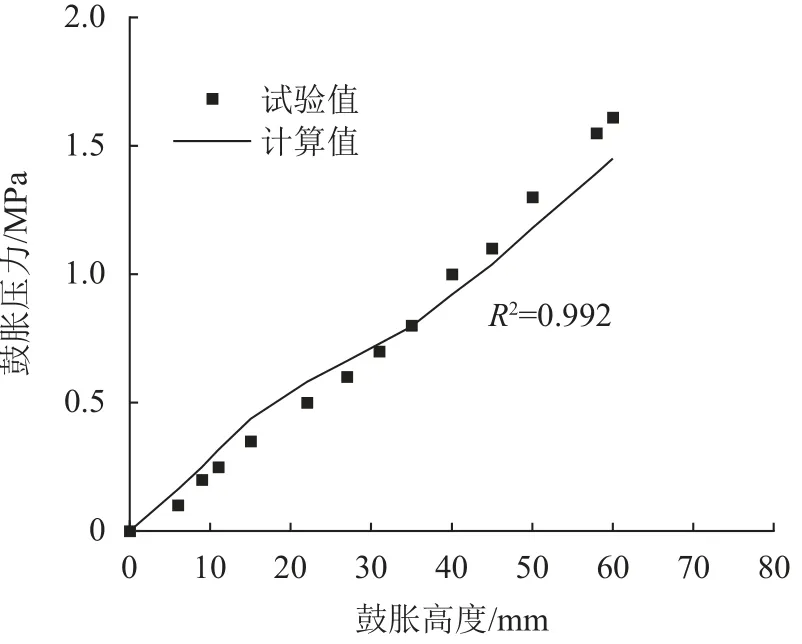
图4 鼓胀压力的试验值和计算值对比Fig.4 Comparison between the test and calculation values for the bulging pressure

从图4可知，鼓胀压力的计算值和试验值曲线较吻合，其判定系数R2为0.992，得出鼓胀压力计算公式是较为准确合理的。

2.2 分离式复合土工膜的应力计算

对于发生鼓胀变形的材料（不考虑未发生鼓胀变形的最下层土工布），根据薄壁理论，当材料的厚度较薄时，可假设其截面内产生的应力沿厚度均匀分布，则以截面厚度和应力表达的张拉力为：

将式（8）代入式（5），并分离变量，得到复合材料的应力计算式为：

式中：δC和δi分别为复合材料鼓胀变形过程中整体和第i层的厚度，mm；σC和σi分别为复合材料鼓胀变形过程中整体和第i层的应力，N·mm-2。

将通过式（1）和式（2）计算得到单层土工膜和单层土工布的应力-应变数据作为计算基础，代入式（9）得到分离式复合土工膜的应力-应变计算值并绘制相应的曲线，如图5所示。

图5 应力的试验值和计算值对比Fig.5 Comparison between the test and calculation values for the stress

由于材料的物理性质、纤维分布、局部空隙和微裂纹等都会影响复合材料的强度，简化的理论分析较难全部考虑这么多复杂的因素[20]，因此复合材料的计算值和试验值曲线有一定的偏差。不过，整体而言，应力-应变计算值和试验值曲线较吻合，判定系数R2为0.887，得出应力计算公式也是较为准确合理的。

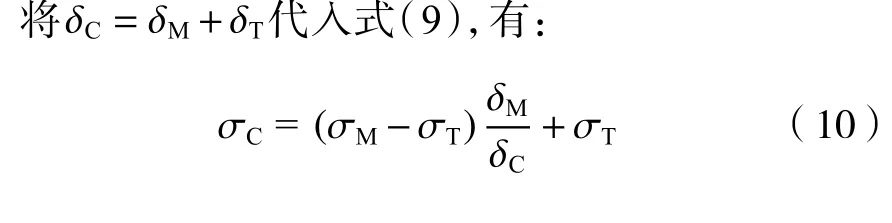
式中：δM和δT分别为复合材料鼓胀变形过程中土工膜层和土工布层的厚度，mm；σM和σT分别为复合材料鼓胀变形过程中土工膜层和土工布层的应力，N·mm-2。

3 结果及分析

3.1 鼓胀变形及破坏特征

土工膜M、土工布T和分离式复合土工膜TMT的鼓胀变形及破坏特征如图6所示。由图6可见，试样在鼓胀压力的作用下膨胀变形，形成并维持球冠状，直至在冠顶中心处形成点状或线状撕拉破坏。

图6 土工膜、土工布和分离式复合土工膜鼓胀变形及破坏特征Fig.6 Deformation and failure characteristics of geomembrane, geotextile, and separated composite geomembrane

土工膜先在冠顶附近产生裂纹，裂纹处土工膜变薄变透明，并在裂纹垂直方向拉伸变形，变形一定程度之后冠顶处突然产生裂口并破坏；土工布维持球冠状变形，直到冠顶处突然出现点状或线状撕拉的裂口破坏。由于透水性，分离式复合土工膜最下层土工布微小鼓胀后不再变化，而上层膜布结构继续发生鼓胀变形，最上层土工布延伸率较低，因此其先于下层土工膜破坏，土工布破坏后压力完全由土工膜承担，使得土工膜也瞬间破坏，因此二者裂口位置基本相同，都在冠顶附近，压力介质从裂口处喷出。

3.2 鼓胀压力的膜布复合规律

3.2.1 鼓胀压力的无效层和有效层分析

压力加载后，分离式复合土工膜中最下层与压力介质接触的土工布层并没有发生变形或破坏。土工布是透水性材料，初始加压时，最下层的土工布对压力介质有微弱的阻挡作用，能承担很小的压力并发生微小变形；当压力介质透过的空隙形成并稳定，下层土工布基本不再变化；压力介质继续作用于上层膜布结构使其不断产生鼓胀变形直至破坏。

为进一步明确最下层土工布的鼓胀变形效应，进行了一布一膜（上布下膜，MT）分离式复合土工膜的鼓胀变形试验，并与两布一膜分离式复合土工膜（TMT）的鼓胀压力进行比较，结果如图7所示。经统计，MT与TMT的鼓胀压力的差别在±0.07 MPa以内，十分微小，且MT与TMT的曲线整体上十分接近，说明分离式复合土工膜中最下层的土工布基本没有鼓胀变形作用。

图7 MT和TMT的鼓胀压力-鼓胀高度关系曲线比较Fig.7 Comparison of bulging pressure and bulging height of MT and TMT

因此，可以认为分离式复合土工膜中最下层与压力介质接触的土工布是一种鼓胀变形无效层，而上层的膜布结构则为鼓胀变形有效层。分离式复合土工膜鼓胀变形有效层数是少于实际层数的。不过，需要注意的是，由于最下层土工布在实际应用中往往发挥防刺破、排水排气等作用，因此上述有效层和无效层仅指其鼓胀变形方面的特性。

3.2.2 鼓胀变形中的膜、布鼓胀压力作用规律

通过测量系统可以得到试样发生鼓胀变形时，不同鼓胀高度对应的鼓胀压力关系曲线如图8所示。

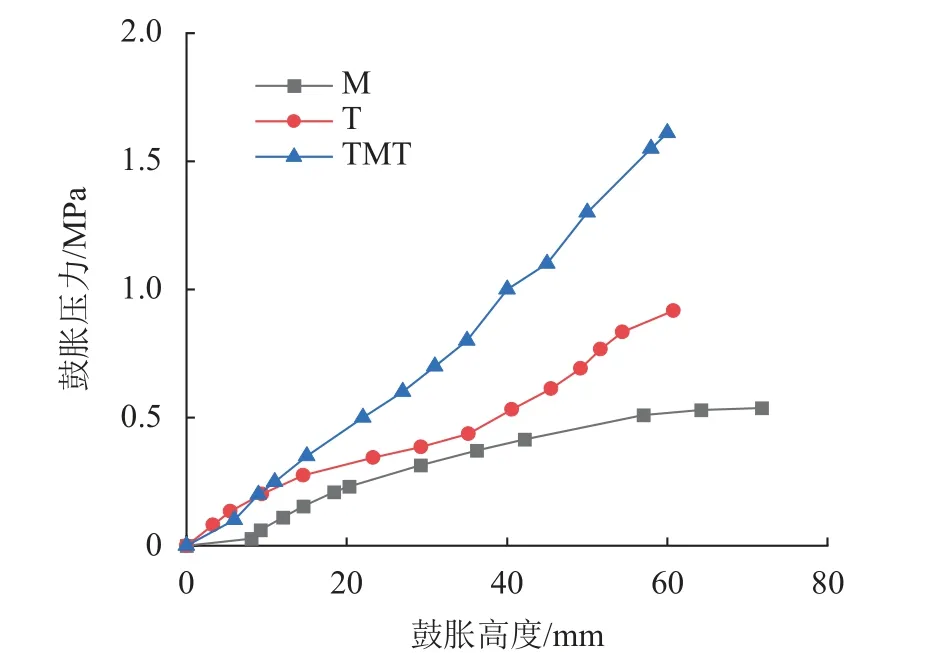
图8 试样鼓胀变形的鼓胀压力-鼓胀高度关系曲线Fig.8 Curves of bulging pressure and bulging height for samples

从图8可看出，相同鼓胀高度时，分离式复合土工膜的鼓胀压力最大，土工膜的鼓胀压力最小，土工布居中。曲线趋势上，随鼓胀高度的增加，鼓胀压力增加，其中，分离式复合土工膜的关系曲线基本为线性变化，土工膜的关系曲线为非线性变化，而土工布的关系曲线则近似线性变化。

由于最下层土工布为鼓胀变形无效层，因此，结合式（7）可知，分离式复合土工膜的鼓胀压力值基本为一层土工膜和一层土工布在相同高度时的鼓胀压力之和，即分离式复合土工膜的鼓胀压力为结构中有效层的鼓胀压力之和。该规律与Andrejack[15]和薛霞[3]等根据试验结果提出的膜布共同作用的求和规律基本一致。

3.2.3 鼓胀破坏时的膜、布胀破压力和胀破高度作用规律

由图8可知，分离式复合土工膜的胀破压力大于土工布或土工膜的胀破压力。由于最下层土工布为鼓胀变形无效层，尽管分离式复合土工膜由两布一膜组成，但其整体胀破压力近似于一层土工布和一层土工膜的胀破压力之和。同时，由于上层土工布胀破之后土工膜才破坏，因此应取土工布胀破高度对应的土工膜的鼓胀压力为计算基础。当土工布胀破时，土工膜很快胀破，且其鼓胀压力变化较小、趋于稳定，则取其胀破压力为计算基础也可满足要求。

分离式复合土工膜的胀破高度与土工布的胀破高度近似相等，且都小于土工膜的胀破高度。当复合材料最上层的土工布达到其胀破高度而突然破坏时，其破坏处承担的压力瞬间由附近的土工膜承担。根据图8可知，土工膜此时承担的压力为分离式复合土工膜的整体压力，远大于土工膜本身的胀破压力，因此土工膜也会在相近位置瞬间破坏，这也意味着分离式复合土工膜整体破坏。因此，分离式复合土工膜与土工布的胀破高度近似相等。

3.3 应力的膜布复合规律

3.3.1 应力的无效层和有效层分析

由于最下层土工布未发生鼓胀变形，其鼓胀压力和鼓胀高度都近似为0，根据式（1）和式（2）计算得到相应的应力和应变也为0。因此，最下层土工布在应力作用方面也为无效层。相应地，上方的膜布结构为有效层。

3.3.2 鼓胀变形中的膜、布应力作用规律

根据式（1）和式（2）计算得到试样鼓胀变形的应力和应变，其关系曲线如图9所示。由图9可知，应力-应变曲线包括线弹性、屈服、强化和胀破阶段[3,12]。线弹性阶段，土工布的弹性模量最大，土工膜最小，分离式复合土工膜居于二者中间，且较为接近土工膜的曲线，说明鼓胀变形初期，分离式复合土工膜的变形主要由土工膜承担；屈服阶段，由于土工布的低延伸率产生的约束作用，土工布也开始承担一定的鼓胀变形作用，且分离式复合土工膜随着土工布材料的屈服而产生屈服。由于试验过程中屈服阶段极不稳定，因此其数值小于土工布的屈服强度（图9）。根据式（9）和图5中屈服阶段曲线的对比可知，分离式复合土工膜的屈服强度与土工布的屈服强度是近似相等（约为30 N/mm2）；在强化阶段，相同应变时，由于土工布纤维空隙较多，其应力最小，单层土工膜应力最大，而分离式复合土工膜的应力-应变关系曲线位于单层土工膜和单层土工布之间。

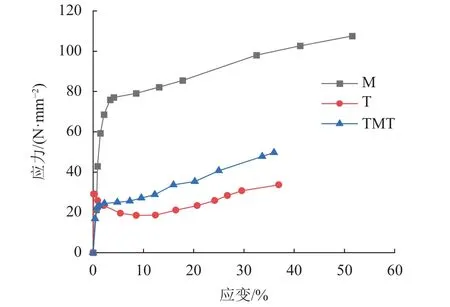
图9 试样鼓胀变形的应力-应变关系曲线Fig.9 Curves of stres and strain for bulging samples

整体上，分离式复合土工膜的应力值总是处于各层材料本身的应力值之间。根据式（9），δi/δC可视为复合材料第i层材料的厚度百分比，则复合材料的应力与相同应变时各层材料本身的应力和其厚度百分比正相关，基础材料的应力越大，所组成的复合材料应力也越大；同时，某一种材料的厚度百分比越大，复合材料的应力也越接近该材料的应力，如图10所示。结合式（10），其接近的快慢程度还与基础材料本身之间的应力差有关，差值越大，其接近程度越快。

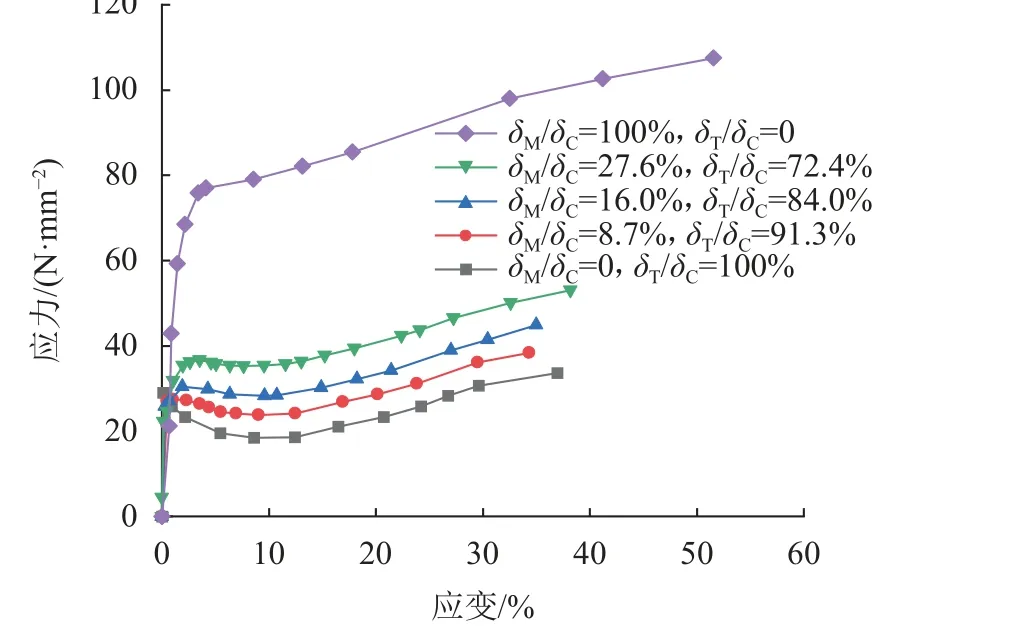
图10 复合材料应力与各层材料应力、厚度百分比的关系Fig.10 Relationship between composite material stress and each effective layer’s stress and thickness percentage

另外，式（9）中δiσi/δC也可视为第i层材料应力对复合材料整体应力的贡献作用，则复合材料鼓胀变形时的整体应力可视为各层材料应力的贡献作用之和，且各层材料应力贡献作用的比例为该材料的厚度百分比，贡献作用的大小为其本身应力与其厚度百分比的乘积。极端情况下，当第i层材料的厚度百分比为100%，即复合材料全部由一种材料组成时，复合材料的应力全部由该层材料贡献，其数值与该材料应力值一致。

3.3.3 鼓胀破坏时的膜、布胀破应力和胀破应变作用规律

由图9可知，分离式复合土工膜的胀破应力位于土工膜和土工布之间，接近土工布的胀破应力，其数值大小可通过式（9）获得。由于分离式复合土工膜的胀破高度接近土工布的，而土工布到达胀破应变时，土工膜还未胀破，其应力仍随着应变的增加而增加，因此计算中应取土工布胀破应变处对应的土工膜的应力，而非其胀破应力。

与分离式复合土工膜的胀破高度作用原理类似，当土工布产生破坏时，复合材料整体的鼓胀压力远大于土工膜能够承担的压力，因而在其截面上产生远大于相同应变时其能承受的应力，使土工膜发生破坏。因此，分离式复合土工膜的胀破应变也与土工布的胀破应变近似，且都小于土工膜的胀破应变。

4 膜布复合规律的应用

目前，对于分离式复合土工膜材料的鼓胀变形强度，工程实用上基本依靠试验方法测定[20]。本文通过室内试验和力学分析方法得到了分离式复合土工膜鼓胀变形的膜布复合规律。利用该理论规律可以确定复合材料鼓胀变形的力学特性，明确基础材料性能对复合材料鼓胀变形强度的影响，进而为复合材料选型设计提供参考。该规律应用于新疆阿克苏地区某平原水库全库盘复合土工膜的选型设计中，为工程设计与建设提供了很大的帮助。

4.1 分离式复合土工膜的鼓胀变形力学特性

当已知不同厚度土工膜和不同单位面积质量土工布的鼓胀变形力学特性（主要是指鼓胀压力-鼓胀高度曲线和应力-应变曲线）时，即可根据上述室内试验和理论计算公式，得到不同厚度土工膜和不同单位面积质量土工布组成的不同分离式复合土工膜鼓胀变形及破坏的力学特性，包括其变形及破坏特征、鼓胀压力-鼓胀高度曲线和应力-应变曲线等。在新疆阿克苏地区某平原水库库盘复合土工膜的选型设计中，首先根据工程基本情况，初步选定拟采用的不同厚度的土工膜材料M1、M2、M3和不同单位面积质量的土工布材料T1、T2、T3，之后通过室内试验得到拟采用基础材料的鼓胀变形力学特性，再通过膜布复合规律即可得到T1M1T1、T1M2T3以及T3M2T1等各种不同组合方式的分离式复合土工膜（用A、B、C等字母表示）的鼓胀变形力学特性，极大地方便了复合材料鼓胀变形力学特性的初步确定。

4.2 分离式复合土工膜材料选型的安全性分析

通过上述方式得到不同种分离式复合土工膜鼓胀变形的应力-应变曲线后，可以利用曲线交会法或数值模拟等方法计算得到某一工况下的工作应力和工作应变[27]，再依据公式S=F1/F2（S为安全系数，F1为胀破应力（或胀破应变），F2为工作应力（或工作应变））计算得到不同种分离式复合土工膜在工程应用状态下产生鼓胀变形时的应力安全系数（或应变安全系数）。不同组合方式的分离式复合土工膜（A～J等）的安全系数及依据安全系数进行选型的安全性分析如图11所示。图11中，Sg为工程需要的鼓胀变形安全系数，灰色区域为满足该工程鼓胀变形安全性要求的所有分离式复合土工膜材料。如此，可以扩展工程可选材料的范围，提高工程选材的效率，助力工程设计和建设工作。

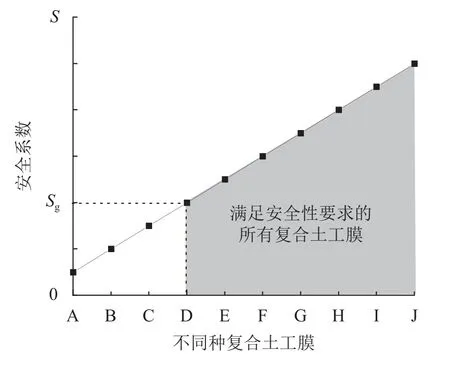
图11 材料选型的安全性分析Fig.11 Safety analysis of material selection

5 结 论

本文采用室内试验和理论分析方法，研究了分离式复合土工膜鼓胀变形力学特性的膜布复合规律。结论如下：

1）分离式复合土工膜发生鼓胀变形时，与压力介质接触的最下层土工布为鼓胀变形无效层，基本不产生变形，上层膜布结构为鼓胀变形有效层。有效层中最上层土工布首先发生裂口型破坏，土工布破坏后土工膜也会瞬间破坏。

2）根据鼓胀压力的膜布复合规律，分离式复合土工膜的鼓胀压力（含胀破压力）为各有效层在相同鼓胀高度时的鼓胀压力之和，其胀破高度与土工布的胀破高度近似相等。

3）根据应力的膜布复合规律，分离式复合土工膜鼓胀变形的应力-应变曲线位于土工膜和土工布的应力-应变曲线之间，其应力（含胀破应力）等于有效层膜、布在相同应变时的应力与其厚度百分比的乘积之和，其胀破应变与土工布胀破应变近似相等。另外，有效层土工膜/布材料本身的应力越大，所组成的复合材料应力也越大；某一材料厚度百分比越大，复合材料应力越接近该材料的应力值，且接近的快慢程度与有效层材料之间的应力差值大小成正比。

4）对于不同规格、类型基础材料组合成的不同种分离式复合土工膜，研究结果有助于确定其鼓胀变形力学特性，并为材料选型提供参考。