可控磁路永磁悬浮带式输送机支撑系统研究

胡 坤，钱王钱，蒋 浩，杨金晗，朱勤勤

(1.安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室，安徽 淮南 232001；2.安徽理工大学 环境友好材料与职业健康研究院，安徽 芜湖 241000；3.安徽理工大学 机械工程学院，安徽 淮南 232001)

带式输送机是目前世界上使用范围最广、最为重要的散状物料连续运输设备之一，具有输送距离长、运量大、可连续输送、易实现自动化控制等特点，被广泛应用于煤炭、电力、物流、建材等国民经济各个行业。传统带式输送机由输送带承载物料并由托辊进行支撑，在运行过程中，托辊在输送带的挤压接触下克服轴承旋转阻力。旋转阻力看似微小，但对于大型带式输送机，沿程托辊数量惊人，积聚的旋转阻力成为带式输送机的主要阻力，与托辊相关的能量消耗甚至达到整个输送机系统总能耗的70%[1]。而磁悬浮带式输送机是一种利用磁悬浮技术[2-4]作为支撑方式的新型低阻力带式输送机，可从根本上解决托辊的旋转能耗问题，兼具带速快、噪声低、减振性好，环保性高等特点，经济价值和实用前景巨大。

目前磁悬浮支撑方式主要有永磁悬浮[5-6]、电磁悬浮[7-9]及混合磁悬浮[10-12]。永磁悬浮结构简单、低能耗、成本低，但其气隙和姿态不易调节；电磁悬浮和混合磁悬浮稳定性高，但由于涉及电磁结构，线圈易发热产生较高能耗，控制系统复杂。不同于以上磁悬浮支撑方式，可控永磁悬浮兼具可控性与永磁悬浮的优点，同时避免了电磁发热能耗问题，得到国内外学者的广泛关注。韦伟等[13]针对一种永磁悬浮回转系统的回转特性进行分析，验证盘状永磁铁的磁场特性和铁球的磁化特性，并确定系统中永磁铁相对最优的布置方式；金俊杰等[14]设计了一种永磁悬浮无尘传送系统，采用两对双列对称布置的非接触主动永磁悬浮支撑，通过改变悬浮支撑与导轨间的磁通量实现对悬浮力的实时控制；Oka等[15]提出一种非接触式旋转系统，利用垂向永磁铁实现小球稳定悬浮，分布于周围的永磁铁控制小球的旋转，并分析其扭矩特性；Mizuno等[16]提出一种新型磁悬浮系统，通过改变进入永磁体与悬浮物体间铁磁板的长度，实现小球的悬浮控制。以上研究对可控永磁悬浮技术做出巨大贡献，主要涉及可控永磁悬浮技术的磁力控制方式、系统建模、结构优化等方面，但在可控永磁悬浮带式输送机方面研究较少，特别是由于带式输送机本身独特的结构特点，还存在柔性输送带变形影响稳定悬浮、输送带物料应力响应干扰等问题亟待解决，限制了可控永磁悬浮技术在低阻力带式输送机领域的应用。

为此，本文提出一种可控永磁支撑系统，通过可控永磁技术实现托辊悬浮支撑，利用可控永磁斥力实现托辊位置的调节。系统通过控制安装在导磁体内的双径向永磁体，调节导磁体内部磁路，使得导磁体两端产生变化磁场并与固定于托辊轴两端圆周上的永磁贴片相互作用，进而控制托辊悬浮气隙与姿态。基于系统原理与性能，在综合考虑系统漏磁特性的基础上，建立单点系统参数化模型，分析其动力学特性，并进行系统控制研究。

1 工作原理

可控磁路永磁悬浮带式输送机结构如图1所示，上托辊采用可控永磁支撑装置，下托辊采用普通回程托辊。输送机运行过程中，可控永磁支撑装置可根据物料运输工况对悬浮气隙进行调整；在输送带发生跑偏时，通过调整悬浮气隙改变输送带左右两侧托辊高低姿态实时调偏；输送带回程无物料输送，为了节约成本采用普通回程托辊。

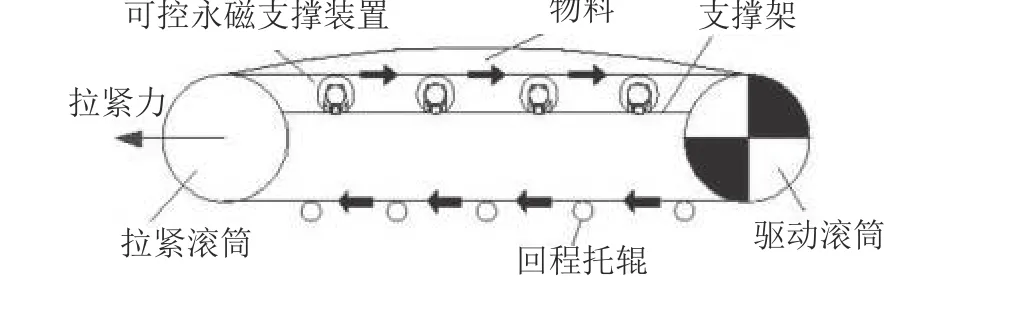
图1 可控磁路永磁悬浮带式输送机Fig.1 Controlled magnetic circuit permanent magnetic suspension belt conveyor

可控永磁支撑装置主要结构如图2所示，该装置由两个径向永磁体（永磁体黑色为N极，白色为S极），导磁体，托辊、永磁贴片及与两个径向永磁体相连的电机（图2中未示出）组成。双径向永磁体安装在导磁体内，通过控制旋转径向永磁体可以调节径向永磁体在导磁体内的磁路，从而使导磁体两端产生变化磁场并与固定于托辊轴两端圆周上的永磁贴片相互作用实现悬浮。系统通过调节径向永磁体和永磁贴片之间的磁斥力来克服载荷，进而控制托辊悬浮气隙和姿态。

图2 可控永磁支撑装置Fig.2 Controlled permanent magnet support device

2 单点系统设计分析

由于仿真实验优化方法具有速度快、便于使用等优点。为此，采用Maxwell仿真软件对单点可控永磁支撑系统进行结构优化分析，其中，永磁体材料采用NdFeB35，剩磁为1.18 T，矫顽力为868 kA/m，导磁体材料为硅钢（牌号为50W540）。钕铁硼永磁材料作为第3代稀土永磁材料，因具有较高的剩磁、矫顽力、价格相对较低、易于加工等优势被广泛使用；硅钢是一种硅铁软磁合金，具有导磁率高、矫顽力低、加工工艺成熟、价格低等特性。因此，永磁体、导磁体材料分别采用钕铁硼及硅钢。

2.1 优化导磁体斜端面角度

为了选择合适的导磁体斜端面角度，对导磁体斜端面不同角度下的磁感应强度进行分析。考虑系统对称性，在仿真软件中设置以垂直于左边导磁体腿部斜端面中点处磁感应强度为参考点，固定转动角度为90°，分析结果如图3所示。

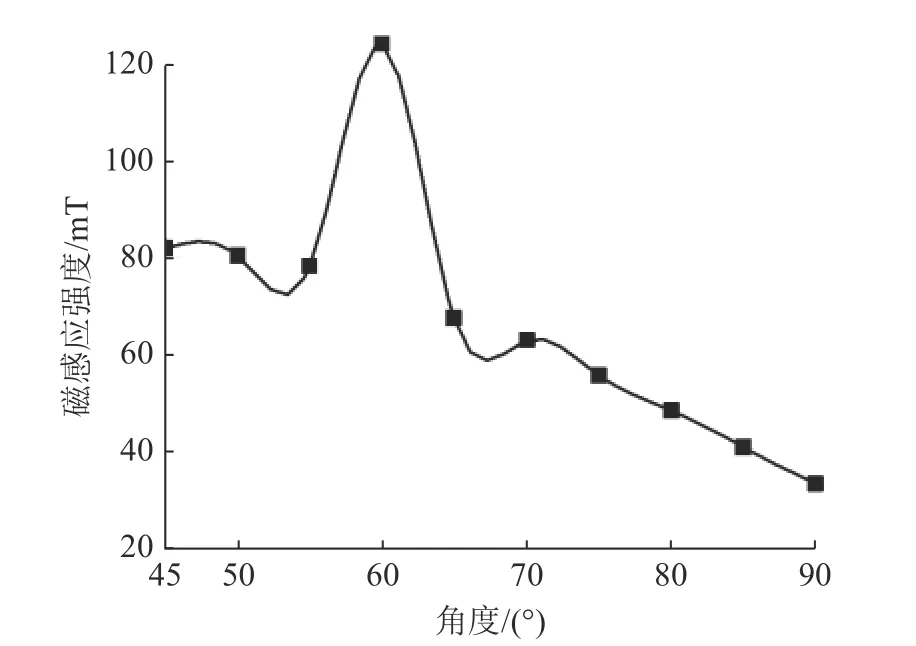
图3 导磁体腿部斜端面角度图Fig.3 Magnetic legs oblique surface angle diagram

由图3可见，不同导磁体腿部斜端面角度产生的磁感应强度变化具有一定规律，可以看出，斜端面角度为60°时磁感应强度值最大。因此，初步确定导磁体腿部角度为60°。

2.2 双径向永磁体旋向分析

由于系统中存在双径向永磁体，不同转向会对悬浮力产生影响，两种转向如图4所示。

图4（a）为双径向永磁体不同旋向状态，图4（b）为双径向永磁体相同旋向状态，转速均相同。为分析两种转向下永磁贴片的悬浮力，在仿真软件中设置导磁体斜端面与永磁贴片距离为6 mm，不同旋向与相同旋向的左、右、总悬浮力分别如图5、6所示。

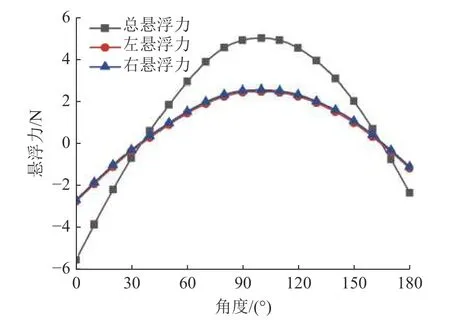
图5 不同旋向悬浮力Fig.5 Different rotational levitation forces

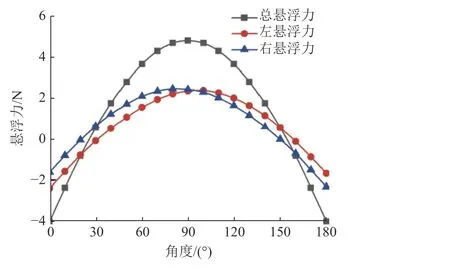
图6 相同旋向悬浮力Fig.6 Same rotational levitation force

对比图5、6可知：双径向永磁体不同旋向时，左、右两边永磁贴片悬浮力基本相同，但左、右、总悬浮力呈近似抛物线规律变化；当双径向永磁体相同旋向时，左、右两边永磁贴片悬浮力虽略有差距，但左、右、总悬浮力呈近似正弦规律变化，与径向永磁体圆周表面磁感应强度规律[17]基本相同。为了便于理论计算，选择系统中双径向永磁体为相同旋向。

2.3 系统运行原理

图7为在双径向永磁体相同旋向下，单点可控永磁支撑系统基于Maxwell仿真软件的2维分析结果。当径向永磁体处于初始0°时（图7（a）），左、右两边径向永磁体的磁力线从N极出发经由F型导磁体弧形部分和中间导磁体弧形部分回到左、右两边径向永磁体S极，无磁力线从斜端面出去，左、右两边永磁贴片无斥力，且硅钢具有铁磁性，永磁贴片对F型导磁体具有吸力，相当于S极。当左、右两边径向永磁体转动45°时（图7（b）），左、右两边径向永磁体的部分磁力线从N极出发经过F型导磁体及部分斜端面和中间导磁体回到左、右两边径向永磁体S极，则F型导磁体斜端面（表现出N极）与永磁贴片N极相对应，同性磁极相斥，使得永磁贴片悬浮，并且左、右两边产生的斥力分量在水平方向得以抵消，但永磁贴片悬浮力没有达到最大。当左、右两边径向永磁体转动为90°时（图7（c）），左、右两边径向永磁体磁力线从N极出发经过F型导磁体斜端面与中间导磁体回到径向永磁体S极，磁力线形成“蝶形”回路，此时，左、右两边永磁贴片斥力达到最大。

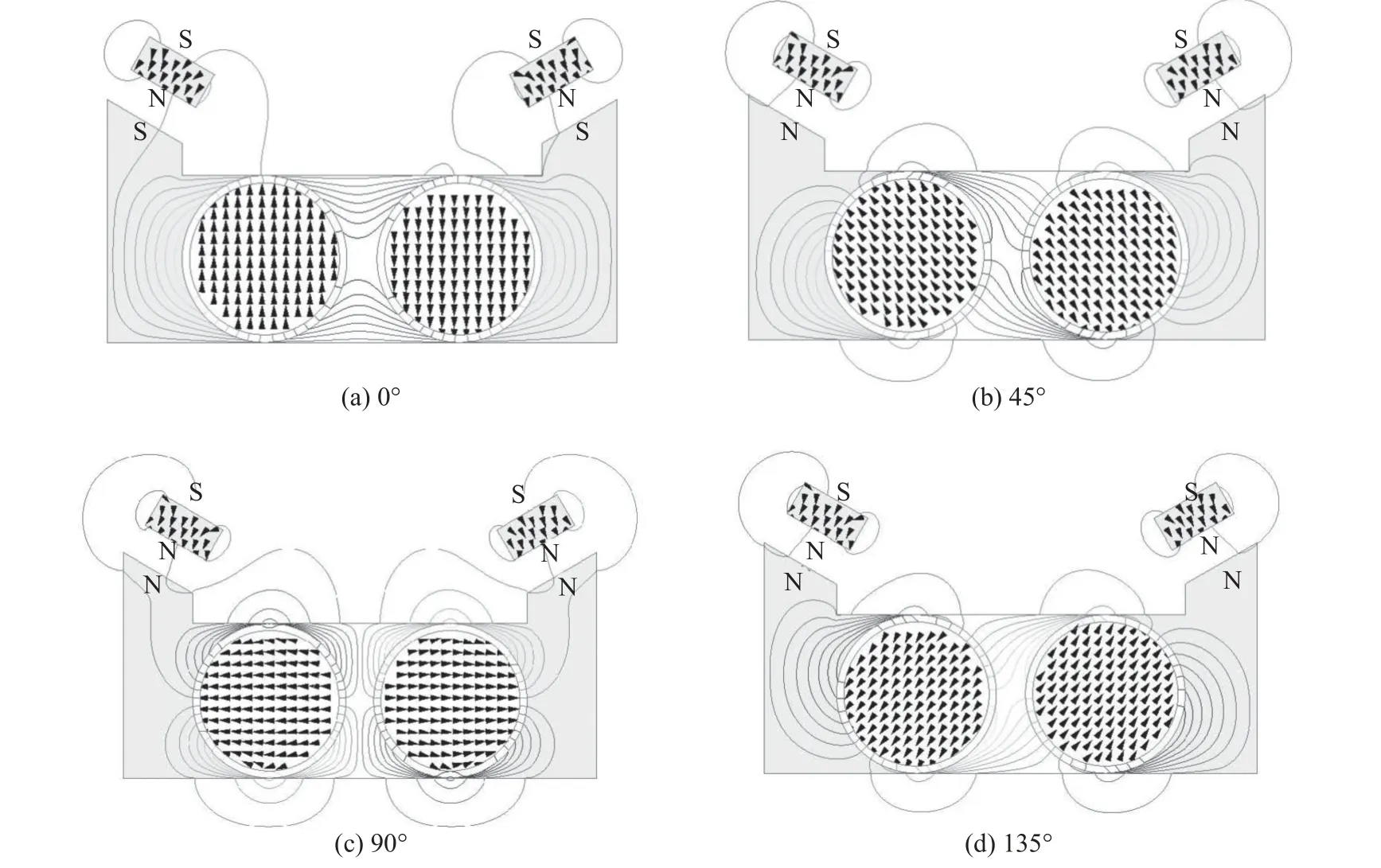
图7 单点可控永磁支撑系统有限元分析Fig.7 Finite element analysis of single-point controllable permanent magnet support system

转动角度继续增大，悬浮力开始减小。当左、右两边径向永磁体转动角度为135°时（图7（d）），部分磁力线从左、右两边径向永磁体N极出发经过F型导磁体及部分斜端面和中间导磁体回到S极，左、右两边永磁贴片斥力减小。当左、右两边径向永磁体转动180°时，磁力线经由F型导磁体弧形部分和中间导磁体弧形部回到径向永磁体S极，两边永磁贴片无斥力。

通过仿真实验分析可知：双径向永磁体在相同旋向且转速相同的情况下，左、右两边永磁贴片的悬浮力呈规律性变化。因此，可以实现调控单点可控永磁支撑系统的悬浮气隙。

3 单点系统悬浮力数学模型

3.1 数学模型建立

3.1.1 单点系统模型

基于磁导法求解单点可控永磁支撑系统模型的磁路和磁场，并作以下假设：

1）磁力线简化为直线和圆弧线，忽略磁路饱和。

2）忽略单点可控永磁支撑系统中良导磁材料（导磁体）及永磁体磁阻[17]。

3）忽略导磁体、永磁体端部漏磁。

其中，单点可控永磁支撑系统模型尺寸标注如图8所示，尺寸定义见表1。

表1 尺寸定义Tab.1 Dimension definition

图8 单点系统模型尺寸图Fig.8 Single point system model dimension drawing

将径向永磁体与导磁体等效为磁势变化的单点可控永磁支撑系统，分析系统中磁路的气隙磁导与漏磁导[17-18]，得出导磁体腿部的磁通量解析式，利用等效磁荷法求解永磁贴片表面磁场，结合永磁体间作用关系建立悬浮力数学模型，根据仿真实验确定相关系数。

3.1.2 导磁体腿部磁通量解析式

单点系统中双径向永磁体旋转使得整个磁路的磁通量和磁势不断变化，为了便于计算，将径向永磁体等效为磁势变化的长方体永磁体，等效后系统如图9所示。

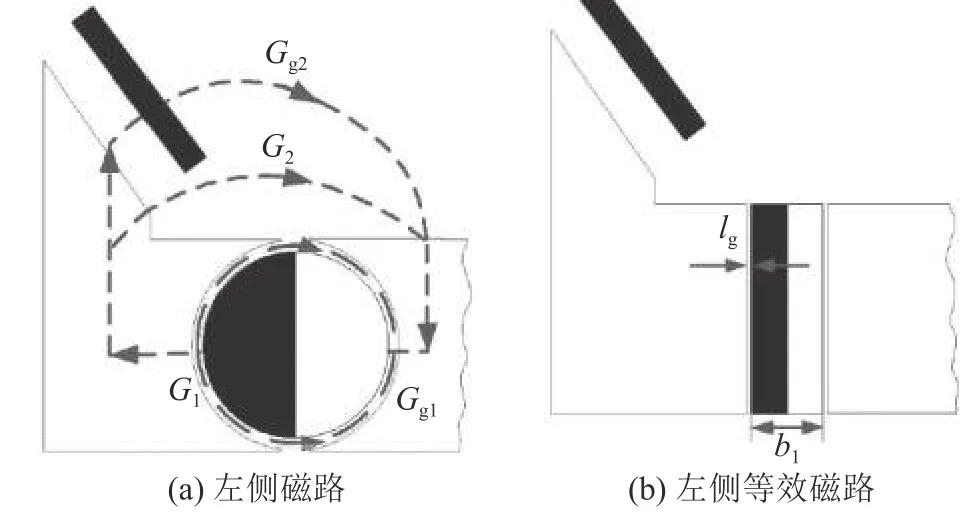
图9 系统等效磁路图Fig.9 System equivalent magnetic circuit diagram

图9中，Gg1为左边系统中导磁体与径向永磁体间的弧形气隙磁导，Gg2为左边系统中导磁体腿部斜端面与中间导磁体上端面的气隙磁导，G1为径向永磁体弧形气隙漏磁导，G2为导磁体腿部的斜端面下方的漏磁导，b1为等效后永磁体的宽度。

由于等效后永磁体工作面积S不变，又因为永磁体磁能与自身体积成正比，在磁能不变的情况下，等效后永磁体宽度b1为：

式中，V为径向永磁体体积。

由于径向永磁体圆周表面的磁感应强度近似呈正弦规律变化，因此，磁势也近似呈正弦规律变化，则左边系统磁势U为：

式中：Um为左边等效磁路中最大的磁势值，Um=Hhf，其中，H为磁场强度（与径向永磁体材料有关），hf为径向永磁体磁路长度。

考虑到各气隙处的漏磁，根据磁路欧姆定律确定左边系统的有效磁通Ф1为：

式中，σ1为左边系统中导磁体与径向永磁体间的弧形气隙漏磁系数，σ2为左边系统中导磁体腿部斜端面与中间导磁体的上端面漏磁系数。

通常，σ1、σ2的值与左边系统中磁路各部分结构的漏磁导及气隙磁导有关，其表达式为：

根据系统等效模型，左边径向永磁体与导磁体间的弧形气隙磁导Gg1表达式为：

左边导磁体腿部斜端面下方的漏磁导G2表达式为：

因此，左边系统导磁体腿部磁感应强度B1为：

式中：A为单个导磁体与永磁贴片对应的面积；k为系统固定悬浮系数，当系统结构不变时为常量。

3.1.3 永磁贴片表面磁场

采用等效磁荷法[19]的解析法[20-21]计算矩形永磁体作用面上的磁感应强度B2，其表达式为：

式中，Br为矩形永磁体剩磁，a2、b2为永磁贴片作用面下的矩形永磁体长、宽一半，h1为高度，d为计算位置到矩形永磁体作用面中心的垂直距离。

3.1.4 悬浮力数学模型

两个相同钕铁硼磁铁之间斥力[22-23]Fc为：

式中，ε为气隙修正系数，Mg为磁感应强度，Ag为永磁体磁极面积，h为钕铁硼磁铁之间距离。

径向永磁体与永磁贴片在气隙处磁感应强度B3为：

当角度在0°～180°之间时，左边导磁体腿部斜端面与永磁贴片间作用力简化为两块钕铁硼永磁体间作用力[24]，则系统悬浮力Ff为：

式中：Ff为系统导磁体腿部斜端面与永磁贴片间斥力；z为气隙在竖直方向分量；λ为近似常量，0＜λ＜1；λ1为修正系数。

将式（15）～（17）代入（14）整理得出：

3.1.5 确定修正系数

在Maxwell仿真软件中设置具体结构参数，参数值见表2。根据表2中系统结构参数，分别计算参数Gg1、σ1、Gg2、σ2、G1、G2。由于系统悬浮力模型中的修正系数λ1与气隙修正系数ε未知，因此通过仿真实验确定其数值。当永磁贴片与导磁体斜端面距离z1为6 mm时为相对零点z0，为确定λ1系数，在相对零点处将不同理论计算值λ1与仿真值进行对比，结果如图10所示；为确定气隙修正系数ε，固定径向永磁体角度为90°，将不同理论计算值ε与仿真值进行对比，结果如图11所示。

表2 系统结构参数Tab.2 System structure parameters

图10 确定λ1系数Fig.10 Determine λ1 coefficient

由图10可知，在相对零点处，随着角度不断增大，悬浮力先增大后减小，当修正系数λ1为12时，理论计算值与仿真值基本吻合[25]，因此确定修正系数λ1为12；由图11可知，随着气隙不断增大，悬浮力逐渐减小，呈非线性变化，在气隙为0～10 mm的状态下，气隙修正系数ε为200时与仿真值较为趋近，且下降速率基本相同，因此，确定气隙修正系数ε为200。

3.2 实验验证悬浮力模型

单点可控永磁支撑系统的实验装置如图12所示，主要包括径向永磁体、导磁体、永磁贴片、滑轨、标尺、滑块（图12中未标出）、USB-1608FS-Plus型数据采集卡、MIK-LCS1型拉压传感器（量程为0～5 kg，精度为0.000 3 kg）、NNA-WY100N激光位移传感器（精度为0.1 mm）、稳压电源模块、Arduino控制板、HBS57伺服电机驱动器、直流开关电源、60HSE4N-D25伺服电机、齿轮机构、电脑。

利用单点可控永磁支撑系统实验装置以相对零点为系统平衡点，获取平衡点处悬浮力与角度关系，悬浮力与角度的实验值与计算值对比如图13所示；固定双径向永磁体旋转角度为90°，得到悬浮力与气隙关系，图14对比了对于实验值与计算值，悬浮力与气隙的关系。

图13 悬浮力与角度关系对比Fig.13 Comparison of the relationship between suspension force and angle

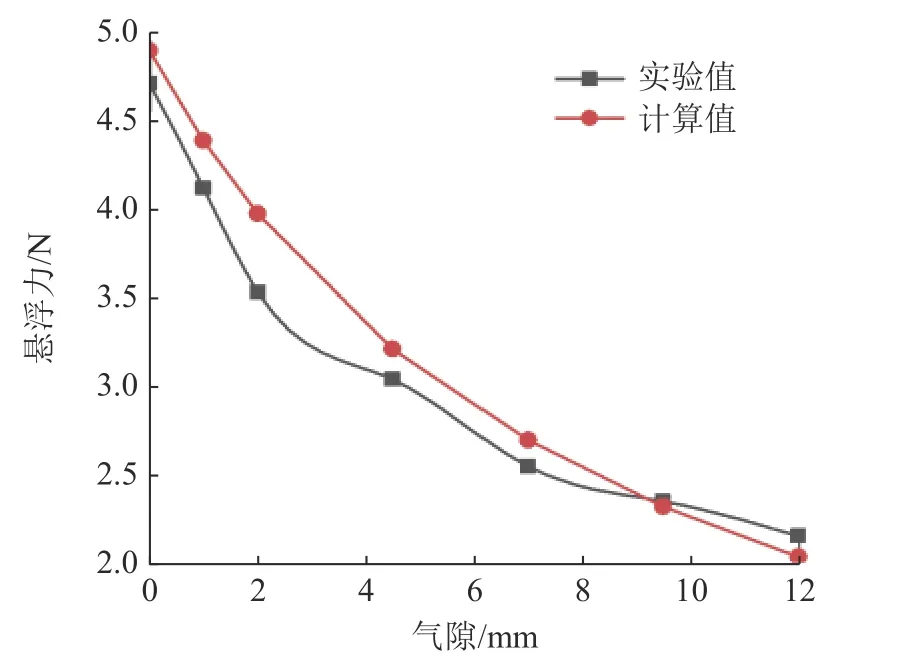
图14 悬浮力与气隙关系对比Fig.14 Comparison of suspension force and air gap relationship

如图13所示，在相对零点处悬浮力随着双径向永磁体旋转角度的增大呈现先增大后减小趋势，近似为正弦变化规律，其中，计算值与实验值略有差距，这可能是由于径向永磁体制作及充磁不均匀造成在轴向上磁场有所不同；如图14所示，固定旋转角度90°，悬浮力随气隙增大而减小，呈非线性变化，并且计算值与实验值基本相同，通过实验验证了理论计算模型的可靠性与准确性。

4 单点系统控制

4.1 单点系统动力学模型

根据单点可控永磁支撑系统结构及力学特性，得出系统的动力学微分方程：

式中，m为永磁贴片及组件质量，c1为空气的阻尼系数，g为重力加速度， Δz˙为悬浮物偏移相对零点z0的速度， Δz¨为悬浮物偏移相对零点z0的加速度。

由于式（21）中的悬浮力Ff为非线性力，并且只需考虑角度0°～180°的悬浮力，因此，需要在系统处于平衡位置附近进行线性化处理。

假设系统处于平衡状态时的位置为(z01，θ0)，则系统在悬浮平衡位置附近的悬浮力Ff可表示为：

式中，θ0为悬浮物在相对零点处的双径向永磁体转动角度， Δθ为悬浮物偏离相对零点位置转动的角度，z01为相对零点z0的距离， Δz为悬浮物相对于z0的距离。

在平衡位置(z01，θ0)对悬浮力Ff进行泰勒展开，并略去高阶无穷小量，则

由式（21）、（23）可得系统在平衡点附近的线性微分方程：

为判定单点可控永磁支撑系统的可控性和可观测性，根据平衡点附近的线性微分方程可建立系统的状态空间方程：

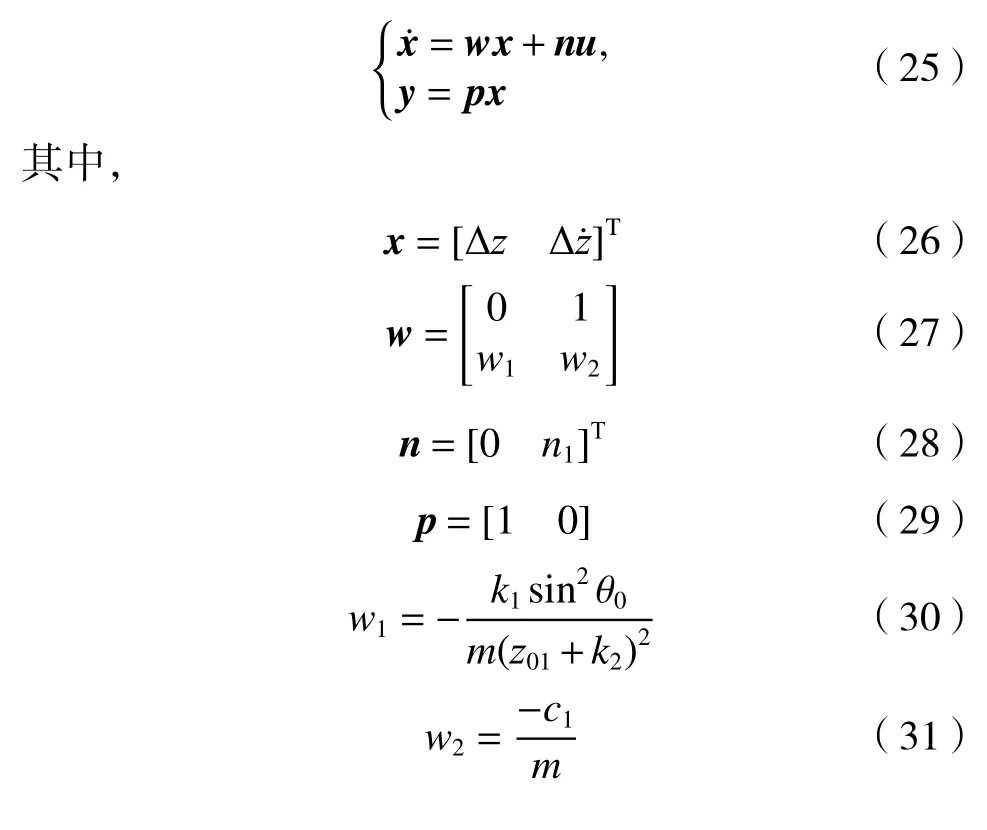
由式（35）、（36）可知，可控性和可观测性行列式值不等于零，因此，两矩阵均是满秩。由此得出结论：单点可控永磁支撑系统是完全可控和可观测的，从理论上验证了系统稳定悬浮的可行性。

4.2 电机控制系统

为了更好地设计电机控制系统，采用两相混合式电机（60HSE4N-D25伺服电机），该电机具有步距小、功耗低、频率范围宽、扭矩大等优点。对两相混合式电机进行简化分析，忽略定子极间漏磁、转子永磁体漏磁、轴向和径向磁阻，建立磁网格模型，如图15所示。

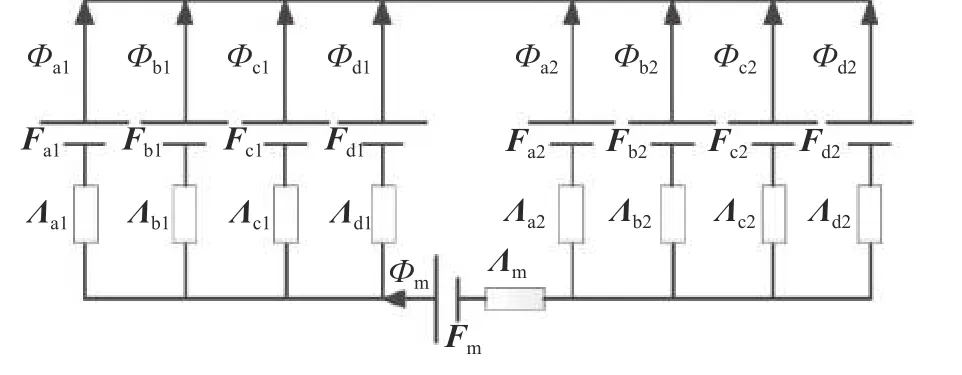
图15 磁网格模型Fig.15 Magnetic grid model

图15中，Λm为永磁体磁导，Fm为永磁体磁动势，Фm为永磁体磁通，Фa1、Фb1、Фc1、Фd1为N极转子铁心对应各极的磁通，Фa2、Фb2、Фc2、Фd2为S极转子铁心对应各极的磁通，Λa1、Λb1、Λc1、Λd1为N极转子铁心对应各极的齿间磁导，Λa2、Λb2、Λc2、Λd2为S极转子铁心对应各极的齿间磁导，Fa1、Fb1、Fc1、Fd1为N极定子绕组励磁磁动势，Fa2、Fb2、Fc2、Fd2为S极定子绕组励磁磁动势。

电机结构参数计算[26]如下：

式（37）～（40）中，L0为自感平均分量，E为定子绕组匝数，Λ0为定转子某相两个极的齿间磁导平均分量，Λ1为定转子某相两个极的基波分量，k0为自感分量系数，Nm为永磁体等效绕组匝数，L2为自感基波分量，Msr为系统互感常量，km为自感系数。

对于两相混合式电机的数学模型[26]如下：

式（41）～（42）中，uA、uB分别为两相绕组相电压，rA、rB分别为两相绕组的相电阻，iA、iB分别为A、B相电流，ψ为转子齿中心线与参考标的夹角，ke为反电动势系数，ωr为转子机械角速度，Te为电磁转矩，Nr为转子齿数，Im为转子电流，J为转动惯量，ν为摩擦阻尼系数，TL为负载转矩。

对于电机的等角度细分控制，一般电流公式[27]如下：

式中，ρ为电流实时角度，Nb为细分数，Sm为步数。

4.3 系统控制方法

为验证系统的悬浮可行性和系统响应特性，利用比例积分微分（PID）控制算法进行系统控制。PID控制器[28-29]是一种应用最为广泛的自动控制器，它具有原理简单、易于实现、适用面广、控制参数相互独立、参数选定比较简单等优点，PID控制的实质就是根据输入的偏差值，按照比例、积分、微分的函数关系进行运算，运算结果用以控制输出，连续控制系统的理想PID控制规律为：

式中，c(t)为系统输出，e(t)系统误差，Kp为比列系数，Ki为积分系数，Kd为微分系数，t为时间。

PID控制器是将偏差的比例P，积分I，微分D通过线性组合构成控制量，r(t)为系统输入，对被控对象进行控制，故称为PID控制器，本系统的PID控制系统原理图如图16所示。

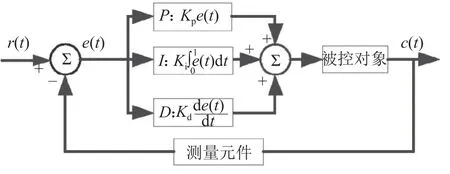
图16 PID控制原理图Fig.16 PID control schematic diagram

系统中被控对象为双径向永磁体，测量元件为激光位移传感器。

4.4 实验控制与仿真

控制系统的PID参数Kp、Ki、Kd分别取220.5、1 526.7、6.9，悬浮气隙设为12 mm，对单点可控永磁支撑系统进行PID控制研究与分析，气隙与时间关系的仿真与实验结果对比如图17所示，气隙与角度的仿真与实验结果对比如图18所示。

图17 气隙与时间关系对比Fig.17 Comparison of Air Gap and Time Relationship

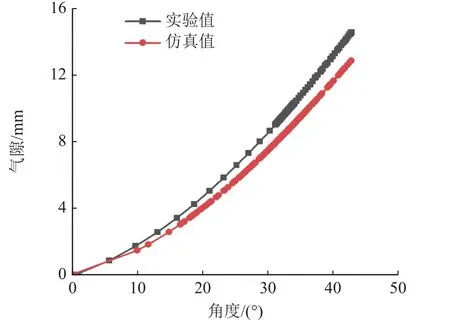
图18 气隙与角度关系对比Fig.18 Comparison of air gap and angle relationship

如图17所示，在仿真与实验中，系统经过PID算法控制均能稳定于气隙12 mm处，系统响应时间均小于0.9 s，仿真、实验均满足可控需求。

如图18所示，气隙随着径向永磁体转动角度的增大而增大，且由于径向永磁体充磁的不均匀使得气隙的实验值略大于仿真值。

5 结 论

1）综合考虑带式输送机托辊轴承中旋转阻力等问题，提出一种可控永磁支撑系统，采用FEM方法对单点可控永磁支撑系统的结构进行优化分析。分析确定导磁体腿部斜端面角度参数为60°，双径向永磁体采用相同旋向，这为可控永磁支撑系统结构布置方式提供一定参考。

2）通过磁路法建立单点可控永磁支撑系统中导磁体腿部磁通量模型，利用等效磁荷法确定永磁贴片表面磁感应强度，结合永磁体间作用力建立单点系统悬浮力数学模型，利用仿真实验确定修正系数λ1和气隙修正系数ε分别为12和200，并搭建单点实验平台，验证了理论计算模型的可靠性与准确性。

3）开展系统PID控制研究，仿真与实验结果表明，系统均能稳定于气隙12 mm处，响应时间均小于0.9 s，为低阻力带式输送机研究提供一定的理论与实验基础。