基于柔性边界的非饱和接触模型参数标定方法

张 杰，聂如松,2*，黄茂桐，谭永长，肖 玲

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 重载铁路工程结构教育部重点实验室，湖南 长沙 410075)

非饱和土在自然界广泛存在[1]，由固相（颗粒）、液相（水）和气相（空气）3部分组成，其特性研究在实际工程中应用前景广泛。非饱和土粒间吸力的存在使其力学行为（强度和变形）比饱和土或干土更为复杂。针对于此，研究人员采用各种试验方法对非饱和土的性质进行研究，如三轴试验[2-4]、直剪试验[5]。其中，三轴试验最为常见，三轴试验具有明确的应力路径、可控的排水条件及非人为限定的破坏面[6]。然而，室内三轴试验成本高、制样复杂、技术要求高，很难从细观尺度对试样的变形破坏进行深入分析。基于此，数值模拟被引进对三轴试验进行模拟，如离散元（DEM）和有限元（FEM）。但是，作为连续介质方法的FEM很难评估单个颗粒对材料力学行为的影响[7]，DEM比FEM可以更好的捕捉颗粒材料的力学行为，因此，近年来DEM使用更为广泛。

非饱和土的DEM研究中，多数学者采用线性平行黏结模型或线性接触黏结模型模拟土中的粒间吸力[7-9]，然而，这两种模型本身不符合非饱和土中粒间吸力的作用机制，使得应变软化现象加剧[10]。Jiang等[11]提出2维情况下考虑毛细作用的接触模型，Shen等[12]将其扩展到3维，该模型通过Young-Laplace公式计算基质吸力，可以反映粒间吸力的不均匀分布，然而该模型假设粒间吸力仅存在于接触颗粒间，与实际情况存在出入，并且由于基质吸力大小会受围压影响，导致该模型无法模拟不同应力状态下的试样[9]。最近，在离散元软件（PFC）中，Garnica等[13]开发了一种新的非饱和接触模型，称为Hill接触模型，该模型将吸力作为细观参数，克服了上述局限，与实际非饱和土粒间作用机制更为接近。

在DEM数值模拟中，颗粒和接触模型代表模拟材料的本构关系，因此模拟精度取决于模型细观参数的取值。一般来说，通过不断调整细观参数，可以获得所需的宏观力学指标。但这一过程很大程度上存在盲目性，导致时间消耗大、效率低。针对这一问题，有学者尝试改进参数标定的方法。Zhang等[14]模拟了堆石料的三轴试验，采用基于Box-Behnken设计（BBD）的响应面法对线性抗转动模型的细观参数进行标定。周喻等[15]基于BP神经网络对平行黏结模型的宏-细观参数进行匹配，但是，BP神经网络需要大量的随机组合样本才能具有较高的精度。徐国元等[16]采用迭代法对砂土三轴试验的宏-细观参数进行了标定。王晋伟等[17-18]采用正交-等值线法对堆石料的细观参数进行标定。杨文剑等[19]对碎石类材料细观参数进行了系统标定，揭示了碎石颗粒材料宏观力学参数与颗粒间细观参数的相关性，提出碎石颗粒材料数值模拟细观参数的标定方法。张权等[20]采用中心组合设计的方法对岩石材料宏-细观参数的相关性进行研究，标定其细观参数。刘相如等[21]采用正交试验设计不同组合的细观参数，通过多因素方差分析和回归分析研究了平直节理接触模型细观参数和宏观参数之间的关系。然而，以上参数标定方法大多用于岩石或非黏性土。目前，对于新的非饱和接触模型（Hill接触模型）的参数敏感性分析与系统标定未见报道，因此，需要对该接触模型细观参数进行系统标定，探究其宏-细观参数之间的关系。同时，DEM中边界条件是影响模拟精度的另一关键因素，在非饱和土DEM研究中，以往研究者基本都使用刚性墙作为侧向边界，刚性边界会抑制应变局部化（剪切带）的产生[22]，为了改善刚性边界的不足，采用一种类似于橡胶膜的柔性边界作为侧向边界。

以往研究中，鲜有人将柔性边界与试验设计方法结合起来应用于非饱和接触模型的参数标定，本文首次将这两种方法结合起来，建立柔性边界下非饱和接触模型细观参数标定流程。通过正交试验设计对细观参数的取值范围进行优化，采用基于中心复合试验设计（CCD）的响应面分析方法建立非饱和土宏-细观参数的关系式；基于此关系式，建立非饱和土细观参数的最优化模型，并使用MATLAB中的FMINCON函数对其进行求解，获得具体的细观参数。在此基础上，模拟不同围压下非饱和土的三轴试验并与试验结果进行对比，验证所标定参数的有效性，为进一步分析非饱和土的细观力学性质提供基础。

1 非饱和土三轴试验模拟原理及参数标定流程

1.1 非饱和接触模型

非饱和土粒间存在毛细作用力，毛细作用力作为短程作用力，随粒间距离增加而减小，直至消失。因此，采用一种考虑毛细作用力的非饱和接触模型，称为Hill接触模型[13]。非饱和接触模型如图1所示，该接触模型在赫兹接触模型的接触上加入了毛细作用力。图1（a）中，法向单元上的力学元件主要有弹簧、黏壶、吸引器、分离器，切向单元上的元件主要有弹簧、分离器、黏壶。

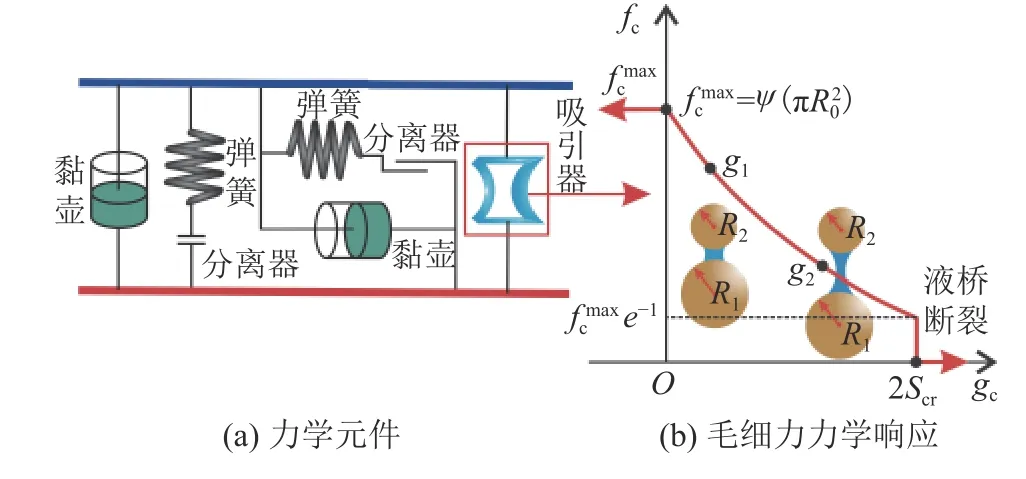
图1 非饱和接触模型示意图Fig.1 Unsaturated contact model considering intergranular suction

赫兹接触模型为基本模型[23]。毛细力fc通过式（1）计算：

式中：ψ为吸力；2Scr为毛细力的作用范围；gc为颗粒间距；R0=Scr= min(R1,R2)，其中，R1、R2为两颗粒半径。

图1（b）中，水分的存在使两颗粒之间建立液桥，产生毛细力。当颗粒接触时，液桥产生，此时毛细力最大；随粒间间距增大，毛细力呈指数衰减；分开至临界距离2Scr时，液桥消失，毛细力变为0。

1.2 围压柔性加载原理

在三轴试验模拟中，使用相互黏结的等粒径小颗粒组成柔性橡胶膜，颗粒呈六边形排列。膜颗粒之间采用线性接触黏结模型，保证颗粒间只传递力不传递力矩。当法向力或切向力超过拉伸强度时，膜颗粒间的黏结会破坏，为了防止柔性边界在大体积变形时破坏，将拉伸强度设定为一个极高值。柔性膜的参数参考了Zhang等[24]的研究成果，见表1。

表1 柔性膜的基本参数Tab.1 Basic parameters of flexible membrane

图2为柔性边界示意图。为防止试样颗粒从膜颗粒中穿出，应保证膜颗粒的尺寸足够小。考虑到颗粒数目对计算效率的影响，根据相关研究[7]，将膜颗粒半径设置为试样最小颗粒半径的1.5倍，此时既能保证运算效率，又能防止大变形时试样颗粒从膜颗粒中穿出。使用线性接触黏结模型将“O”形环粘在加载板上，使其与加载板同步运动，柔性膜具体构建方法见文献[25]。柔性膜构建方法并非首次提出，然而本文首次将其应用于DEM非饱和接触模型的标定。

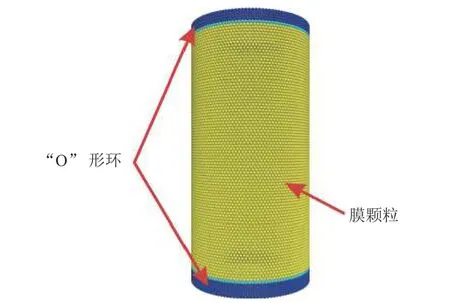
图2 柔性边界示意图Fig.2 Schematic diagram of flexible boundary

1.3 三轴DEM分析模型

试验材料为低液限粉土，取自朔黄铁路基床表层，通过配置含水率，使其处于非饱和状态，其基本物理参数见表2。试样为圆柱形，高度和底面直径分别为80.0 mm与39.1 mm；通过考虑真实基床表层填料所受围压状况，设置3个水平的围压，分别为30、60、90 kPa。

表2 非饱和土试样的基本物理参数Tab.2 Basic physical parameters of unsaturated soil

根据室内三轴试验，将数值试样设置直径为39.1 mm，高度为80.0 mm的圆柱体。因现有计算能力限制，无法生成真实试样的粒径级配曲线，但理论研究表明，只要选取尺度相关的微观本构，放大粒径试样与原粒径试样具有相同的力学响应，但应保证3维模拟单元试验颗粒数目大于40 000[26]，假设模拟的粒径级配曲线为线性，采用颗粒排斥法生成指定孔隙率的试样，最终颗粒数目为59 195，粒径级配曲线与最终生成模型如图3所示。

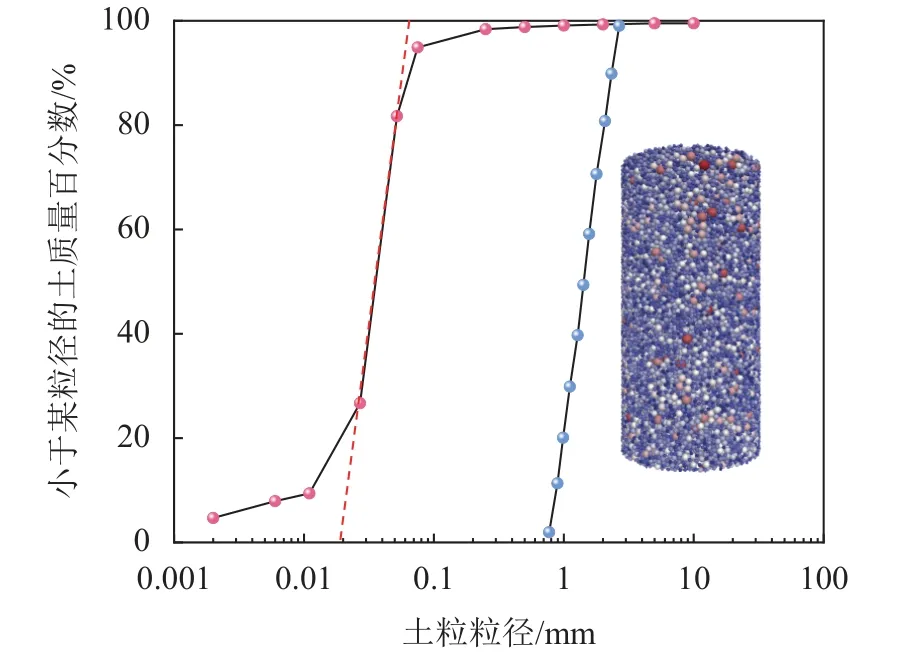
图3 室内测试和数值模拟的粒径级配曲线Fig.3 Particle size distribution curves in laboratory tests and simulations

柔性边界下三轴试验模拟步骤如图4所示。具体如下：1）在39.1 mm×80.0 mm（直径×高）的圆柱体内制备预定粒径及孔隙比的试样；2）对样品颗粒添加非饱和接触模型，在刚性边界条件下进行初始固结，通过伺服使其达到预定围压；3）生成柔性边界，删除原刚性侧壁边界，在柔性边界条件下进行二次固结，使其达到平衡状态，实现柔性等向固结；4）赋予上下加载板一个恒定速度，对试样进行加载，加载速度设置为0.01 m/s，当轴向应变达到16%时，结束加载，完成试样剪切。

图4 柔性边界下三轴模拟试验流程Fig.4 Flow of triaxial numerical test under flexible boundary

1.4 参数标定

在DEM中，通过定义颗粒间接触的细观参数,计算颗粒的运动和相互作用，从而实现对颗粒材料复杂力学问题的模拟和分析。因此，数值模拟可靠性取决于非饱和接触模型细观参数的准确标定。本文参数标定流程如图5所示，步骤如下：

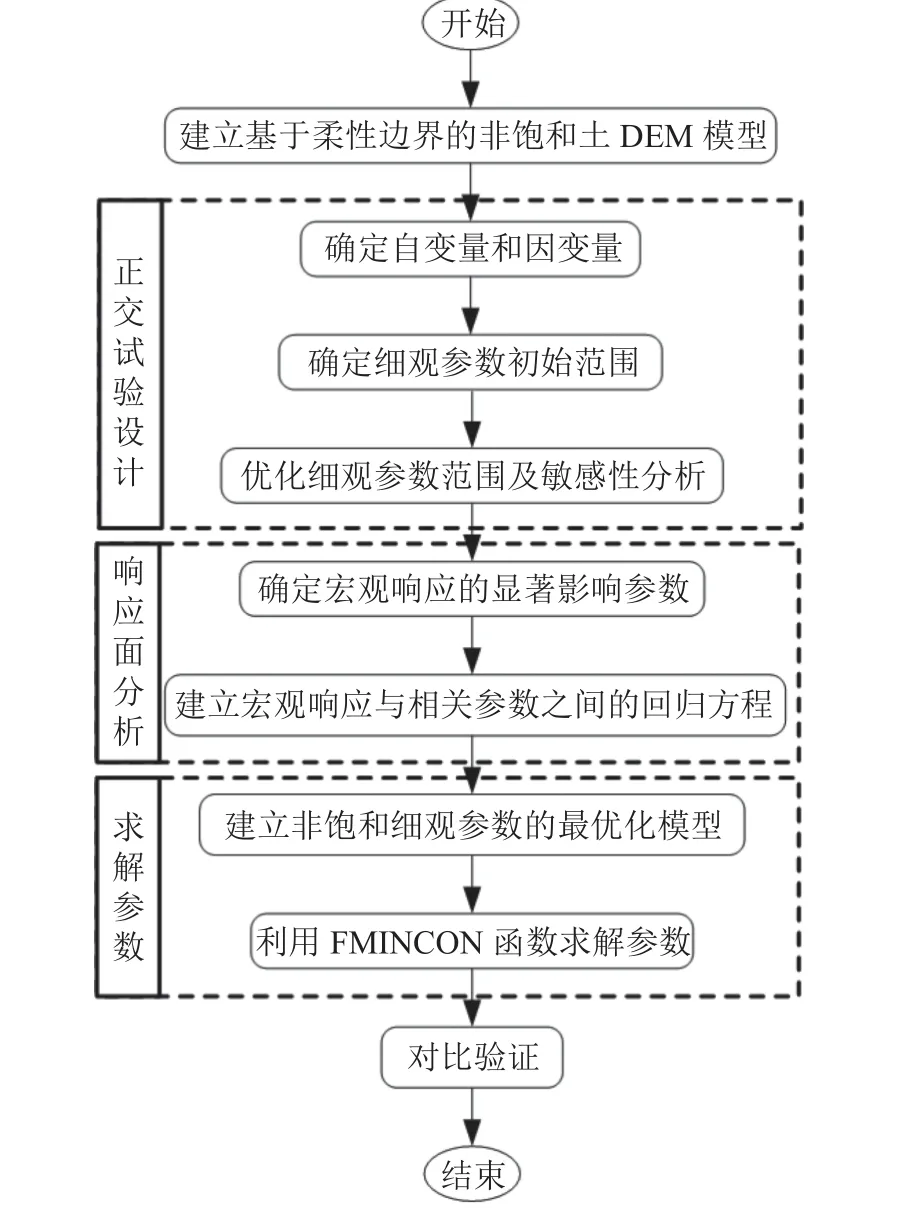
图5 非饱和接触模型参数标定流程Fig.5 Flow chart of parameter calibration of unsaturated contact model

1）通过室内试验测得非饱和土的颗粒级配曲线、孔隙率、密度，获得三轴试验数值模拟的基础参数，并建立基于柔性边界的非饱和土三轴DEM分析模型。

2）确定正交试验设计的自变量和因变量及细观参数的初始范围，通过多次正交试验设计优化细观参数的取值范围，并对参数敏感性进行分析。

3）确定对宏观响应影响显著的细观参数，在优化的细观参数取值范围内，使用基于中心复合试验设计（CCD）的响应面分析方法建立宏观参数与细观参数的回归方程。

4）建立细观参数的最优化模型，使用FMINCON函数求解最优化模型，获得细观参数的最优解。

5）使用最优参数进行不同围压下的三轴试验模拟，并与试验结果进行对比，验证标定结果的可靠性。

2 参数敏感性分析

在三轴试验模拟中，使用60 kPa围压的室内三轴试验结果来标定模拟中的细观参数。正交试验设计能从全面试验中挑选出代表性强的试验，具有代表性强、试验次数少的优点[27]。在标定参数前使用正交试验设计，优化细观参数的取值范围，减少后续参数标定的工作量。

2.1 自变量和因变量的确定

采用考虑粒间吸力的非饱和接触模型，接触模型的细观参数分别为摩擦系数µ、杨氏模量E、泊松比υ和吸力ψ。通过室内三轴试验的宏观特性与离散元模拟结果进行对比，标定细观参数。选取的宏观参数为割线模量E50、峰值强度Sp，宏观参数的定义如图6所示，其中，割线模量E50通过式（2）计算：

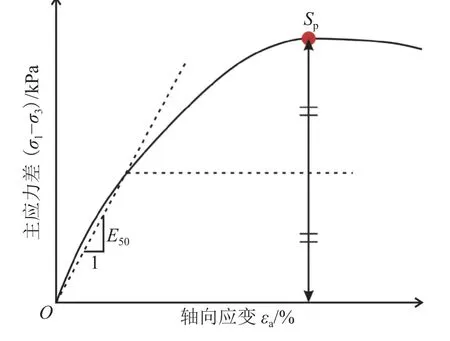
图6 宏观力学参数示意图Fig.6 Schematic diagram of macro-mechanical parameters

综上，正交试验设计中的自变量为(µ、E、υ、ψ)，因变量为(E50、Sp)。

2.2 细观参数初始范围的确定

细观参数初始范围确定原则：使用该范围细观参数确定的正交试验得出的模拟结果应包含室内试验结果[18]。表3为细观参数初始范围及相应的正交设计表，表4为模拟结果。

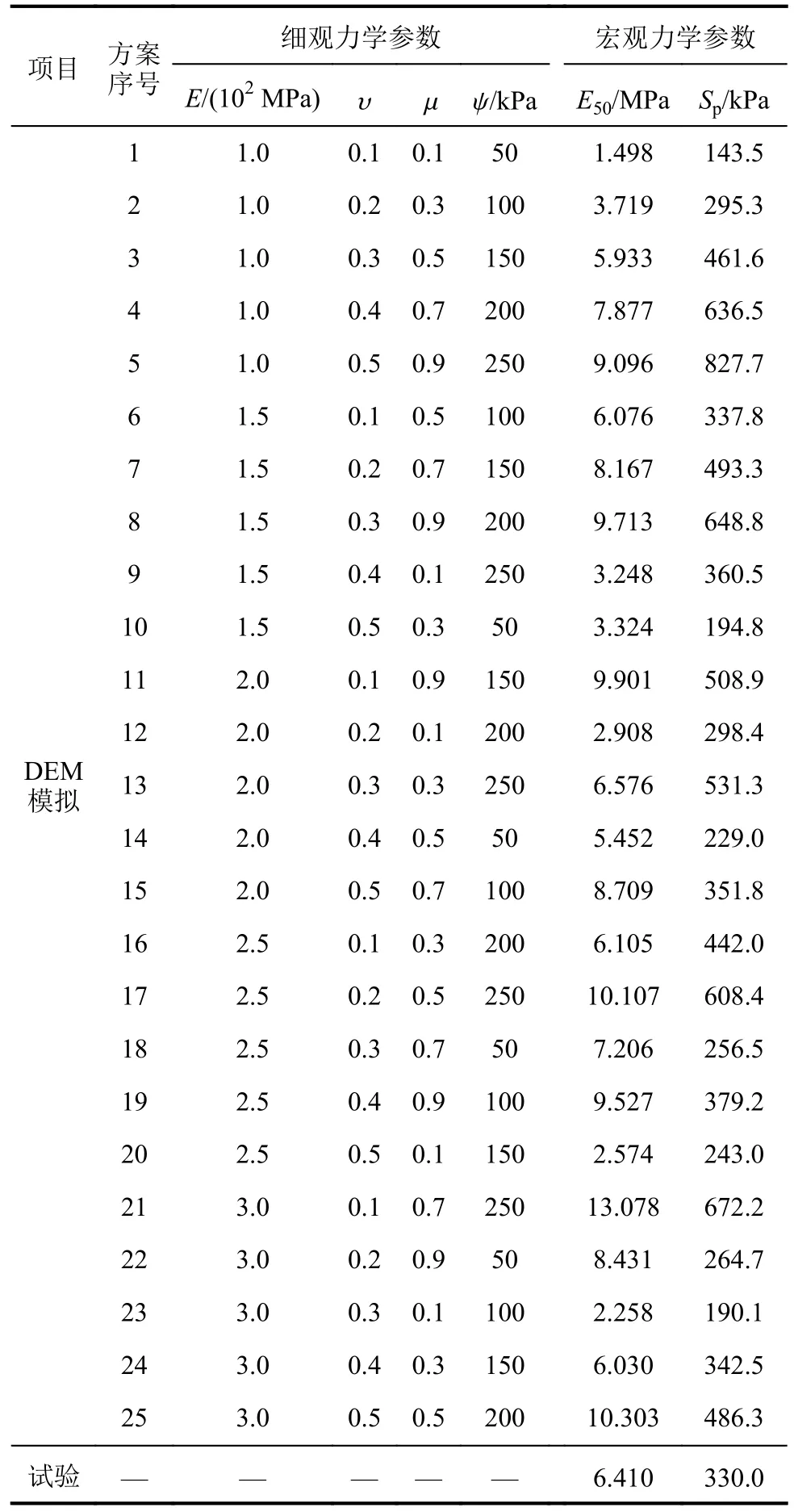
表4 第1次正交设计试验方案及结果Tab.4 Schemes of micro-parameters and results of macroscopic indexes in first orthogonal tests

2.3 细观参数范围的优化及敏感性分析

正交试验确定的最优方案是试验结果中满足目标的因变量对应的自变量的组合[28]。本文目标是两个宏观力学参数的离散元数值模拟值与室内试验值最接近。由表4可知：方案6中，Sp为337.8 kPa,与试验结果330.0 kPa最为接近；方案13中，E50为6.576 MPa，与试验结果6.410 MPa最为接近。因此，选取数值模拟方案6和13作为最优方案。根据最优方案，对细观参数的取值范围进行缩小，使各细观参数的取值范围包含在最优方案的范围内，进行二次正交试验，二次正交试验结果见表5。

表5 第2次正交设计试验方案及结果Tab.5 Schemes of micro-parameters and results of macroscopic indexes in second orthogonal tests

由表5可知，方案22是最优方案，第2次正交优化后各细观参数的取值范围较小。因此，不需要进行第3次正交设计。

采用极差分析法分析表5的检验数据[28]，以确定各细观参数的敏感性，结果见表6。表6中：ki为表5中不同因子水平i(i= 1、2、3、4、5)，即各细观参数值相同时宏观力学参数的平均值；R和Rr分别为宏观力学参数的范围和相对范围，其中，Rr代表细观参数的变化对宏观力学参数的影响程度，Rr越大，细观参数的变化对宏观力学参数的影响越大。R和Rr可通过式（3）进行计算：

表6 二次正交极差分析结果Tab.6 Analysis results of the second orthogonal test

式中，Ri为某一细观参数水平值变化对应的宏观指标范围。

细观参数的变化对宏观力学参数的影响如图7所示。图7（a）为细观参数对E50的影响，可以看出，µ和ψ对E50的影响最大，其次为E，υ对E50几乎无影响。图7（b）为细观参数对Sp的影响，可以看出，ψ对Sp的影响最大，其次为µ，E和υ对Sp影响较小。综上，在第2次正交试验参数选取范围内，各细观参数对宏观响应的影响程度排序如下：E50：µ＞ψ＞E＞υ；Sp：ψ＞µ＞E＞υ。

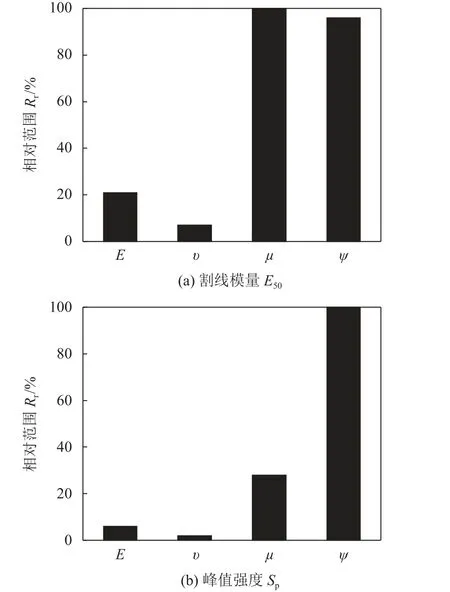
图7 宏观力学参数的敏感性分析结果Fig.7 Range analysis results of macroscopic mechanical parameters

3 细观参数确定及优化

3.1 响应面分析

根据敏感性分析，细观参数对宏观力学参数的影响程度不同。在把握主要因素，忽略次要因素的基础上，采用基于中心复合试验设计（CCD）的响应面法拟合因素与响应值之间的函数关系[29]。通过敏感性分析可知，对E50影响显著的细观参数为：µ、ψ和E；对Sp影响显著的细观参数为ψ和µ。因此，进行3因素5水平的CCD响应面分析。细观参数υ对E50及Sp的影响均较小，选取第2次正交设计中与试验结果最为接近的方案22中的υ作为参数，取值为0.15。利用Design Expert生成响应面分析结果，响应面分析结果见表7。值得注意的是，在CCD设计中，为了更好地拟合相应曲面，有一些点会超出原定的水平。

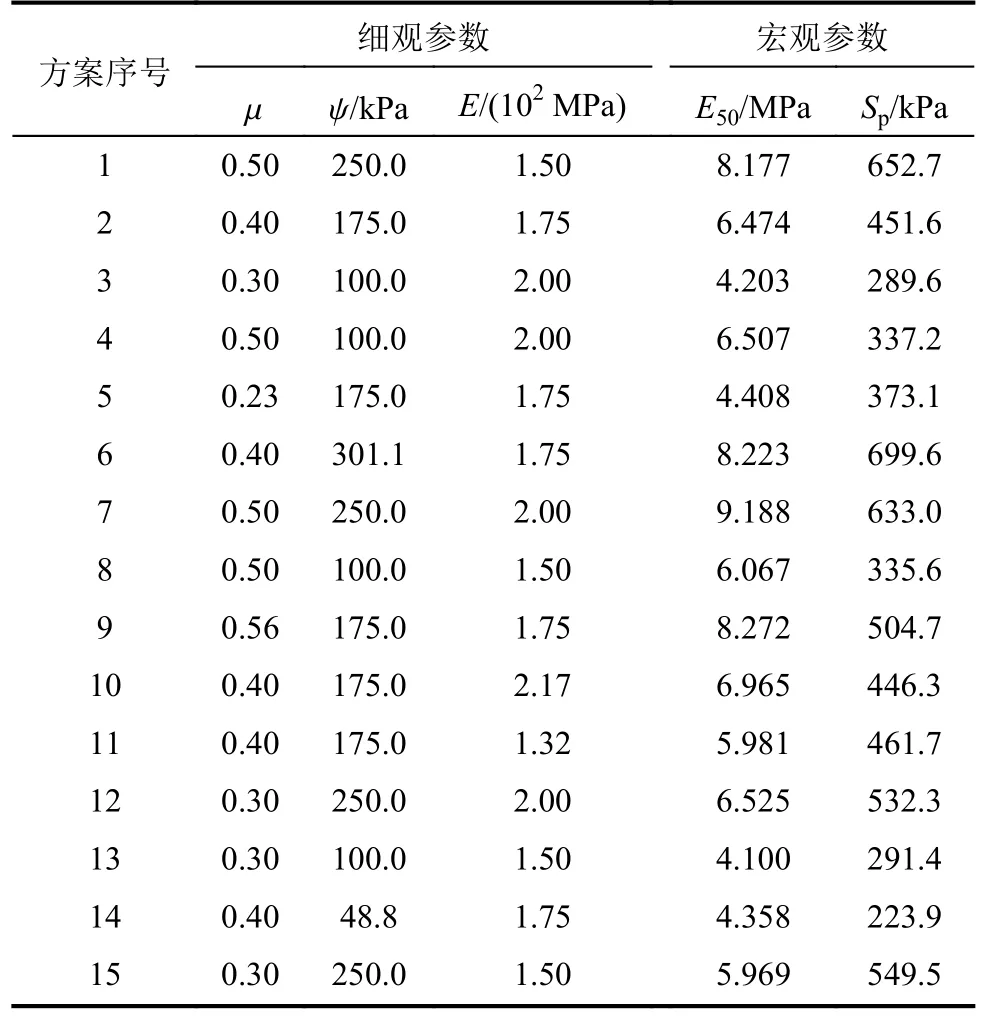
表7 响应面分析结果Tab.7 CCD matrix and test results

通过响应面分析得到回归方程如式（5）、（6）所示：

式中，y1、y2分别为E50和Sp的数值，x1、x2、x3分别为µ、ψ和E的数值。

E50和Sp的响应面如图8所示。由图8可以看出：E50的响应面在µ、ψ和E增大的方向上，高度也相应增大，即随µ、ψ和E的增大，E50也随之增大；但在µ、ψ方向上的斜率要明显大于E，表明响应值对µ、ψ更敏感；在Sp的响应面上，ψ方向的斜率明显大于µ和E，说明响应值对ψ的变化最敏感。响应面分析的结果与敏感性分析结果一致。

图8 割线模量E50和峰值强度Sp的响应面Fig.8 Response surface of E50 and Sp

3.2 细观参数优化

目标函数：

约束：

采用MATLAB优化算法工具箱中的FMINCON函数对有约束优化问题进行求解，标定所得最终参数及其他基本参数见表8。

表8 标定后的细观参数取值Tab.8 Material properties used in simulations

采用表8中的参数进行60 kPa柔性边界下的离散元三轴试验模拟。图9为离散元模拟结果与室内试验结果的比较。由图9可见，离散元模拟曲线与室内试验吻合良好，在离散元模拟中很好地预测了割线模量E50及峰值强度Sp。

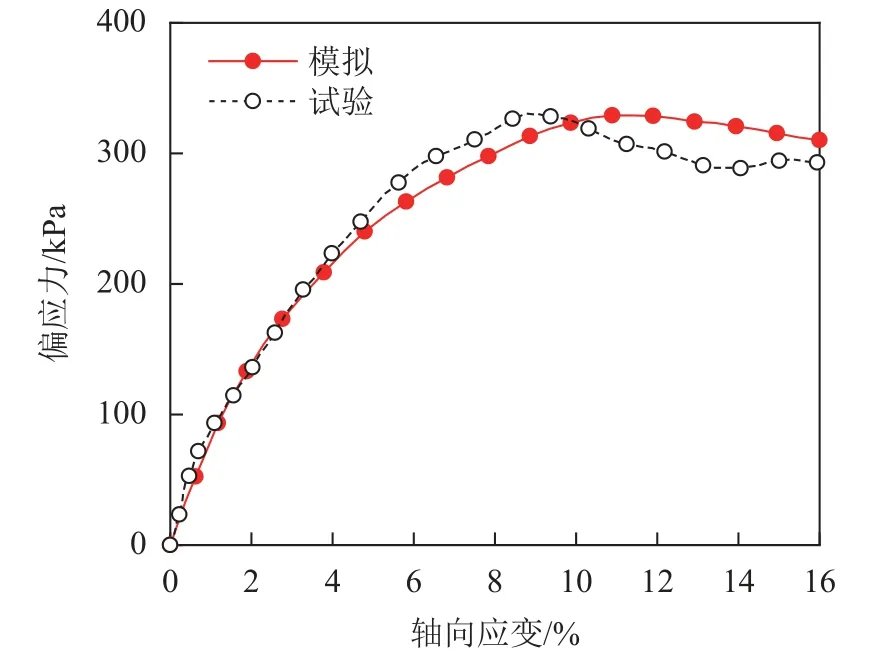
图9 60 kPa时模拟与试验应力应变曲线对比Fig.9 Deviatoric stress versus axial strain curves of the laboratory tests and DEM simulations under confining pressure of 60 kPa

三轴剪切完成后，试样的形态如图10所示。由图10可见，模拟试样表现为中部鼓胀，与室内试验较为一致，图10（c）中可以观察到剪切带。值得说明的是，本文参数标定方法仅针对非饱和接触模型，对于其他接触模型的适用性仍需进一步检验。

图10 60 kPa试验完成时模拟与试验试样形态对比Fig.10 Morphology of the laboratory tests and DEM simulations under confining pressure of 60 kPa

为了进一步验证标定结果，使用表8中的细观参数模拟室内三轴试验，围压分别为30、90 kPa，结果如图11所示。由图11可见，离散元模拟曲线与室内试验曲线在部分区域存在一定差异，但总体上呈现出一致的趋势，说明数值模拟能有效预测室内试验结果。

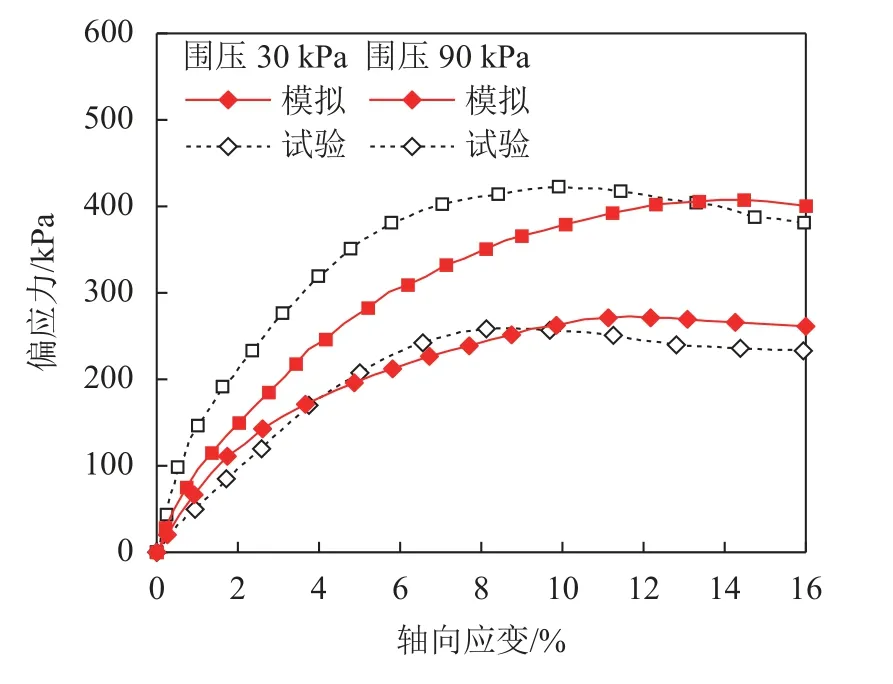
图11 30 kPa和90 kPa时模拟与试验结果对比Fig.11 Deviatoric stress versus axial strain curves of the laboratory tests and DEM simulations under confining pressures of 30 kPa, 90 kPa

图12为三轴DEM模拟与室内试验获得的抗剪强度包络线对比。由图12可见，两者十分接近，说明标定的参数能反映试样的力学性能。

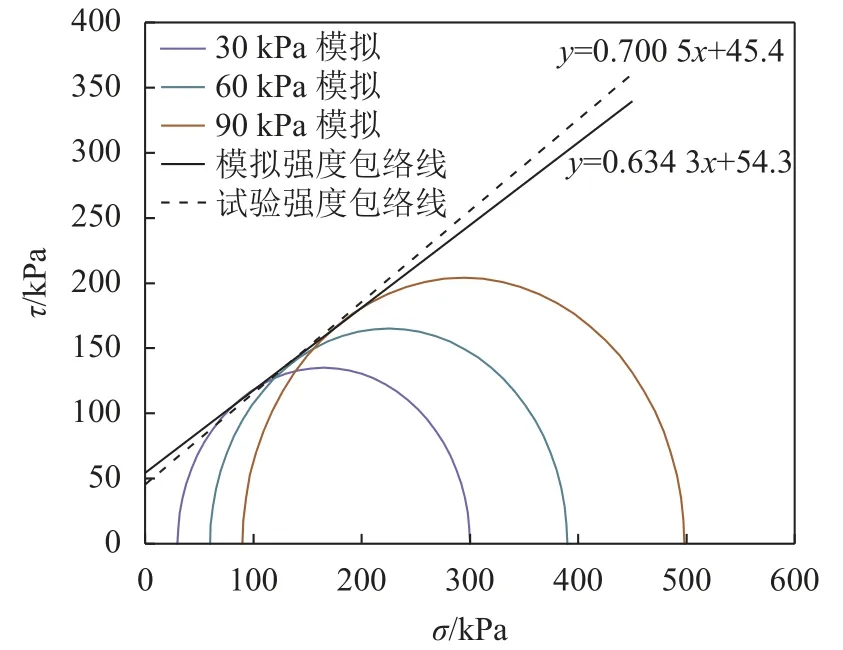
图12 试验和DEM模拟强度包络线对比Fig.12 Comparison of strength between triaxial simulations and laboratory tests

4 结 论

本文将正交试验、响应面分析与优化函数结合起来，提出基于柔性边界的非饱和接触模型参数标定方法，主要结论如下：

1）提出了基于柔性边界的非饱和土三轴试验参数标定流程，首先通过正交试验设计优化细观参数的取值范围，然后利用基于CCD的响应面分析方法建立非饱和土宏观响应与细观参数之间的非线性关系，最后建立非饱和土细观参数的最优化模型，使用FMINCON函数求解获得具体的细观参数。

2）非饱和接触模型细观参数的敏感性分析可知，在优化后细观参数范围内，各细观参数对不同宏观指标的影响程度不完全相同。割线模量E50主要受摩擦系数µ、吸力ψ、杨氏模量E影响，其影响程度为µ＞ψ＞E；峰值强度Sp主要受吸力ψ、摩擦系数µ影响，其影响程度为ψ＞µ＞E。

3）采用标定后的参数模拟不同围压下的三轴试验，获得抗剪强度包络线，并与室内试验结果进行对比，验证了标定结果的可靠性，说明标定的参数能反映试样的力学性能。