地铁高架桥列车振动荷载对邻近构筑物受力变形的影响

刘维正，王 锋，罗桂军，徐毅夫，唐新建

(1.中南大学 土木工程学院，湖南 长沙 410075；2.中南大学 高速铁路建造技术国家工程研究中心，湖南 长沙 410075；3.中建五局土木工程有限公司，湖南 长沙，410004)

随着中国城市轨道交通的快速发展，城市空间利用率不断提高，路网交会的情况越来越多，在部分线路节点上不可避免地出现一些新建桥与既有构筑物交叉或并行的现象[1]。桥梁桩基础的施工和列车运营振动荷载易使周围土体产生附加应力和位移[2]，若处理不当很有可能影响既有构筑物的安全，严重会导致其倾斜、开裂，甚至破坏，从而造成巨大的经济损失[3]。因此，为保证既有构筑物的正常使用，有必要针对运营期地铁高架桥列车振动对既有构筑物的影响进行研究，将既有构筑物受新桥运营所产生的影响控制在合理范围内。

目前，不少学者针对桩基对既有构筑物的影响进行了分析，主要研究方法有理论分析、数值模拟、现场实测和模型试验等。理论分析方面：项彦勇等[4]提出一种预测桩基荷载对隧道开挖塑性区形状和范围的理论方法，分析了桩基荷载的形式、大小和位置对隧道开挖塑性区的影响。Zou[5]使用量纲分析法，基于ABAQUS数值模拟，提出依据桩顶沉降计算隧道沉降的方法。数值模拟方面：路平等[6]运用拟静力法研究桩基础施工及加载运营期对既有隧道结构和轨道变形的影响，分析单个承台桩基础及多个承台桩基础对邻近既有隧道的影响规律。李杨秋[7]分析了群桩基础在不同加载工况下，隧道衬砌的内力和位移变化，并根据模拟结果确定了工程安全系数。方淑君等[8]采用静力加载，研究了新桥运营荷载作用下既有桥桩横桥向的附加水平变形。王景春等[9]以新建桥梁下穿高铁桥梁为背景，施加静力荷载，研究桩基施工与后期运营对群桩基础变形的影响。邢凯等[10]建立3维数值模型，分析桩体施工与承载运营过程中对隧道结构的影响。丁智等[11]建立桩-隧相互作用有限元模型，通过改变桩隧相对位置、隧道埋深、水平净距等因素，研究静压桩基施工对既有隧道的影响。吕宝伟[12]采用MIDAS建模，计算桥梁桩基施工对隧道结构内力和位移的影响。孙宗磊[13]对新建桥梁邻近既有高铁桥梁进行分析，确定了合理的并行线间距。Lueprasert等[14]研究了桩基承载对隧道结构影响，提出一种隧道变形评估方法。现场实测方面：丁智等[15]分析了桩基施工及后期沉降对邻近隧道的影响。 谢伟平等[16]对砖石古塔进行地脉动测试，结合数值模拟研究地铁列车荷载作用下塔体水平振动速度的变化规律。邱陈瑜等[17]基于现场实测，采用有限元强度折减法，对桩基荷载作用下隧道的破坏模式进行研究。Wang等[18]研究了移动荷载作用下桩基的振动特性。模型试验方面：安建永等[19]基于模型试验与数值模拟，分析了不同桩长和桩隧水平距离下桩基荷载对隧道支护内力的影响特征。杨文波等[20]采用模型试验与数值模拟相结合的方法，研究列车振动荷载作用下隧道及周围土体的动力响应特性。翁效林等[21]通过改进离心场桩基加载装置和试验监测设备进行离心试验，分析桩基础承载过程对邻近既有隧道的变形和受力影响。张玉伟等[22]开展不同桩端荷载、不同桩距比影响下承载桩基对近距隧道影响的离心模型试验，发现承载桩基对邻近隧道具有明显的附加荷载作用。

综上可见，高架桥对既有构筑物的影响分析多集中在桩施工与承载阶段，对运营阶段的研究主要针对的是高铁列车，对于地铁列车振动荷载对邻近敏感性构筑物影响的研究不多；少量的研究也是采用拟静力法，忽略了运营期是一个动态加载的过程。为此，本文以长沙地铁1号线北延线上跨石长铁路框架桥和绕城高速桥为背景，采用动力分析方法模拟地铁高架桥运营振动荷载下既有构筑物的动力响应特征，研究不同轴重、不同车速、不同近接距离、不同阻尼比和加固措施对动力响应的影响，为新建地铁高架桥运营期间紧邻桩基和框架桥的安全正常运营提供参考。

1 工程概况

1.1 工程背景

新建的长沙轨道交通1号线北延一期工程青竹湖路站至冯蔡路站区间采用高架桥形式沿芙蓉北路中央敷设。该区段芙蓉北路采用上跨既有绕城高速公路和石长铁路西北联络线、正线，形成综合立交体系。地铁高架桥采用55 m+85 m+49 m连续梁跨越芙蓉北路。其中，连续梁中跨85 m跨越绕城高速桥，边跨49 m跨越石长铁路西北联络线及正线。连续梁桥墩为矩形截面，主墩墩身尺寸为4.0 m×3.0 m，墩顶尺寸为5.5 m×3.0 m，高7.5 m，埋深2 m；承台尺寸为6.7 m×10.5 m×3.0 m，下设6根直径为1.8 m的钻孔灌注桩，桩中心距3.8 m，桩长68.0 m。过渡墩墩身尺寸为3.0 m×2.5 m，承台尺寸为6.5 m×6.5 m×2.2 m，下设4根直径为1.5 m的钻孔灌注桩，桩中心距3.8 m，桩长66.0 m。存在邻近施工影响的既有构筑物由北往南分别为跨绕城高速桥台、8.0 m框架桥、15.5 m框架桥。新建桥梁与既有构筑物的剖面图与平面图与如图1、2所示。图1、2中，19#桥墩承台边缘一侧距离跨绕城高速桥台最小距离约为0.94 m，另一侧距离石长铁路框架桥最小距离为1.53 m。

图1 新建桥梁与既有构筑物剖面图Fig.1 Sectional view of new bridges and existing structures

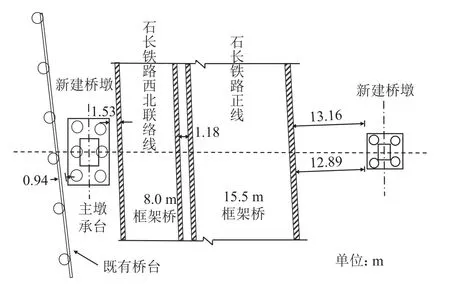
图2 新建桥梁与既有构筑物平面图Fig.2 Plans of new bridges and existing structures

既有绕城高速公路为双向四车道，芙蓉北路采用4×16 m空心板桥跨越绕城高速。桥台为桩柱式桥台，柱径1.2 m，桩径为1.5 m。石长铁路西北联络线采用8.0 m×8.5 m框架桥下穿芙蓉北路，采用C30钢筋混凝土结构，框架边墙及顶板厚度为0.7 m，底板厚度为1.0 m。石长铁路正线采用15.5 m×8.8 m框架箱桥下穿芙蓉北路，框架中心线按直线设置，采用C35钢筋混凝土结构；边墙厚0.9 m，顶板厚0.7 m，底板厚1.0 m；框架与西北联络线框架之间净距为1.18 m。

1.2 控制标准

列车运行引起的振动通过桩基传播到土体，然后传播到附近构筑物引起既有构筑物振动，振动若超过所允许的限值，既有构筑物就有可能发生破坏。变形控制方面，根据《铁路线路维修规则》，框架桥变形控制值应按轨道经常保养的标准控制，水平方向变形不应超过4 mm。速度控制标准方面，《建筑工程容许振动标准》（GB 50868—2013）规定对于振动敏感的构筑物基础容许振动值为2.5 mm/s。加速度控制方面，《城市轨道交通引起建筑物振动与二次辐射噪声限值及其测量方法标准》（JGT/T170—2009）确定位于交通干线两侧的建筑物的振动加速度限值为6.0 mm/s2。根据以上所述，各指标界限值见表1。

表1 结构振动控制标准Tab.1 Structural vibration control standards

2 有限元数值模拟分析

2.1 模型建立

采用MIDAS/GTS对地铁运营荷载作用下框架桥和桥台的受力变形特性进行动态数值模拟。根据工程概况，对总体模型计算区域的选择综合考虑桩基运营所引起的边界效应，确定模型长×宽×高为100 m×60 m×80 m。模型侧面为黏性边界，底面为位移边界，顶面为自由边界，在框架桥和桥台区域进行网格加密，共划分47 815个单元，36 192个节点，有限元模型如图3所示。

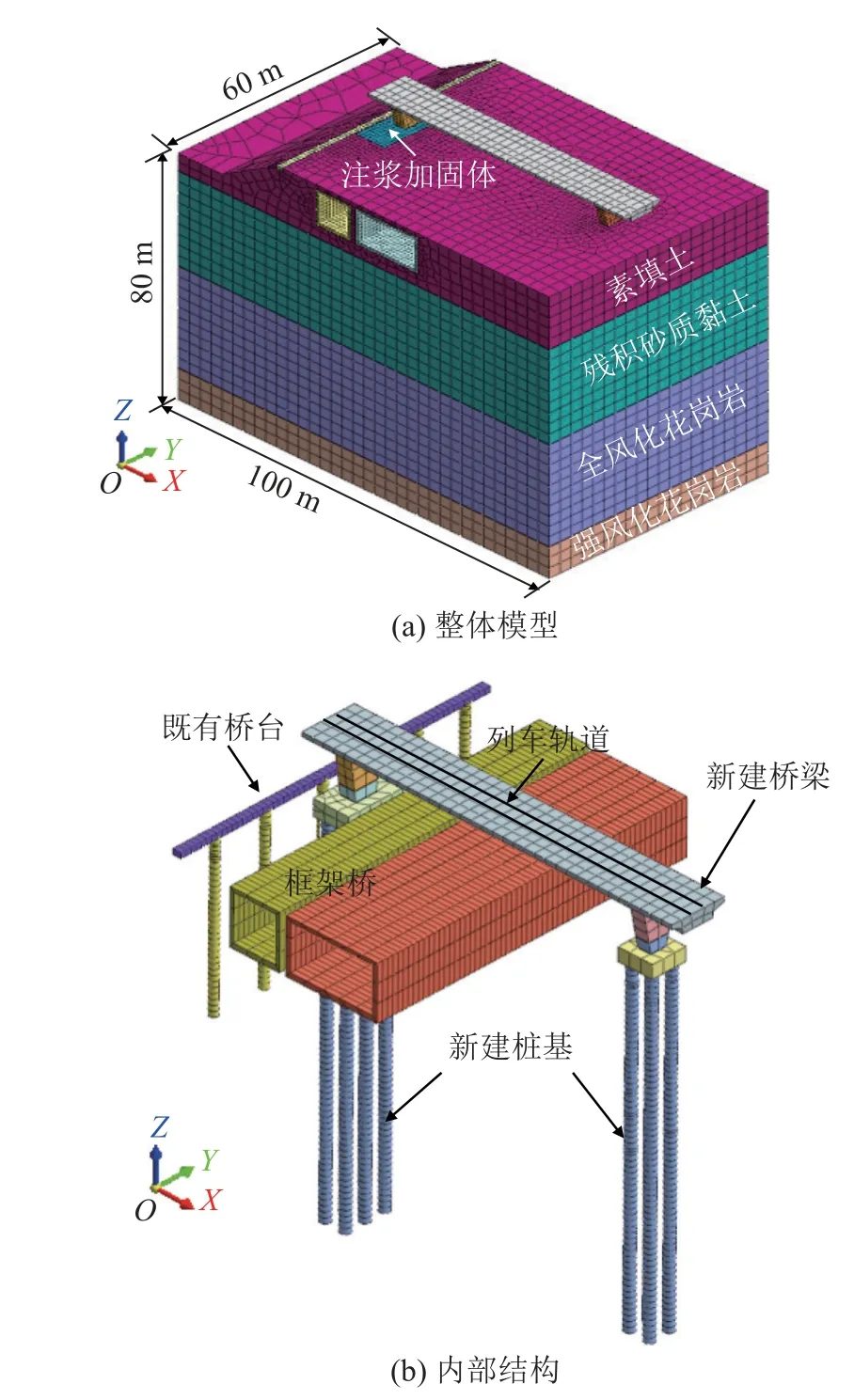
图3 有限元模型示意图Fig.3 Schematic of finite element model

模型中，土体的应力应变特性服从摩尔-库伦准则，桩基础采用1维梁单元模拟并添加桩端单元，材料为C35混凝土。承台、桥墩、桥板、桥台均采用弹性实体单元模拟，材料为C40混凝土。此外，为模拟桩基与土体的相互作用，在桩-土接触面上设置接触单元，模型采用动力分析中常用的瑞利阻尼。根据文献[23-24]可知，土的动静弹性模量之比为5～13，本文取为10。结合地勘资料，材料的物理力学参数如表2所示。

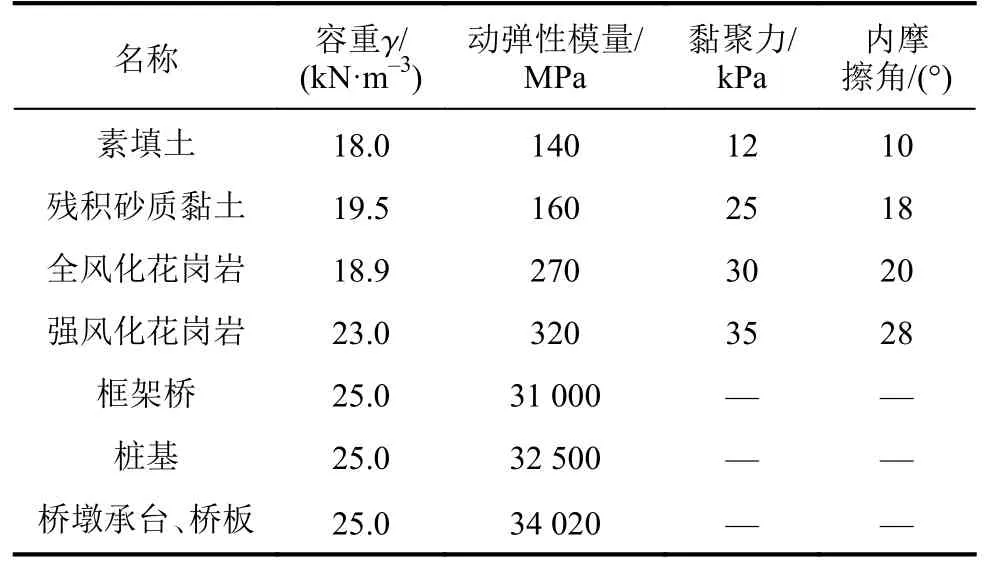
表2 土体及结构计算参数Tab.2 Calculation parameters of soil and structure

2.2 动力边界条件和特征值分析

实际工程中，结构处于半无限空间体中，为消除振动波在模型边界处的反射，需设置符合实际情况的边界条件进行分析，以保证模拟结果的可靠性。

首先，进行特征值分析，研究结构本身的振动特性。将边界定义为弹性边界，根据《铁路线路设计规范》（TB10099—2017）计算边界弹簧值，其竖向和水平地基反力系数如式（1）、（2）所示，通过特征值分析获得第一和第二主振型周期分别为0.63和0.58 s。

2.3 列车荷载模拟

本区间列车类型为广泛采用的标准B2型车，设计行车速度为80 km/h；每列车6辆编组，其中，4辆为动车，2辆为拖车。每编组有4条轮对，每列车共有24条轮对。本文采用24组轴荷载（140 kN）模拟长沙地铁1号线B型车车轮荷载，加载模型如图4所示；地铁运营速度为80 km/h的荷载时程曲线如图5所示。

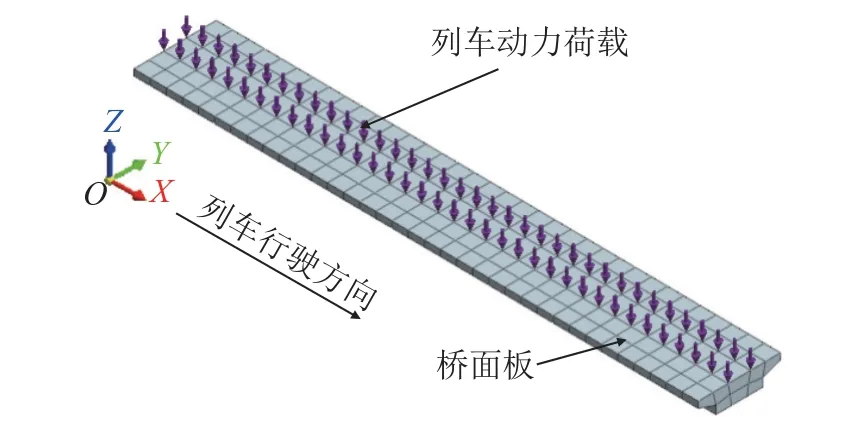
图4 列车动力荷载示意图Fig.4 Schematic diagram of train dynamic load

图5 列车荷载时程曲线Fig.5 Train load time-history curve

2.4 计算工况设置

为研究列车运营荷载参数、近接距离及注浆加固措施对既有结构的影响，设置5种不同工况，分别对运营速度、轴重、与框架桥距离、地层模量及阻尼比进行分析，具体见表3。

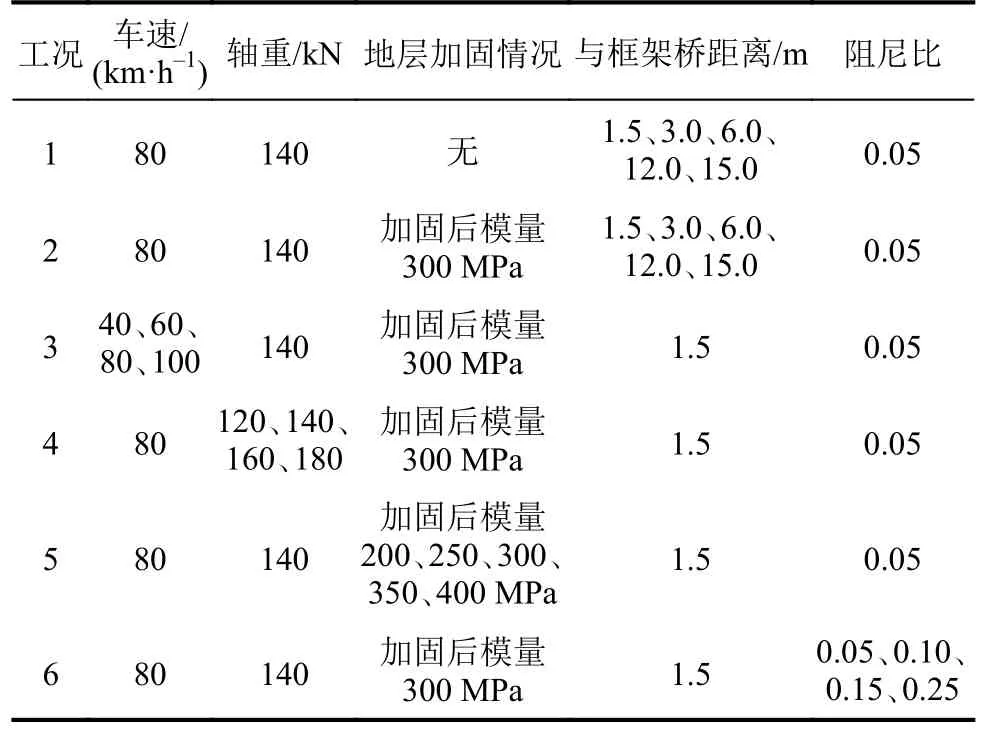
表3 计算工况Tab.3 Calculation conditions

表3中，注浆加固为袖阀管地面注浆，采用水泥-水玻璃双液浆，范围为新建承台两侧不小于2.5倍桩径，宽度为8 m，深度为15 m。

2.5 模型验证

为验证模拟结果可靠性，结合文献[25]西安地铁4号线近距穿越古建筑群工程，建立3维数值振动模型，采用文献中土体及结构的物理力学参数。图6为列车振动荷载作用下护城河桥体峰值振动速度计算结果的对比分析。由图6可知，本文模拟结果与文献[25]计算结果基本吻合，表明本文建模方法可靠。

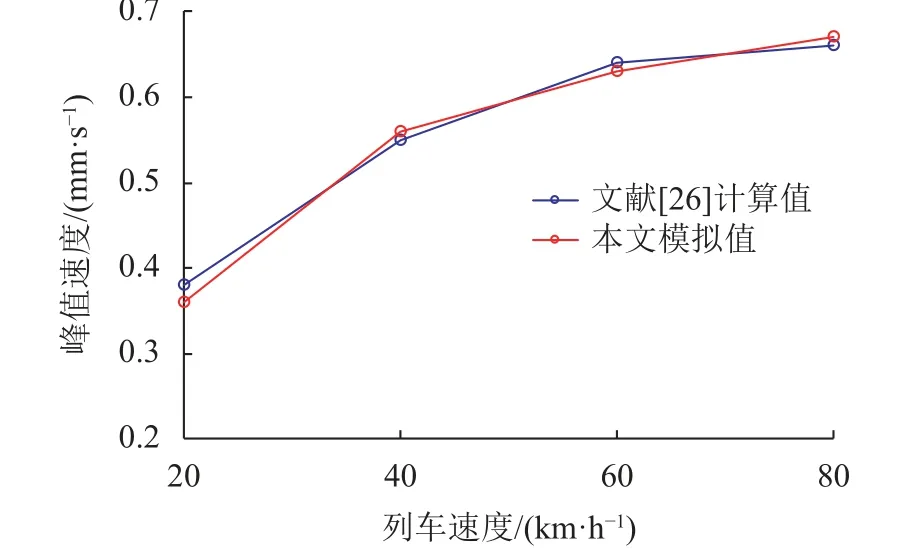
图6 振动峰值速度与文献[25]对比分析Fig.6 Comparative analysis of peak vibration velocity with literature [25]

3 计算结果分析

3.1 地层变形分析

以工况3中车速为80 km/h为例进行研究，选取t=0、4.9、8.1 s时（分别对应列车驶入、将要驶离、驶出该区段）的地层沉降和水平位移，如图7、8所示。由图7和8可知：随着列车的行驶，位移峰值逐渐右移，左侧土体位移开始回弹，右侧土体位移逐渐增大。地层沉降大致呈“U”形分布并向上延伸至地表；土体沉降最大值为0.24 mm，水平位移最大值为0.60 mm。

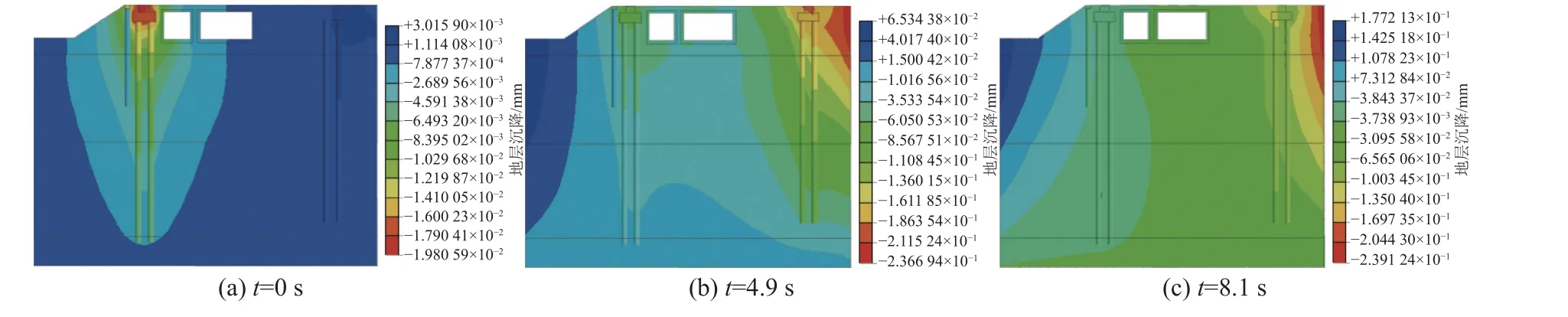
图7 地层沉降云图Fig.7 Stratum settlement cloud map

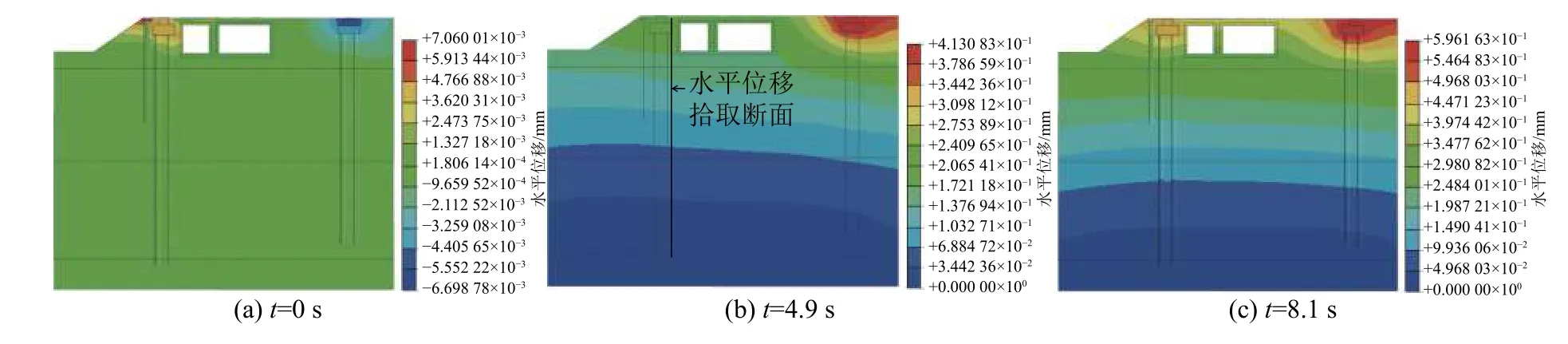
图8 地层水平位移云图Fig.8 Stratum lateral displacement cloud map

选取t=4.9 s时的计算结果，绘制地表沉降与水平位移曲线如图9所示。由图9可知：列车运营时地表沿列车行驶方向产生位移，且水平位移大于地表沉降；水平位移与沉降相比，沉降值是水平位移的40%左右，即列车运营时，地层变形以水平位移为主。

图9 地表沉降和水平位移Fig.9 Surface settlement and horizontal displacement

图10为t=4.9 s时，不同轴重下，新建桩基与框架桥间断面（图8（b））的地层水平位移随深度的变化曲线。

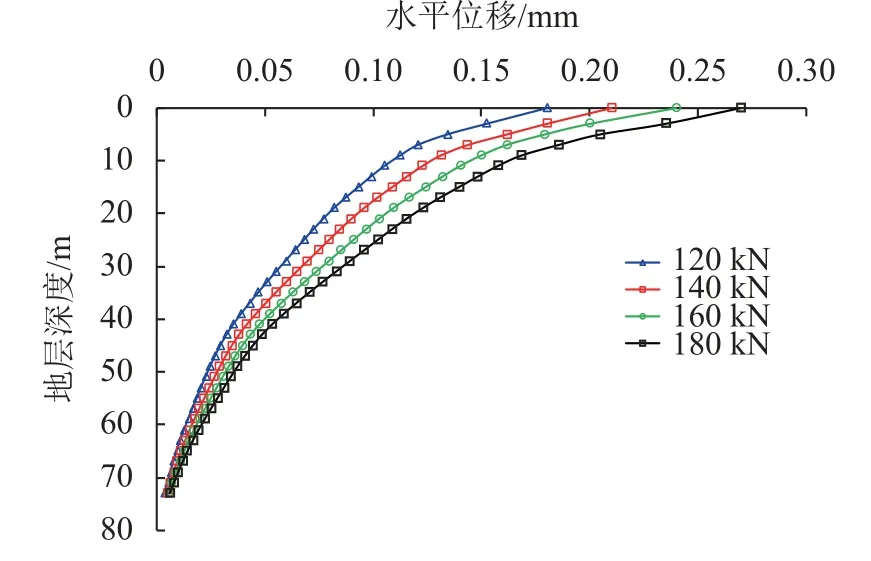
图10 地层水平位移随深度变化曲线Fig.10 Lateral displacement of the stratum in the depth direction

由图10可以看出：不同轴重下的地层水平位移呈现出相同的规律，水平位移随深度的增加而逐渐减小；轴重越大，水平位移就越大。桩基在运营阶段承受荷载时，桩和土之间的摩擦会使周围土体产生水平位移与竖向沉降，导致桩周土体应力场改变，继而会对既有构筑物造成影响，与桩基的距离越近，所受到的影响就越大。

3.2 时程分析

由文献[8]可知，既有构筑物在新建桥运营期主要受其与新建桥的距离影响。图11为动力响应监测点布置。图11中，编号1～6为既有桩基编号，a、b、A、B为监测点。

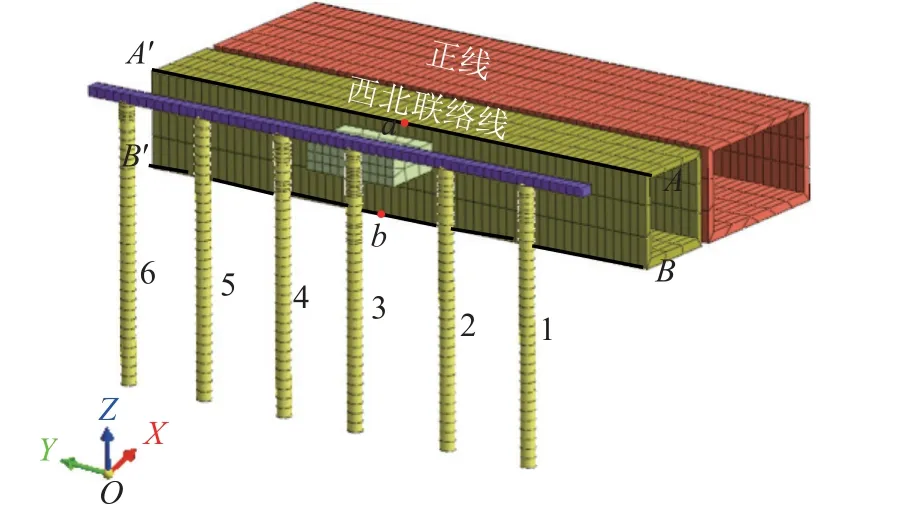
图11 监测点布置Fig.11 Layout of monitoring points

为分析桥台和框架桥结构不同位置的动力响应特性，以工况3中车速80 km/h为例进行研究，桩顶、3号桩和框架桥的动力响应时程曲线如图12、13、14所示。

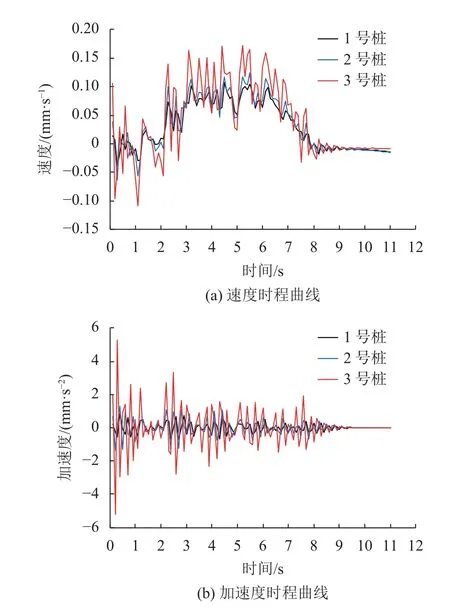
图12 不同桩顶动力响应Fig.12 Dynamic response of different pile tops

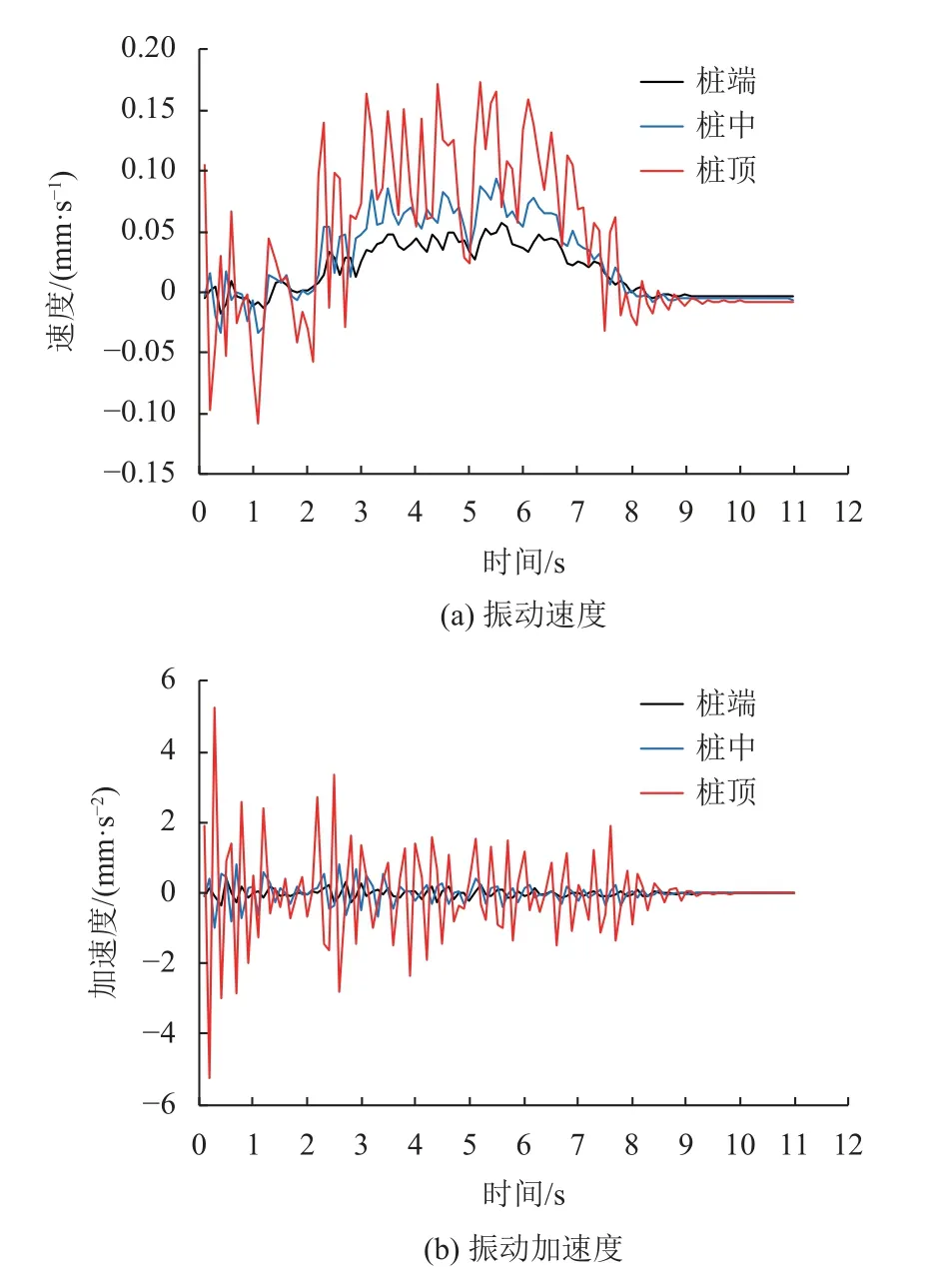
图13 3号桩不同深度处动力响应时程曲线Fig.13 Dynamic response time-history curves of No.3 pile at different depths

图14 框架桥动力响应时程曲线Fig.14 Dynamic response time-history curve of frame bridge

由图12、13、14可知：各监测点的振动速度整体上随着时间先增强后减弱，即随着列车的靠近而逐渐增大，随着列车的远离而逐渐减小，列车全部作用在桥梁时响应较大。振动加速度随时间逐渐减弱，在t=0～1 s时响应较大。

3号桩桩顶的动力响应最为强烈，其振动加速度明显大于2号桩和1号桩，振动峰值加速度分别为5.26、1.29、0.84 mm/s2；对应的衰减幅度依次为75.4%和34.8%，即动力响应从3号桩到2号桩衰减较快，从2号桩到1号桩衰减较慢。

随着深度的增加，桩基的振动速度和振动加速度幅值均逐渐减小。桩顶、桩中和桩端的振动峰值速度分别为0.17、0.09、0.05 mm/s，从桩顶至桩端，振动速度整体衰减了70.5%；峰值加速度分别为5.26、0.82、0.41 mm/s2，有明显衰减。这是由于土体阻尼导致动力响应在传播过程中衰减，在一定深度范围内衰减较大，超过一定深度衰减变缓。框架桥测点a、A、b、B的峰值速度分别为0.15、0.12、0.09、0.08 mm/s，框架桥动力响应呈现出顶板大于底板的规律。在长期的通车运营中，桩顶和框架桥顶板受运营荷载影响更为显著，应重点关注。

3.3 速度的影响

在工况3情况下，选取3号桩的桩顶、桩中、桩端和框架桥监测点在不同车速下的峰值位移、振动峰值速度、振动峰值加速度，结果如图15、16所示。

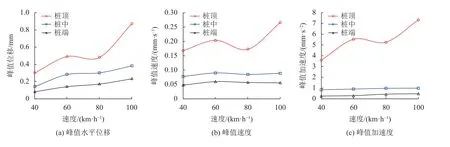
图15 列车速度对3号桩动力响应的影响Fig.15 Influence of train speed on the dynamic response of No.3 pile

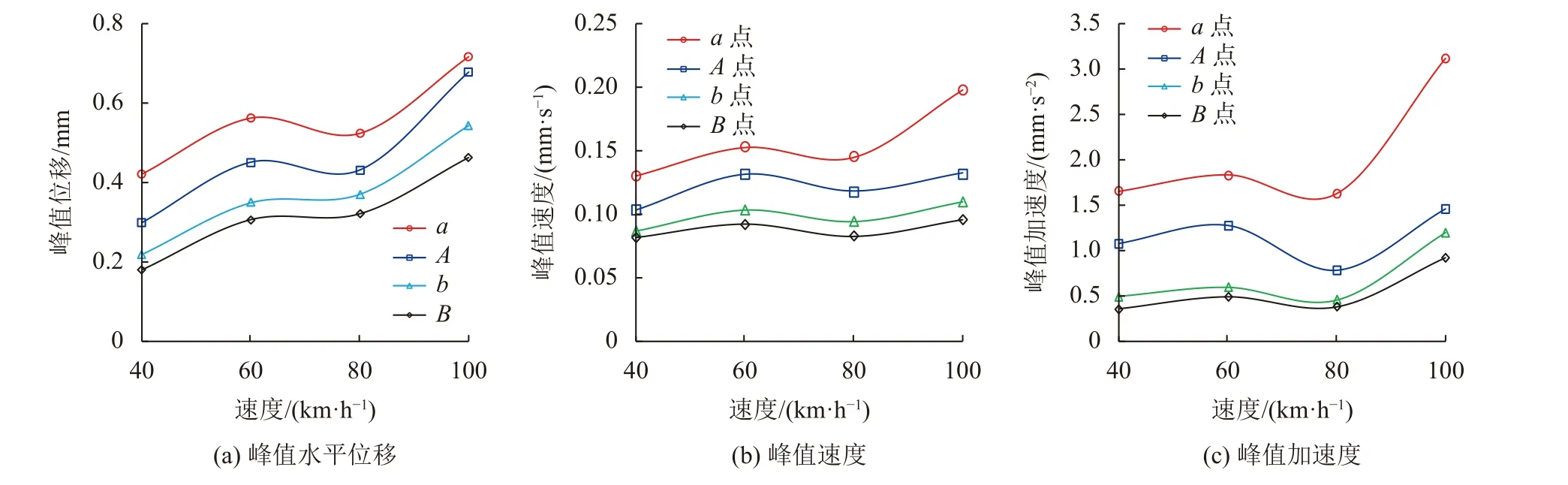
图16 列车速度对框架桥动力响应的影响Fig.16 Influence of train speed on the dynamic response of frame bridge

由图15、16可知，随着列车速度增加，既有构筑物的动力响应并不是线性增大，在一定速度范围内甚至存在降低的情况。原因主要与激振频率和荷载作用时间等因素有关，低速列车荷载激振频率低，荷载变化慢，作用时间较长，对结构的影响可能会较大；高速列车产生的激振频率虽然较大，但作用时间短，对结构的影响也可能较小。这些因素同时共存，此消彼长，与文献[26]的研究结果一致。

桩顶动力响应受列车速度变化的影响最大，桩中和桩端受列车速度变化影响较小。振动速度当列车从80 km/h到100 km/h时变化较快，从40 km/h到80 km/h时变化缓慢，这是由于不同的波在相同材料中传播的衰减规律不同。框架桥底板的速度、加速度随列车速度提高的变化趋势比顶板要缓。既有结构的峰值位移、峰值速度、峰值加速度在v=80 km/h附近有先减小后增大的趋势，因此v=80 km/h为最佳运行速度，此时桩基和框架桥峰值位移、峰值速度、峰值加速度分别为0.48 mm、0.17 mm/s、5.26 mm/s2和0.52 mm、0.15 mm/s、1.67 mm/s2。对于运营速度较快的列车，其激振频率的提高加大了既有结构的振动加速度，对既有结构产生了不良的影响。当车速为100 km/h时，桩顶振动加速度为7.34 mm/s2，超过振动限值要求。整体来看，桩顶和框架桥顶板的峰值速度、峰值加速度变化量较其他部位大，应重点加强监测。

3.4 轴重的影响

图17、18为工况4情况下，不同轴重对既有结构动力响应的影响。由图17、18可知：随列车轴重的增加，既有构筑物的峰值位移、峰值速度、峰值加速度近似呈线性增长，但不同深度处的增长趋势略有不同；桩顶随轴重增加的增幅最大，随着深度的增加，增幅逐渐减小。框架桥顶板的动力响应对于轴重变化最为敏感，底板动力响应随轴重的增幅略有降低。轴重从120 kN增加到180 kN时，桩顶的峰值位移增幅为46%，峰值速度增幅为51%，峰值加速度增幅为50%。轴重为180 kN时，桩顶振动加速度为6.19 mm/s2，超过限值要求。整体来看，桩顶和框架桥顶板受轴重的影响较大。

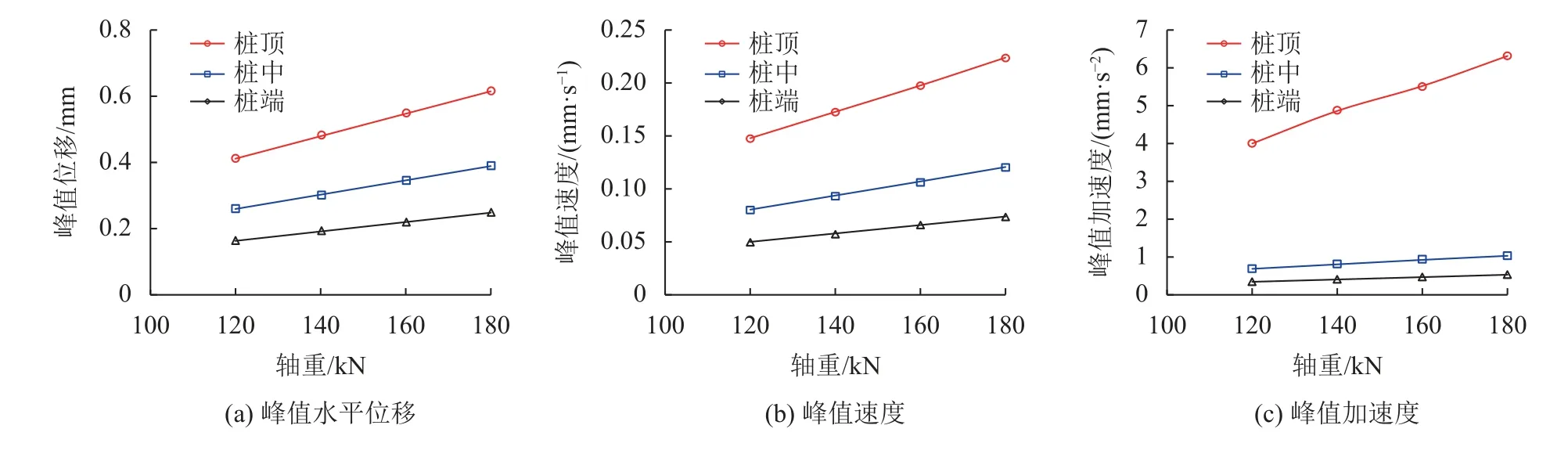
图17 轴重对3号桩动力响应的影响Fig.17 Influence of axle load on the dynamic response of No.3 pile

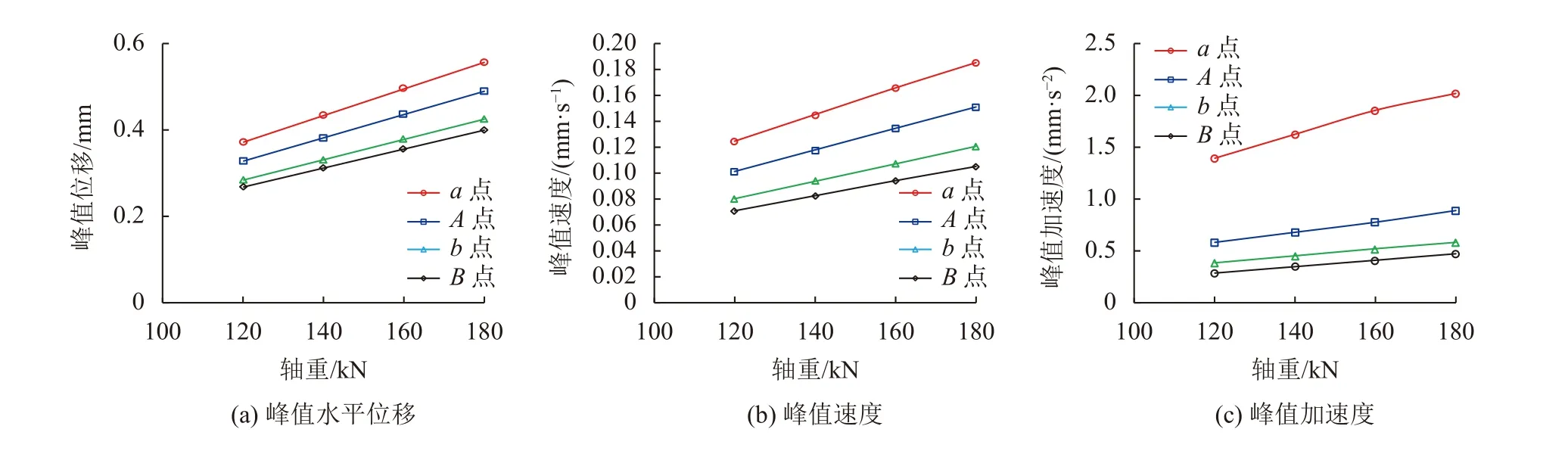
图18 轴重对框架桥动力响应影响Fig.18 Influence of axle load on dynamic response of frame bridge

3.5 近接距离的影响

为研究运营桩基近接距离对铁路框架桥的影响，针对工况1、2，以峰值水平位移和峰值速度为例进行分析，如图19、20所示。

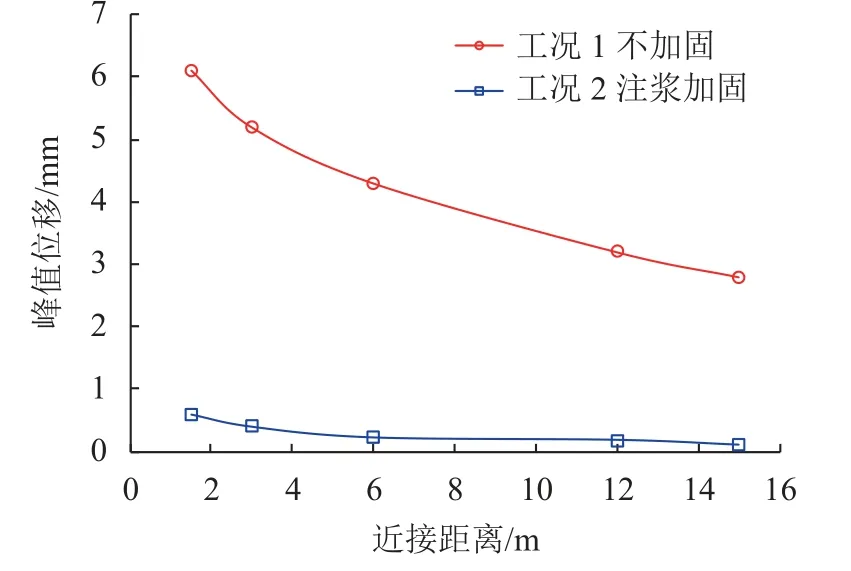
图19 近接距离对水平峰值位移影响Fig.19 Influence of mutual distance on peak lateral displacement

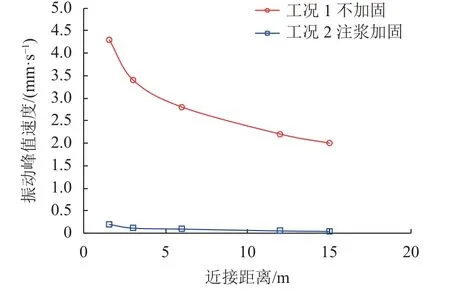
图20 近接距离对振动峰值速度影响Fig.20 Influence of mutual distance on peak vibration velocity

由图19、20可知，在运营期荷载作用下，桩周土产生了侧向位移，继而使框架桥产生横向变形，且朝远离桩基的方向发展。随着近接距离的增大，框架桥的峰值位移和振动峰值速度逐渐减小。由曲线幅度可知，在较近距离时，改变间距可有效减缓桩基运营的影响，较远距离时由间距影响引起的变形差异较小，特别在6 m（即4倍桩径）范围外曲线趋于平缓。这是由于土体作为桩基-框架桥相互作用的媒介，承担着传递地层变形的效果，随着近接距离的不断增大，变形在传递过程中不断衰减，影响程度不断减弱。近接距离为6 m时，峰值位移和峰值速度分别为4.3 mm、2.8 mm/s，超过控制标准要求；采取注浆加固后，由于土体的力学性能提升导致框架桥的峰值位移和振动峰值速度明显减小，分别为0.22 mm、0.10 mm/s，满足要求。因此，建议新建桩基与既有框架桥之间的水平距离不少于4倍桩径，若近接距离较小，则需要采取一定的地层加固措施来保证既有框架桥的安全。

3.6 注浆加固效果分析

由第3.5节知，未加固工况下，近接距离为1.5 m时，峰值位移和峰值速度分别为6.1 mm、4.3 mm/s，超出限值要求，因此，在高架桥上跨工程实际施工中，为减小桩基运营对既有构筑物的影响，对桩基周边土体进行地表注浆加固。分别取加固区刚度为200、250、300、350、400 MPa（工况2），分析对应工况下框架桥的动力响应，结果如图21、22所示。由图21、22可知：随着加固区刚度的增加，框架桥峰值变形和振动峰值速度均明显降低。加固区刚度从200到300 MPa，水平峰值位移平均减小33%，峰值速度平均减小45%；从300到400 MPa，水平峰值位移平均减小14%，峰值速度平均减小21%；加固区刚度达到300 MPa后，这种影响逐渐减弱，继续提高加固区刚度对降低动力响应的效果不明显。

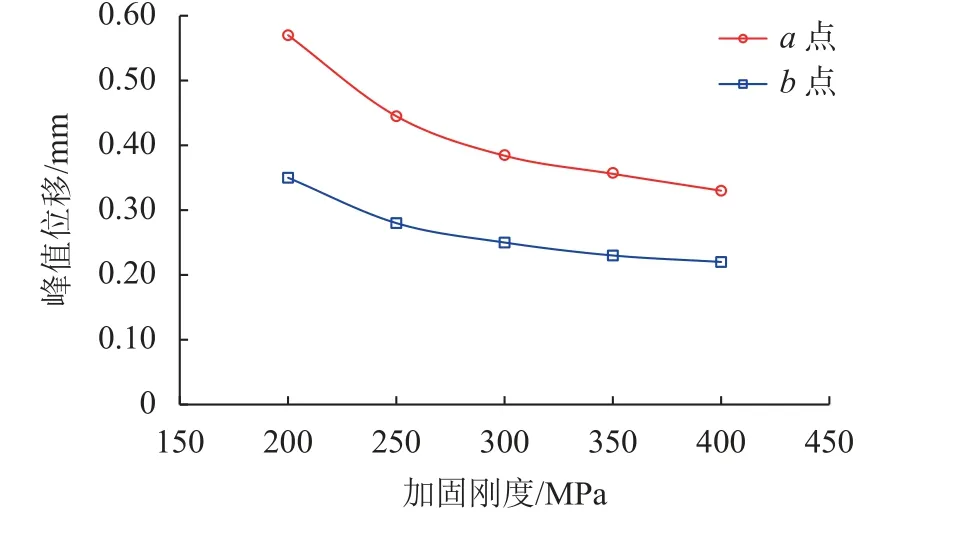
图21 加固刚度对水平峰值位移影响Fig.21 Influence of reinforcement stiffness on peak lateral displacement

图22 加固刚度对振动峰值速度影响Fig.22 Influence of reinforcement stiffness on peak vibration velocity

3.7 土体阻尼系数影响

土体阻尼是进行动力分析和评价必不可少的重要参数，表征土体消耗能量的程度。为研究土体阻尼对构筑物动力响应的影响，选用阻尼比0.05、0.10、0.15和0.25（工况6），以3号桩桩顶振动速度响应为例进行分析，结果如图23所示。由图23可知，阻尼比增大时，振动峰值速度逐渐减小。这表明阻尼比越大，振动在土体中消耗的能量也越大，峰值速度越小。

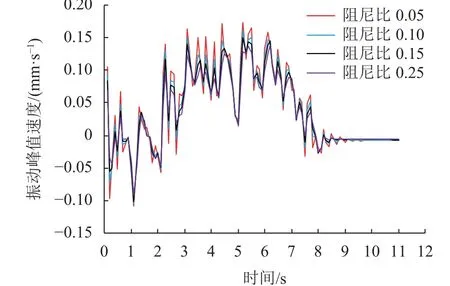
图23 不同阻尼比下振动峰值速度时程曲线Fig.23 Time-history curve of vibration peak velocity under different damping ratios

4 结 论

结合长沙地铁1号线北延线高架桥桩基近接既有桥台和框架桥，建立列车荷载下高架桥-地层-既有结构的3维数值模型，研究了列车运营期荷载作用下既有桥台和框架桥的动力响应特性，得到以下结论：

1）列车荷载作用下地层变形以水平位移为主，既有桥台中间桩基的动力响应最为强烈。不同深度方向上，呈现出桩顶动力响应大于桩中和桩端、顶板大于底板的规律，从桩顶至桩端，振动速度整体衰减约70.5%；长期运营过程中，桩顶和框架桥顶板为不利位置，应予以重点关注。

2）随着列车速度的增加，既有结构的动力响应并不是呈线性增大趋势，而是在一定时速内存在波动状态；且在低速区时变化幅值较小，超过一定时速，则加速增长，最佳运行速度为80 km/h；桩顶及框架桥顶板受车速变化的影响较大。

3）列车轴重与既有结构的动力响应呈线性增大的关系；新建桩基与框架桥的近接距离越小，变形与振动峰值速度就越大；随着距离的增加，振动有所衰减，超过一定距离衰减变缓。建议新建桩基与框架桥之间最小水平距离不低于新桩桩径的4倍。

4）既有构筑物动力响应随加固区刚度和阻尼比的增加而减小；加固区刚度达到300 MPa时，继续提高加固区刚度对降低动力响应的效果不明显。