例析中考代数推理题及其教学反思*

吴 琨

⦿ 江苏省南京市上元中学

1 代数推理的重要性与含义

《义务教育数学课程标准(2022年版)》(以下简称《2022年版课标》)指出,推理能力是数学核心素养的主要表现之一,有助于学生逐步养成重论据、合乎逻辑的思维习惯,形成实事求是的科学态度与理性精神[1].

《2022年版课标》对初中阶段推理能力的内涵界定如下:“推理能力主要是指从一些事实和命题出发,依据规则推出其他命题或结论的能力.”由此,新课标把培养目标中的数学思维表述为“主要表现为运算能力、推理意识或推理能力”.其中,运算本质上就是演绎推理[2].所以,在这个意义上可以认为,培养目标中的数学思维主要表现为推理,推理集中反映了数学思维的共通育人要求和独特育人价值[3].

在日常的数学教学中,有高中教师反映,初中生代数领域的推理能力难以应对高中阶段代数学习的要求.对此,《2022年版课标》在代数式这一部分内容增加了“了解代数推理”,近年来考查学生代数推理能力也已逐渐成为中考的一个新的考查方向.

2 从中考题看代数推理的解题思路

2.1 演绎推理

例1(2021年·江苏南京)设x1,x2是关于x的方程x2-3x+k=0的两个根,且x1=2x2,则k=______．

解析：根据根与系数的关系,可得x1+x2=3,x1x2=k,再结合题目已知条件x1=2x2,可得k=2.

评析：本题是运用演绎推理解决问题,即从一般性原理出发,推出某特殊情况下结论.首先是已知的一般原理(大前提),即根与系数的关系;其次,存在所研究的特殊情况(小前提),即x1+x2=3,x1x2=k,x1=2x2;最后得出特殊情况下的结论.

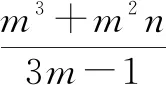
解析：因为m是一元二次方程x2+3x-1=0的根,所以m2+3m-1=0,则3m-1=-m2.

因为m,n是一元二次方程x2+3x-1=0的两个根,所以m+n=-3.

评析：本题也是代数演绎推理的运用.在求解时,首先要知道运用哪些大前提(根与系数的关系,等式与分式的基本性质),然后再根据题目中的小前提(m,n是一元二次方程x2+3x-1=0的两个实数根)进行求值.在求解中,可以利用整体代换、降次等变形技巧.

小结：例1、例2都是考查学生代数演绎推理能力.演泽推理的基本形式为“三段论”,即大前提—小前提—结论.这既能培养学生自主探究的能力,又能培养学生演绎推理的能力.学生在日常学习中就要注重问题的探求过程,体验知识“数学化”的过程,要学会用严谨的数学语言进行表达.以上演绎推理是通过相关运算进行的,属于算数推理或代数推理.

2.2 归纳推理

例3(2022年·江苏宿迁)按规律排列的单项式x,-x3,x5,-x7,x9,……,则第20个单项式是______．

解析：第1个指数为2×1-1=1,第2个指数为2×2-1=3,第3个指数为2×3-1=5,……,第n个指数为2n-1;并且,第偶数个单项式的系数为-1.

所以第20个单项式是-x39.

评析：本题考查的知识点是单项式的系数与次数的含义,关键是通过归纳与总结得到单项式的系数与次数的规律.通过代数运算发现指数规律,掌握“从具体到一般的探究方法”.

例4(2021年·江苏扬州)将黑色圆点按图1所示的规律进行排列,图中黑色圆点的个数依次为1,3,6,10,……,将其中所有能被3整除的数按从小到大的顺序重新排列成一组新数据,则新数据中的第33个数为______．

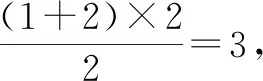
小结：例3、例4都是合情推理中归纳方法的应用.归纳是通过对某类事物中若干特殊情形的分析得出一般结论的思维方式.解决此类推理题的关键与难点就是归纳出题干中所隐含的规律.学生要学会通过几个特例,归纳出蕴含在部分对象之中的共同性质,从而发现规律,要求学生用数学符号表达自己的想法.此归纳推理是通过运算进行的,即属于算数推理或代数推理.

2.3 类比推理

例5(2020年· 江苏徐州)阅读感悟:有些关于方程组的问题,欲求的结果不是每一个未知数的值,而是关于未知数的代数式的值,如以下问题:

已知实数x,y满足3x-y=5①,2x+3y=7②,求x-4y和7x+5y的值．

本题常规思路是将①②两式联立组成方程组,解得x,y的值再代入欲求值的代数式得到答案,常规思路运算量比较大．其实,仔细观察两个方程未知数的系数之间的关系,本题还可以通过适当变形整体求得代数式的值,如由①-②可得x-4y=-2,由①+②×2可得7x+5y=19．这样的解题思想就是通常所说的“整体思想”．

解决问题:

(2)某班级组织活动购买小奖品,买20支铅笔、3块橡皮、2本日记本共需32元,买39支铅笔、5块橡皮、3本日记本共需58元,则购买5支铅笔、5块橡皮、5本日记本共需多少元?

分析：(1)由已知2x+y=7①,x+2y=8②,利用 “整体思想”,①-②即可求得x-y的值,①+②即可求得x+y的值.

(2)设每支铅笔x元,每块橡皮y元,每本日记本z元,根据题意列出方程组,结合“整体思想”,类比材料中的方法即可求解．

评析：通过阅读材料,领悟“整体思想”在解题中的应用,类比此方法求解第(1)小题,抓住两个方程未知数的系数之间的关系,进行合理变形,即可得到含x+y,x-y的式子;对于第(2)小题,引入x,y,z后,得到20x+3y+2z=32,39x+5y+3z=58,类比材料中的方法,通过整体变形得到含“5x+5y+5z”的式子,以此求得它的值.以上第(1)(2)小题的求解就体现了类比推理.

小结：例5是类比推理的应用,解答类比推理题的关键就是运用熟悉的数学知识点,用类比的方法,分析未知与已有的认知结构中具有的相似特征,然后猜想其解题方法和解题思维上的类似之处,从而解决问题.应用类比推理方法可以培养学生的思维能力,对问题进行更深层次的认识,在做题时能缩短做题时间,提高做题效率.此类比推理是通过运算进行的,亦属于算数推理或代数推理.

3 教学反思

中考数学中的代数推理题综合性强,形式比较新颖,解题方法灵活多变.那么,初中教师应如何有意识地培养学生的代数推理能力呢?

(1)教师要纠正教学认知.在应试导向的教学实践中,教师往往会倾向于如何“高效”地把解题具体策略、手段或方法硬塞给学生,导致推理的教育意义很难在这种依赖被动的“灌输”中生长.甚至学生误以为在基础教育阶段几何证明等同于推理,导致对新课标提出的“三会”中的数学思维主要表现的推理,特别代数推理,仍然感觉陌生而难操作.

(2)教师要抓住教学中的每个关键时期,抓住一切可以示范的机会进行训练,完善学生代数推理的表达体系,常用“因为……,所以……”“之所以……,是因为……”“因此”“由此可见”等作为推理的词组[4].

(3)教师应该重视演绎推理、归纳推理和类比推理,在教学中多加运用,经常性渗透.比如,演绎推理——从有理数、整式和分式运算,到方程、不等式和函数,代数演绎推理几乎涉及所有初中代数内容.举例说明,由方程2x+3=5怎么得到x=1?首先方程两边同时减去3,得到2x=2,然后方程两边同时除以2,得到x=1.这里运用的就是演绎推理,主要依据是等式的基本性质.再如,归纳推理——在某些数学概念的教学过程中,可以引导学生从特殊事物的各不同属性中归纳出共同的、本质的属性,在此基础上形成定义.这就是归纳推理的一种运用.类比推理在初中数学教学中应用得也很多,如,分数的运算与分式的运算,因数分解与因式分解,一元二次方程和二次函数,等等.如果在教学中运用类比推理,既能减少学生对数学知识的陌生度,又能让学生达到温故而知新的目的,还可以培养学生的思维能力,使整个数学教学有事半功倍的效果.

总之,代数推理是培养学生抽象能力、推理能力,发展学生逻辑思维与理性精神的良好载体.在教学中教师需提高认识,系统开发和设计相应素材资源,适时适地地让学生经历各类代数推理过程,感悟代数推理的真谛,提升数学素养.