透析试题本质,用问题驱动提升学习力*——基于圆的试题生成分析与教学思考

刘 欣

⦿ 湖北省武汉市武昌区教育局教研培训中心

由圆外一点引圆的两条切线所构成的图形是一个轴对称图形,具有轴对称图形的特殊性质,提炼这个基本图形及变式图形所隐含的特殊结论,并运用于解决新问题,是提升数学综合能力的有效方式.笔者研究武汉市近年来的各类考题,探索含此基本图形的试题的本质特征,运用这些结论解题都可以让问题迎刃而解.因此,透析试题本质,寻找问题与基本图形之间的联系,可以轻松找到解决问题的途径.《义务教育数学课程标准(2022年版)》强化了“如何教”的具体指导,要促进学生深度参与教学,必须在精心设计问题的同时,巧妙呈现提出问题的方式,让学习探究在不断生成的问题解决中逐步展开,这样才能有效促进学生数学学习力的提升.

1 试题背景

如图1,过圆外一点P作⊙O的两条切线PM,PN,切点分别为A,B.连接OA,OB,则∠APB+∠AOB=180°.

在图1的基础上,连接OP,AB,AB交OP于点Q,如图2,分别从角与角、线段与线段、三角形与三角形的关系分析,可以得到如下结论:

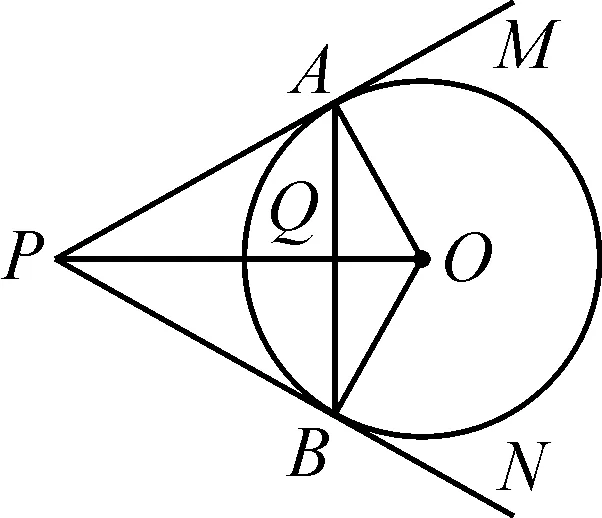
图2

(1)∠APO=∠BPO=∠OAB=∠OBA.

(2)PA=PB,AQ=BQ,PO⊥AB.

(3)△OAP≌△OBP,△APQ≌△BPQ;△OAQ∽△APQ∽△OPA等.

延长AO交⊙O于点C,交PN于点D,连接BC,如图3,又可以得到以下结论:

图3

(4)∠ACB=∠AOP=∠PAB,BC∥PO;

(5)△DBC∽△DAB;

(6)△ABC∽△PAO∽△AQO∽△PQA等.

2 试题演变及解析

上面的三个图形和相关结论,经常被各地用于命制各类试题,研究近几年武汉市的调考和中考试题,可以发现它们之间的联系和变式生成过程.

2.1 取圆上一点,构造圆周角,运用角的关系求角

例1(2022年武汉元月调考)如图4,PM,PN分别与⊙O相切于A,B两点,C为⊙O上异于A,B的一点,连接AC,BC.若∠P=58°,则∠ACB的大小是______.

图4

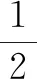
图5

故填答案:61°或119°.

2.2 取圆上一点,添加角和线段,求半径

图6

分析及解：如图7,连接OA,OP,AB,作BD⊥AC于点D.

图7

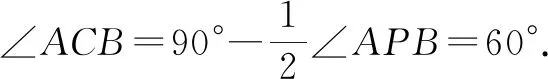
由∠MAC=75°,得∠BAC=45°.

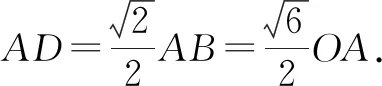
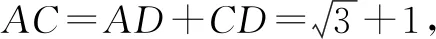
2.3 构造直角三角形,把已知线段和角转移到直角三角形中

例3(2016年武汉四月调考)如图8,在Rt△ABC中,∠ACB=90°,点O在BC上,以点O为圆心,OC为半径的⊙O刚好与AB相切,交OB于点D.若BD=1,tan∠AOC=2,则⊙O的面积是( ).

图8

分析及解：设⊙O的半径为r,AB与⊙O相切于点E,连接DE,则DE∥OA.

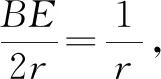
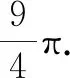
2.4 已知过圆外一点的一条切线,画出另外一条切线,再证明判断并赋值求解新问题

例4(2011年武汉中考)如图9,PA为⊙O的切线,A为切点,过点A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与PA的延长线交于点E.

图9

(1)求证:PB为⊙O的切线;

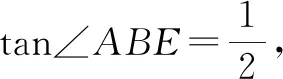
分析及解：(1)如图10,连接OA.

图10

由△OAP≌△OBP,得∠OBP=∠OAP=90°.

所以PB是⊙O的切线.

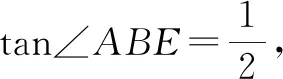
设DE=m,则

由试题背景中的结论(3),知△ABE∽△DAE.

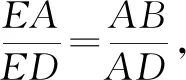
2.5 构造等腰直角三角形,运用特殊结构,建立特殊情况下的比值问题

例5(2020年武汉元月调考)如图11,PA,PB分别与⊙O相切于A,B两点,AC是⊙O的直径,AC=AP,连接OP交AB于点D,连接PC交⊙O于点E,连接DE.

图11

(1)求证:△ABC≌△PDA;

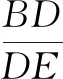
分析及解：(1)由∠PDA=∠ABC=90°,∠PAD=∠ACB,PA=AC,得△ABC≌△PDA.

(2)连接AE,BE.由△ABC≌△PDA,得BC=DA.

由AC是⊙O的直径,得AE⊥CP.

又AC=AP,所以CE=PE=AE.

又∠BCE=∠DAE,所以△BCE≌△DAE.

3 关于“如何教”的思考

对于试题解析教学“怎么教?”的问题,既要分析试题之间的联系和试题的本质,还要有好的教学呈现方式,把试题化为一个个问题,不断变式,逐级推进,带动学生参与到解决问题的过程中,让学生经历观察、思考、表达、概括归纳、迁移运用的学习过程,促进数学素养的形成与发展.

3.1 画基本图形,探索一般结论

问题1过圆外一点P作⊙O的两条切线PM,PN,切点分别为点A,B.如图12,连接OA,OB,你能发现∠APB与∠AOB有什么关系?

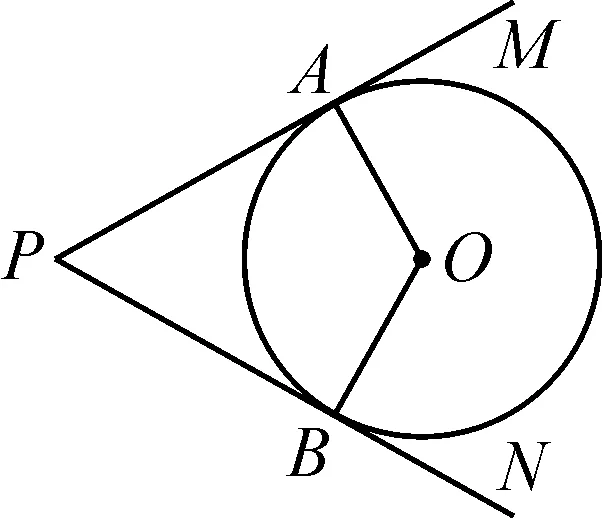
图12

问题2在图12的基础上再连接OP,AB,AB交OP于点Q,如图13,你能发现图中角与角、线段与线段,三角形与三角形有什么关系?

图13

问题3在图13的基础上延长AO交⊙O于点C,交PN于点D,连BC,如图14,你又可发现哪些新结论?

图14

教学说明：设置这3个问题,从具体的问题1到开放的问题2、问题3,教学时先不给出图形,让学生通过对问题的文字和符号语言的理解自己画图,感受图形生成过程,再研究图形的几何特征进而发现结论.

3.2 变换基本图形,呈现试题生成过程

(Ⅰ)基于问题1,给出∠P的度数,求圆周角.

问题4在问题1的基础上,在⊙O上取一点C(异于点A,B),连接AC,BC.若∠P=58°,能求出∠ACB的度数吗?

(Ⅱ)基于问题1,给出角和线段的值,求半径.

图15

(Ⅲ)由问题3演变,设置条件,求⊙O的面积.

问题6在上述问题3的基础上,若CD=1,tan∠AOP=2,你能求出⊙O的面积吗?

(Ⅳ)改变问题1的条件,已知圆的一条切线,呈现另外一条切线的作图过程,再判断切线,并添加已知条件设置新问题.

问题7如图16,PA为⊙O的切线,A为切点,过点A作OP的垂线AB,垂足为点C,交⊙O于点B,延长BO与⊙O交于点D,与PA的延长线交于点E.

图16

(1)求证:PB为⊙O的切线;

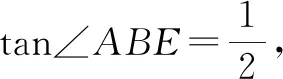
(Ⅴ)保留PA,PB与⊙O相切,添加条件构造等腰直角三角形,生成新问题.

问题8如图17,PA,PB分别与⊙O相切于A,B两点,AC是⊙O的直径,且AC=AP,连接OP交AB于点D,连接PC交⊙O于点E,连接DE.

图17

(1)求证:△ABC≌△PDA;

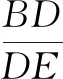
教学说明：用以上问题4～8把前面的5个例题串联了起来,通过从圆外一点引圆的两条切线所构成的基本图形,添加线段,增设条件,形成新问题,让学生既能感受到试题生成的过程,又能在一个个问题的带动下参与探究解决问题的过程.教学时注意问题要一个一个呈现,让学生在解决前一个问题后,再观察教师添线画图、设置条件、生成新问题的过程,让学生的思维参与到图形的生成、问题的变式过程中,感受到问题的不断生长,这样才能激发学生的学习动力,驱动学生深度参与探究学习,培养数学能力和素养.

4 结语

《义务教育数学课程标准(2022年版)》要求我们要整体把握教学内容之间的关联,注重情境设计与问题提出,在真实情境中提出引发学生思考的问题,从而促进学生积极探究[1].因此,在试题解析教学中,不能简单地呈现试题直接让学生求解,要注意把试题问题化,在分析试题之间的联系与本质之后,教学时用问题把试题串起来,通过在基本图形背景基础上,添加图形条件,设计一个个螺旋上升不断变式的问题,引导学生具体画图观察、自主探究解题途径、亲身经历试题变式过程,从而透析问题本质,揭示试题之间的联系,有效提升数学学习力,促进数学核心素养的发展.