面向几何直观的代数推理——以初中学段函数作图内容为例

黄邵宏 王光生

⦿ 陕西师范大学数学与统计学院

1 问题提出

核心素养具有整体性、一致性和阶段性,在不同阶段具有不同的表现.《义务教育数学课程标准(2022年版)》提出了初中阶段数学核心素养的九种表现形式,其中包含几何直观和推理能力.

数学核心素养之间是密不可分、相辅相成的,几何直观和推理能力亦然.直觉与逻辑的完美结合是数学发展与学生思维发展的根本之道,应该追寻直觉背后的逻辑与引领逻辑的直觉.在培养学生几何直观素养的同时,也要注重学生逻辑推理素养的协同发展,更需要挖掘二者之间的联系,以促进学生思维的发展.代数推理是逻辑推理素养的重要组成部分,几何直观同样也是直观想象的关键部分.由于初中学段尚未提出核心素养的概念,本研究聚焦代数推理和几何直观.为此,培养学生关键能力,厘清二者之间的脉络至关重要.本研究从初中学段函数内容出发,例说代数推理对几何直观的促进作用,把几何直观视为代数推理的起点之一.

函数是中学数学课程内容的主线之一,也是学习的关键.依据初中数学学习的知识序,学生先学习函数的解析式,再利用列表、描点、连线三部曲,作出函数的图象.由此,引发一些思考:

(1)这种作图方法针对简单的一次函数尚可,对于更深层次的反比例函数、二次函数等如何恰当列表?

(2)为何有的函数图象是直线,有的函数图象是曲线,有的函数图象只是一些点?

(3)反比例函数、二次函数描点以后,为何使用光滑的曲线而非折线来连接?

如果能够先对函数解析式进行简单的代数推理,猜出函数的大致图象,就能恰当把握好列表、描点、连线的过程,进而得到精准的函数图象,同时对后续高中、大学学段函数模块学习提供很大的帮助.

2 案例展示

2.1 正比例函数图象的教学——猜图象

已知正比例函数解析为y=kx(k≠0),不妨设k>0,此时可取y=2x.

根据表1中的推理,猜出函数y=2x的图象如图1所示.

图1

作函数y=2x图象的启示:通过对解析式y=2x进行简单的代数推理,学生猜出y=2x的图象,经历直观感受,列表时会聚焦坐标原点,向正负半轴取点,满足列表的需求;这些点分布在第一、第三象限,保证了描点的精确性;明确图象是一条直线,连线时可落笔出图.代数推理使得数学教学更具有流畅性,而教学的流畅性能使得学生具备良好的数学学习心理准备状态,从而更加轻松完成数学学习过程.此外,还可让学生自主完成k<0时猜图象的过程,实现代数推理对几何直观的辅助作用.

2.2 一次函数图象的教学——猜图象

已知一次函数解析为y=kx+b(k≠0),不妨设k>0,b>0,此时可取y=2x+3.

根据表2中的推理,猜出函数y=3x+3的图象如图2所示.

图2

表2 y=2x+3的简单代数推理

作函数y=2x+3图象的启示:通过对解析式y=2x+3进行简单的代数推理,学生猜出y=2x+3的图象,对其有了直观的认识.由代数推理猜出函数图象过两定点,不难发现(0,3)是一个整点,可以据此作为列表的基调;同时,函数经过第一、第二、第三象限,说明需要围绕点(0,3)向左和向右取点,列表水到渠成;两点、三象限限制落点的范围,函数图象大棋盘井然有序,接着顺次把点连,函数图象笔下生.对于水平较高的学生,依据一次函数图象可由正比例函数图象平移得到,明确其图象为一条直线,再结合两点确定一条直线,可直接得到一次函数图象.“经验重构”心理水平是后天学习活动的过程性结果,是长期“做数学”和“用数学”的经验缓存和补偿.从某种意义上来说,猜函数图象为这部分学生提供了经验重构系统,实现了经验重构,从而找到作一次函数图象的便捷方法;亦可改变k,b的正负,让学生自主完成知识的迁移,猜出其他类型一次函数的图象,进而更流畅地作出一次函数的图象.

2.3 反比例函数的教学——猜图象

表的简单代数推理

图3

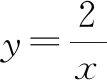
(1)函数图象在原点是间断的;

(2)列表分两步,可以先列x轴正半轴部分,再列负半轴部分;

(3)图象越来越接近x轴和y轴,说明函数图象是非均匀变化的,应为曲线而非折线;

(4)图象关于原点和直线y=x对称,使学生在描点和连线时更加流畅,同时水平稍高的学生可由第一象限的图象对称得到第三象限的函数图象.

由此可见,猜函数图象让学生由式想形,亦可迁移完成k<0时的代数推理,突破了对反比例函数图象的认知障碍,可高效完成反比例函数图象的绘制.

2.4 二次函数的教学——猜图象

初中数学二次函数图象的学习始于函数y=x2,在作函数图象之前,先对y=x2进行简单的推理.

根据表4中的推理,猜出函数y=x2的图象如图4所示.

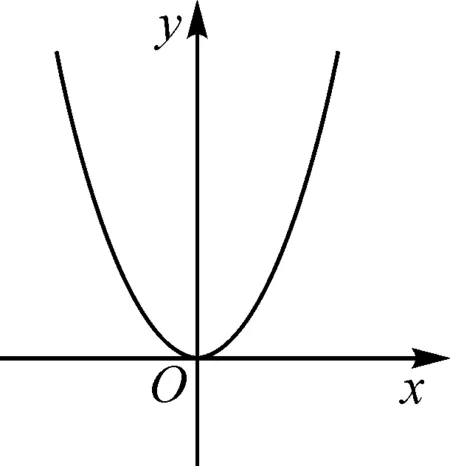
图4

表4 y=x2的简单代数推理

作函数y=x2图象的启示:对于刚接触二次函数的学生来说,二次函数是个函数与一元二次方程结合的“怪物”,猜函数的图象让学生提前窥探其真面目.经过对解析式y=x2进行简单的代数推理,学生猜出y=x2的图象,对其具有直观感受,提供简易作图支持系统:

(1)列表时聚焦坐标原点,向正负半轴取点,干净利落;

(2)点分布在第一、第三象限,描点心中有数;

(3)心中非均匀,笔下曲线连.y轴对称可取巧,先画半轴再翻折.

不难看出,猜出函数y=x2的图象,揭开了二次函数的神秘面纱,从而就能较为轻松作出二次函数的图象.结合平移知识,亦可让学生猜出函数y=ax2+bx+c(a>0)的图象,体现代数推理对于几何直观的辅助功能.

3 根据代数推理猜函数图象的过程

根据函数解析式进行代数推理猜函数图象的过程如图5所示.

图5

4 总结与反思

4.1 凸显解析式推理的魅力

根据解析式进行代数推理的魅力如图6所示.

图6

4.2 积累由数想形的基本活动经验

郭玉峰、张芳的研究表明,归纳概括、类比推广、数学表达、证明是数学基本活动经验的4个关键因素,是学生数学创新能力培养的关键.通过解析式的简单代数推理猜出函数图象这一过程蕴含归纳、数学表达的基本活动经验.在学习了正比例函数图象后,学生已经具备了归纳和数学表达的能力.而正比例函数、一次函数、反比例函数、二次函数属于同类知识,猜函数图象本质上是一致的,因此可以进行类比推广,提高学习效率,参见表5.

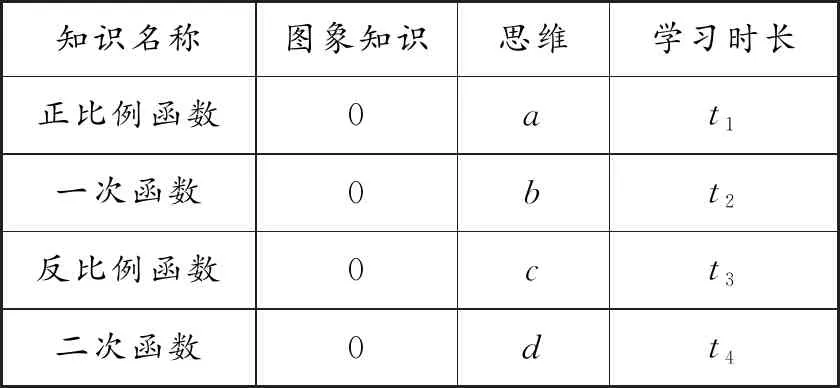
表5 猜函数图象情况一览表

从表5中不难发现,学习新函数时,学生对函数图象是陌生的,图象知识为0.同类知识学习过程中思维排序为at2>t3>t4,经验的积累、思维的提升使得学习的时长不断降低,契合大单元教学的模式和理念.

4.3 领会数形结合的基本数学思想

始于千古第一大定理——勾股定理,感悟几何与代数结合的美,至此数形结合不仅作为解决数学问题的工具,更被提炼成一种数学思想.函数可以视为数形结合的代名词,但仅仅把函数解析式与三部曲图象的联系视为数形结合远远不够,数形结合不是单行线,其过程是生生不息、循环往复的.如图6,通过代数推理,由数猜形,由推理结果确定列表、描点、连线的过程是由形写数,再通过三部曲作出函数图象是由数定形,最后通过函数图象验证函数解析式是由形验数.只有经历循环往复的数形转化才能从真正意义上领会数形结合思想,内化于心,外化于行.

4.4 把握函数内容的整体性

数学整体性教学的要求是:“数学知识的教学,要注重知识的‘生长点’与‘延伸点’,把每堂课教学的知识置于整体知识的体系中,注重知识的结构和体系,处理好局部知识与整体知识的关系,引导学生感受数学的整体性,体会对于某些数学知识可以从不同的角度加以分析、从不同层次进行理解.”根据函数解析式,进行简单的代数推理猜出函数图象这一过程,由数猜形,再由形验数,对于函数内容的学习具有普适性.从一次函数到反比例函数、二次函数,再到高中、大学学段的函数学习均有重要的作用,表明函数内容是一个有机整体,不可分割.每一类函数图象猜的过程核心都不变,但猜的结果不尽相同,正体现了知识的“生长点”与“延伸点”.因此,教师在教学中引导学生猜函数图象的活动,把握住了整体教学观,站在了教学的高起点,有助于学生建立良好的认知结构.