优化教学策略,实现高效复习

王 宏

⦿ 江苏省如皋初级中学

数学复习课是对阶段性知识的总结、巩固和强化,能够帮助学生加强对所学知识的理解,提升运用知识的技能,形成结构化的知识体系.既然数学复习课如此重要,就需要教师用整体性的眼光展开复习课教学,通过知识的综合化整理,激发学生的学习兴趣,弥补学习上的薄弱点,提高学习能力.本文中笔者从高效复习的角度出发,结合教学实践,谈一谈如何优化复习课的教学策略,以实现高效复习.

1 设计开放性练习,有效梳理知识

在复习课中,可以通过开放式的问题设计来调动学生的思维,促使学生在具体的问题情境中实现知识的再认和再现以及知识的有效梳理.

案例1“多边形”的复习课

问题剪去正方形的一个角,剩余部分还有几个角?

设计这样的练习目的在于调动学生已有的知识储备,激发学习的积极性,帮助学生在知识的回忆和再现中实现知识系统的初步建构[1].本案例中,教师通过开放性练习引导学生思考、操作、探索和交流,多方位、多角度去解决问题,最终在深度思考中个性化地完成对多边形知识的梳理.

2 选择典型试题,归纳解题方法

提升解题技能是数学教学的目标之一,在梳理基础知识之后,需要通过典型试题的练习让学生运用所学知识去解决具体问题,创新解题思路,归纳得出解题方法,最终达成高效复习的目标.

案例2“梯形”复习课的例题设计

问题如图1,梯形ABCD中,AD与BC平行,AB与CD相等,AD,BC,AB的长度分别等于2,8和6,求∠B的度数.

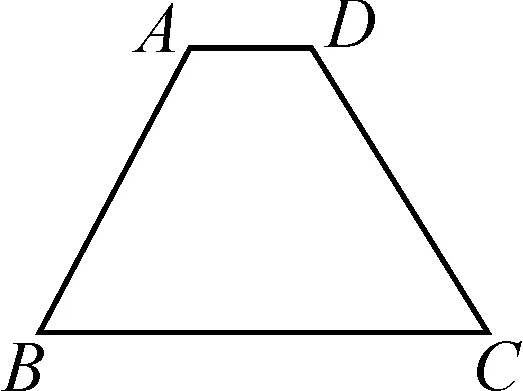
图1

在解决“梯形”的相关问题中,添加辅助线是一个难点,因此通过设计这一问题,帮助学生复习在梯形中添加常用辅助线的方法(见图2).

图2

本案例中的问题虽然并不复杂,而且是常规题型,但是可以引导学生回忆解决梯形相关问题中常用的几种辅助线,由此将梯形分割成特殊的四边形和三角形,从而找到解题思路.这样,通过典型试题,引导学生自主探索并归纳总结解题方法,在系统知识结构的基础上形成系统的解题策略,提升学习的有效性.

3 加强专题复习,总结解题规律

数学复习不仅要将零碎的知识进行总结和系统梳理,还要将分散的解题方法加以组织形成整体策略,从而更加便于在解题时灵活加以运用.因此,在教学中教师要加强专题复习以渗透总结和归纳知识点的方法,让学生去总结同类题型的解题规律,从而形成系统的解题策略,体会数学学习的价值.

案例3“圆的对称性”复习课

圆的知识常常在综合题中进行考查,难度较大,不少学生会因为思维不够严谨而束手无策或者出现漏解以及以偏概全的现象.基于此,笔者在“圆的对称性”复习课教学中就圆的问题设计了一组专项练习.

图3

问题2圆O的半径为5 cm,直径为AB,CD为弦,AB与CD垂直,垂足为E.设CD的长为6 cm,求AE的长.(学生分析题意,并作出图4.)

图4

变式1已知等腰三角形ABC内接于半径为5的圆O,设底边BC的长是6,求底角的正切值.

变式2已知圆O的半径为5 cm,梯形ABCD内接于圆O,AD和BC平行,AD的长度为6 cm,BC的长度为8 cm,求梯形ABCD的面积.

数学专题复习是进行知识提炼和总结的有效环节,能够系统化整理解题方法与规律,增强学生的学习信心,提升解题能力.本案例以题组的形式进行了圆的专题复习,通过设置不同的题目引导学生分类讨论,进而解决相应的角度、距离和面积问题,并总结与圆的对称性相关的解题规律.

4 利用错误资源,提升复习精准性

学生在练习中必然会发生一些错误,教师要关注学生的典型错误并进行整理,利用错误资源引导学生进行分析和思考,通过错误辨析,强化学生的认知,提升复习的精准性;还可以根据相关试题进行变式练习,从不同的角度进一步考查学生的知识掌握情况,帮助学生进一步巩固基础知识,深化对知识的理解.

案例4“三角形的高”的复习课

问题1如图5,过△ABC的顶点A,作BC边上的高,请将正确的选项填在括号内( ).

图5

本案例问题1的答案为选项A,其他选项虽然不正确,但是C,D选项中所作的垂线段同样也是△ABC的高.B选项中所作的垂线段CD不是△ABC的高,但是它也是垂线段.这样的非高垂线段虽然是错误选项,但是在解决一些几何问题中,却具有非常关键的作用.

问题2中∠EAF为45°,学生的第一直觉是过点E作EG与AF垂直,但是由于条件限制会遇到解题困难.不妨换一个思路,如图6,过点E作EG与EA垂直,由于∠EAF为45°,作非高垂线EG就成为了解题的关键.

图6

错误范例也是一种重要的教学资源,在学生的错误中蕴含着思维的过程和缺陷,孕育着正确的发现和创造因素.本案例中,教师利用错误资源,通过分析错误强化学生对关键知识的理解,拓宽解题的视野,进而提升数学核心素养.

5 加强变式训练,提升复习效率

变式训练是通过对原有问题的已知条件、设问方式、考查角度进行变化的方式,对学生进行强化训练,提升学生思维的灵活性和创新性.变式训练的方式有很多,如一题多变、一题多解、组合训练等,通过变式训练,能够培养学生从不同的角度灵活处理问题的思维能力,强化学生对知识的理解程度,提升学生对数学知识的认识.变式训练是一种有效提升复习效率的教学手段.

案例5二轮复习“探索性问题”变式练习设计

问题如图7,∠MAN的角平分线为AC,若∠MAN为120°,∠ABC和∠ADC都是直角,证明:AB+AD=AC.

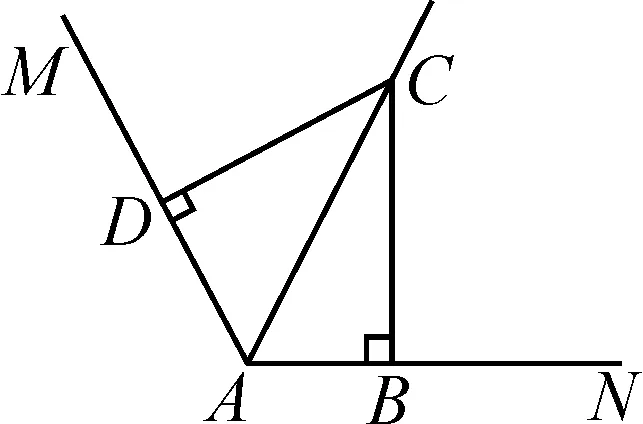
图7

变式1如图8,若∠MAN为120°,∠ABC与∠ADC的和为180°,请问以上问题中的结论还成立吗?若成立,请证明;若不成立,请说明理由.

图8

变式2如图9,①假设∠MAN等于60°,∠ABC与∠ADC的和为180°,那么AB+AD与AC的数量关系是什么?

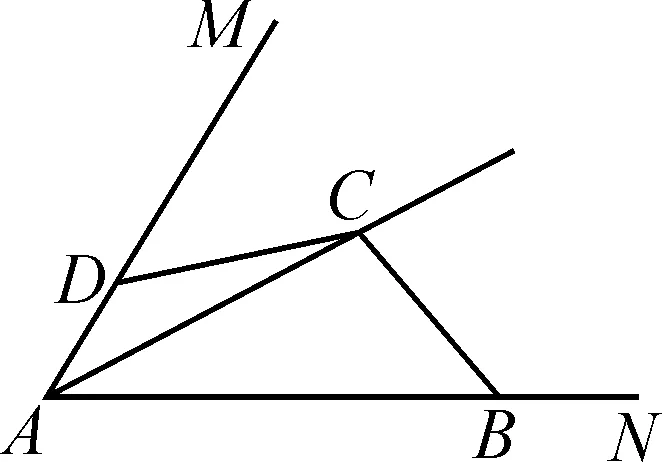
图9

②假设∠MAN=α,0°<α<180°,则AB+AD与AC的数量关系是什么?请用含有α的三角函数来表示并证明.

本案例中,通过变式练习,学生能够进一步把握知识之间的内在联系,从而在遇到题干条件发生变化时,能够有效地分析和思考,灵活运用所学知识解决问题,而不至于题目稍加变化就束手无策.这样的优质复习课堂,跳出了“题海”,避免了就题论题,以变式练习发展学生思维能力,提升了应变能力.

总之,有效的复习课能够强化学生对知识的理解,掌握数学的本质和规律,大大提升综合素养.教师要有效把握复习课的特点,优化复习策略,提高复习效率.教师要认真钻研,不断积累,多关注学生的发展需求,真正让学生在复习课中学会学习、学会复习,提升核心素养.