热载荷工况下的车轮裂纹周边应力分析及拓展评估

孙传喜,沈福,李航

(大连交通大学 机车车辆工程学院,辽宁 大连 116028)

轮轨关系直接影响着铁路运输的安全与稳定,国内外诸多学者针对该领域问题开展了大量研究,并取得了诸多成果。张野等[1]利用有限元法,研究瞬态热条件下车轮紧急制动时产生的热效应结果,考虑了车轮与闸瓦的热传导以及与空气的热交换,但未考虑在车轮内部既有裂纹情况下的热载荷影响。管建东[2]利用有限元法,研究热-机耦合作用下温度荷载对钢轨踏面裂纹扩展速率的影响。苏洪英等[3]为了研究贝氏体热轧钢轨踏面的裂纹扩展机理,进行了相应试验,研究表明控制适当合理的回火温度能够使裂纹的发展延缓并最终提高钢轨的使用寿命。戎有鑫[4]采用热-机耦合法讨论了滑动速度、轴重、环境温度等因素对轮轨表面温升的影响。刘洋等[5]建立了二维双线性弹塑性模型,将轮轨滑动接触处理成平面应变问题,分别研究了钢轨轨面剥落掉块和变摩擦系数对轮轨滑动接触热响应的影响。

本文从热载荷的角度出发,研究当车轮内部存在不同类型裂纹时,裂纹周边温度场及应力场的分布状态与变化规律。综合对比分析裂纹类型(直斜)、深度、位置(与表面接触区距离)等因素对于裂纹周边应力及裂纹拓展趋势的影响规律。

1 理论基础

1.1 热载荷有限元方法

本文基于更新拉格朗日描述方法,给出了应力场与温度场耦合的热弹塑性分析的增量有限元表示。

对体积为V,边界为S的连续介质,其能量守恒方程为:

(1)

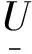
(2)

求解温度场时,塑性功转化成热量以焓的形式表示:

(3)

(4)

式中:M为功与热的转换系数。

1.2 断裂力学复合型裂纹的等效应力强度因子理论

鉴于轮轨接触问题的高度非线性特征,分析轮内裂纹应力强度因子时,不能简单地将其视为某一型裂纹,而应作为复合型裂纹考虑,因此对其裂尖应力场的描述采用等效应力强度因子。参考Brown[6]的三维复合型裂纹等效应力强度因子的计算式:

(5)

式中:β、γ为权重因子;KⅠ、KⅡ、KⅢ为Ⅰ型(张开型)、Ⅱ型(滑移型或平面内剪切型)、Ⅲ型(撕开型或平面外剪切型)应力强度因子。基于大量理论推导与试验验证[7-9],得出等效应力强度因子的计算式为:

(6)

2 轮轨弹塑性接触有限元模型

本文依据TB/T 449—2003中的相关参数,以JM型车轮与60 kg/m钢轨为研究对象,建立了大量瞬态热载荷轮轨弹塑性接触有限元模型。以裂纹长度为18 mm,深度为4 mm,角度为30°的模型为例,见图1。列车采用踏面制动时,车轮表层区域材料温度会高达400 ℃[10],将其作为热边界条件,在制动结束时施加于车轮表层材料。为了综合分析各项因素对裂纹周边应力场的影响规律,本文采用了控制变量法设置了多种计算工况,综合分析裂纹类型、深度、与表面距离等因素对裂纹周边应力场及温度场的影响规律。轮轨材料属性及计算热参数见表1。

表1 轮轨材料属性及计算参数表

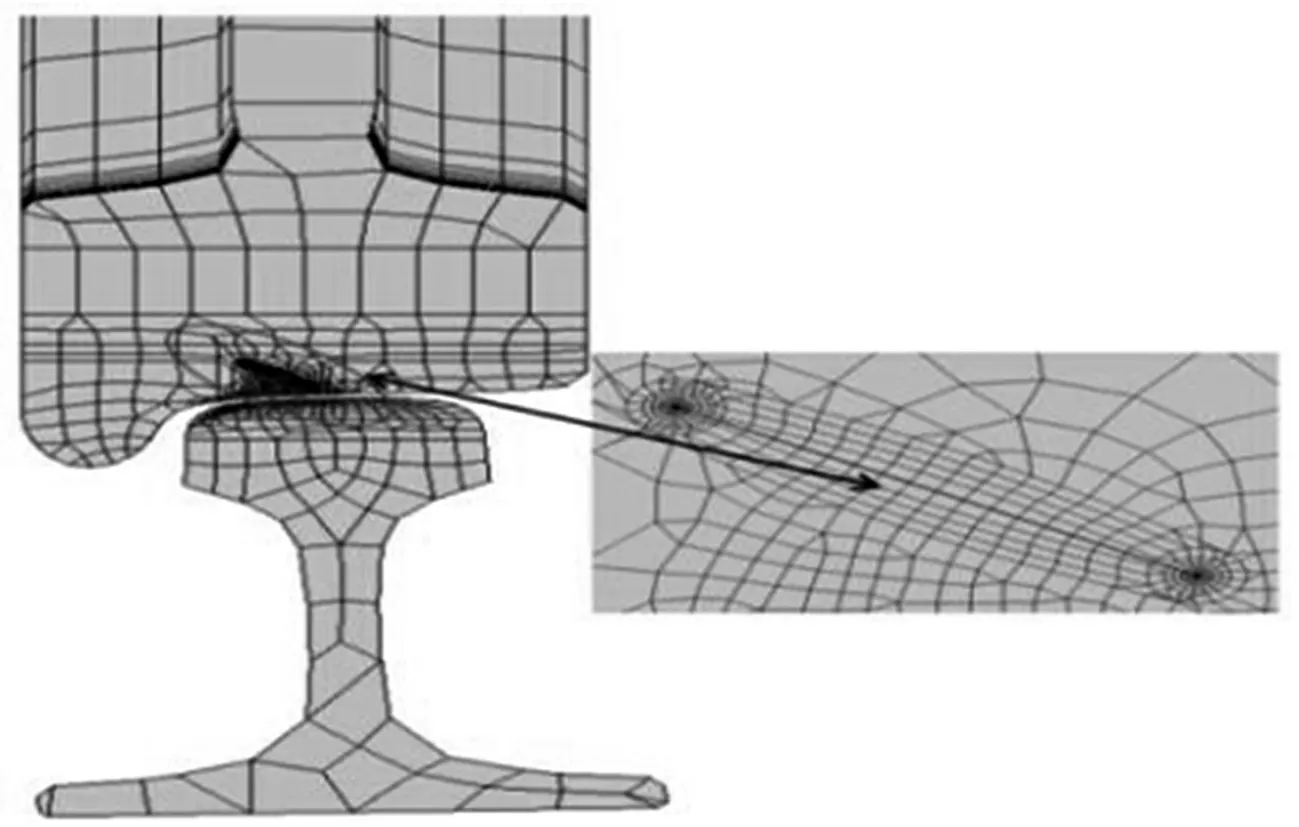
图1 有限元模型与裂纹局部

3 计算结果分析

本文基于各种工况计算结果,从多个角度综合分析了各种因素对裂纹周边应力场的影响规律。为了验证计算结果,本文同时利用虚拟裂纹闭合技术(VCCT),从应力强度因子的角度出发,验证计算结果的正确性,并对裂纹拓展速率及趋势进行判定。

3.1 裂纹周边应力场及强度因子分析

根据Hertz接触理论[11],轮轨接触最大等效应力区位于轮轨接触区次表层,即接触表面以下2～4 mm处。将裂纹设置于该范围内,以反映这一极端情况下的内部应力状态,从而使该研究更具有代表性与实际工程指导意义。由图2可知,随着裂纹深度的增加,裂尖周边最大应力也逐渐提高,对于直、斜两种类型的裂纹而言,均呈现此种规律,即裂纹深度的增加会加剧裂尖应力集中效应;各工况下,在大部分深度范围内,直裂纹裂尖应力场均高于斜裂纹。结合图3、图4可知,在轮轨瞬态接触传热过程中,裂尖周边5个特征节点的温度均迅速提高,其中温升最高的59 277号节点温升最高,在0.15 s内从0 ℃迅速增加到峰值145.5 ℃;随后随着热量向车轮内部材料传递,该节点温度又逐渐降低,在热应力场与纯机械应力场的叠加下,在温度达到峰值前,该节点的最大应力迅速提高至1 087 MPa,而纯机械载荷工况下该节点的应力最大值为871 MPa,可见,热应力对合成应力的贡献率高达24.8%,即热应力的影响不可忽略。

图2 裂尖应力随深度变化规律

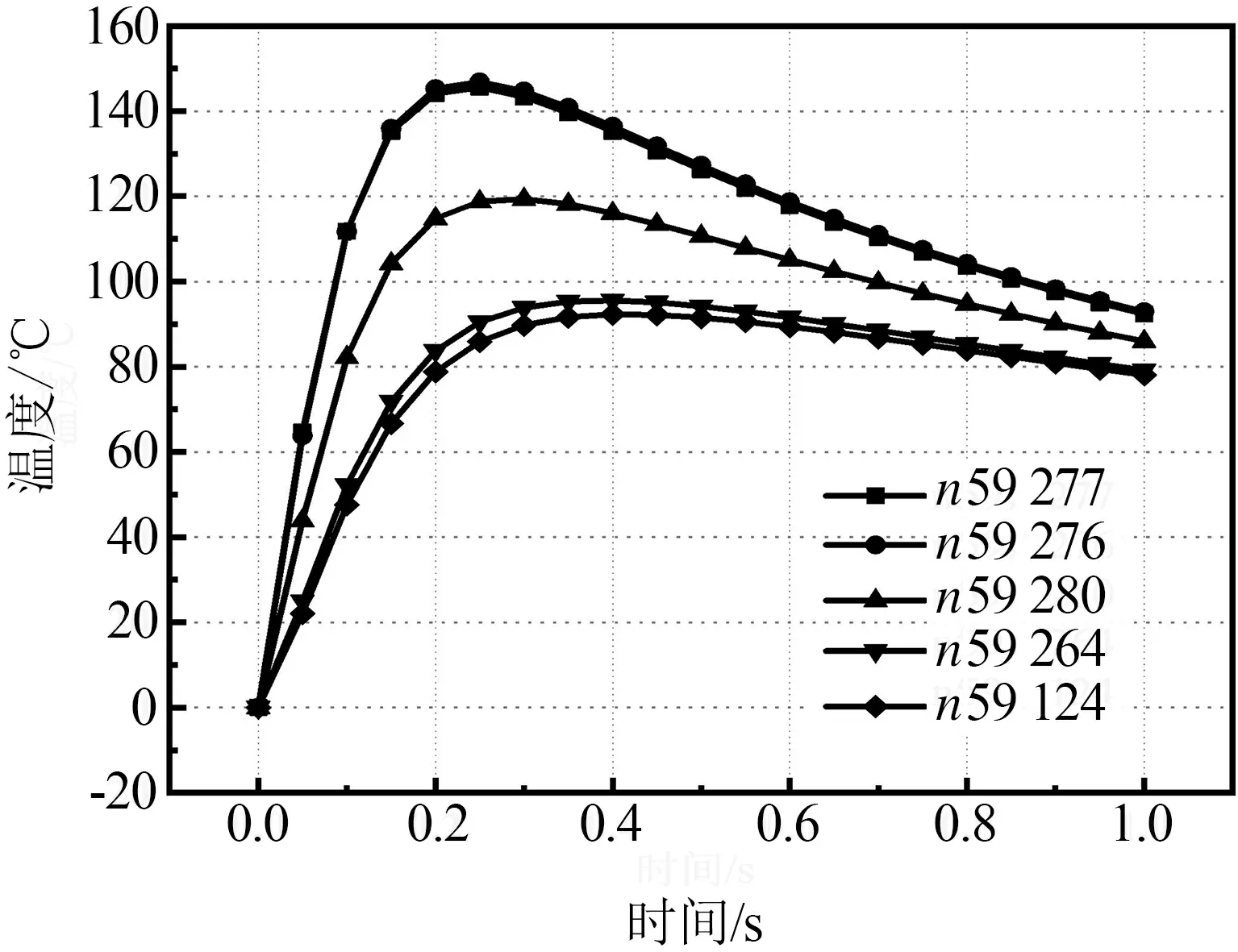
图3 裂纹周边不同节点温度随时间变化曲线

图4 裂尖应力采集点应力及温度变化历程曲线

本文基于虚拟裂纹闭合技术,求解了各工况下的裂尖应力强度因子,验证上述应力场分析结果,并判定裂纹的拓展速率及趋势。从图5、图6可知,随着裂纹深度的增加,在各工况下的KⅡ型应力强度因子逐渐增大,KⅢ型应力强度因子并非呈现规律性的单调形态。由于轮轨接触分析是复杂的非线性过程,因此在分析其内部裂纹裂尖应力强度因子时,不能简单地视为某一型裂纹,而应作为复合型裂纹考虑,在该载荷工况下计算裂尖的等效应力强度因子,得出其随裂纹深度的变化规律,见图7。叠加后的结果反映出复合型裂尖应力强度因子随裂纹深度的增加而逐渐增大,进而验证了裂纹深度对裂纹拓展速率及裂尖应力场的影响很大。相较该型材料的应力强度因子手册对应的门槛值KC(53 MPa),叠加后的应力强度因子最低为689.55 MPa,最高为1 495.11 MPa,显然已远超门槛值,即在此工况与此裂纹深度下,车轮内部裂纹会发生急剧拓展,甚至发生裂纹的二次拓展或出现多层裂纹,因此在检验过程中应重点关注裂深较大的裂纹。由图7可知,相较斜裂纹,直裂纹更易扩展,这验证了图2中直裂纹周边应力集中效应比斜裂纹严重的结论。

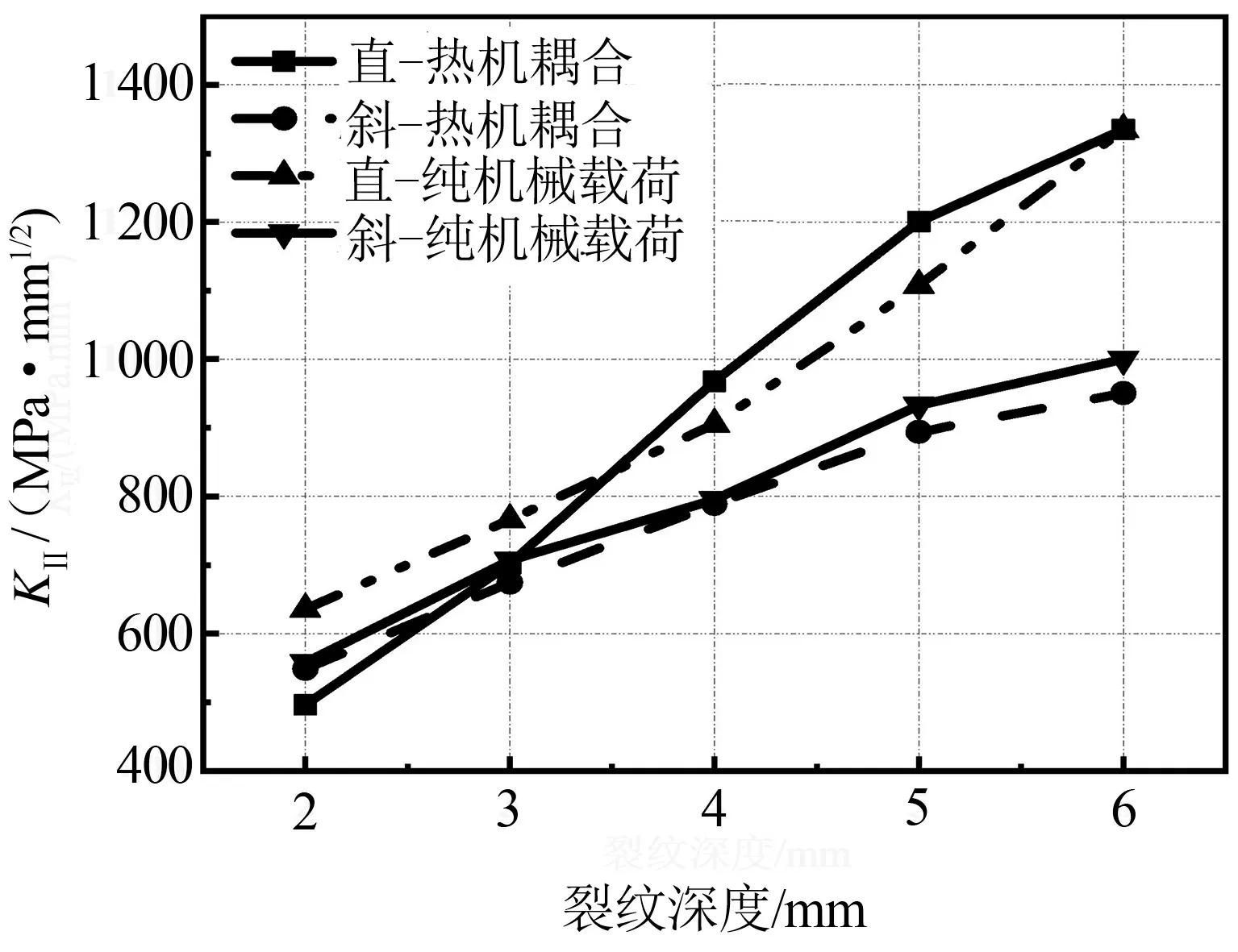
图5 KⅡ随裂纹深度变化规律

图6 KⅢ随裂纹深度变化规律

图7 Keq随裂纹深度变化规律

3.2 裂尖应力及强度因子分析

为反映车轮内部裂纹的多样性与随机性,本文在不同位置建立裂纹模型,以分析裂纹与车轮表面距离对裂纹周边温度场及应力场的影响规律。由图8可知,在同样的接触传热时间内,裂纹距离车轮表面越近,其周边区域温升越高;随着距离越远离接触区,其达到温度峰值的时间越长,同时热应力对轮内应力场影响较纯机械载荷越小。而对距离车轮表面较远的裂纹而言,热影响区尚未发展至该区域并产生显著影响,因而其温升相对较低。

图8 不同距离裂纹裂尖周边应力最大节点所对应的温度曲线

由图9可知,在各种工况下,裂纹周边最大应力点等效应力峰值均随裂纹与表面距离的增加而呈递减趋势,结合图8中温度场计算结果可知,裂纹距离表面越远,其温升越低,由其引发的热应力越低。

图9 各工况下裂尖应力最大值随裂纹与表面距离变化规律

KⅡ、KⅢ及复合型裂纹等效应力强度因子计算结果如图10～图12所示。随着裂纹与接触区的距离逐渐增加,KⅡ及KⅢ型应力强度因子均单调递减,其等效强度因子叠加结果也呈递减规律,验证了上述应力场分析结果。对距离接触区10 mm的裂纹而言,由于其在该工况下的等效应力强度因子值仍远大于材料的门槛值,该裂纹依然会拓展;同时可得出,裂纹位置越靠近车轮表面区域,裂纹强度因子越高,越易拓展并发展至表层,从而引起剥离掉块。

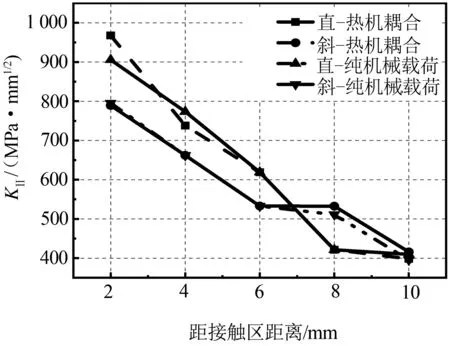
图10 KⅡ分布

图11 KⅢ分布

图12 Keq分布

4 结论

本文利用有限元法建立了车轮内部存在裂纹情况下的轮轨三维热载荷瞬态弹塑性接触计算模型,模拟踏面制动后的轮轨接触传热过程,并结合虚拟裂纹闭合技术验证应力场计算结果,同时分析了裂纹拓展趋势。综合对比分析各种工况下的计算结果,得出以下结论:

(1)某些工况下,热应力对裂纹处合成应力的贡献率可达24.8%,其对裂尖应力集中效应的影响不可忽略。

(2)各工况下,直裂纹裂尖应力场强度普遍高于斜裂纹,且应力强度因子值更高,该型裂纹更易拓展。

(3)裂纹位置越靠近车轮接触区表面,裂尖应力场及强度因子值越高,越易拓展,并发展至表层,从而引起剥离掉块。