一种环形交叉口“左转两步”信号控制的新方法

郭瑞军,高中传

(大连交通大学 交通运输工程学院,辽宁 大连 116028)

20世纪80年代,我国借鉴国外经验在城市中心建设了许多大型环形交叉口,在过去机动车保有量低的情况下,车辆能够有序驶出环岛。现如今机动车大量涌入环形交叉口,当车流量大于传统环形交叉口的调节能力时,则会导致整个环形交叉口出现“锁死”状况。针对环形交叉口拥堵问题,人们对环形交叉口的信号控制方式进行了研究,信号控制方式包括单重信号控制和双重信号控制。

单重信号控制方式大多采取对称式放行,并未完全分离冲突车流,对于此控制方式的研究主要集中在信号配时参数优化方面。为了分离不同冲突车流,避免环道内车辆冲突,杨晓光等[1]首次提出了大型四支路环形交叉口“左转两步”控制方法,并应用于厦门市莲坂环形交叉口,并取得了良好的效果。之后许多学者也对此控制方法的可行性与适用性进行了研究,并在此控制方法之上对相位衔接、相序、配时参数做出了诸多优化。Yang等[2],薛昆等[3]针对环型交叉口各流向的不对称性,以环形交叉口各流向饱和度均衡为优化目标,提出了基于非对称性的环形交叉口优化控制方法。马莹莹等[4]以十字环形交叉口内部各股车流的潜在冲突点和车辆启动形成的启动波为依据,给出了不同相位绿灯间隔时间的计算方法。刘泽[5]改进了“左转两步”控制方法,提出了各进口道轮流放行相位重叠方法,构建了相位重叠时间的计算模型,建立了环形交叉口高饱和交通状态下的周期时长优化模型并分析了其适用条件。Ma等[6]提出了一种基于双环方案的环形交叉口信号优化模型,考虑了周期长度最小化问题来生成环形交叉口的最优信号定时。Ma等[7]基于双环方案的环形交叉口信号优化模型,提出了能够同时确定信号环形交叉口车道标线和配时的综合优化模型,并通过案例验证了此模型具有很好的应用前景。管翔等[8]针对环形交叉口在非对称流量下的环道,利用不均衡问题进行了进口道流量优化,并提出了一种在流量差异的情况下,利用环道空间提前放行车流的方法。马新露等[9]提出了多进口协同放行的信号控制方法。也有学者从各股车流冲突、储存车道容量、每周期储存左转车辆数等方面给出了新的配时方法。刘灿齐[10]提出了一种基于冲突分析的环形交叉口信号周期计算方法。Chen等[11]提出了一种基于左转队列长度约束的环形交叉口信号配时方法。Murat等[12]提出了一种城市多车道“左转两步”控制环形交叉口的信号定时程序,加入了附加时间以及信号配时校准系数,利用迭代的计算方法求出最佳周期,并减少了车辆延误。此外,不少学者在环形交叉口通行能力[13-14]、储存车道[15]、交通排放及燃油消耗量[16]、储备通行能力和交织区域交通流特性[17-18]等方面也做了相关研究。本文为改善“左转两步”控制方式中左转车辆的通行效率,提高时空资源利用率,在避免各车流冲突的前提下,以四支路环形交叉口作为研究对象,对此控制方法的相位相序进行设计,分析环道二次左转车流运行特征,并结合实际左转车流给出了新的配时方法。为更精确地计算周期时长和环道绿灯时长,本文结合实际左转车流量以及运行特征,设计了相位相序图,给出了基于左转车流储存时长的配时方法,并分析了3种配时方法中各参数的计算原理。

1 环形交叉口“左转两步”控制简述

“左转两步”控制法需在进口道处及环道内设置左转专用车道,将左转车流单独分离出来,并分别受两次信号控制后,方可驶出环岛。即在进口道设置第一停车线、左转专用信号灯及直行专用信号灯;在环道各进口道左转车流与对向进口道左转车流冲突点前保持一定安全车距,设置第二停车线及专用左转信号灯,环形交叉口“左转两步”控制交通设计图,见图1。

图1 环形交叉口“左转两步”控制交通设计图

“左转两步”控制是为了避免各车流冲突,使左转车流有序驶出环岛。其中国内比较成熟的配时方法为杨晓光配时方法[1-3],国外配时方法为Cakici配时方法[12]。杨晓光配时方法注重二次左转车辆的释放,以此为依据来计算环道周期时长,并根据非对称流量对配时参数进行了优化,以下简称Yang方法。Cakici配时方法考虑到每周期进入储存车道的左转车辆数,根据实际情况,加入了附加时间及信号校准系数来优化配时参数,并利用迭代的思想求出总周期,以下简称Cakici方法。

Yang方法总周期根据每周期驶入环道左转车辆数迭代求出,根据进口道直行绿灯时长计算原理,会出现进口道左转绿灯时长较小的情况。Cakici方法周期值随流量改变,绿灯时长较大,会出现每周期驶入环道左转车辆超过储存车道容量的情况。两种方法都可能存在以下结果:环道二次左转车流较大时,二次左转车辆不能完全释放。

2 基于左转车流储存时长的配时方法

2.1 相位相序设计

在兼顾环形交叉口几何特征、时空资源利用、环道相位与进口道相位的衔接关系以及配时计算复杂程度的同时,采取对称放行的控制方式,针对四支路环形交叉口左转交通流量不对称的情况设计了基于NEMA相位的环形交叉口“左转两步”控制相位相序图,见图2。

图2 环形交叉口“左转两步”控制相位相序图

本相位相序图将环道相位和进口道相位结合在一起,且增加虚拟相位(相位1、3、5、7中的虚线箭头)确保上一相位的二次左转尾部车辆可以顺利通过本相位所对应的第二停车线,并顺利驶出环岛。虚拟相位的时长与二次左转车流量及储存车道长度有关。

2.2 配时方法

由相位相序可以看出,每个环道绿灯阶段均包含本进口道二次左转车辆的排出和下一进口道左转车辆的储存两个阶段,并且依次循环交替运行,以此为基础并结合实际左转车流量作为配时设计的总体思路。

一条左转储存车道的长度和车辆数为:

(1)

(2)

2.2.1 总周期时长

(3)

进口道i与进口道i+1对应环道信号灯灯色图见图3。

图3 进口道i与进口道i+1对应环道信号灯灯色图

(4)

式中:lj为相位损失时间,s。

由式(3)、式(4)可得出环道周期时长Cc,则环形交叉口总周期时长为:

C=max{Ce,Cc}

(5)

式中:C为环形交叉口总周期时长,s;Ce为进口道周期时长,s。

2.2.2 进口道直行绿灯时长

进口道i直行绿灯时长按照各相位直行最大关键流量比进行分配:

(6)

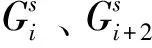
2.2.3 进口道左转绿灯时长

(7)

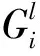
为确保进口道左转车辆顺利驶入环岛,需根据实际左转车流量分析是否与环道二次左转车辆存在冲突。

冲突判断如下:

(8)

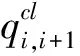
所以,进口道i+1左转绿灯相对于进口道i环道绿灯延启时间应满足:

(9)

存在冲突时,各绿灯延启时间示意图见图4,则进口道i+1左转绿灯相对于进口道i+1直行绿灯延启时间应满足:

图4 各绿灯延启时间示意图

(10)

最终,进口道i左转有效绿灯时长为:

(11)

2.2.4 环道绿灯时长

(12)

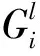
当二次左转车流较大时,进口道i所对应的环道二次左转绿灯时长需保证进口道i+1二次左转车辆顺利通过此信号灯排出环岛,环道绿灯时长优化示意图见图5,此时需增加虚拟相位确保二次左转车辆顺利驶出环岛。

图5 环道绿灯时长优化示意图

虚拟相位时长为:

(13)

则进口道i对应的环道有效绿灯时长为:

(14)

3 试验仿真

大连市数码广场环形交叉口位于沙河口区五一路与数码路的交会处,鸟瞰图见图6。其环岛直径为60 m,初始流量见表1,进口道与环道渠化为四车道,3种方法的配时图见图7～图9。为验证新配时方法的可行性及3种配时方法的适用性,将车均延误、平均最大排队长度作为评价指标,利用PTV VISSIM 9软件建模并在不同情景下对新方法、Yang方法、Cakici方法进行仿真,设计试验见表2。总流量增减试验以平峰流量作为初始流量(1.0倍),保持进口道各方向车流比例不变,改变总流量(0.7～2.0倍,以0.1倍递增);左转车流比例增加试验保持总流量不变,改变各进口道左转比例(-16%～+24%,以4%递增),增加或减少的左转流量平均分配给直行流量和右转流量;不同环形交叉口半径试验总流量同总流量增减试验,同时改变环形交叉口直径(80、100 m)。

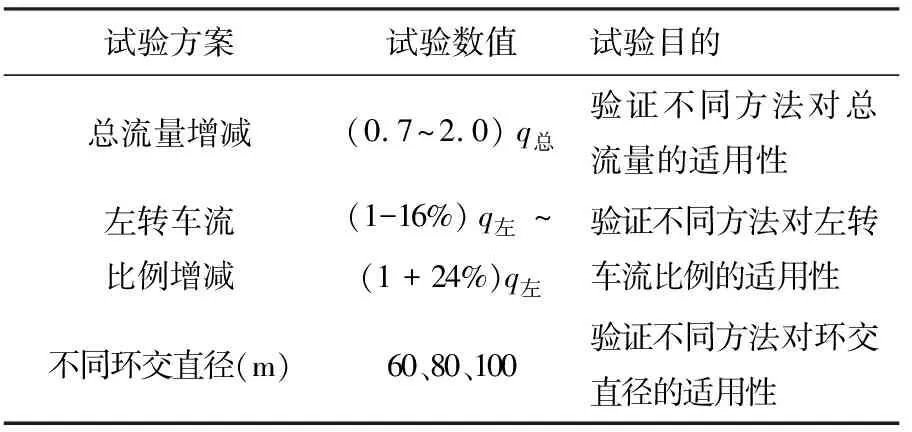
表2 试验设计

图6 大连市数码广场环形交叉口鸟瞰图

图7 新配时图

图8 Yang配时图

图9 Cakici配时图

3.1 总流量增减试验

3种配时方法的车均延误图见图10,平均最大排队长度图见图11。3种配时方法车均延误和平均最大排队长度总体上随着总流量增大而增大。新方法车均延误结果较好,Yang方法车均延误结果适中,Cakici方法车均延误最大。新方法和Yang方法第二停车线平均最大排队长度整体相近,Cakici方法第二停车线平均最大排队长度保持在约65 m且大于其他两种配时方法。3种配时方法的交叉口平均最大排队长度整体相近。

图10 总流量增减试验车均延误图

图11 总流量增减试验平均最大排队长度图

3.2 左转车流比例增减试验

车均延误图见图12,3种配时方法车均延误均随着左转比例的增大而增大。左转比例增减幅度为-16%～+8%时,新方法车均延误结果优于其他两种方法;左转比例增减幅度为+12%～+24%时,Yang方法车均延误结果较好。Cakici方法车均延误整体上大于其他两种配时方法。

图12 左转比例增减试验车均延误图

3.3 不同环形交叉口直径试验

不同环形交叉口直径车均延误图见图13。新方法和Yang方法车均延误随着环形交叉口直径的增大而增大,均在直径为100 m时,车均延误达到最大;Cakici方法随着直径的增大而减小,当直径为100 m时,车均延误达到最小。当直径为60 m时,新方法车均延误优于其他两种方法;当直径为80 m时,新方法与Cakici方法车均延误整体相近且优于Yang方法;当直径为100 m时,Cakici方法车均延误结果较好。

图13 不同环交直径车均延误图

3.4 仿真结果与适用性分析

试验仿真结果对比分析见表3,在直径较大的传统环形交叉口,本文基于左转车流储存时长的配时方法是可行的,且每种配时方法适用于不同的情景,可以根据不同的交通需求选取不同的配时方法。

表3 试验仿真结果分析

(1)总流量试验表明,新方法整体延误最小。总流量约为2 200～6 500 veh/h时,新方法车均延误相较于Yang方法减少约12%,相较于Cakici方法减少约20%。

(2)左转比例增减试验表明, 新方法适用于左转车流比例小于35%;Yang方法适用于左转车流比例约35%～50%。

(3)不同环形交叉口直径试验表明,新方法适用于环形交叉口直径小于80 m;Cakici方法适用于环形交叉口直径不小于80 m。

4 结论

(1)左转车流量是影响“左转两步”信号控制环形交叉口通行能力的重要因素之一,在配时过程中需着重考虑二次左转车辆的释放,避免出现环道“锁死”的情况。

(2)第二停车线平均最大排队长度可以作为环道拥挤程度的评价指标,其大于储存车道长度时,需重新优化配时参数。此外,左转车流比例可以作为不同配时方法左转车道划分的重要依据。

(3)本文配时方法是按照车辆到达符合平均分布来计算的,今后还需结合车辆到达分布函数,进一步精确计算配时参数。在一定程度上,新配时方法的设计思路可为环形交叉口感应信号控制提供一定的参考。