城轨列车多次制动作用下制动盘热-力耦合分析

张生芳,曹洋,尹剑,张勇阳,郝强,刘宇,程静

(1.大连交通大学 机械工程学院,辽宁 大连 116028;2.中国铁路郑州局郑州动车段,河南 郑州 450052)

制动盘在服役期间,每次制动都会产生大量的摩擦热,使制动盘的温度迅速升高。制动盘的散热受制动盘材料的导热率、制动盘与空气接触面积、空气流动速度等因素的影响,因此制动盘表面及盘体温度不能在短时间内冷却到室温。当两次制动间隔较短时,前一次制动在制动盘上残留温度和热应力等对后一次制动产生影响。周素霞等[1],张杰[2]对不同初速度下两次连续制动进行仿真分析,结果表明第二次制动的温度比第一次高,热量累积导致制动盘温度迅速升高。高温产生的热应力会导致制动盘出现裂纹和热斑[3]。耿凯[4]通过试验研究发现了制动盘损伤和制动过程温度的关系,温度越高,制动盘越容易发生损伤。针对研究制动盘的温度场和热应力场的研究,国内外学者采用了不同的方法,Modanloo等[5]采用分离变量法结合Duhamel积分法在柱坐标系下求解控制热传导方程,计算出初速度为350 km/h的均匀压力和均匀摩擦两种情况的温度数值。初明泽等[6]在充分考虑了制动闸片几何形状和分布对热流密度的影响后,建立了微元法的摩擦面热流密度计算模型。在制动时,制动盘的温度分布受到很多因素的影响。陈昶等[7]利用单因子变量法,研究不同制动盘结构对温度和应力的影响,结果表明,夹层式结构通风孔制动盘的总体性能更好。Yang等[8]考虑了变摩擦因素的影响,提出了一种新的计算制动盘温度场的模型,对比实验发现在没考虑变摩擦因素时最高温度被低估了15%。为了降低制动盘的温度,Jian等[9]在制动盘中装上热管,将制动盘高温区的热量向低温区转移,很好地降低了制动盘的热量。总结以上文献可以发现,针对盘式制动器制动过程的研究目前多为制动盘的单次制动工况,然而,制动盘在实际服役期间多次制动的情况频繁发生,且前一次制动会对后一次产生影响。

本文针对制动盘多次制动作用下热-力耦合规律进行研究。利用有限元仿真软件,建立了多次制动作用下制动盘热-力耦合有限元仿真模型,得到了多次制动过程中温度场和应力场的变化云图。通过对多次制动温度和应力变化规律的分析,得到了前一次残余温度对后一次制动的影响机制。

1 多次制动仿真模型建立

1.1 城轨列车多次制动工况

本文以某列车的运行工况为例,对制动盘多次制动工况进行讨论。由文献[10]可知,列车进站后停留的时间为30 s,随后列车开始启动,列车的启动时间为35 s。在下一站进站前开始制动,假设列车制动完全依靠盘式制动器,制动时的减速度为1.06 m/s2,则列车的制动时间为21 s[11],此时制动盘处于制动状态,列车在站内停留和行驶过程中制动盘都此处于冷却状态,制动盘处于冷却状态的最短时长为120 s[10]。列车运行过程中制动盘的工作状态见表1。为研究多次制动作用下制动盘热-力耦合规律,做出如下假设工况:

表1 列车运行过程中制动盘工作状态

(1)制动盘每次制动时间相同,为21 s。

(2)相邻两次制动的冷却时间相同,为120 s。

(3)制动盘进行连续5次制动。

1.2 有限元仿真模型建立

本文建立多次制动作用下制动盘热-力耦合有限元仿真模型,做出如下假设:

(1)在同一圆周方向上,制动盘与闸片摩擦面的压力处处相等。

(2)忽略在紧急制动过程中制动盘与闸片的磨损,认为制动过程中的动能全部转化为内能,并且按照一定的热流比例分配到制动盘与闸片上面,同时忽略热辐射散发的热量。

(3)制动速度由初始值线性减小到0。

(4)制动过程中环境温度为20℃保持不变。

(5)制动盘简化为各向同性材料。

制动盘外径R=320 mm,内径r=150 mm;制动盘为带有散热筋结构,散热筋尺寸为105 mm×20 mm×30 mm。两摩擦面关于中间面对称,为方便计算取制动盘厚度的一半进行分析,建立制动盘/闸片有限元模型见图1。在定义约束过程中,约束制动盘x、y、z方向的移动副和绕x、y轴的旋转副,只保留绕z轴的旋转副;约束闸片x、y方向的移动副和绕x、y、z方向的旋转副,只保留沿z方向的移动副,同时在闸片表面施加20 000 N的制动压力。制动初始速度为80 km/h,初始温度为20 ℃,摩擦半径为275 mm,仿真制动时间为21 s,冷却时间为120 s,循环5次,总时间为705 s。

图1 制动盘/闸片有限元模型

制动闸片的材料为铜基粉末冶金,材料属性如下:密度为5 500 kg/m3;热导率为30 W/(m·℃);比热容为550 J/(kg·℃);线弹性模量为5.2×109Pa; 线性膨胀为1.5×10-5℃-1; 泊松比为0.3;制动盘的材料采用Q345B,制动盘材料变化参数见表2;制动界面摩擦系数见表3。

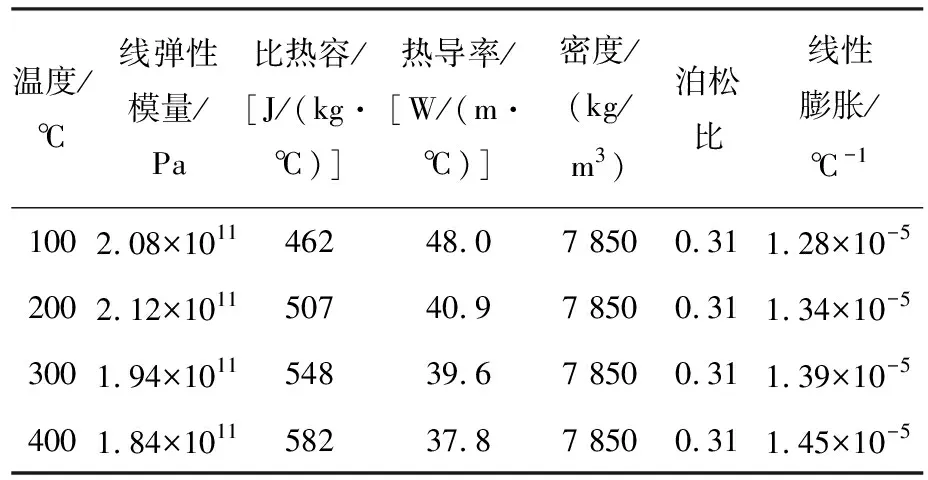
表2 制动盘材料变化参数

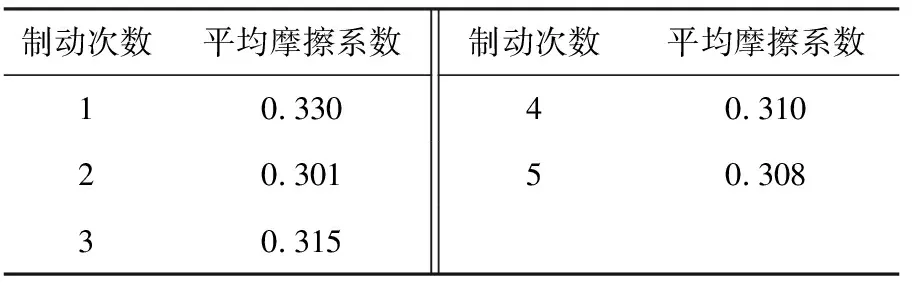
表3 制动盘与闸片摩擦界面摩擦系数变化

1.3 热传导

制动盘三维瞬态热有限元分析中热传导方程为[12]:

(1)

式中:ρ为材料密度;cT为材料比热容;kx、ky、kz为节点沿x,y,z三个方向的导热率;Q为研究对象的自身热源强度。

1.4 对流换热

制动过程中制动盘的换热过程以对流换热为主,则对流换热系数的经验计算公式为[13]:

(2)

Re=ωρaD2/(2ua)

(3)

式中:ka为空气的导热系数;D为制动盘的外直径;Re为空气的雷诺数;ρa为空气的密度;ua空气的动力黏度;ω为制动盘转速。

2 热-力耦合有限元仿真结果分析

2.1 多次制动过程中温度变化分析

制动过程中产热散热机制十分复杂。下文对第1次制动过程中制动盘的温度变化进行分析。第1次制动不同时刻温度云图见图2。从图2可以看出,摩擦区域温度在制动盘表面呈环形分布,定义此处为环状高温区。制动1 s时靠近制动盘摩擦外径的温度达到42.16 ℃。当制动时间为15 s时,最高温度升高到298.00 ℃,制动结束时最高温度下降到226.90 ℃。制动盘最高温度呈现先上升再下降的趋势,这主要是由于沿制动盘径向摩擦中心处,制动盘与闸片持续摩擦,热量不断堆积,使得摩擦区域的温度不断增加。由于热传导的作用,摩擦产生的热量可以向非摩擦区域传递,沿径向靠近摩擦边缘区域的温度上升远小于中心区域,造成环状高温区域宽度比制动开始时变窄。冷却结束后,制动盘径向方向上依然存在高低温度差。在制动盘上存在温度相对较高区域,此处为制动盘与闸片接触区域,由于闸片的存在使周围空气温度较高,减弱了制动盘与空气的对流换热,使此处温度下降慢。由图2(d)可知,制动盘前次制动尚未冷却到常温时即开始执行第2次制动。

图2 第1次制动不同时刻温度云图

制动盘制动5 s后的温度云图见图3。从图3可以看出,制动盘的温度随着制动次数的增加逐渐增高,制动表面环状高温区域与低温区分界线越来越明显,最高温度逐渐升高。同时制动盘的最低温度也逐渐升高,由第1次制动的20.00 ℃升高到第5次制动38.17 ℃,这种现象主要是制动盘上残余温度所致。残余温度使制动盘的初始温度升高,制动过程的最高温度就会相应提高。相邻两次制动的残余温度上升幅度很小,就会造成后期制动最高温度上升幅度小。

(a)第1次

制动盘表面温度沿径向呈现低温-高温-低温的趋势。为深入研究多次制动温度变化规律,分别在沿径向的高温和低温区选择典型节点提取温度数据,绘制温度变化曲线,见图4。制动盘半径246.08 mm处升高到最大值,此时制动盘与闸片摩擦产生的热量与制动盘向外界散发的热量相同。随后制动盘产热量小于散热量,则制动盘表面温度开始降低。当时间为21 s制动结束时,盘式制动器进行冷却,制动盘与闸片分离,此时制动盘不产热只散热。当温度降到100 ℃以下时,制动盘对流换热系数减小,温度下降缓慢。在时间为141 s时第2次制动开始,此时制动盘尚未冷却到室温,制动盘存在热量累积,使得第2次制动的最高温度大于第1次制动的最高温度。随着制动次数的增加,相邻两次制动时的最高温度差值越来越小,前一次制动对后一次制动的影响越来越弱,制动盘的最高温度逐渐趋向390 ℃。在制动盘半径171.26 mm和299.13 mm处为非摩擦区域,不存在摩擦生热的现象,则非接触区域的热量通过热传导的方式获得。当摩擦区域温度较高时,非摩擦区域温度升高得快;当高温区温度下降缓慢,则向外传递的热量也有所减少,此时非摩擦区域的温度上升得慢。由于制动盘半径171.26 mm和299.13 mm处与高温处的距离不同,所以温度上升的趋势也有所差异。

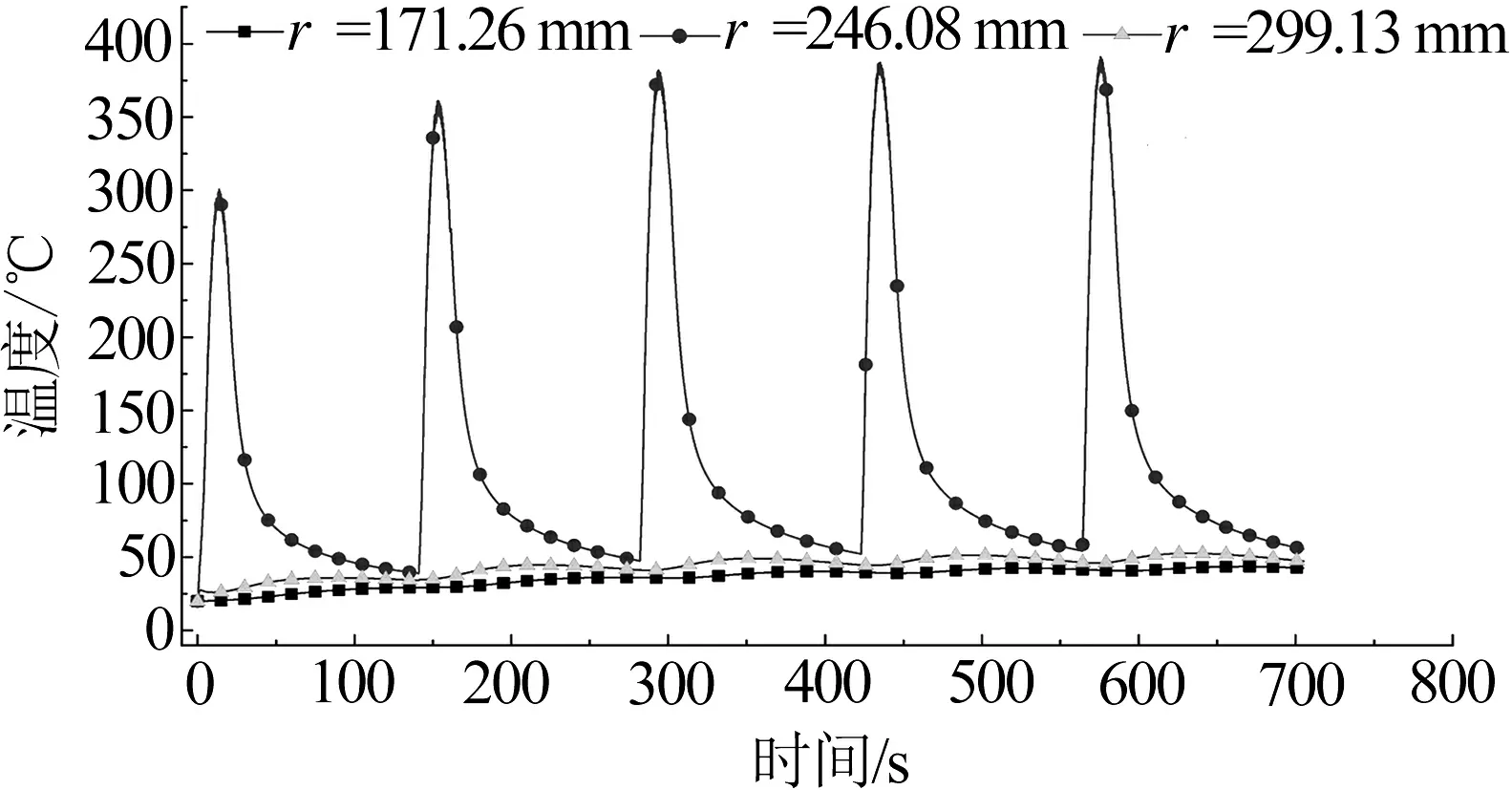
图4 不同半径处温度曲线

2.2 多次制动过程中应力变化分析

当物体温度改变时,由于外在约束和物体内部之间相互约束,使其不能完全自由胀缩而产生的应力叫做热应力。制动盘表面温度变化产生的应力云图见图5。从图5可以看出,由温度产生的应力在摩擦区域也在制动盘上呈现环状。对比图2可以发现,温度高的位置应力大。制动盘存在散热筋,散热筋有减小制动盘内应力的作用,最大应力发生在没有散热筋支撑部分,沿圆周方向呈点状均匀分布。随着制动的进行,制动盘温度升高,热应力增大;随着制动时间的增加,制动盘的最大应力逐渐往半径的中心区域移动。当制动盘冷却一段时间后,应力分布发生明显变化,最大应力发生在制动盘半径最小部分,沿着半径方向大致呈现由高到低的分布,外径处应力最小。这是由于制动盘的内径与车轴连接,在连接处阻碍了制动盘的热胀冷缩,导致其应力增大。

(a) 制动1 s

在前次制动完成后,制动盘还存在着残余热应力便开始下次制动,盘中残余热应力将会对下次制动产生影响(图6)。对比第1次和第2次制动5 s后的云图可以发现,由于制动盘上的温度和残余应力的影响,盘表面的应力逐渐增大。随着制动次数的增加,最大应力区宽度相比第一次制动时变窄。制动盘径向靠近中心的区域由于与车轴固定,此处的应力随着制动次数增多而加大,制动盘内径处产生的应力最大值为83.44 MPa。

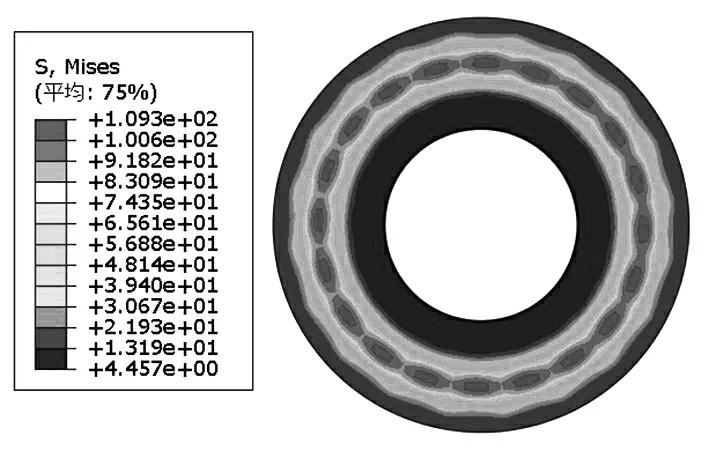
(a)第1次

为研究应力随时间的变化规律,沿径向方向在最大应力区及其两侧分别取一个点,提取应力数据,绘制应力随时间的变化曲线,见图7。制动盘的应力与温度相关,分析时参考图4。半径在246.08 mm处为制动盘的摩擦区域,制动开始时由于制动盘表面的温度迅速升高,制动盘的热应力迅速增大。当制动盘的温度到达最大值时,制动盘的热应力同时达到最大值,为231.26 MPa。随着制动次数的增加,最大应力也逐渐增加,但相邻两次制动的最大温度差值越来越小,导致相邻两次制动的最大应力差值越来越小,逐渐趋向300 MPa。温度降低,应力随之减小;制动盘应力变化趋势与温度变化趋势相同。半径为298.75 mm处在单次制动中,应力先快速上升然后再急速下降,最后稳定在某一数值。而半径为171.90 mm处,随着摩擦区域的应力增大而增大,在最大应力下降后,此处的应力下降非常缓慢。这主要因为在半径298.75 mm处,温度是制动盘应力的主要影响因素,而半径171.90 mm处除了温度影响制动盘的应力,制动盘与轴的固定连接也在阻止盘体的热胀冷缩,因此此处的应力较大。

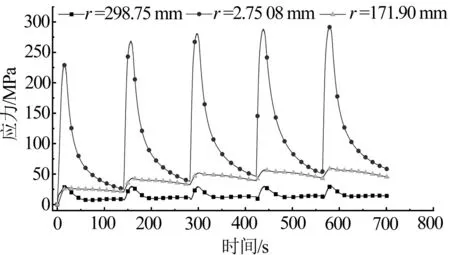
图7 多次制动应力曲线

2.3 散热筋的温度和应力变化分析

为研究制动盘散热筋的温度、应力情况,在散热筋上均匀选取6个点,观察温度和应力变化情况,见图8。

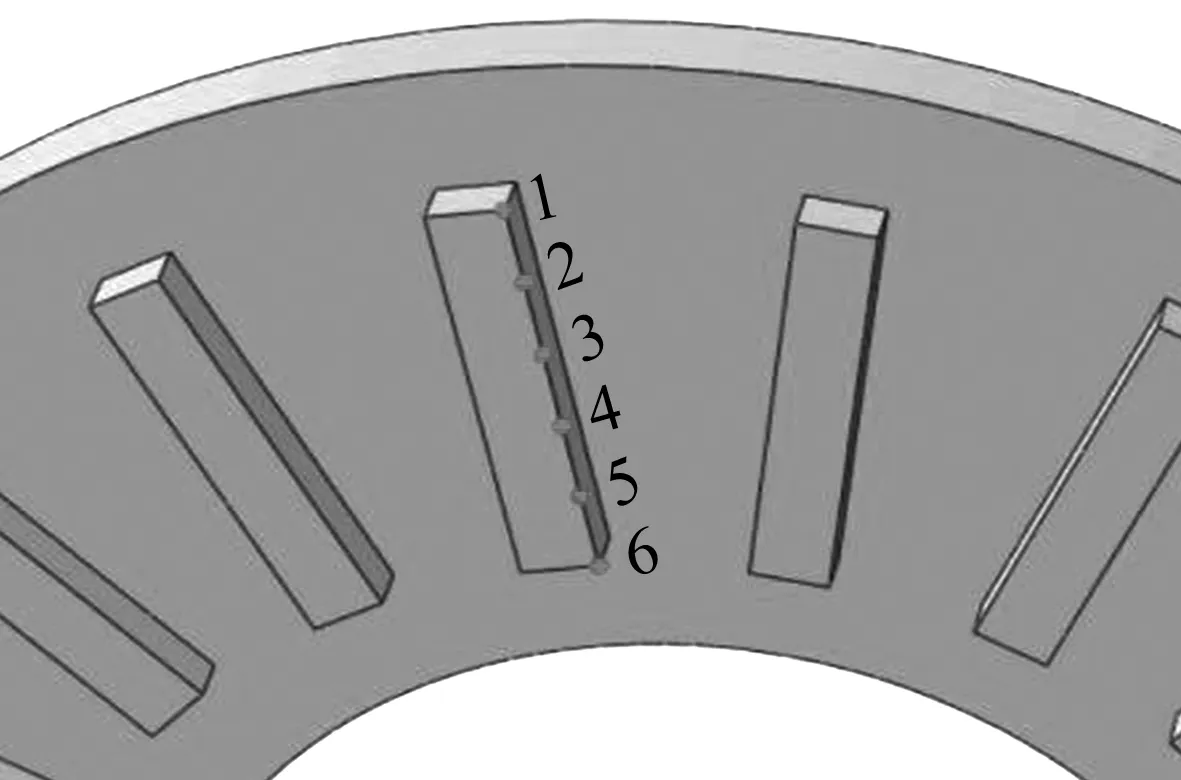
图8 散热筋分析点

散热筋不同位置的温度变化情况见图9。从图9可以看出,点3位置的温度最高,沿制动盘径向向两侧温度逐渐降低。造成这种现象的原因是点3靠近制动盘的高温带,传导到此处的热量较多,温度较高。散热筋各点的温度每次制动时都不相同,随着制动次数的增加,制动盘散热筋的温度逐渐升高。在制动盘处于冷却状态时,由于冷却时间较短,制动盘并不能完全冷却,造成每次制动时制动盘的初始温度升高,制动盘的整体温度也随之上升,散热筋的温度也会相应升高。

图9 散热筋不同位置温度变化情况

散热筋不同位置应力变化情况见图10。从图10可以看出点3为应力最大的点,沿制动盘径向向两侧散热筋的应力逐渐减小。这主要由于点3靠近制动盘的温度和应力最大值的点,受制动盘温度和应力的影响,点3为应力最大点。每次制动时散热筋各点的应力不同,随着制动次数的增加,散热筋的应力逐渐增大。温度是产生应力的主要原因,当温度增加时,散热筋的应力增大。由图9可知,每次制动散热筋的温度逐渐升高,应力也随着增大。点6在每次冷却后的应力值大于点5,其原因是点6靠近制动盘与车轴连接部位,受连接影响此点应力大于点5。

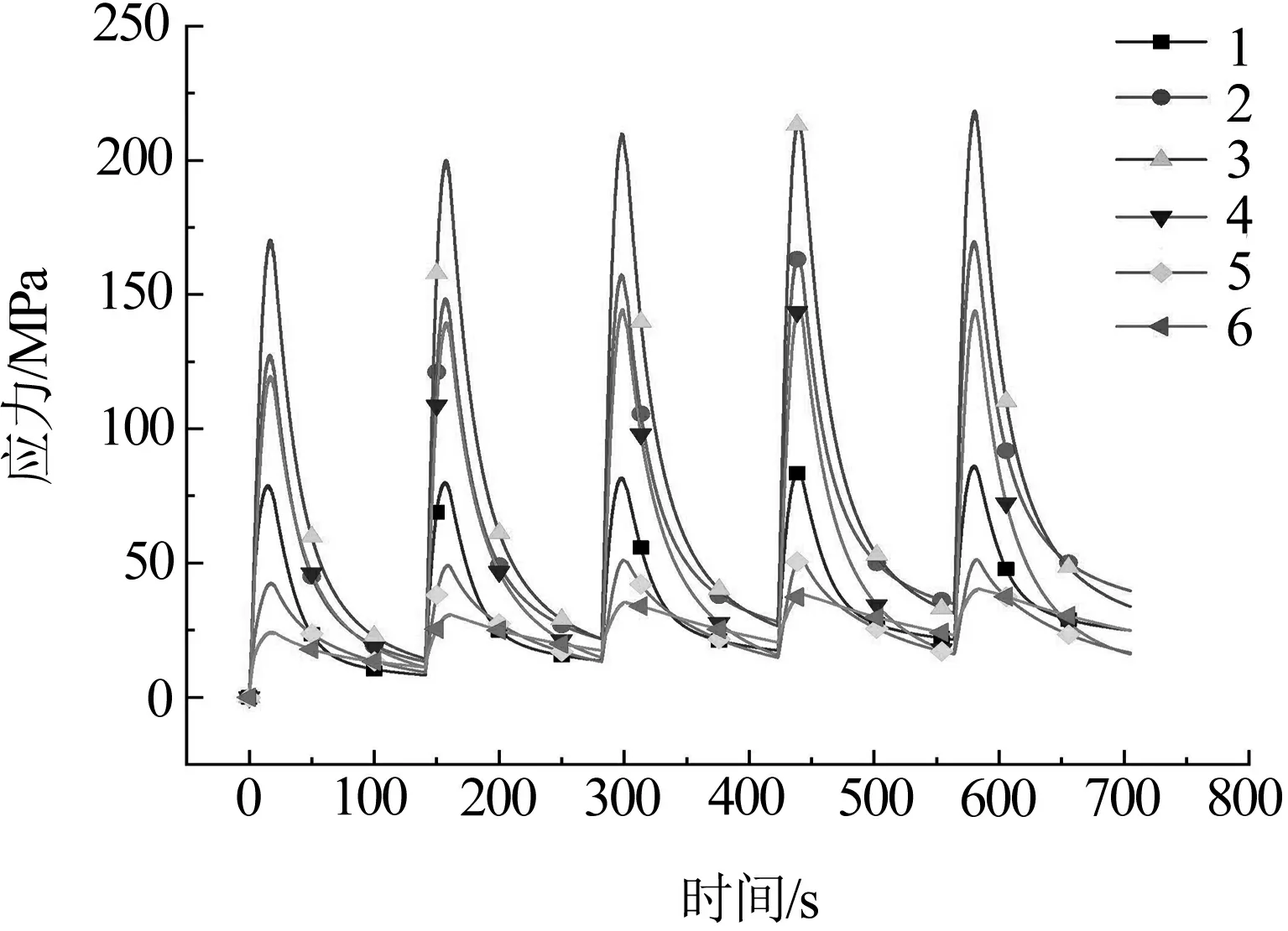
图10 散热筋不同位置应力变化情况

3 结论

本文根据列车的运行工况,建立了多次制动作用下制动盘的热-力耦合有限元仿真模型,得到了制动盘温度、应力沿径向和随时间变化的规律。分析了在多次制动过程中前次制动产生的残余温度、残余应力等对后续制动的影响。具体结论如下:

(1)制动盘的温度在单次制动过程中呈现环状分布,沿径向方向呈先升高后降低的趋势,最高温度区域发生在沿半径方向的中间区域。随制动次数的增加最高温度也逐渐升高,最后趋向390 ℃。

(2)制动盘的应力在单次制动过程中同样呈现环状分布,沿径向呈现先增大再降低的趋势,最大应力发生在沿半径方向的中间区域。由于散热筋的存在,最大应力沿圆周方向呈现点状分布。随制动次数的增加最大应力也逐渐增大,最后趋向300 MPa。

(3)多次制动过程中前次制动残余温度主要影响制动盘温度大小,对温度分布规律没有明显影响;前次制动的残余温度和残余应力不仅使后次制动的应力变大,还使得靠近制动盘内径处应力不断提高。

(4)制动盘散热筋的温度和应力随制动次数的增加而升高,应力随制动次数的增加而增大,散热筋靠近制动盘高温带的部分会产生高温和高应力。