基于鲸鱼优化的疲劳驾驶识别方法研究

李作进,史蓝洋,冯世霖,陈智能,曹亚男,贺学乐,陈生富

(重庆科技学院 电气工程学院,重庆 400000)

随着我国经济发展,汽车保有量已达到3.3亿辆[1-2]。汽车数量的迅速增长使得道路交通事故发生数量逐年攀升,其中超过20%的交通事故是疲劳驾驶所致,疲劳驾驶已成为道路交通事故的头号杀手[3-4]。驾驶员处于疲劳状态时,对车辆的控制水平以及自身生理机能、辨识能力都在下降[5]。如果可以实时监测驾驶员状态,对已处于疲劳状态的驾驶员警示,就可以避免部分道路交通事故的发生。

当前疲劳驾驶检测主要分为接触式和非接触式两种。接触式检测主要是通过驾驶员的生理信号变化情况,如脑电信号[6-9]、心电信号[10-11]、脉搏波信号[12]等对驾驶员所处状态进行分析,但这种检测方式属于入侵式检测,驾驶员穿戴的电极式数据采集装置会影响到自身的操作,出于安全考虑等原因,大部分研究工作者还是偏向于非接触式的检测方式。非接触式检测根据检测目标的不同在车辆相应位置安装数据采集装置,不会影响驾驶员的操作亦不受环境变化的影响,其结果稳定性是最高的,且成本低,适合面向实际,已成为如今疲劳驾驶检测方法的研究热点[13-15]。

以驾驶操作行为为研究对象的疲劳驾驶检测属于非接触式检测。张希波等[16]提取方向盘的转角零数百分比和角度标准差,采用Fisher线性判别方法对疲劳状态进行识别,其试验结果的准确率达到82%。Li等[17]采取滑动时间窗对方向盘转角时间序列提取近似熵(ApEn)特征后利用二元决策分类器对驾驶员疲劳状态进行辨识,在实车数据下的检测准确率达到78.01%。然而现有文献以单一特征比如方向盘转角的居多,涉及多种特征信息融合的少。准确率能达到80%以上的多是在虚拟驾驶环境下采集的数据,缺乏在实车路况下的有效验证[18-22]。

基于此,本文对实车路况下的驾驶操作行为展开研究,从方向盘转角、车速、横摆角速度、车辆横向加速度中抽取表征疲劳水平的统计类特征指标,通过单因素方差分析筛选指标,采用鲸鱼-决策树算法(WOA-CART)搭建疲劳驾驶检测模型,以实现对驾驶员疲劳状态的监测和预警。

1 驾驶操作行为特征提取与筛选

1.1 操作行为统计特征提取

张希波等[16]在研究中发现,驾驶员疲劳状态一般会持续15～75 s,但相应驾驶操作行为的变化只会出现1～2次,每次的持续时间一般为5～20 s。因此,为了避免特征削弱,本文采用双时间窗方法。如图1所示,其中样本窗T为60 s,时间窗t在样本窗上以步长l s滑动,计算每一时刻时间窗ti=6,11,16(i=1,2,3)内的驾驶操作行为变量值,取其最大值作为样本窗T内的指标值。

图1 双时间窗示意图

所提取的驾驶行为统计指标见图2。分别就车速、方向盘转角等4种操作行为,通过双时间窗方法提取峰峰值、绝对值均值等6个有量纲统计特征和峰度、变异系数等3个无量纲统计特征以及频数百分比[19]这一经验类特征,随后将对这些所提取的特征进行筛选,组成一个最优特征输入集。

图2 驾驶行为统计特征提取指标

部分公式如下:

(1) 绝对值均值:

(1)

式中:M为绝对值均值;n为三级疲劳样本的个数;θ为样本时间序列值。

(2) 标准差:

(2)

式中:Std为标准差,其值为方差的算术平方根,主要反映一个样本数据集的离散程度。

1.2 最优特征筛选

单因素方差分析[20]是检验各因素对试验指标是否存在显著差异的一种统计方法,可以有效对驾驶行为指标进行筛选,去除冗余指标,提高分类模型的性能,减少模型搭建时间。其影响因子水平为驾驶员清醒、疲劳和非常疲劳三种状态。基本思想就是用组间偏差平方和SA和组内偏差平方和Se的大小来衡量影响因子的影响效果。

检验的零设公式为:

H0:μ1=μ2=μ3=μ

(3)

式中:μ1为清醒状态下总体期望;μ2为疲劳状态下总体期望;μ3为非常疲劳下总体期望;μ4是所有总体的均值。

(4)

(5)

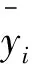
ST=SA+Se

(6)

引入均方和排除自由度不同所产生的干扰,定义F统计量来检验H0,即:

F=MSA/MSe=(SA/fA)/(Se/fe)

(7)

式中:MSA为组间均方和;MSe为组内均方和;fA和fe为自由度。给定显著水平α,H0的拒绝域为:

W={F≥F1-α(fA,fe)}

(8)

若拒绝域成立,则可以认为所选的疲劳特征指标对三级疲劳水平有显著影响。

2 疲劳水平的鲸鱼-决策树识别

2.1 CART算法

本文采用决策树类别中使用基尼系数生成分类树的CART(Classification And Regression Tree)算法。构造CART分类树的过程是根据数据特征将数据集分类的递归过程,有特征选择、决策树生成和剪枝3个部分。如图3,将疲劳样本数据集放到根节点中,根据基尼系数从数据集各个疲劳特征中选择一个特征作为当前节点的分裂标准,从上至下递归生成内部节点,直到所有训练数据集被基本正确分类,生成二叉决策树。叶节点即为分类标签。剪枝则是由于决策树容易过拟合,通过缩小树结构规模来予以缓解,以实现更好的泛化能力。

图3 决策树结构图

2.2 鲸鱼优化算法

鲸鱼优化算法(Whale Optimization Algorithm,WOA)是2016年由Mirjalili等[23]提出的一种群体智能优化算法,源于对自然界中鲸鱼群体狩猎行为的模拟。整个算法过程包括包围猎物、泡泡网捕食、搜索猎物3个阶段。

(1) 包围猎物

假设在k维空间中,已有鲸鱼找到包围猎物的最佳位置,则其他鲸鱼会选择这个位置靠近,数学模型为:

(9)

(10)

C=2r1

(11)

A=a(2r2-1)

(12)

a=2(1-t/Tmax)

(13)

式中:r1和r2为区间[0,1]中的随机变量;a的值随着迭代次数t的增加,由2至0线性递减;Tmax为最大迭代次数。

(2) 泡泡网捕食

鲸鱼在驱赶包围猎物时有收缩包围圈和螺旋式向猎物游走2种方式。螺旋式向猎物游走是利用螺旋更新位置表示这种围捕行为,其数学模型为:

(14)

(15)

式中:Dk为鲸鱼到猎物的最优间距;b为对数螺旋形状常数;l为均匀分布在[-1,1]区间的随机数。

另一种围捕行为是利用收缩环绕机制,与包围猎物的数学模型公式基本一致,不同在于A的取值区间由[-a,a]调整为[-1,1]。

那么在鲸鱼捕食过程中以50%的概率为标准选用这2种方式的其中一种,即:

(16)

式中:p的取值区间为[0,1]。

(3) 搜索捕食

A值决定鲸鱼是向着最优个体游动还是向着随机个体游动,当|A|≤1时,鲸鱼选择向最优个体游动,如式(9),式(10);当|A|>1时,鲸鱼选择向随机个体游动,将会增强鲸鱼群体的全体搜索能力,数学模型为:

(17)

(18)

式中:Xrand是一个随机位置向量。

2.3 鲸鱼-决策树疲劳状态识别

鲸鱼-决策树疲劳状态识别算法(WOA-CART)流程见图4。

图4 鲸鱼-决策树识别算法流程

算法输入为构建的最优疲劳特征集D、基尼系数阈值和样本个数阈值;输出是CART分类树;根据参数集D,从根节点开始,递归地对每个节点计算节点内特征对数据集的基尼指数。

具体步骤为以下4步:

(1) 对每一个疲劳特征A,计算A中的每个取值a,根据疲劳样本点对A=a的测试为“是”或“否”,将D分割成D1和D2两个部分,并计算A=a时的基尼指数:

D1=(x,y)∈D|A(x)=a,D2=D-D1

(19)

对于参数集D,个数为|D|,在属性A的条件下,样本D的基尼系数定义为:

GiniIndexG(D|A=a)=

(20)

式中,基尼值公式为:

(21)

式中:p(xi)是分类xi出现的概率;n是分类的数目。

(2) 在所有可能的疲劳特征A以及它们所有可能的切分点a中,选择基尼指数最小的特征及其对应的切分点作为最优特征与最优切分点,从而生成两个子节点,并将最优疲劳特征参数集按特征分配到两个子节点中去。

(3) 对两个子节点递归地调用(1)、(2)直到满足停止条件;停止计算的条件是样本基本属于同一类。

(4) 在生成CART分类树的过程中,利用鲸鱼优化算法对树中的max_depth(树的最大深度)、min_samples_split(分裂一个内部节点需要的最少样本数)、min_samples_leaf(每个叶节点包含的最少样本数)、max_leaf_nodes(叶节点的最大数量)4个超参数进行优化,使决策树达到最好的分类效果。

3 试验与结果

3.1 试验数据

本文试验数据来源于VBOX平台,采样路径为北京至秦皇岛的一段全长约270 km的京哈高速公路。采集人数为5人,采集时长根据驾驶员在午后驾驶车辆约1～2 h就进入疲劳状态的实际经验,定为1～3 h,采集频率为100 Hz。根据同步脉冲信号可判定驾驶员面部视频和操作行为的一致性。以约1 min为标准对所采集的数据进行切分,随后依据驾驶员面部疲劳评分标准[22]给每一个所切分的数据段以0(清醒)、1(疲劳)和2(非常疲劳)打分。得到一个全新的疲劳驾驶样本数据集。将数据集中车速低于60 km/h的视为慢速路段,方向盘转角超过20°视为超车变道。剔除这些异常数据后的清醒样本有136个,疲劳样本71个,非常疲劳样本30个,共计237个样本,每个样本包含12维6 000行的操作行为数据。考虑到三级疲劳样本不均衡且样本过少,采用smote方法扩充清醒样本106个,疲劳样本171个,非常疲劳样本212个。

3.2 试验结果

在对所提取的统计指标进行正态性分析和方差齐性分析后,通过单因素方差分析,结合F值和P值,去除冗沉参数和相关性不大的特征参数后,最终选用了表1所示的5个指标作为最优疲劳特征集D。

表1 最优疲劳特征参数集

本文搭建的WOA-CRAT疲劳驾驶识别模型采用交叉验证方法,样本群数设置为10。对最优特征参数集D进行归一化处理后按照8∶2的比例划分为训练集和测试集。交叉验证结果见表2,其中清醒状态识别准确率为78.43%,疲劳状态的识别准确为90.48%,非常疲劳的识别准确率为84.91%,总体的识别准确率为84.25%。

表2 WOA-CART与CART算法识别准确率 %

3.3 方法评价

本文除了准确率(Accuracy),还引入了精确率(Precision)、召回率(Recall)、漏报率(Condition positive)和F1-得分(F1-Score)4个评价指标对疲劳驾驶检测模型进行了更全面的综合评估。WOA-CART算法模型检测结果见表3。

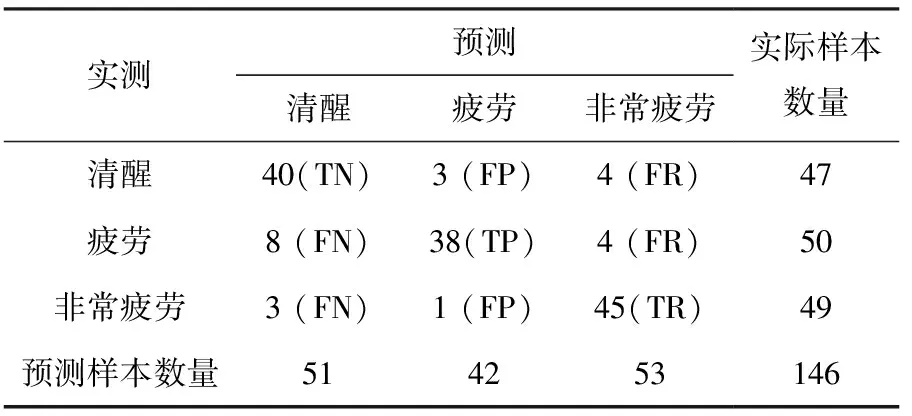
表3 WOA-CART算法模型检测结果

根据表3中的混淆矩阵:TN表示为正确预测为清醒的样本;TP表示为正确预测为疲劳的样本;TR表示正确预测为非常疲劳的样本;FN表示将清醒预测为疲劳和非常疲劳的样本;FP表示将疲劳预测为清醒和非常疲劳的样本;FR表示将非常疲劳预测为清醒和疲劳的样本。以清醒样本为例,各评价函数公式如下:

(1) 精确率:

P=TN/(TN+FN)

(22)

表示实际为正的样本在被预测为正的样本中的概率。

(2) 召回率:

R=TN/(TN+FP+FR)

(23)

表示被预测为正的样本在实际为正的样本中的概率。

(3) 漏报率:

CP=1-TN/(TN+FP+FR)

(24)

(4) F1-得分:

F1=2·R·P/(R+P)

(25)

根据以上定义,本文基于鲸鱼算法优化后的CART决策树疲劳驾驶检测模型评价结果如表4所示。模型精确率为84.60%、召回率为84.31%、漏报率为15.69%、F1-得分为84.16%。

表4 WOA-CART疲劳驾驶检测模型评价结果

4 结论

本文提出了一种基于鲸鱼优化的CART分类树方法对疲劳驾驶进行识别。首先对实车路况下的驾驶操作行为数据进行预处理,消除随机误差;然后利用单因素方差分析方法对提取的疲劳特征进行筛选,减少了模型选择疲劳特征的时间,响应速度加快;最后基于WOA-CART算法进行训练。经过鲸鱼算法优化后的WOA-CART疲劳驾驶识别模型总体识别准确率达到了84.25%,比未优化的CART模型提高了约9个百分点;相比于以单一方向盘转角为研究对象的疲劳驾驶检测[16],提高了约2%;漏报率为15.69%。本文提出的疲劳驾驶识别方法采用的实车驾驶操作行为数据,贴近实际工程应用,实用性得到提高。但本文所用试验数据样本偏少,未考虑到驾驶员个体差异性。因此在后续的研究中,需要扩充疲劳驾驶样本数据库,探究不同驾驶员之间的操作行为差异化,从而提高疲劳驾驶识别准确率和普及性。