基于出行者偏好特征的路径诱导方法研究

李文勇,黎顺虎,廉冠

(桂林电子科技大学 广西智慧交通重点实验室,广西 桂林541004)

智能交通系统是人、车、路所组成的复杂人机系统,如何对出行者进行更均衡的路径诱导是体现人机交互的热点问题,出行者偏好特征时刻影响着驾驶员的路径选择行为。目前的路径诱导方法考虑的因素过于单一,大多数都是在交通网络中利用路段行程时间作为路段阻抗,从而寻找最优诱导路径。但是由于出行者偏好特征的不同,其对各条路径做出的判断也会随之改变,往往让出行者很难做出合理的动态选择,并不能与出行者偏好更好地结合,无法满足多类型出行者的诱导出行要求。

Alder[1]基于虚拟路网分别通过路径诱导和交通实时发布信息对驾驶员路径选择进行影响行为分析。James等[2]利用路径选择模块和交通仿真模块共同搭建系统框架,进而研究驾驶员在信息系统中的运行效率,研究结果表明,盲目提高或降低交通信息服务占有率,会给出行者路径选择带来负面影响。高峰等[3]基于贝叶斯理论和多目标联合决策理论构建路径选择模型。Hussein[4]在不同的诱导信息条件选择倾向下,对出行者的路径选择进行研究,并构建了基于智能体方法的实时交通诱导信息影响下的出行者路径选择模型。Jou[5]深入研究了行程时间与出行距离等因素对出行者路径选择的影响,并由此构建了基于Probit模型的行程时间与出行距离联合的路径模型。Alexander[6]等为了让诱导结果接近系统最优解,进一步探讨了出行者的路径选择行为,重点分析总结了影响出行者路径选择行为的信息。张杨[7]以出行费用最小化为出发点,根据实时路网环境中出行者路径选择行为过程,构建了OD之间任意节点到终点的变分不等式模型,并给出了求解该目标模型的对角化嵌套算法。孙晓梅[8]主要研究多源交通信息下的出行者路径选择行为以及动态自适应路径诱导选择模型和算法。孙燕等[9]利用灰色系统理论建立寻路模型,且分析了出行者偏好对选择结果的影响。刘智萍等[10]基于免疫遗传优化提出了实时交通路径诱导方法,通过对路径评估、选择的反复择优,为出行者提供最优路径选择。

本文在以上研究方法的基础上,提出了一种基于出行者偏好特征的多属性决策路径诱导方法。出行者主观偏好能够更全面地在路径选择方法中体现出来,通过对出行特性偏好调查分析获取出行者偏好,用区间数的形式来表示目标路径客观属性值,且指标属性权重也在区间数的情况下,通过灰色关联分析法判断出行者主观偏好与路径客观信息之间的综合属性值。利用基于偏好的遗传算法进行求解,建立各个路径间的可能度矩阵及排序向量,可以很好地为智能交通诱导系统提供选择依据。

1 调查分析

综合考虑影响驾驶员出行的选择偏好,不同出行者对路径属性值有不同的心理侧重程度。本文通过出行特性调查分析选取路径选择偏好指标,能够充分反映驾驶员在日常出行中考虑的主要属性。

本次问卷调查的主题对象是桂林市的居民,调查问卷主要来自现场调查以及网上问卷,回收填写完整的问卷546份,得到有效问卷486份,问卷有效率为89%。

(1)出行者个人特征属性

本文出行者个人特征属性见表1。

表1 出行者个人特征属性

(2)出行者出行属性信息

居民出行目的分布见表2。从驾驶员出行目的的分析结果可知,上班/上学的驾驶员所占比例达到了36.31%,其次为回家/探亲(所占比例为29.75%),休闲/旅游、就医分别为25.34%、8.6%。

表2 出行目的分布

基于日常出行经历,所选出行路径属性中行驶距离、行驶时间、拥挤程度、出行费用、转弯次数、沿途景观、信号灯数量、出行经验、车辆组成成分、道路等级都影响出行者的决策,出行者选择路径方案主要偏好因素的重要度分析结果见图1。

图1 路径主要偏好因素的重要度分析

由图1可知,出行者选择替代路径主要因素重要度中,比较关心行驶时间、行驶距离、拥挤程度等属性,其得分均超过3.2分。通过SPSS软件对出行者路径选择行为与个人偏好之间进行相关度检验分析,得到偏好属性显著相异,后文建模将基于以上个人偏好因素进行。

本文首先对486条有效数据进行数据分析处理;其次对主要属性进行描述性分析;最后对各个解释变量(出行偏好因素)进行显著性分析,以期为后续的路径选择模型解释变量构建提供依据。

2 路径选择模型建立

考虑出行者偏好的路径选择问题目的是尽可能地减少路径客观属性和出行者主观偏好之间的偏差,本文的主要思路是把问题进一步转化为求解关联度问题,利用关联度的解决方式求解。

2.1 路径偏好目标描述

基于出行者对影响路径选择指标的行为偏好,本文以路径信息作为客观属性值,将出行者的偏好特征作为主观信息,进一步讨论路网寻优问题。由于交通网络存在很多不确定因素,出行者对各种主客观信息的判断不一,这就要求模型构建中要充分考虑出行者的主观视角。本文以综合建立考虑出行者偏好的路径选择模型,所建立的层次结构模型见图2。

图2 层次结构模型

2.2 灰色关联分析法

灰色关联分析法是灰色系统分析方法中的一种,能够准确地依据各因素之间的相近的发展趋势,权衡各因素之间的紧密程度。

(1)无量纲化处理

不同量纲造成各个指标的数据类型不同,为了消除不同变量不同量纲对决策的影响,对初始数据进行标准化处理。

(2)灰色关联系数计算

根据层次结构模型选出各指标层的最优指标值,组成参考数列。决策层各个可行路径的指标序列作为相对比较数列,由此计算各可行路径中的指标序列与相对应的指标参考序列的关联系数ξij。

(1)

2.3 有偏好的路径综合属性值计算模型

交通网络中,起点Sq到终点Sz有m条可选路径X1,X2,…,Xm(m≥2),出行者对任意一条路径的选择是由n个指标A1,A2,…,An决定的,每个指标An的属性值为区间数,则原始决策矩阵可表示为:

(2)

为了消除不同量纲对出行路径选择决策的影响,对初始决策矩阵进行标准化处理。

对于效益性属性:

(3)

对于成本性属性:

(4)

规范处理后的决策矩阵记为:

(5)

标准化处理后的决策矩阵表示出行者对可选路径的客观属性值。

出行者对可选路径的偏好特征向量可以表示为θ=(θ1,θ2,…,θm),0≤θi≤1,i=1,2,…,m,由此计算可选路径的客观属性值与出行者主观偏好值之间的欧式距离:

(6)

由于交通网络中多种条件的限制,为了满足出行者主观偏好路径选择特征,路径指标权重向量w=(w1,w2,…,wn)应使可选路径的客观属性值与出行者主观偏好值之间的关联度最大,为此建立如下指标权重最优模型:

(7)

由此关联度最优模型求得指标权重,进而对主观偏好值的综合属性值进行计算[11]。

各个路径方案的综合属性值为:

(8)

(9)

P=(Pij)n×n

(10)

其中:

(11)

对可能度矩阵P=(Pij)n×n采取排序向量求解:

(12)

由此得到排序向量v=(v1,v2,…,vn),按照vi的大小对可选路径进行排序,vi越大则代表其对应的路径更符合出行者的主观偏好特征。

3 路径选择模型求解算法

多目标优化问题[12]中的每一个子目标往往是彼此冲突的,一个子目标的优化改善可能会引起其他子目标性能的降低,因此通常不存在一个绝对最优解可以使得所有子目标同时达到最优,只能通过在各子目标之间进行区间控制协调,使得其目标函数都尽可能地达到最优。本文在多目标优化问题中引入Pareto最优解的概念,而进行多目标优化问题求解的核心就在于获得这些Pareto最优解所组成的集合。

本文将考虑出行者多个决策指标权重求解问题转化为多目标优化问题,将各个指标转化为目标子函数,问题描述为:

min{f1(X),f1(X),…,fn(X)}

s.t.i(X)≤0,i=1,2,…,m

(13)

式中:X表示决策指标;fi(X)表示目标关联度;gi(X)表示指标权重的约束条件。

定义2 支配关系

求解多目标优化问题时,假如可行解X(1),X(2)∈XCon满足以下关系:

(1)fi(X(1))≤fi(X(2)),即X(1)在所有目标函数上都不比X(2)差。

(2)X(1)至少有一个目标函数比X(2)的优,即在fi(X(1))≤fi(X(2))中至少有一个是严格不等式;则称可行解X(1)支配可行解X(2)。

定义3 拥挤距离

设{a,b,c,d}4个解的rank相同,下面将两个目标函数作为示例:

(2)对这4个解所得到的第一个子目标函数f1的值进行调整排序,由于f1的边界为a,d,由此使得a,d的距离为∞,则b,c的距离为:

(14)

(15)

(3)再根据第2个子目标函数f2的函数值对这4个解进行排序,因为这4个解处于同一个rank上,所以它们的排列顺序为{d,c,b,a},由此得出它们的拥挤距离分别为:

(16)

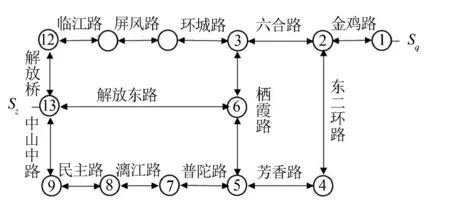
当个体的rank不同时,rank(i)

Step 1 参数初始化:定义初始种群中个体数量NIND、运算迭代次数MAX-gen、变量个数VNIND、外部种群集合中个体数目OutNIND;创建初始种群Chrom以及外部种群集合OutChrom,设置代数gen=0。

Step 2 计算种群Chrom中各子目标函数f1、f2、…、fn的具体值,根据f1、f2、…、fn的具体值以及支配关系定义计算初始种群中每一个个体的阶次值rank(i)以及拥挤距离。

Step 3 通过计算得到的阶次值和拥堵距离对Chrom进行轮盘赌选择,得到Chromparent,从而对Chromparent进行交叉变异操作,得到Offspring_Chrom。

Step 4 将Chrom和Offspring_Chrom进行合并得到下一代种群Chrom_1。

Step 5 判断Chrom_1中的所有个体是否处于偏好区域内,将处于偏好区域内的个体放到外部种群集合OutChrom中,得到新的OutChrom。

Step 6 对Chrom_1以及OutChrom中的个体进行非支配排序得到rank、计算其拥挤距离。

Step 7 通过rank和拥挤距离对Chrom_1和OutChrom进行选择,分别得到NIND个最优解的个体作为子代种群Chrom和OutNIND个数量的子代种群OutChrom。

Step8 gen=gen+1,若是gen≤maxgen,则跳转到步骤3,否则结束循环。

基于偏好的多目标遗传算法将进化过程中满足偏好的个体都转移到外部种群集合中,随之根据阶次值和拥挤距离对外部种群集合中的个体进行选择,并且这些个体随着遗传寻优过程同时进行进化。此算法不仅能够保证在整个目标空间内进行寻优,避免早熟现象,还能够在特定的偏好区内产生Pareto最优解。

4 实例分析

本文选取桂林市中心城区的交通网络作为实例分析对象,见图3。出行者从起点Sq到终点Sz,存在4条路径可以选择, 即路径A1: 1→2→3→6→13; 路径A2:1→2→3→10→11→12→13;路径A3:1→2→4→5→6→13;路径A4:1→2→4→5→7→8→9→13。将路网实例简化为交通网络,见图4。

图3 路网实例

图4 交通网络

考虑到出行者对可选路径指标层各个属性值的主观偏好不同。本文将每个指标都通过区间数来表示,采用0～9表示出行者的不同主观偏好值,例如行程时间为0表示时间成本最少,9表示时间成本最多。通过咨询有桂林市区域出行经验的专家,得到出行者给出的可选路径的指标区间数,经过数据分析处理得到各路径属性的原始区间数,见表3。

表3 路径各属性区间数

求出路径各属性的权重也为区间数:

测定出行者对可选路径各个因素的主观偏好值:[0.3,0.5],[0.5,0.7],[0.3,0.6],[0.4,0.7],[0.4,0.5],[0.3,0.6],[0.2,0.5],[0.4,0.7],[0.4,0.6],[0.3,0.4]。

在这个多属性路径决策中,属性类型分为成本型和效益型两类,其中拥挤程度、行程时间、行程距离、出行费用、转弯次数、信号灯数量、车辆组成成分为成本型属性,沿途景观、道路等级、出行经验为效益型属性。

规范化后的决策矩阵为:

(17)

则可选路径的客观属性值与出行者主观偏好值之间的欧式距离为:

(18)

计算各条路径客观属性值对于主观偏好值的灰色关联系数为:

(19)

则权重目标最优化模型为:

(20)

由路径求解算法解得路径各属性权重向量为:

由式(12)可得:

(21)

将Pij代入式(13)得:

v=(v1,v2,v3,v4)=

(0.216 7,0.225 8,0.280 9,0.276 6)

(22)

易见,v3≥v4≥v2≥v1。

可知v3对应的路径为最优路径,即路径A3是最符合第k个驾驶员出行偏好的路径。

由此可知,4条可选路径的指标层属性值均来自对桂林市中心城区路网比较熟悉的出行者,他们对桂林路网都具有丰富的出行经验。出行者给出的可选路径的指标属性值能够充分体现该区域路网的实际情况。利用本文提出的考虑出行者偏好的路径选择模型,对桂林市中心城区路网进行实例验证,4条路径的排序符合实际情况。

5 结论

基于路径诱导问题的多因素特点,进一步考虑出行者偏好和不确定性。本文提出了一种基于出行者偏好特征的多属性决策路径诱导方法,为出行者提供满意度最高的路径诱导建议。

(1)在出行者对影响路径选择有偏好的情况下,此方法能够充分利用标准化评价的先行信息,较好地反映出行者对路径各个因素的偏好侧重点,尽可能满足出行者的主观偏好。

(2)基于偏好的遗传算法,不仅能够保证在整个目标种群内进行寻优、避免早熟现象,还能够在特定的偏好区域产生最优解。

(3)智能交通系统是复杂的,出行者的偏好特征与交通网络的实时状态相互影响,如何将该方法动态的运用到智能交通诱导系统中,是下一步研究的重点内容。