平车转向架构架强度评估与优化

王剑,贺泰雄

(大连交通大学 机车车辆工程学院,辽宁 大连 116028)

随着我国铁路的快速发展,货车运输已成为我国铁路行业不可缺少的一部分,而转向架作为列车运行的关键承载部件,其平稳性、安全性以及寿命对货车的运营有着重要影响。构架作为转向架的主要承载部件,在服役过程中须具备足够强度以及使用寿命,确保货车运输的经济效益以及安全运营[1]。同时,随着对高性能转向架的深入研究,兼顾性能与质量的结构优化设计研究也日益成为研究热点。

目前针对车体以及转向架的优化主要集中在安全性、平稳性等动力学性能方面。邵晴等[2]对动车组转向架侧梁的焊接结构变形的影响因素进行了分析,并采用最优工艺参数的曲线T形接头使优化后的焊接变形降低了5.04%;黄志辉等[3]建立了一种适用于变轨距的体悬式电机变轨距转向架动车的动力学模型,并利用神经网络建立代理模型与多目标遗传算法进行优化,优化后满足相关标准,运行稳定性、平稳性等动力学性能有了显著提高;宫高霞等[4]对已有的动车组裙板结构进行结构优化,解决了头车裙板松动与裂纹的问题,并通过仿真分析验证了优化的合理性;邓斌等[5]针对转向架进行多目标优化,选择3个参数作为变量,采用响应面法拟合函数,并应用Matlab建立优化的数学模型,显著提高了优化的效率;刘文飞等[6]提出了一种用正交试验设计、BP神经网络、遗传算法相结合的优化方法对C80车体进行优化,从而提升车体结构的疲劳可靠性。

结构优化的方法主要分为拓扑优化、尺寸优化和形状优化。其中,拓扑优化是寻求结构最优的传力路径并在此基础上对结构进行改进,主要应用在产品的概念设计阶段。尺寸优化和形状优化是寻求在当前设计下的最优形状和尺寸,该方法主要应用在详细设计阶段。随着理论研究的深入与计算机技术的飞速发展,优化方法也日渐完善,例如针对拓扑优化的变密度法、水平集方法、渐进结构优化方法等[7],以及将智能算法如神经网络、遗传算法、模拟退火算法等运用到尺寸优化中,大幅度提高了优化求解的效率。在铁路机车领域,由于车体承载复杂,采用拓扑优化很容易影响到车体或转向架整体的刚度,因此在当前阶段,形状优化和尺寸优化是目前车体结构几何形状优化的主要设计方法。张明等[8]建立了B 型转向架构架模型,并利用APDL建立了参数化模型,采用遗传算法对构架进行优化,并根据优化结果进行试验分析,优化后结果满足强度要求与试验结果保持一致。邵微等[9]根据大变形碰撞理论,应用OptiStruct对车体的防撞装置进行优化,优化后质量减轻了33.6%,最大撞击力减小23%,提高了车辆的被动安全性。

本文采用一种基于有限元法的形状优化与几何重构的尺寸优化相结合的方法,来解决转向架构架应力集中以及轻量化的问题。以某平车转向架构架为例,应用HyperMesh建立构架的有限元模型,根据TB/T 3549.1—2019以及UIC 510—3进行加载与安全评估,并基于分析结果,对建立的有限元模型进行形状优化,改善构架横梁圆孔处的应力集中问题。在此基础上以质量最小为目标,强度要求为约束条件,构架中板肋的几何尺寸为设计变量,应用OptiStruct进行优化以达到轻量化的目标。

1 转向架构架的安全评估

1.1 构架有限元模型的建立

本文采用的平车转向架构架为H型,其结构主要由横梁以及两端侧梁组成(图1)。构架采用不同厚度的钢板焊接而成,所用材料为Q345E。

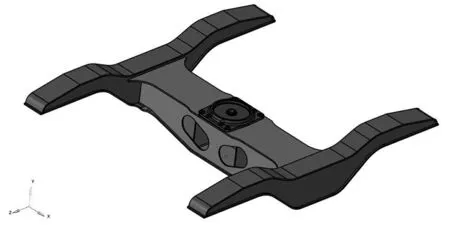
图1 转向架构架三维几何模型

有限元建模方式采用壳单元与实体单元混合建模[10],模型总计节点数为82 051,单元数为105 590。构架心盘采用四节点实体单元建模,横梁与两端侧梁采用壳单元,心盘与横梁用CP_STRUCTURE连接,在心盘与横梁螺栓孔处采用CE单元模拟螺栓连接、Beam188单元模拟螺栓。根据车轴、构架距轨面高度以及旁承位置,在构架四端用CE单元模拟车轴、旁承和转向架之间的连接,建立的构架有限元模型见图2。

图2 构架有限元模型

1.2 构架受力以及工况组合

转向架的质量为4 t,旁承间隙为1 956 mm,轴距为1 800 mm,两侧旁承间距为1 520 mm,车体自重为8.5 t,超常载重为30 t,运营载重为15 t,整备质量为16.5 t,最高运营速度为88 km/h。根据TB/T 3549.1—2019以及 UIC 510—3标准进行加载,分为超常工况和运营工况,由心盘和旁承共同承载。

1.2.1 超常工况

超常工况用于验证构架在极端载荷的作用下是否满足要求,主要考虑构架在垂向载荷、横向载荷、纵向载荷、菱形载荷以及扭转载荷的组合工况。

(1)垂向载荷

不考虑车体侧滚时,垂向载荷仅作用于心盘上,计算公式为:

(1)

式中:Fzp max为心盘垂向超常载荷;Fz max为转向架垂向超常总载荷;Mv为车辆整备状态质量;P1为车辆超常载重;nb为转向架个数,此处取2;m+为转向架质量。

考虑车体侧滚时,一部分载荷作用在一侧旁承上,另一部分载荷作用在心盘上:

Fzp max=1.5×Fz max(1-α)

Fz1 max=1.5×Fz maxα

(2)

(2)横向载荷

横向载荷作用于心盘上,计算公式为:

(3)

式中:ne为转向架上的轮对个数,此处取2;其余参数与式(1)相同。

(3)纵向载荷

纵向载荷等于转向架质量乘以运用中可能出现的最大加速度。纵向载荷作用于构架整体,平车时取值为5g。

(4)菱形载荷

菱形载荷施加在车轮位置,左右两侧方向相反,计算公式为:

(4)

(5)扭转载荷

超常载荷工况下,取10‰线路扭曲产生的载荷作为扭转载荷,运营工况下,取5‰。将各个载荷进行组合得到各个工况,工况与加载载荷见表1。

1.2.2 运营工况

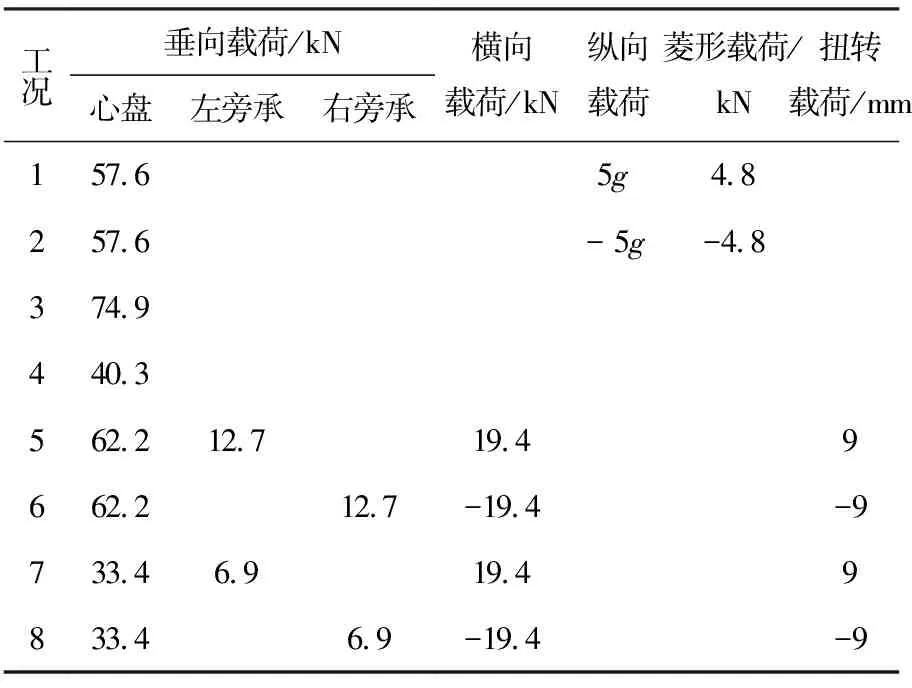
表2 运营载荷工况

1.3 强度分析结果

本文采用第四强度理论与基于无限寿命设计准则的Goodman-Smith疲劳极限法对转向架构架进行静强度评估与疲劳强度评估。

Goodman-Smith疲劳极限法利用有限元法计算运营载荷工况下构架结构的应力分布,得到构架结构每个节点的最大、最小主应力、应力幅和平均应力。以屈服极限为限界,以Goodman提出的线性经验公式为基础,用直线替代实际疲劳极限应力线后得到一种简化疲劳极限线图[11]。选取的评估点如果落在封闭折线之上或之外则表示经过107次循环之后会发生疲劳断裂,因此只有位于封闭折线内的点才是安全的。构架的材料为Q345E,选择抗拉强度Rm≥520 N/mm2的钢材疲劳极限图作为疲劳评估依据。

应用ANSYS对超常载荷工况和运营载荷工况进行求解得到有限元计算结果,构架在超常工况6下的应力云图见图3。选取运营工况中应力较大位置,提取相关应力数据,绘制疲劳极限图见图4。各个工况下的最大应力及其应力最大位置见表3。

表3 各个工况下的最大应力及位置

图3 构架整体Von Mises应力(超常工况6)

(a) 焊缝

在超常工况6下的最大应力为339.4 MPa,而安全系数取1.1时构架的许用应力为313 MPa,不符合构架的强度需求;选取的疲劳评估点均落在Goodman疲劳极限图中,构架符合疲劳需求。

2 构架结构优化设计

根据上述分析结果可知,构架在超常工况下部分位置的结构应力超过了材料的许用应力,不满足强度要求,故对其进行结构优化。本文对构架的结构优化采用形状优化与尺寸优化相结合的方法,首先对构架中不满足强度要求的位置进行形状优化,然后对其进行轻量化为目标的尺寸优化。

2.1 构架的形状优化

形状优化主要应用于产品的详细设计阶段,在产品受到无法改变的设计因素、工艺因素或成本制约时,通过改变产品局部的形状结构,达到降低应力集中、改善结构刚度的目的。在有限元模型中通过修改节点的位置即可达到修改结构形状的目的。转向架由于其复杂的受力以及其上安装有各种部件,采用形状优化可以很好地避免结构大幅度改变引起的一系列问题[12]。

构架在超常载荷工况6下,最大的受力位置在横梁腹板的孔处,对孔的形状进行优化以达到降低应力的目标。其数学模型为:

find:X(ni)

min:M=∑m(ni)

s.t.:σmax≤[σ]

(5)

式中:X为横梁孔的节点坐标;M为转向架的质量;[σ]取313 MPa。

应用OptiStruct对构架进行形状优化,优化前创建网格界限面限制,约束设计边界的总体变形。同时设置对称约束,避免优化后的结果不对称引起刚度的改变。优化前后横梁腹板有限元模型对比见图5。

图5 优化前后横梁腹板有限元模型

从图5中可以看出,优化前孔的形状为半圆和矩形组合的长圆孔,优化后长圆孔结构宽度方向收缩,整体为一不规则形状。分析优化结果,结构应力是由应变计算得到,应变来自结构变形,而结构变形受整体刚度控制[13]。在机械设计中,应采用逐渐变化的断面以防止刚度突变所导致的应力集中[14]。对于优化前由圆孔和矩形孔组合而成的孔,在其交界处由于曲率发生突变,导致了刚度不协调,由此导致应力集中,不满足强度要求。优化后孔周边主要受力部位的曲率变化较优化前明显降低,继而使得应力集中有所缓和。考虑在实际加工制造中,不规则的孔会导致加工变得复杂,成本难以控制,甚至难以实现,将优化后的孔圆整,近似为椭圆形状的孔(图6)。将其应用到有限元模型中重新计算,计算结果见图7。优化后构架在超常工况6下的最大等效应力为305.7 MPa,应力有下降。

图6 优化前与圆整后横梁模型

图7 形状优化后构架超常工况6的Von Mises应力

2.2 构架的尺寸优化

本文在上述形状优化的基础上,选取转向架构架各个板的厚度作为设计变量,取厚度的变化范围为初始值的50%。同时要求构架在超常工况下不超过安全系数1.1的许用应力,并以最小化构架质量为目标函数,构造的数学模型为[15]:

find:t=t(t1,t2,…,tn)

s.t.:σmax≤[σ]

tmin≤ti≤tmax,i=1,2,…,n

(6)

式中:t为厚度,t1,t2,…,tn为各个板的厚度;tmin和tmax为厚度的上下限;V为转向架构架的体积;[σ]为考虑安全系数1.1时材料的许用应力。

应用OptiStruct进行尺寸优化,根据尺寸优化结果取整,优化后各个板的厚度见表4。

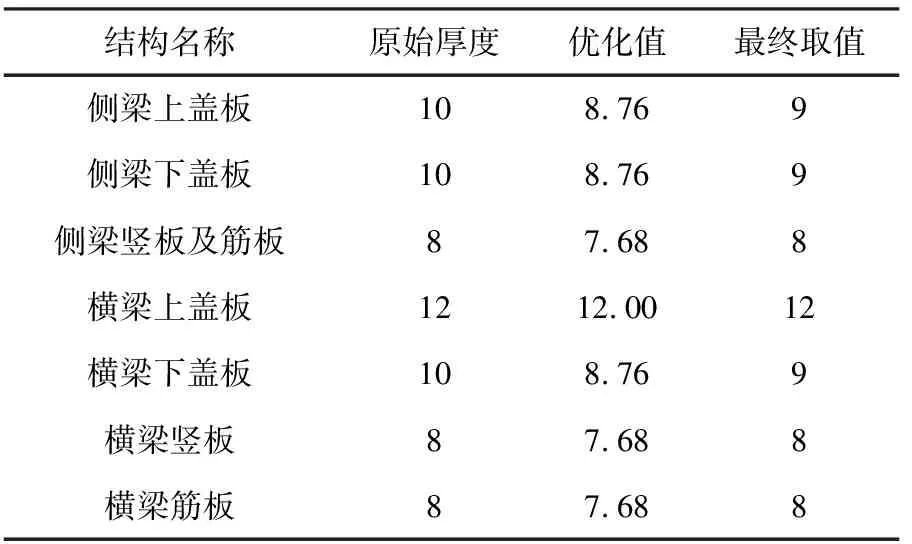
表4 尺寸优化前后构架的板厚 mm

优化后构架的整体质量降低了4.03%,将其重新进行强度分析与疲劳分析,结果见表5、图8和图9,可以看出优化后的静强度与疲劳强度满足要求。

表5 优化后强度超常工况分析结果

图8 尺寸优化后构架超常工况6的Von Mises应力

(a) 焊缝

3 结论

本文根据TB/T3549.1—2019标准对某平车转向架构架进行了强度与疲劳分析。在超常工况下,最大应力为345.4 MPa,原有结构不满足静强度需求,为设计人员指出了强度缺陷位置。

针对构架横梁应力较大的开孔处进行形状优化,使结构开孔曲率在原有应力集中位置的变化趋于平缓,改善了应力集中的问题。在形状优化的基础上进行减重为目标的尺寸优化,优化后构架整体质量降低了4.03%,最大应力下降了14.2%,满足静强度和疲劳寿命要求,实现了轻量化,构架受力也更加合理,计算结果可为转向架构架设计提供参考。