受电弓瞬态冲击强度及随机振动疲劳寿命仿真分析

胡超群,李永华,王悦东,田鸿博

(1.大连交通大学 机车车辆工程学院,辽宁 大连 116028;2.辽宁铁道职业技术学院 铁道机车学院,辽宁 锦州 121000)

受电弓作为列车顶部的受流装置,承担传输电能的重要作用,一旦发生事故,轻则造成受电弓损坏,列车无法前行,重则导致整条线路长时间停运。随着列车运行速度不断提高,受电弓弓网脱离接触,甚至结构上产生裂纹现象时有发生[1]。因此,为保证受电弓结构安全可靠,有必要对其进行瞬态冲击强度及随机振动疲劳寿命仿真分析。

目前对受电弓结构安全可靠性研究主要集中于可靠性分析[2-5],而受电弓结构安全方面的研究主要集中在弓网关系上。辜晨亮等[6]对新型高网受电弓焊缝处的疲劳强度进行了研究。吴文江等[7]利用有限元软件ANSYS Workbench对弓-网系统进行瞬态动力学分析,得出了造成吊弦鼓包与吊弦开股的主要原因与冲击振动相关的结论。贾荣等[8]对受电弓结构强度进行研究分析,计算得出受电弓结构的静强度和疲劳强度。李伟[9]根据线路试验历程载荷对受电弓弓头板簧进行寿命预计。除上述因素外,线路条件不平顺及弓网接触引起的瞬态冲击和随机振动都会导致结构损坏,也是影响受电弓结构安全可靠的原因之一。

综上所述,目前已有研究中对受电弓结构动力学特性缺少深入分析,而瞬态冲击和随机振动是结构动力学研究中的重要内容。因此,本文基于有限元法开展受电弓瞬态冲击强度和随机振动疲劳寿命仿真分析。首先建立受电弓有限元模型,施加IEC 61373:2010中冲击载荷计算受电弓的瞬态冲击强度,并改变结构阻尼比,计算其对冲击强度的影响。随后计算受电弓结构随机振动疲劳寿命,以IEC 61373:2010中ASD功率谱密度为激励,使用名义应力法和三区间法计算受电弓随机振动疲劳寿命,并对两种方法进行普适性分析。

1 理论概述

1.1 瞬态动力学理论

研究结构随时变激励作用下的系统动态响应特性常用瞬态动力学分析,多自由度系统在外力作用下的瞬态动力学方程为:

(1)

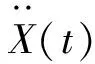
为避免结构发散,采用瑞丽阻尼模型反映真实结构阻尼,其定义式为:

C=αM+βK

(2)

式中:C为结构瑞丽阻尼矩阵;α为质量阻尼系数;M为结构质量矩阵;β为刚度阻尼系数;K为结构刚度矩阵[10]。

阻尼系数可以通过振型阻尼比ξi计算得出,ξi是某个振型i的实际阻尼和临界阻尼的比值。

根据瑞丽阻尼公式,阻尼系数α和β可以分别通过式(3)及式(4)计算[11]:

α=4πf1f2ξi/(f1+f2)

(3)

β=ξi/[π(f1+f2)]

(4)

式中:f1和f2为前两阶振型对应的自振频率。

本文使用ANSYS软件中的完全法计算瞬态冲击强度问题,完全法可使用精度高的Newmark逐步积分法求解[12]。

1.2 随机振动理论

区别于确定性振动,随机振动主要应用基于概率的功率谱密度分析载荷作用过程中的统计规律。工程中常用功率谱密度函数(Power Spectral Density,PSD)的谱参数表征外部激励。

PSD功率谱密度函数表达式为:

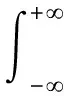
(5)

式中:Rxx(τ)为自相关函数。功率谱密度函数是自相关函数的傅里叶变换,通过逆变换可得:

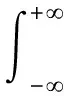
(6)

系统输出可表示为:

Sout(ω)=|H(ω)|2Sm(ω)

(7)

式中:ω为固有频率;Sm(ω)为PSD输入。

随机振动分析输入的内容包含了结构的固有频率、振型及功率谱密度函数,因此,在随机响应分析之前需要先完成结构的模态分析,求解出各阶固有频率。通过计算,能够输出各个方向功率谱密度函数。

对结构进行随机振动分析,目的是对在基于随机性的PSD作为激励载荷下的结构疲劳性能进行进一步分析。

1.3 基于三区间法的随机振动寿命计算

本文使用Steinberg提出的基于高斯分布和Miner线性累计损伤准则的三区间法进行分析[13]。该方法将应力分为±σ区间、±2σ区间、±3σ区间,应力幅值落在各区间的概率分别为0.683、0.271、0.043、应力幅值总概率为99.73%,而超出区间的部分只占0.27%,对结构损伤贡献较小。

根据以上理论,结构的累积疲劳损伤为:

D=n1σ/N1σ+n2σ/N2σ+n3σ/N3σ

(8)

式中:N1σ、N2σ、N3σ分别为3个应力区间对应的实际循环次数,D为结构累积损伤比。

则受电弓结构的疲劳寿命可表示为:

(9)

式中:V为所关心的频率;T为试验时间;L为受电弓疲劳寿命。

综上所述,本文技术路线见图1。

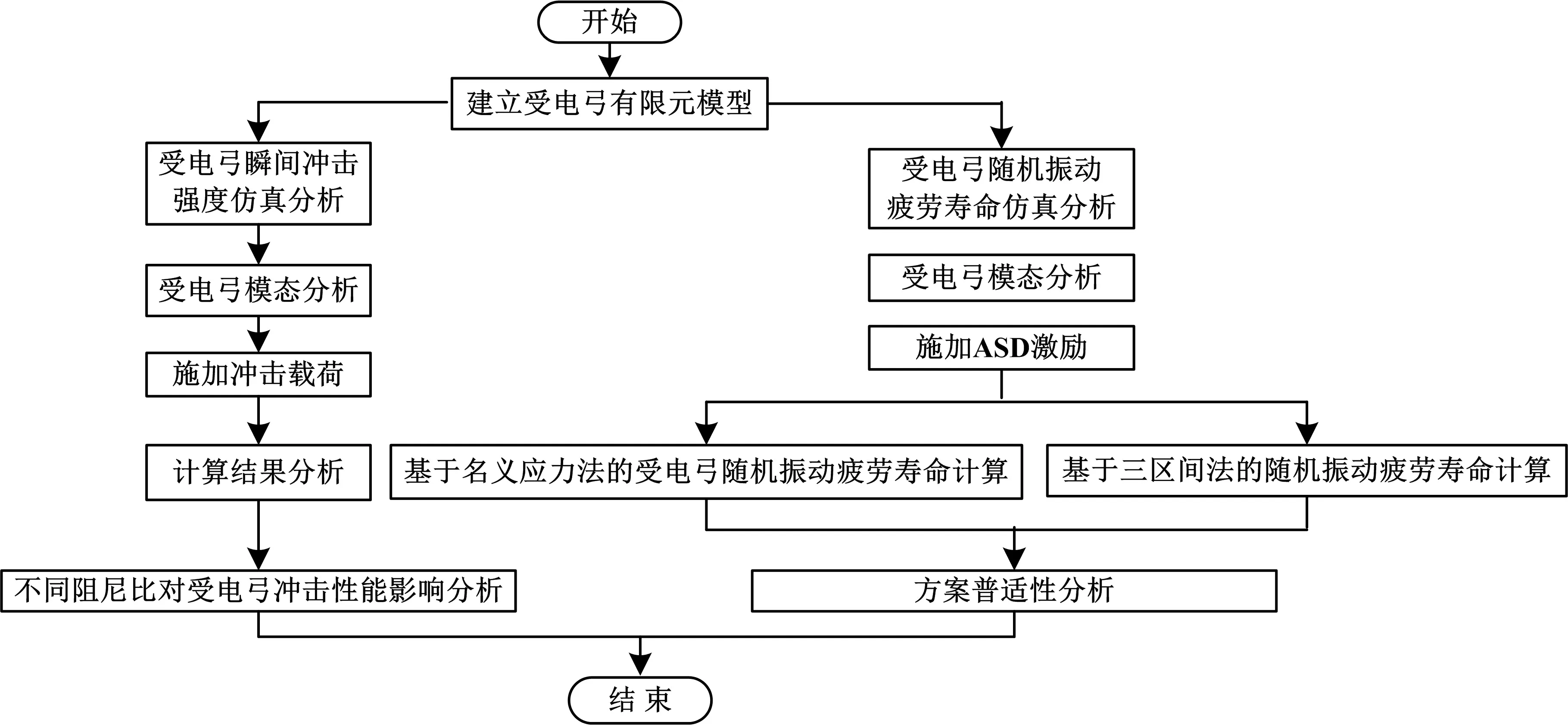
图1 技术路线图

2 受电弓有限元模型

材料以及材料屈服极限系数见表1。

表1 受电弓主要材料及力学性能

本文通过Hyper Mesh 17.0平台对受电弓的结构进行有限元建模,受电弓模型的单元总数为877 540,节点总数为545 295,整体质量约为85 kg,受电弓的有限元模型见图2。

图2 受电弓有限元模型

3 受电弓瞬态冲击强度仿真分析

本节基于ANSYS平台,施加冲击载荷计算受电弓结构的瞬态冲击强度。

3.1 受电弓约束模态分析

对受电弓整体结构进行约束模态分析,目的是求解受电弓结构的固有频率和固有振型,作为结构动力学计算所需要的参数。

主要污染物是指当AQI大于50时空气中最主要的一种污染物，其中二氧化硫（SO2）、氮氧化物（NO2）、可吸入颗粒物（PM10）、细颗粒物（PM2.5）和臭氧（O3）等已成为我国空气中主要的污染物[9]。西安主要污染物的月分布情况如图2所示，反映了近3年来采暖期主要污染物的变化规律。

在底架上的3个安装座部位施加约束,受电弓边界条件见图3。

图3 受电弓边界条件

受电弓结构一阶模态振型云图见图4,前20阶固有频率见表2。

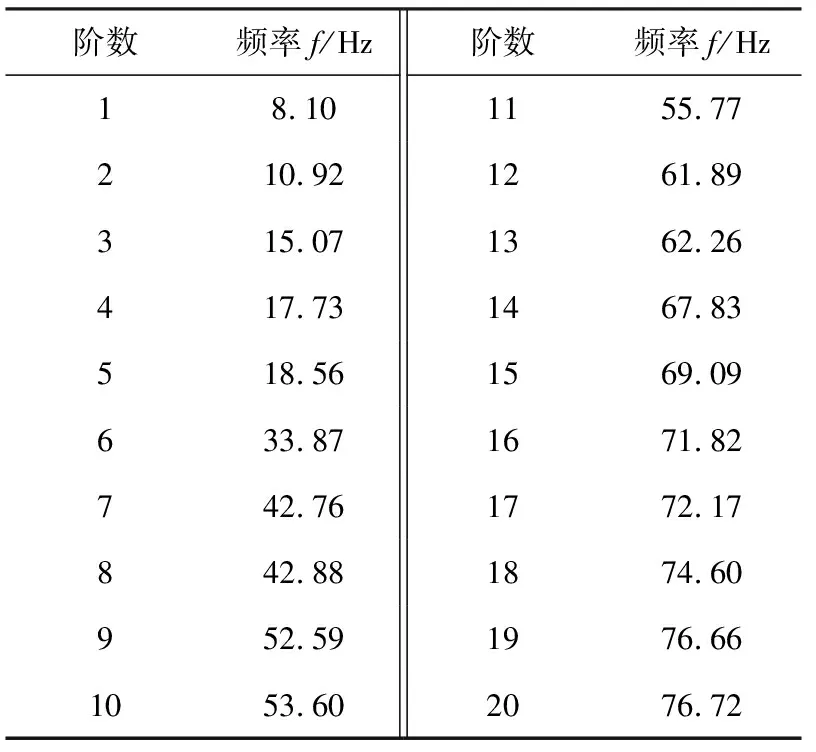
表2 受电弓前20阶固有频率

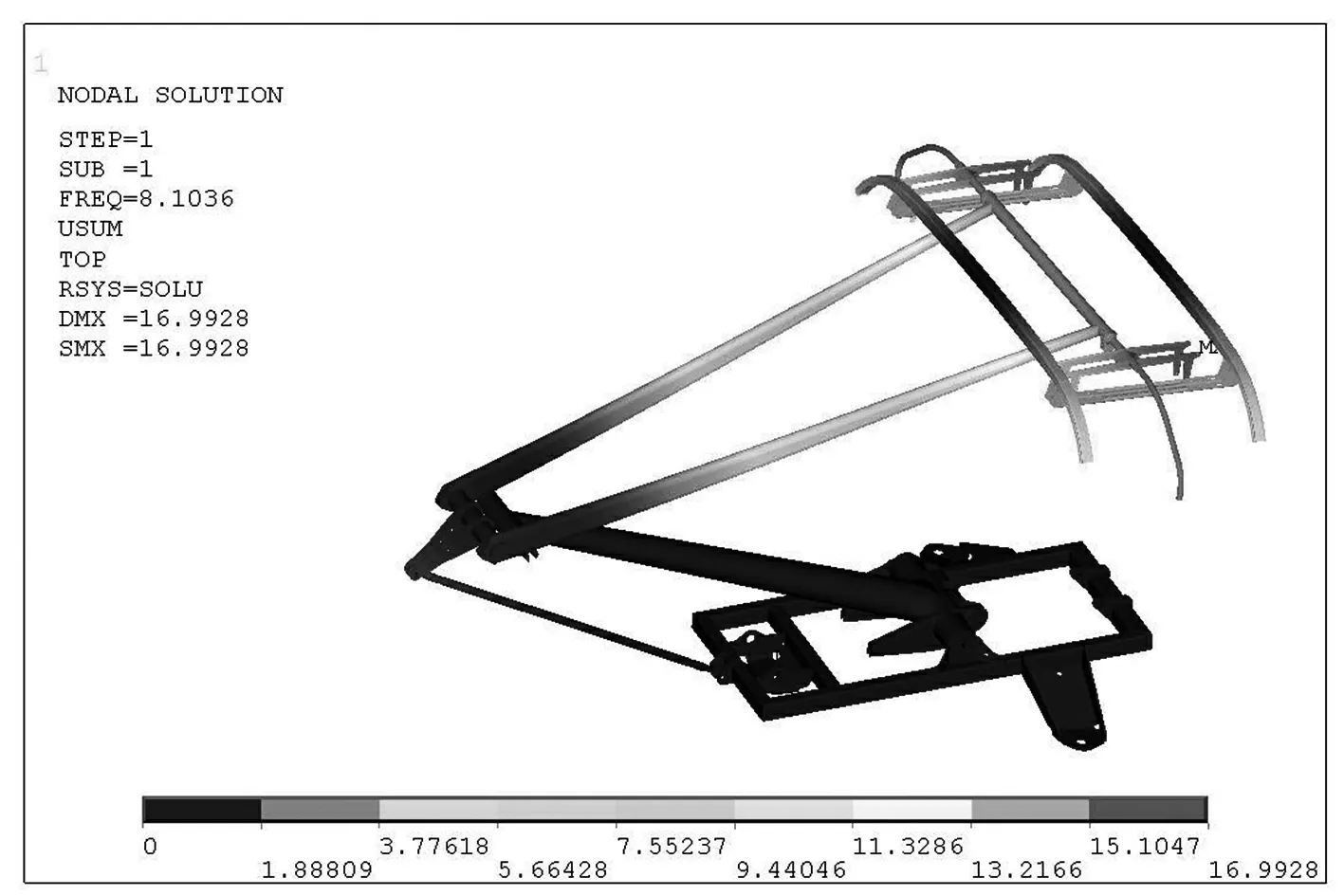
图4 受电弓一阶模态振型云图

3.2 冲击载荷施加

根据IEC 61373:2010规定,受电弓属于Ⅰ类A级车身装备,冲击响应分析的计算工况分为垂向、横向和纵向冲击工况。垂向、横向冲击加速度峰值均为30 m/s2, 纵向冲击加速度峰值为50 m/s2,3个工况脉冲宽度均为30 ms,冲击载荷从0 s开始施加,计算总时间设为0.10 s,设定为100步,计算时间间隔为0.001 s,设定的ξi为0.1,多自由度系统在外力下一般只能被激起较低的部分振型,大部分高阶振型一般可忽略不计。故根据模态的计算结果,选取前两阶模态频率作为计算最小及最大频率,可确定系统阻尼。

在受电弓底架与支持绝缘子3个连接部分约束除了冲击方向外的5个自由度,用刚性单元耦合3个约束位置,交点位置用一个大质量mass点作为施加冲击载荷的主节点。

纵向(X)载荷函数:

(10)

横向(Y)及垂向(Z)载荷函数:

(11)

3.3 冲击载荷计算结果

计算完成后,分别读取3个工况的Von.Mises应力值,结果见表3。

受电弓3个工况最大应力值点的应力见图5～图7。根据结果,最大应力处材料分别为不锈钢和铝合金,材料屈服极限为230 MPa和125 MPa,计算出的冲击强度应力均小于该部位材料的屈服应力,故均不会对结构产生永久破坏。

图5 受电弓纵向冲击计算结果(0.027 s)

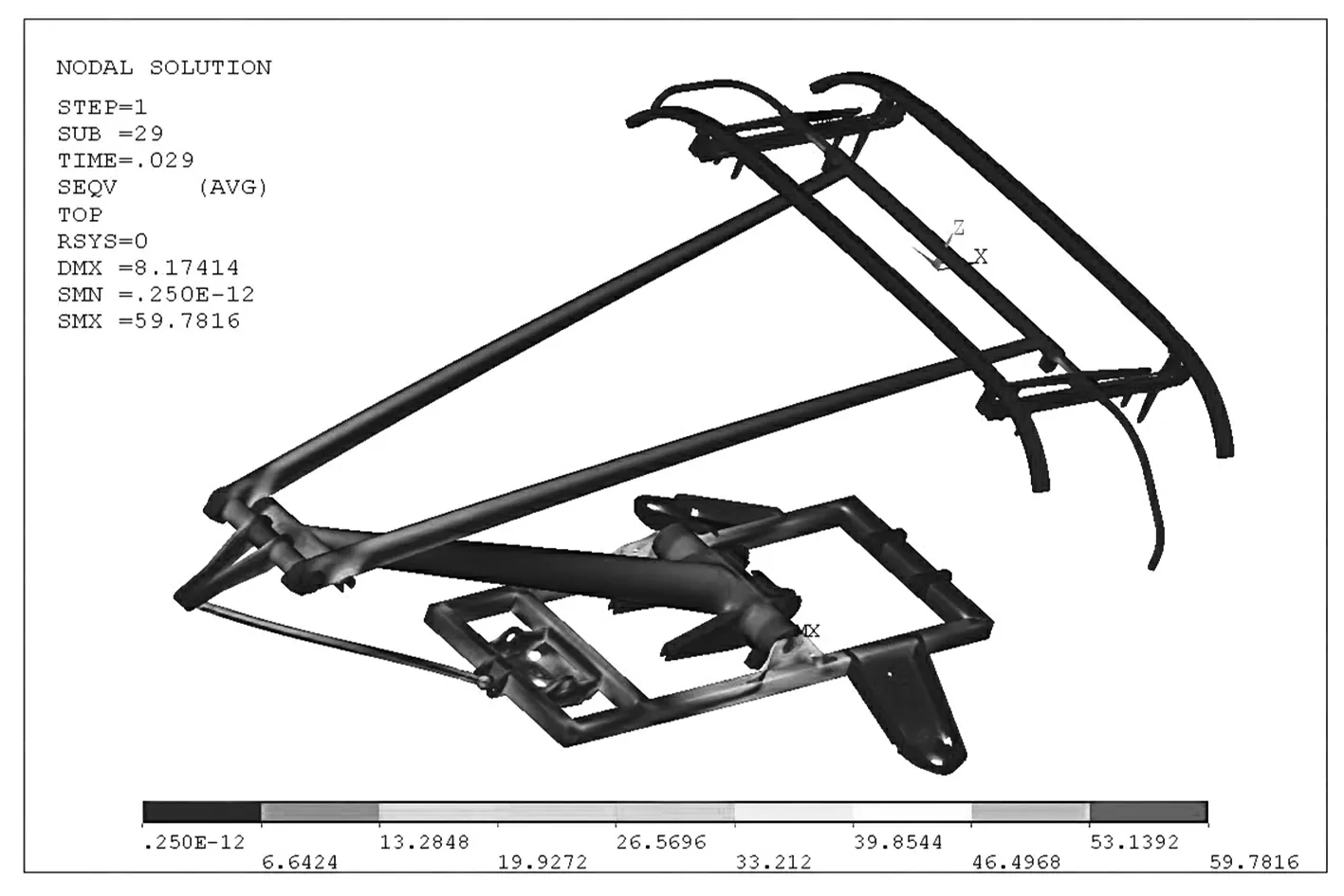
图7 受电弓垂向冲击计算结果(0.029 s)

3.4 不同阻尼比对受电弓冲击性能的影响

瞬态冲击分析中系统阻尼采用瑞丽阻尼,主要影响因素为质量阻尼系数α和刚度阻尼系数β,而α阻尼和β阻尼的主要影响参数为阻尼比ξi,故将阻尼比ξi作为变量,分析变量对受电弓结构冲击强度的影响。

以受电弓纵向工况为例,分别选取5%、10%、15%、20%共4个阻尼比计算阻尼系数α和β,输入值见表4。计算受电弓瞬态冲击强度,得到纵向工况不同阻尼比等效应力-时间曲线见图8。

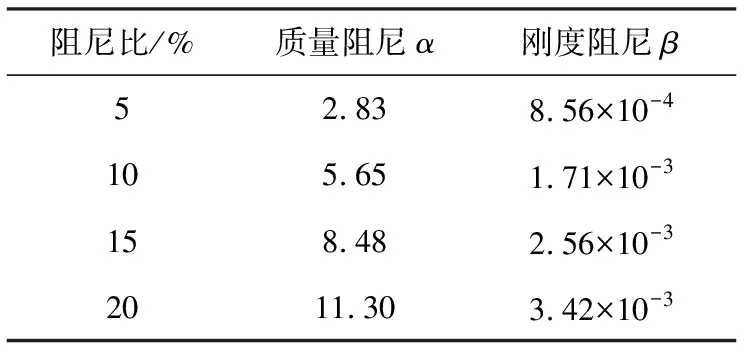
表4 不同阻尼比下的阻尼系数

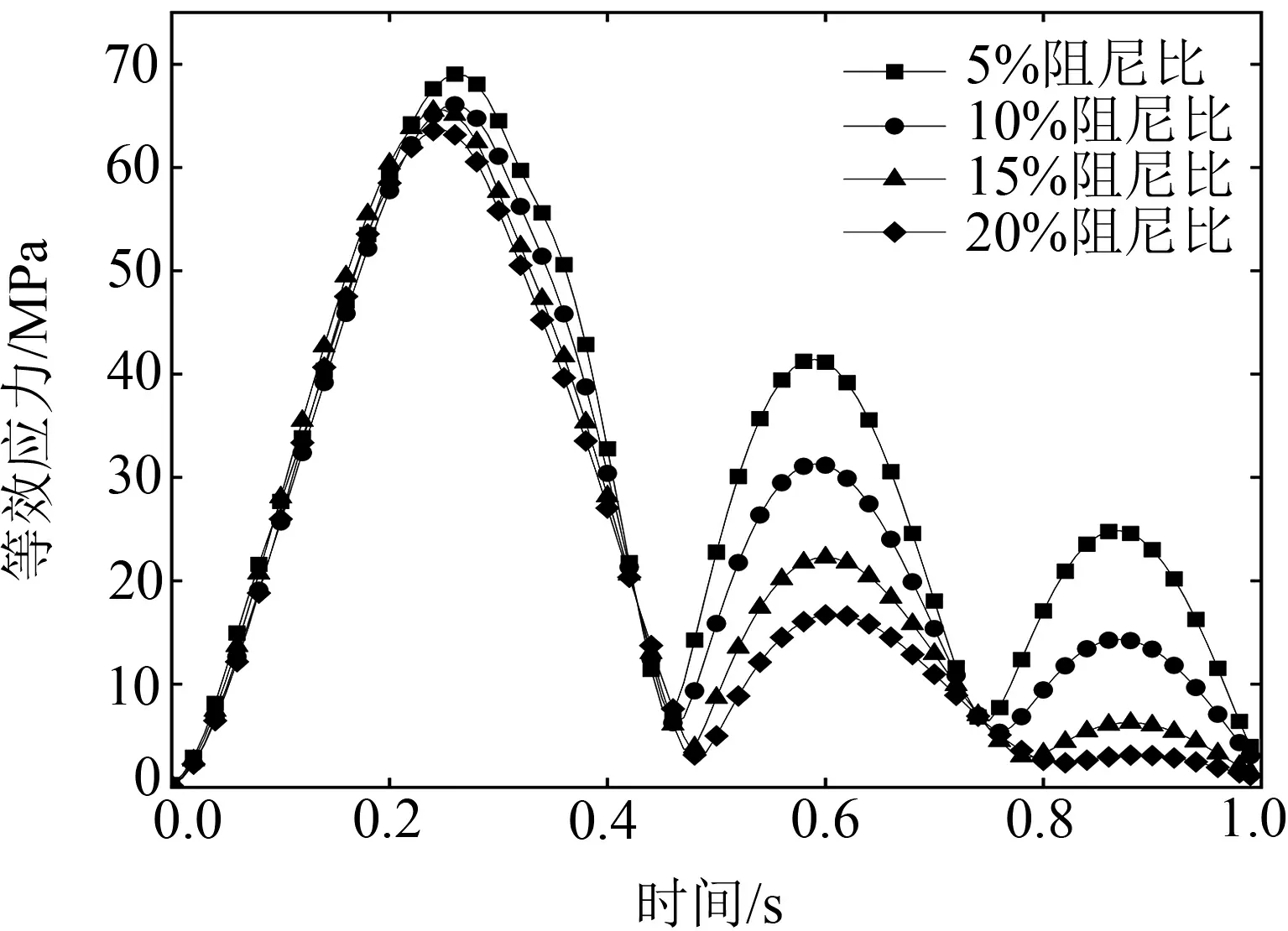
图8 纵向工况不同阻尼比应力最大位置应力-时间曲线

图8表明,不同阻尼比下,变量对第一个波峰值影响最小,随后依次增大。应力峰值出现在第一个波峰。随着阻尼比ξi的增大,应力值不断减小,故在实际工程应用中,可选用较低的阻尼比进行静强度设计,可满足工程实际需要。

施加冲击载荷的瞬态冲击强度分析没有考虑在基于随机性的PSD功率谱密度作为激励时的结构随机振动疲劳特性,下面对其进行计算分析。

4 受电弓随机振动疲劳寿命仿真分析

本文基于ANSYS平台,使用PSD功率谱密度作为激励,分析方法采用名义应力法和三区间法,计算受电弓结构随机振动疲劳寿命,并对方案进行普适性分析。

IEC 61373:2010中规定了安装在机车车辆上的设备进行随机振动疲劳试验的基本要求,目的是验证机车车辆在正常环境条件下承受振动的性能,标准中规定的试验方法为采用加速振动应力的方式来进行长寿命试验,通过对每个方向进行5 h的振动试验来等效使用25年机车车辆设备正常运行的振动疲劳损伤。

4.1 PSD谱施加

因PSD谱可为速度、加速度、位移等,故将IEC 61373:2010中规定的加速度谱密度谱(Acceleration Spectral Density,ASD)作为激励加载。

受电弓随机振动疲劳寿命计算分为纵向、横向、垂向3个方向的激励工况,根据图9计算出3个方向的ASD频谱密度。

图9 标准中A类车身安装设备ASD谱密度曲线

计算数据见表5。

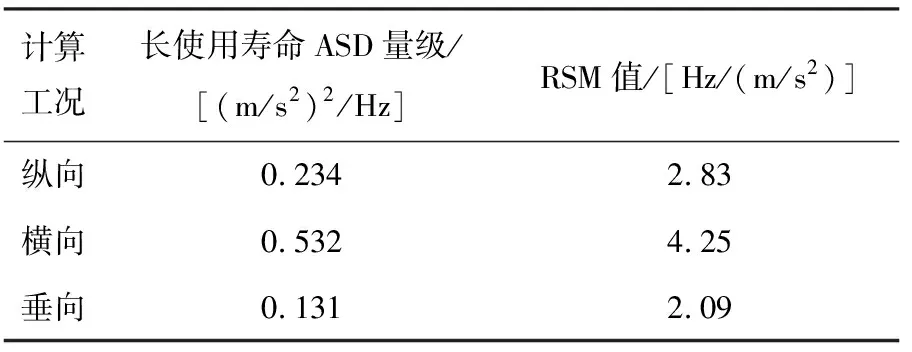
表5 A类车身安装随机振动试验参数

4.2 基于名义应力法的受电弓随机振动疲劳寿命计算

基于名义应力法[14],使用BS7608:2014[15]和IIW[16]中变幅疲劳破坏的评价标准,对受电弓的随机振动疲劳寿命进行计算,并对危险点进行评估。

施加激励后对3个工况分析计算,计算完成后分别提取3个工况应力值。

4.2.1 基于BS7608:2014的受电弓随机振动疲劳寿命计算

使用BS7608:2014中动应力引起的变幅疲劳部分,分析得出受电弓危险部位计算结果,见表6。累积损伤比最大处为F级焊缝,材料为不锈钢,应力值为10.3 MPa。

表6 各评估点评级及累积损伤比

4.2.2 基于IIW的受电弓随机振动疲劳寿命计算

基于IIW对受电弓中铝结构进行疲劳寿命计算,各个工况计算结果见表7。

表7 各评估点评级及累积损伤比

计算得出累积损伤比最大处为FAT等级36级焊缝,材料为5083铝合金,应力值5.15 MPa。

名义应力法计算得到受电弓重要部位评估点的累积损伤比最大值为0.84(小于1),受电弓结构满足疲劳设计要求。

根据式(12)可以计算在同等载荷线路谱可运行的总里程数:

K=KL/D

(12)

式中:KL表示受电弓在载荷谱下测试里程数。

选取焊缝处进行分析,根据修程规定,KL=200 万km,经过计算,K=238 万km,折合随机振动疲劳寿命为5.95 h,满足IEC 61373:2010中对长寿命振动试验5 h的要求。

4.3 基于三区间法的随机振动疲劳寿命计算

根据IEC 61373:2010,试验时间T取5 h。振动频率最大值为5 Hz,最大频率为150 Hz,取振动的最大频率V为150 Hz,根据式(9)可得:

(13)

通过在ANSYS的计算结果提取受电弓在3个工况上的Von.Mises应力数值,见表8。

表8 三个工况下的受电弓Von.Mises应力计算结果

3个工况下最大Von.Mises应力点即评估点1、2和3的部位分别属于下导管和底架,材料均为不锈钢,根据式(13)并结合文献中材料的S-N[17]曲线可计算出累计损伤比和寿命,具体结果见表9。

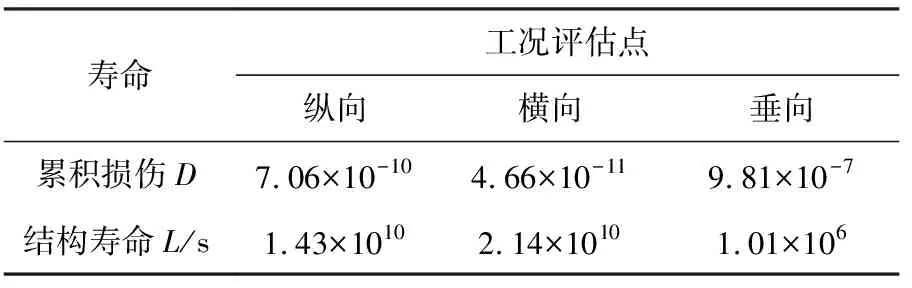
表9 各评估点的累积损伤比及寿命

由表9可知,累计损伤比最大值为9.81×10-7,3个评估点中振动疲劳寿命最小值为1.01×106s, 折合为277 h,表明当前结构满足耐久试验要求。

4.4 方法普适性分析

两种方法计算得出的结果表明累积损伤比均小于1。寿命值均满足IEC 61373:2010对长寿命振动试验5 h的要求。

对比两种分析方法:三区间法求解最大应力点所对应的循环次数,并将其进行叠加求解累积损伤比,计算出的结果接近于无限寿命,方法易求解,但计算结果和结构材料关系极大,没有考虑具体几何结构的影响。而名义应力法针对易损伤部位进行评估,比如焊缝处,螺栓孔等易发生疲劳断裂的位置,既考虑了材料,亦考虑了结构问题,名义应力法计算出的累积损伤较三区间法更高,主要是由于在BS7608:2014中针对动应力引起的变幅疲劳评价标准与恒幅疲劳中计算参数有很大的不同,相对来说更加严格。

因此,在工程实践中推荐使用整体-局部的流程计算随机振动疲劳寿命。先采用基于三区间法的疲劳寿命计算方法,对整体结构随机振动疲劳进行计算,然后基于名义应力法评估易发生疲劳损伤部位。这种评估流程可以使整体随机振动疲劳寿命计算结果更加可靠。

5 结论

本文基于有限元法,对受电弓的结构动力学特性结合IEC 61373:2010中的冲击振动载荷进行仿真分析,为受电弓瞬态冲击强度和随机振动疲劳寿命计算方法提供新的思路,具体结论如下:

(1) 受电弓在冲击载荷下纵向最大应力为72.87 MPa,位于底架支持绝缘子螺栓孔处;横向工况下最大应力为83.20 MPa,位于弓头支架处;垂向最大应力为59.87 MPa,位于下臂与底架轴承安装座连接处。材料为不锈钢及铝合金,小于该部分的材料屈服应力极限,受电弓结构强度满足设计要求,但在维修维护阶段应注意这3个位置,避免裂纹萌生及结构损坏。

(2) 改变阻尼比对冲击响应第一个波峰值应力影响最小,由于在较低阻尼下冲击载荷所对应的等效应力最大,若在较低阻尼工况下结果满足要求,就不必对其他阻尼进行进一步研究。

(3) 受电弓在ASD谱激励下,名义应力法计算出的累积损伤比最大值为0.84,位于底架焊缝处,三区间法计算出的累积损伤比最大值为9.81×10-7,计算出疲劳寿命累积损伤均小于1,满足疲劳设计要求。名义应力法及三区间法计算出随机振动疲劳寿命都满足IEC 61373:2010中振动耐久试验5 h要求,经普适性分析,结果表明先使用三区间法,再使用名义应力法的评估流程更适合计算结构随机振动疲劳寿命。