RC 梁构件基于能量的抗震设计方法研究
王玉奎,刘哲锋,张 丹,胡张齐
(1.湖南城市学院土木工程学院,湖南,益阳 413099;2.长沙理工大学土木工程学院,湖南,长沙 410004)
传统的抗震设计方法本质是基于峰值反应的抗震设计方法[1],该类设计方法反映了地震的幅值与频谱特性,但未能考虑地震持时对结构的影响[2-6],而基于能量的抗震设计方法中,包含了位移变形和承载力这两个重要的设计参数,同时考虑了地震持时引起的累积耗能损伤[7-8],进而能全面反映地震作用对结构的影响。同时,传统的抗震设计方法在避免结构倒塌和保障生命安全方面具有一定的可靠性[9-11],但未考虑到地震破坏造成的经济损失,基于能量的抗震设计理论通过结构重要性来决定其性能目标,并依次建立相应的抗震设防标准,在保证结构安全性能的同时,可以考虑“投资-效益”关系,进而满足经济需求。
1985 年AKIYAMA[12]通过对结构能量的研究,在理论层面提出了基于能量抗震设计的思路和方法,但该设计方法未能直接用于指导实际工程。同年PARK 和ANG 等[13-14]基于RC 梁(reinforce concrete beam,钢筋混凝土梁)、柱构件试验结果,建立了包含变形项和能量项的Park-Ang 损伤指数。在此之后,国内外学者开始以Park-Ang 指数为损伤评价标准来研究基于能量的抗震设计方法。FAJFAR[15]发现,为了保证Park-Ang 损伤指数小于1,结构在地震作用下的延性系数需小于单调荷载下的极限延性,因此提出通过限制结构在地震作用下的延性来补偿累积损伤带来的不利影响。 此后,CHAI 和FAJFAR 等[16]将这一构想进一步深入,通过将Park-Ang 损伤指数设定为1,提出了基于能量抗震设计的非线性设计谱。叶列平、缪志伟等[17-18]采用Park-Ang 指数进行梁、柱构件耗能损伤评价和能力设计,提出了基于能量抗震设计方法的实施框架和设计流程。YAGHMAEI-SABEGH 等[19]则针对Park-Ang指数的不同取值提出了基于延性约束的非线性设计谱。可见,各国学者都将能量指标成功地引入到结构设计流程中,对于基于能量的抗震设计向实用化发展具有重要意义,但由于Park-Ang 指数中变形项和能量项间的耦合作用尚未解析清楚[20],致使以Park-Ang 指数为损伤评价标准的设计方法其适用性还值得商榷。SHEN 等[21-22]和CHOU 等[23]则提出了钢框架结构基于能量的抗震设计流程,但进行构件性能验算时未能考虑变形指标,也未提出构件能力的设计方法。
前期课题组对RC 梁构件在变幅加载条件下的耗能能力衰变规律展开研究,建立了RC 梁构件耗能能力与位移幅值(变形项)、累积耗能(能量项)和结构设计参数的量值关系[24],并提出了RC 梁构件基于耗能能力的损伤指数和性能指标限值[25]。本文在既有研究基础上进一步提出RC 梁构件基于耗能能力损伤指数的抗震设计流程,并基于算例对该设计流程进行了介绍。
1 基于耗能能力的损伤指数
1.1 损伤指数Dk 的解析表达式
文献[25]中提出了RC 梁构件在变幅条件下的损伤指数Dk,其公式为:
式中:EH为前k个半滞回总累积耗能;My为构件截面屈服弯矩;θy为屈服位移角。
式中:μ¯为虚推平均名义半滞回位移,可由式(4)计算;ρsv为面积配箍率。
将式(2)~式(4)代入式(1),可得:
图1 是主要参数示意图。由式(5)可知,损伤指数Dk与结构设计参数(配箍率ρsv、截面屈服弯矩My和屈服位移角θy)和总累积耗能EH建立了量值联系。
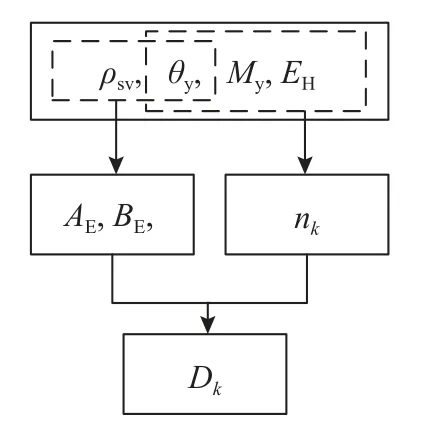
图1 主要参数示意图Fig.1 Schematic diagram of main parameters
在进行RC 梁构件设计时,梁端屈服位移角θy可由式(6)求得[26],梁端屈服弯矩My可由式(7)求得[27]。
式中: εy为纵向钢筋的屈服应变;l为梁的跨度;h为梁的截面高度。
式中:fy为纵向受拉钢筋的屈服强度;As为受拉钢筋的面积;h0为梁的截面有效高度;αs为纵向受拉钢筋的重心到梁底边的距离。
1.2 相关参数对损伤指数Dk 的影响规律分析
当RC 梁构件截面确定后,截面屈服弯矩My和屈服位移角θy仅与纵向配筋有关。因此,根据式(5),讨论配箍率ρsv、纵向配筋率ρs和总累积耗能EH对损伤指数Dk的影响规律。图2 是RC梁配筋参数和总累积耗能对损伤指数Dk的影响规律,其中,纵向大配筋率ρs,l时,Myθy取值为1200 kN·mm,纵向小配筋率ρs,s时,Myθy取值为600 kN·mm;图中,配箍率ρsv的取值区间为0.1%~2%;总累积耗能EH的取值区间为0 kN·mm~25 000 kN·mm,损伤指数Dk的取值区间为0 ~1。
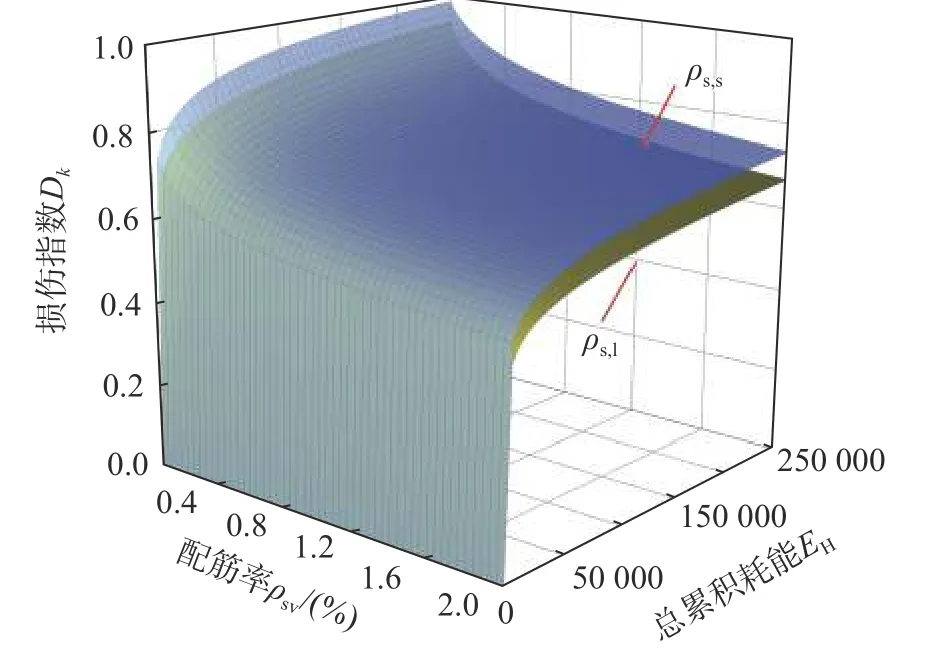
图2 RC 梁构件配筋参数和总累积耗能对损伤指数Dk 的影响规律Fig.2 The influence of reinforcement parameters of RC beam members and total cumulative energy dissipation capacity on damage index Dk
由图2 可知,随着总累积耗能EH的增加,损伤指数Dk由0~1 单调递增,即RC 梁构件的损伤程度从完好向破坏逐渐变化,且加载前期构件损伤发展较快;配箍率ρsv的增大可使构件损伤减小,但损伤减小效果先急后缓;对比ρs,l和ρs,s条件下的损伤指数Dk,可以发现纵向配筋率ρs的增加,可以整体上减小RC 梁构件的损伤。
1.3 损伤指数Dk 与地震参数的量值联系
为建立损伤指数Dk与地震参数之间的量值联系,式(5)中的总累积耗能EH采用KUNNATH等[28]提出的单自由度结构体系累积耗能的计算方法进行求解,单位质量总累积耗能EHµ的公式为:
式中:α 为比例参数,FAJAR 等[29]建立了比例参数α 的求解公式,见式(9);E1为单位质量的地震输入能量,可由式(10)计算。
式中,µ为结构的延性系数。
式中:PGV 为地面峰值速度;Ωv为地面峰值速度的放大系数,由式(11)计算。
式中:λ 与地面的场地类型有关,II 类场地时,λ 取值0.5;T为结构自振周期;Tg为特征周期,VIDIC等[30]提出了特征周期Tg的求解方法,见式(12);为输入能量谱峰值的放大系数,由式(13)计算。
式中:PGA 为地面峰值加速度;ca为弹性谱加速度与地面峰值加速度的比值,一般取2.4;cv为弹性谱速度与地面峰值速度的比值,一般取1.9。
式中,td为地震持时。
由式(8)~式(13)可得到单自由度结构体系单位质量的累积耗能EHµ,把单位质量的累积耗能EHµ与结构质量m相乘,即可获得单自由度结构体系的总累积耗能。把单自由度结构体系的总累积耗能,按照不同RC 梁、柱构件之间的耗能分配机制进行分配,即可获得相应RC 构件的总累积耗能EH为:
把式(14)代入式(5),得:
由式(15)可知,损伤指数Dk与结构设计参数(配箍率ρsv、截面屈服弯矩My、屈服位移角θy、延性系数µ、自振周期T及质量m)和地震参数(地面峰值加速度PGA、地面峰值速度PGV 和地震持时td)建立了量值联系。
1.4 损伤指数Dk 的性能指标限值
文献[25]中对9 个不同配筋条件的RC 梁构件实施低周往复加载试验。试验过程中,在试件的东南方向和西北方向的固定位置分别放置一台高清照相机,每个半滞回加载结束时拍摄一张照片,同时采用裂缝测宽仪对裂缝宽度进行测量,采用黑色油笔对裂缝走势进行描画,详细记录试件在每个半滞回的损伤发展情况,用以探讨损伤指数Dk的性能指标限值。图3 是某一个试件的损伤发展过程。

图3 试件的损伤发展过程Fig.3 The damage development process of specimen
研究发现[25],9 个RC 梁构件在试验过程中的表观损伤发展过程大致相同,都经历了混凝土开裂、裂缝贯通、单向斜裂缝出现、交叉型的双向斜裂缝形成和纵筋屈曲几个损伤过程,且相同的损伤阶段,性能指标限值区间大致相同。因此,可采用损伤指数Dk对RC 梁构件(不同配筋和不同加载路径)的损伤发展过程给出统一的性能划分准则。
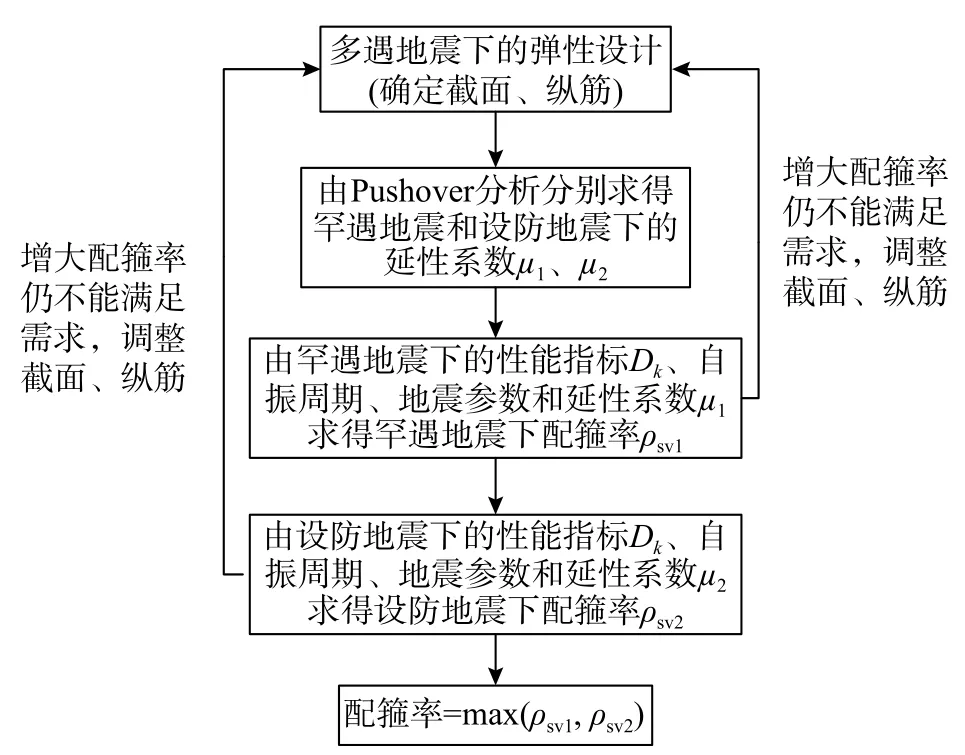
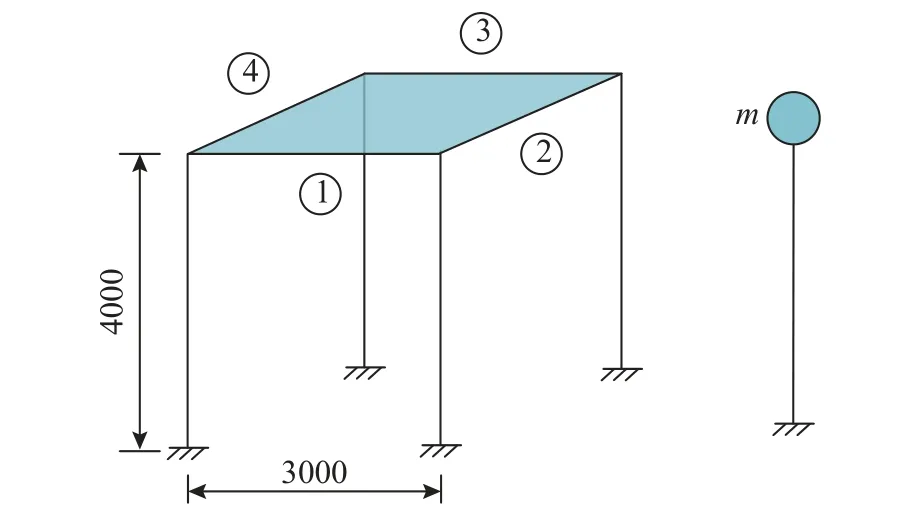
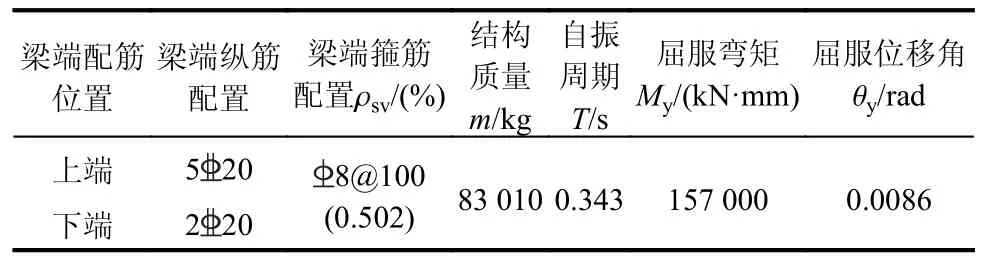
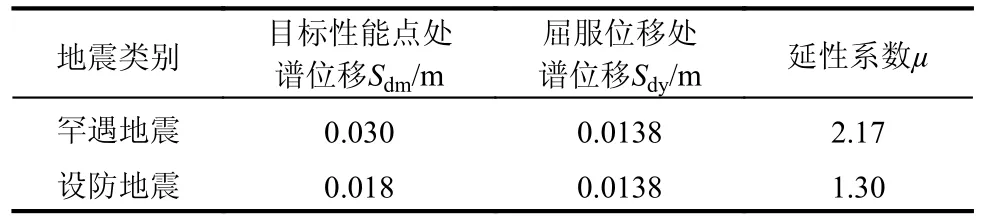
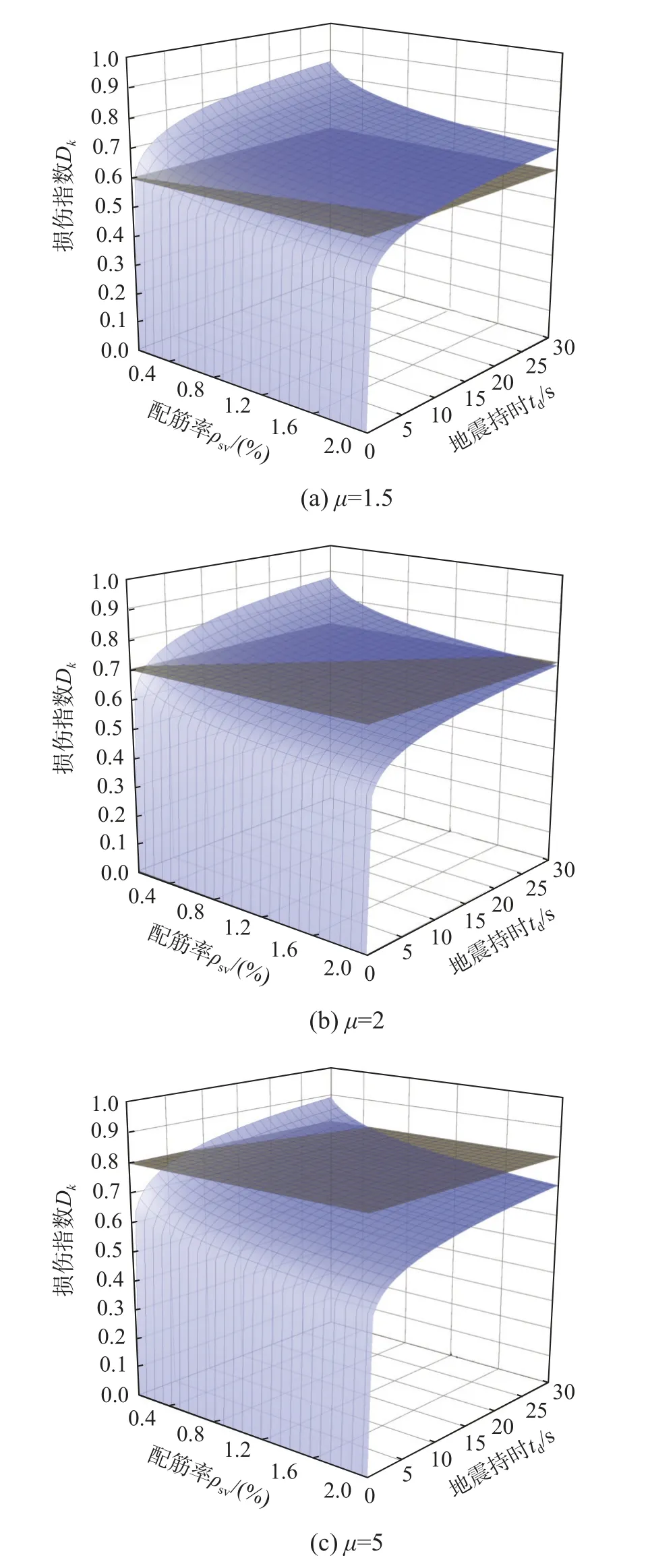
表1 给出了RC 构件基于损伤指数Dk的性能指标限值,其中,0 表1 RC 梁构件基于损伤指数Dk 的性能指标限值Table 1 The performance index limits of RC beam members based on the damage index Dk 在抗震设计时,截面屈服弯矩My、屈服位移角θy和延性系数µ与截面尺寸和纵向钢筋相关;自振周期T与质量m相关;地震参数由地面峰值加速度PGA、地面峰值速度PGV 和地震持时td确定。因此,根据式(15)可知,在性能设计时,当截面尺寸、纵向钢筋、自振周期和地震参数确定后,损伤指数Dk(性能设计目标)与配箍率ρsv建立了一一对应关系,即当业主根据需求提出性能目标后,设计者根据式(15)可以获得对应的配箍率ρsv。基于此,提出了RC 梁构件基于损伤指数Dk的抗震设计流程(图4 所示)。 图4 RC 梁构件基于损伤指数Dk 的抗震设计流程图Fig.4 The seismic design flow chart of RC beam members based on the damage index Dk 多遇地震下的弹性设计阶段与《建筑抗震设计规范》(GB 50011—2010)[27]一致,首先,初估目标构件的截面尺寸,由截面尺寸和混凝土材料获得侧移刚度。计算结构的重力荷载值,由弹性反应谱法确定目标构件的地震荷载效应,并验算目标构件在小震下的弹性变形,使其满足规范变形的要求。然后,依据地震荷载效应与其他荷载效应的最不利组合对目标构件进行配筋。根据截面尺寸和纵向配筋,可计算得到截面屈服弯矩My、屈服位移角θy,同时,根据结构的质量m和等效侧移刚度,可以获得结构的自振周期T。 采用有限元分析软件Midas Gen(2020 v2.1)对设计的单自由度结构进行非线性弹塑性Pushover分析,以获得结构的能力曲线,同时将规范中的加速度反应谱转化为需求谱曲线,将能力曲线与需求谱曲线进行比较,可以得到结构的目标性能点。分别采用罕遇地震下和设防地震下目标性能点处的谱位移值除以能力曲线上屈服位移处的谱位移值,即可对应获得到罕遇地震下和设防地震下的结构的延性系数µ1和µ2。 根据罕遇地震下的性能目标Dk值、截面尺寸和纵向配筋(屈服弯矩My、屈服位移角θy)、结构自振周期T、延性系数µ1值和地震参数(地面峰值加速度PGA、地面峰值速度PGV 和地震持时td),由式(15)计算获得罕遇地震下的配箍率ρsv1;同理,可获得设防地震下的配箍率ρsv2。 通过对比目标构件分别在罕遇地震下计算的配箍率ρsv1和设防地震下计算的配箍率ρsv2,选取二者较大值为目标配箍率ρsv。如果当配箍率的增加仍无法满足设计预期设定的性能目标时,则需要重新调整截面尺寸或增加纵向配筋,通过限制RC 梁构件的延性来达到设计预期设定的性能目标,然后根据提出的抗震设计流程重新匹配对应的配箍率。 本节以单自由度结构体系为算例(如图5 所示),介绍RC 梁构件基于耗能能力损伤指数抗震设计方法的具体应用。 图5 单自由度结构体系模型 /mmFig.5 Single degree of freedom structural system model 1) 设计参数 ① 地震参数:抗震设防烈度为8 度(0.2g),地震分组为第1 组,场地类别为Ⅱ类,建筑抗震类别为乙类。 ② 结构设计参数:混凝土强度等级为C35,保护层厚度取35 mm;纵向钢筋采用HRB400级,箍筋采用HRB335 级;柱子截面尺寸为400 mm×400 mm,梁截面尺寸为200 mm×350 mm;柱子高度为4000 mm,梁跨度为3000 mm;楼板厚度为100 mm,楼面荷载为80 kN/m2。 2) 多遇地震下弹性设计 多遇地震下的弹性设计阶段采用有限元分析软件Midas Gen 进行计算。由于4 根RC 梁构件的配筋相同,文中以①号梁为例进行介绍,RC 梁端的配筋及相关设计参数的计算结果见表2。 表2 RC 梁端的配筋及相关设计参数的计算结果Table 2 Calculation results of reinforcement of RC beam ends and related design parameters 3)µ值的计算 采用有限元分析软件Midas Gen 对设计的结构进行Pushover 分析,获得结构的目标性能点。图6 为结构的目标性能点。根据目标性能点处谱位移Sdm值和屈服位移处所对应的谱位移Sdy值,由式(16)可得到结构的延性系数,表3 为罕遇地震和设防地震下的延性系数。 表3 罕遇地震和设防地震下的延性系数Table 3 Ductility coefficient of RC members under rare earthquake and fortified earthquake 4) PGA 和PGV 的计算 在抗震设防烈度为8 度(0.2g)及建筑抗震类别为乙类的结构中,依据建筑抗震设计规范(GB 50011-2010)可知:罕遇地震下时程分析时所输入的地面峰值加速度PGA 为400 cm/s2;设防地震下时程分析时所输入的地面峰值加速度PGA 为196 cm/s2。场地类别为Ⅱ类及地震分组为第1 组时,地面地峰值速度与地面峰值加速度的比值取0.15 s[31]。因此,根据以上参数可以获得罕遇地震下的峰值速度为60 cm/s,设防地震下的峰值速度PGV 为29.4 cm/s。 5)td的选取 根据文献[31],地震持续时间td在0 s~10 s 区段时,RC 构件的损伤发展相对较快,地震持续时间在10 s~20 s 区段时,RC 构件的损伤发展速度降缓,地震持续时间在20 s~30 s 区段时,地震持续时间的增加对RC 构件的损伤发展的影响相对较小。因此,算例选取地震持时td分别是2.5 s、5 s、10 s、15 s、20 s 和30 s。 本算例中,由式(8)~式(13)可以获得单自由度结构体系的总累计耗能,在抗震设计时,为保证“强柱弱梁”及出于安全考虑,认为框架梁构件实现所有耗能[18],因此,采用总累计耗能除以RC 梁构件的塑性铰个数,即可获得目标RC 梁构件的总累计耗能EH。把目标RC 梁构件的总累计耗能EH和结构设计参数(屈服弯矩My、屈服位移角θy)代入式(5),即可计算获得不同性能水准下RC 梁构件的目标配箍率ρsv。 计算过程中不考虑梁箍筋的变化对结构非线性行为影响,图7 为RC 梁构件基于损伤指数抗震设计方法的配箍率计算结果。由图可见:① 当性能目标(损伤指数Dk)一致时,随着地震持时的增加,配箍率不断增加,可见持时的增加可加剧损伤的发展,性能目标越高(损伤指数越小)时,这种现象越明显;② 在相同地震持时条件下,配箍率的增加使损伤指数逐渐减小,可见增加配箍率可以有效减少RC 梁构件的损伤;该设计方法可弥补规范中未能考虑地震持时的不足。如,当业主选择损伤指数Dk=0.5 时,在地震持时(2.5 s~10 s)条件下,按照规范配置箍筋(规范配箍率为0.005 02)即可满足业主需求,但是当地震持时大于10 s 的情况下,按照规范配置箍筋不能满足业主预期的性能目标。 根据《建筑抗震设计规范》[27]中结构构件抗震性能办法可知,在罕遇地震下,第1 性能水准结构按线弹性设计,当控制延性系数µ<1,震后结构构件基本完好;第2 性能水准时,当控制延性系数µ<1.5,震后结构构件允许出现轻微破坏;第3 性能水准时,当控制延性系数µ≈2,震后结构构件允许出现中等破坏;第4 性能水准时,当控制延性系数µ≈5,震后结构构件接近严重破坏。表4是性能指标限值与规范中4 个性能水准的延性系数限值对应关系。 表4 性能指标限值与抗震规范中4 个性能水准的延性系数限值对应关系Table 4 Corresponding relationship between performance index limit and ductility coefficient limit of four performance levels in seismic code 为探讨本文提出的基于耗能能力损伤指数的抗震设计方法与规范中性能设计方法的区别,在上述算例基础上建立了不同延性系数的Dk-ρsv-td关系图(图8)。图中,配箍率ρsv的取值区间为0.1%~2%;地震持时td的取值区间为0 s~30 s;损伤指数Dk的取值区间为0~1。其中,当限制最大延性系数µ=1.5 时,表示根据规范中性能设计方法进行设计的结构构件,震后可保证轻度损伤;当限制最大延性系数µ=2 时,表示根据规范中性能设计方法进行设计的结构构件,震后可保证中度损伤;当限制最大延性系数µ=5 时,表示根据规范中性能设计方法进行设计的结构构件,震后结构构件呈现重度损伤。 图8 不同延性系数的Dk-ρsv-td 关系图Fig.8 Dk-ρsv-td relationship diagram under different ductility coefficients 由图8 可知:① 配箍率ρsv的增加,可以降低构件的损伤,但是损伤减小效果先急后缓;地震持时td的增加,加剧了构件损伤的发展,增加效果先快后慢;② 图8(a)中,随着地震持时td的增加,损伤指数Dk值超出了轻度损伤的性能指标限值(Dk=0.6)。同样,观察图8(b)和图8(c)可以分别发现,损伤指数超出了中度损伤的性能指标限值(Dk=0.7)和重度损伤的性能指标限值(Dk=0.8)。由此可见,随着地震持时td的增加,按照规范中控制延性系数的性能设计方法不能满足业主的预期损伤,而基于损伤指数的设计方法可以弥补规范中没考虑持时效应的不足。 本文以RC 梁构件为研究对象,通过建立耗能能力损伤指数与结构设计参数和地震参数的量值联系,初步阐明了单自由度体系下耗能发生在梁端的RC 梁构件基于能量的抗震设计方法,为将来“单”到“多”的抗震设计方法研究提供了一定参考。主要结论如下: (1) 提出了RC 梁构件基于耗能能力损伤指数的抗震设计流程,该方法与设计参数和地震参数建立了量值联系,便于指导设计。 (2) 配箍率的增加可以降低RC 梁构件的损伤,减损效果先急后缓;持时的增加可加剧RC 梁构件损伤的发展,增加效果先快后慢;配筋率的增加可以从整体上降低RC 梁构件的损伤。 (3) 基于耗能能力损伤指数的抗震设计方法,可以弥补规范中没有考虑持时效应的不足。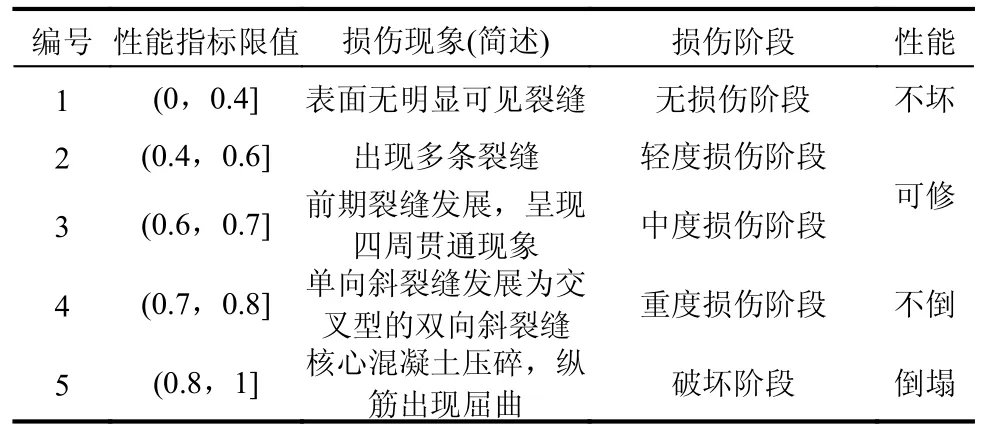
2 RC 梁构件基于耗能能力损伤指数的抗震设计流程
2.1 多遇地震下的弹性设计阶段
2.2 延性系数µ值的计算
2.3 配箍率ρsv 的计算
2.4 目标配箍率ρsv 的确定
3 算例
3.1 RC 梁构件基于耗能能力损伤指数的抗震设计
3.2 RC 梁构件基于耗能能力损伤指数的抗震设计结果
3.3 基于耗能能力损伤指数的抗震设计方法与规范中性能设计方法的对比

4 结论

