混凝土动态双轴压缩强度准则细观研究

李 健，金 浏，余文轩，杜修力

(北京工业大学城市减灾与防灾防护教育部重点实验室，北京 100124)

良好的抗压性能是混凝土的特点和优点之一。无论是在土木工程科学研究还是结构设计中，混凝土的单轴压缩强度普遍被用于理论计算与结构验算。《混凝土结构设计规范》(GB 50010-2010)[1](以下简称规范)对于混凝土结构承载能力极限状态计算和正常使用极限状态验算，大多将混凝土单轴轴心抗压强度标准值或设计值作为计算参数。实际上，混凝土结构在服役期内常处于多轴应力状态。对此，少数学者针对混凝土在多(双)轴荷载下的力学性能进行了试验研究[2-7]。研究结果表明：混凝土在多轴工况下的破坏模式、应力-应变曲线和强度等，均与单轴工况有明显区别。要了解混凝土的多轴力学行为，双轴工况是基础。综上所述，有必要对混凝土双轴力学性能，尤其是双轴抗压性能，进行深入研究。

正常使用的混凝土结构主要承受静荷载作用。但是，不可预知却具有强大破坏性的地震、冲击和爆炸等动态荷载时常会威胁建筑结构的安全[4]。混凝土是一种应变率敏感性材料，不同学者分别在动态单轴和双轴工况下对混凝土的力学行为进行了物理试验和数值研究[4-7]。研究结果表明，随应变率逐渐增大，混凝土试块的开裂裂缝逐渐增多，强度也逐渐增大。由于在动态荷载下开展物理试验，对试验设备和条件要求较高，并且数据收集较困难，目前对于混凝土材料动态力学性能的研究大多处于低应变率范围(10-5s-1≤ε˙≤10-2s-1)内。同样，混凝土双轴加载试验条件较单轴要求更高。总体而言，在有限的研究工作中，动态双轴试验相对较少，对于混凝土动态双轴力学性能的试验研究更不充分。

研究混凝土双轴强度准则，是研究其双轴力学性能的前提。目前，一些学者开展了相关试验来研究混凝土静动态双轴强度准则。表1 列出了包括规范在内的一些不同形式的强度准则。一方面，对于混凝土静态压-压强度准则，除规范建议的表达式外，由KUPFER 和GERSTLE 提出的“K-G”准则[8]也具有一定代表性。简化变形后的“K-G”准则可以直接反映混凝土压缩强度与侧应力比的关系，因此该准则得到了众多研究混凝土双轴强度准则学者的参考和验证[2-7,9]。另一方面，对于混凝土动态压-压强度准则，闫东明和林皋[9]考虑应变率和侧应力比对混凝土强度的影响，结合物理试验数据提出了适用于低应变率的动态双轴压-压强度准则。文献[4 - 7]分别对不同类别混凝土开展了动态双轴压缩试验，并对文献[9]提出的强度准则进行了不同角度的验证。此外，如表1 所示，程卓群等[10]在“K-G”准则基础上引入受应变率影响的动态强度，提出了“改进K-G 准则”。张玘璐等[11]仅将受应变率和侧应力比单独影响后的强度数值相乘，也得到了相应的强度准则。如上所述，目前混凝土静态双轴压-压强度准则已有较为完善的体系。由于动态试验数据少、离散性大，且不同学者选取的拟合方法多样，导致仅有的混凝土动态双轴压-压强度准则形式尚不统一，体系并不完善。另外，大多数物理试验仅能在低应变率范围内开展，导致据此提出的动态强度准则也仅适用于低应变率。那么，这些强度准则是否适用更高应变率范围还有待验证。近年来，低成本、高精度的细观数值模拟方法摆脱了传统物理试验条件的限制，为研究混凝土的损伤机理和力学性能提供了有效手段[12-19]。本研究应用细观数值模拟方法建立细观力学分析模型，在更高应变率范围内探究应变率和侧应力比对混凝土动态双轴压缩力学行为的影响，在对细观模型和模拟结果进行多角度验证后，建立静态、动态双轴压-压准则并进行初步验证。

表1 混凝土双轴强度准则研究现状Table 1 Research status of concrete biaxial strength criteria

1 细观数值模拟方法

1.1 细观模型

文献[14 - 19]考虑混凝土材料的非均质性，在细观层面将混凝土材料定义为由骨料颗粒、砂浆基质及两者之间的过渡区(interfacial transition zone，ITZ)等介质组成的多相复合材料。同文献[14 - 19]，本研究采用随机骨料模型来研究混凝土的力学行为。假定粗骨料为球形颗粒，粗骨料含量约为40%。采用二级配混凝土(含2 种骨料粒径颗粒：直径d为30 mm 的中石颗粒和d为12 mm的小石颗粒)。基于蒙特卡罗方法(Monte Carlo method)将骨料随机投放，生成混凝土立方体试件(如图1)。定义球形骨料与砂浆基体之间的等厚薄层为界面过渡区(ITZ)。需要说明：事实上混凝土内部ITZ 厚度约为20 µm～50 µm，但这为三维数值分析带来巨大计算量。KIM 和ABU AL-RUB[20]通过研究提出，ITZ 厚度对混凝土峰后的性能影响不大。SONG 和LU[21]进行了收敛性分析，发现ITZ厚度随名义网格尺寸在0.5 mm～2.0 mm 范围内变化，并且得出等效ITZ 厚度的相对变化只影响模拟结果曲线的下降段，而对应力增加阶段几乎没有影响的结论。因此，文献[14 - 19, 21 - 23]将界面过渡区厚度设置为0.5 mm～2.0 mm。为控制计算成本，本研究将ITZ 的厚度设置为1.0 mm，该设置方式已在文献[14, 17 - 19, 21, 24]中得到了验证。

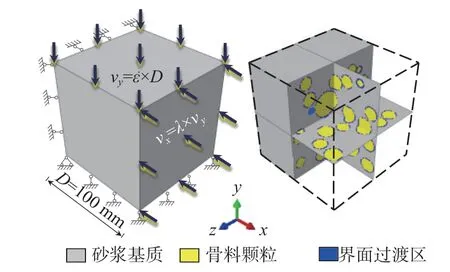
图1 3D 细观有限元模型Fig.1 3D Meso-Finite Element Model

另外，在本研究的动态荷载下，混凝土内部骨料颗粒会被贯穿而破坏。因此，为了建立与实际混凝土材料更加切合的数值模型，以得到更加准确的混凝土力学行为，参考文献[14 - 19]，对于描述混凝土内部组分的力学性能可采用如下处理方式：对于砂浆基质，其力学性能与混凝土类似；对于界面过渡区，可看作是孔隙率较高的砂浆，因此其力学性能可在砂浆基础上进行弱化。参考文献[14 - 19, 21]，ITZ 和砂浆基质的材料属性间可以用恒定比率表示。通过大量试验及试算确定，该恒定比率约为0.70～0.85。对于骨料颗粒，在动态荷载下，混凝土内部骨料并不都是弹性体，而是会在应变率作用下被拉断或劈裂，其力学性能可在砂浆基础上进行强化。在有限元分析中，本构模型可描述混凝土三相内部组分的力学行为。目前，塑性损伤模型[25-27]已广泛应用于混凝土类材料力学行为有限元分析[12,13,28-29]，下文将进行详细介绍。

本研究细观模型的边界条件设置如下：设置Y轴为主轴，X轴为侧轴，Z轴为自由轴。在试件顶部施加竖直向下的恒定速度vy= ε˙×D( ε˙为名义应变率)，在底部设置竖向固定约束；在试件一侧施加水平向速度vx=λ×vy(λ 为侧应力比)，在其对侧设置水平固定约束。

1.2 本构关系

目前，塑性损伤模型[13,25-27]已广泛应用于混凝土类材料力学行为有限元分析[12-19]。该模型假设材料破坏主要有压碎和拉裂两种模式，混凝土破坏面主要由等效塑形应变张量(拉应变和压应变)确定，混凝土材料刚度退化主要由两个独立的各向同性损伤变量(受拉损伤因子dt和受压损伤因子dc)表征，具体应力-应变关系可以表示为：

式中：σt为拉应力，σc为压应力；εt为拉应变，εc为压应变；为各向同性初始弹性模量。

多轴荷载作用下，等效塑性应变可用以下形式表示：

同时，经典Drucker-Prager 屈服面函数F可由以下形式表示：

式中，各参数可表示为：

基于以上塑性损伤模型，文献[12, 13, 28 - 29]通过细观有限元分析方法研究了双轴荷载下混凝土材料的损伤机理和力学性能。其中，ZHANG 等[12]应用塑性损伤模型分别在不同双轴工况下(压-压、拉-压、拉-拉)将模拟结果与物理试验结果进行了对比。结果表明，塑性损伤模型可以较好地模拟混凝土类材料在复杂荷载下的力学行为。

另外，考虑应变率效应，本研究采用强度放大因子(Dynamic Increase Factor，DIF)来表示混凝土内部组分的强度放大效应[4-6,9]。在动态双轴荷载下，混凝土强度DIF 可表示为：

式中：k为材料参数，反映混凝土材料受压时的率效应； ε˙ 为 动态应变率； ε˙s为静态应变率( ε˙s=10-5s-1)。

参考文献[7, 14, 18, 30]，本研究亦采用考虑应变率效应的塑性损伤模型对混凝土三相组分进行设置。此模拟方法已得到了申佳玉[7]和商怀帅[30]的物理验证。另外，参考文献[14 - 19]，为降低不可避免的网格敏感性问题，本研究将混凝土各组分达到抗拉强度后的应力-应变曲线替换为由HORDIJK[31]提出的“拉应力-裂缝宽度”曲线，该曲线具体表示为：

式中：ft为单轴拉伸强度；w0为拉应力下降为0 时的开裂宽度(w0=5.4Gf/ft，Gf为断裂能)。

1.3 模型验证

在本节中，为了验证上述细观数值模型和分析方法的合理性，对尚世明[4]开展的动态双轴压缩试验进行了等效细观数值模拟。表2 列出了混凝土材料各组分细观力学参数。其中，混凝土的单双轴压缩强度，密度和弹性模量E的取值参考文献[4]，其他物理参数如泊松比ν，由于物理试验尚未给出，本研究参考文献[14 - 19]来确定。图2 展示了在静态和动态单双轴工况下数值模拟结果与试验结果的对比。可以看出，无论是破坏模式还是应力-应变曲线，采用上述数值模型和分析方法得到的结果与尚世明[4]的试验结果吻合较好。同时，本研究数值模拟方法在任意组合工况下的可行性和准确性也得到了验证。

图2 模拟结果与试验[4]的对比Fig.2 Comparison between simulation and test results[4]

表2 细观组分参数Table 2 Meso-component parameters

2 模拟结果与分析

为研究应变率和侧应力比对混凝土动态双轴压缩强度的影响，进而讨论和建立混凝土双轴压-压强度准则，本研究设置不同应变率(低应变率：ε˙=10-5s-1(准静态)、10-3s-1、10-2s-1；中应变率：10-1s-1、1 s-1)和不同侧应力比(λ = 0 (单轴压缩)、0.25、0.50、0.75、1.00)的组合工况，对试件边长为100 mm 的立方体试件进行了动态双轴压缩工况下的数值模拟研究。

2.1 破坏模式

图3 展示了不同工况下的混凝土破坏模式。为了更清晰地比较不同工况下的混凝土试件在同一破坏阶段的破坏模式，本研究参考规范[1]，当混凝土主轴正截面极限压应变达到0.0033 时，将各个混凝土试件的破坏模式进行对比，以此来说明在同一破坏阶段下应变率和侧应力比对混凝土破坏模式的影响。一方面，相同应变率下，当侧应力比较小(0≤ λ ≤0.5)时，试件内部较为薄弱的区域(ITZ)首先出现损伤然后扩展到砂浆基质，损伤区域不断扩展和演化，最终形成斜向连贯的“柱状”裂缝。随着侧应力比增大(0.5≤ λ ≤1.0)，由于侧应力的“约束”作用逐渐增强，试件内部粗骨料被劈裂破坏，试件最终形成“片状”裂缝。另一方面，相同侧应力比下，随应变率增大，混凝土内部骨料破坏数量增多，裂纹数量增加，损伤区域增大。此时，侧应力比对混凝土破坏模式的影响随应变率增大而逐渐被削弱。

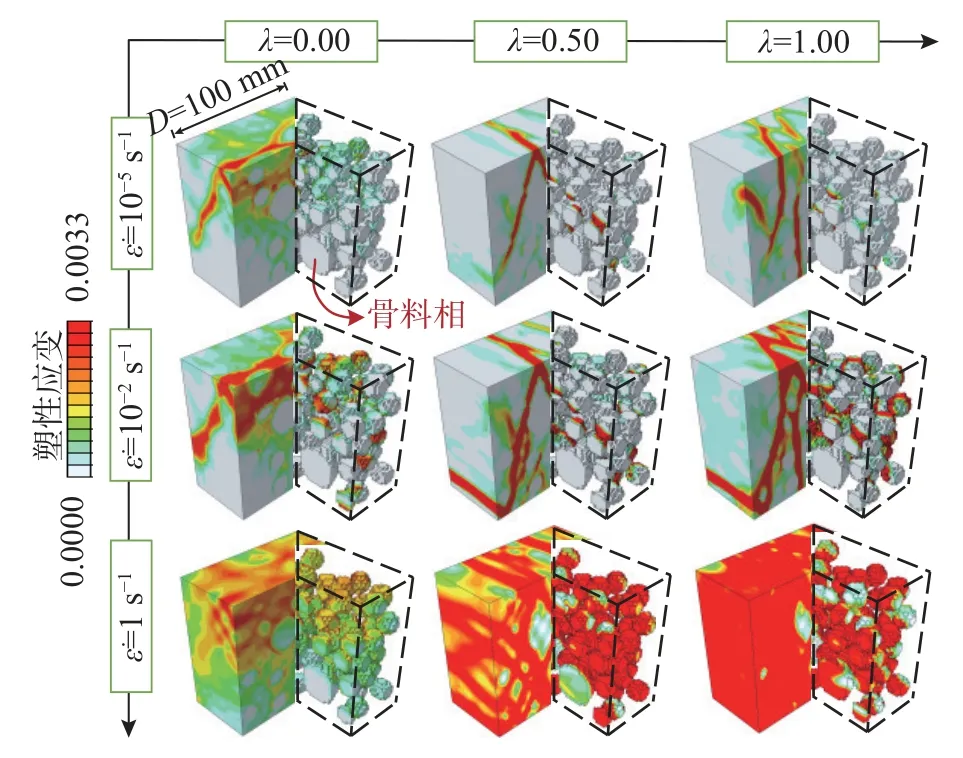
图3 不同工况下同一破坏阶段的混凝土破坏模式Fig.3 Failure modes of concrete in the same failure stage under different loading conditions

2.2 动态强度

参考文献[4 - 7]，双轴压缩工况下的混凝土强度为试件破坏时双向峰值应力的最大值。因此，本研究主要讨论混凝土主轴压缩强度，如图4所示。随着应变率增大，不同工况下的混凝土动态主轴压缩强度均增大。随着侧应力比增大，混凝土动态主轴压缩强度先增大后减小，在侧应力比为0.5 左右时达到峰值。不同侧应力比下混凝土的主轴压缩强度均大于其同工况下的单轴压缩强度。这是因为当侧应力比较小时(0≤ λ ≤0.5)，较小的侧应力限制了混凝土内部微裂缝的扩展和侧向变形的产生，降低了主轴方向劈裂失稳破坏的可能性。由于泊松效应，侧向约束作用随侧应力比增大而逐渐增强，制约横向变形的水平惯性抗力抑制或延迟了试件宏观裂缝的产生，使得材料破坏需要消耗更多的能量，因此双轴压缩强度不断提高。但是，当侧应力继续变大时(0.5≤ λ ≤1.0)，其产生的约束作用持续变强，这加速了混凝土内部微裂缝在自由面方向的产生和扩展，导致裂缝数量逐渐变多。同时试件由柱状失稳破坏变为片状劈裂破坏，耗能能力减弱。因此，双轴压缩强度逐渐降低。此时，由于侧应力并未消失，混凝土的双轴压缩强度依然高于其单轴强度。

图4 不同工况下混凝土双轴压缩强度Fig.4 Concrete biaxial compressive strength under different loading conditions

2.3 与试验结果对比

本节将对比数值模拟点与文献[5, 6, 11, 32]的试验点，来验证由上述细观数值模型和分析方法得到的试验结果的合理性和准确性。由于各物理试验条件尚不统一，这里首先对试验数据进行“归一化处理”(即动态主轴压缩强度/静态单轴压缩强度)而后再进行对比，如图5(a)所示。可以看出，本研究数据点的趋势线可以较好的表示不同试验数据点的变化趋势。另外，考虑应变率效应，本研究在低应变率范围内进一步与文献[4 - 6, 9, 11, 32]的DIF 结果进行了对比，如图5(b)所示。可以看出，本研究的DIF 数据点基本在不同物理试验的DIF 变化范围内，这进一步验证了上述模拟方法和结果的合理性。

图5 数值模拟值与物理试验值对比Fig.5 Comparison of numerical and test results

3 混凝土双轴压缩强度准则

目前，对于混凝土双轴压-压强度准则，不同学者通过物理试验和数值模拟分别提出或改进了相应的强度准则(如表1)。基于此，本节首先对静态强度准则进行对比，而后对动态强度准则进行验证和讨论。

3.1 静态双轴强度准则

图6 展示了本研究数据点和文献[3, 5, 8 - 9,33 - 41]试验点与规范和“K-G”准则在双轴压-压区内的对比结果。如图6 所示，大部分试验点落在规范和“K-G”准则的强度包络线外，说明规范和“K-G”准则对混凝土材料静态双轴压缩强度的评估相对安全。另外，随着侧应力比逐渐增大，不同试验点的变化趋势与规范和“K-G”准则的强度包络线变化趋势相同。因此，本研究参考文献[2 - 3]，暂时借助已被广泛使用的“K-G”准则的函数形式对数值模拟点进行拟合。该准则的静态双轴压缩强度包络线方程表达式可简化为：

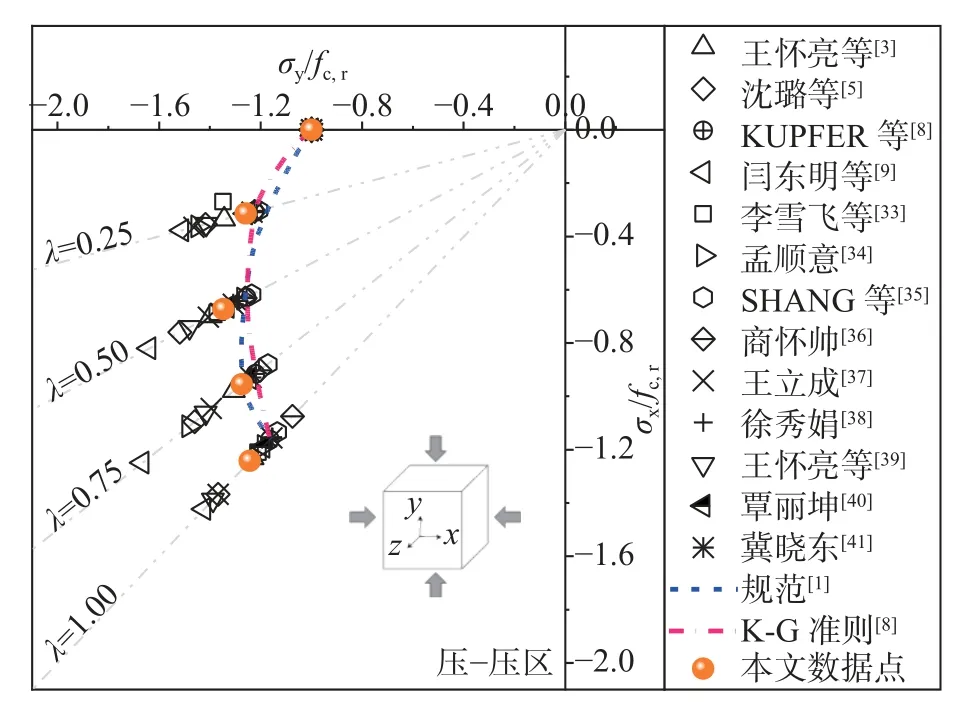
图6 不同静态双轴压缩强度准则的对比Fig.6 Comparison of different static biaxial compression strength criteria

参考式(15)对本研究静态双轴压缩工况下的数值模拟点进行回归分析，可得到参数a= 1，b=3.95。对比K-G 准则的各参数建议取值(a= 1，b=3.65)可知，本研究数值模拟结果是较为准确的。

3.2 动态双轴强度准则

根据2.2 节可知，应变率和侧应力比是影响混凝土动态双轴压缩强度的两个主要因素。本研究首先分别考虑混凝土动态双轴压缩强度与侧应力比和应变率间的关系，而后进行耦合以建立适用于中低应变率下的混凝土强度准则。

3.2.1 侧应力比影响

参考文献[2 - 7, 9]，根据3.1 节的回归分析可知，式(15)可以较好地反映侧应力比对双轴压缩强度的影响。图7 展示了应用不同应变率下的模拟值对式(15)进行回归分析得到的拟合结果。可以看出，在动态双轴工况下，式(15)的应用性相对较好。表3 为不同应变率下的回归分析参数，其中参数a可在不影响式(15)结果的基础上简化为a= 1。至此，可以得到动态双轴压缩强度与侧应力比的关系为：

图7 不同应变率下对式(15)的拟合结果Fig.7 Fitting results of Eq.(15) under different strain rates

表3 不同工况下式(15)的回归分析参数Table 3 Regression parameters of Eq.(15) under different loads

3.2.2 应变率影响

由表1 可知，不同学者考虑应变率对混凝土强度的影响提出了相应的破坏准则。其中，由闫东明和林皋[9]提出的动态破坏准则得到了较多学者的参考和改进[4-7]。但是，受试验设备及条件限制，该准则目前仅在低应变率范围内适用，在更高的应变率范围内是否适用值得研究和讨论。参考文献[4 - 7, 9]，在低应变率研究范围内混凝土动态双轴压缩强度和应变率间的关系为：

首先，本研究在低应变率范围内对式(17)进行验证，如图8 所示。可以看出，在低应变率下，本研究数值模拟点与式(17)吻合良好。

图8 低应变率下数值模拟点与式(17)的拟合结果Fig.8 Fitting results between the numerical data and Eq.(17)under low strain rates

进而，在图8 基础上扩大应变率讨论范围对式(17)进行验证，如图9 所示。可以看出，当应变率增大至中应变率时，式(17)将不再适用。同样地，这也是目前已有混凝土动态双轴压缩强度准则的问题点。针对此，本研究基于已验证过准确性的试验数据，考虑应变率与混凝土动态双轴强度的正比关系，提出以下关系式来表达中低应变率范围内混凝土动态双轴压缩强度和应变率间的关系：

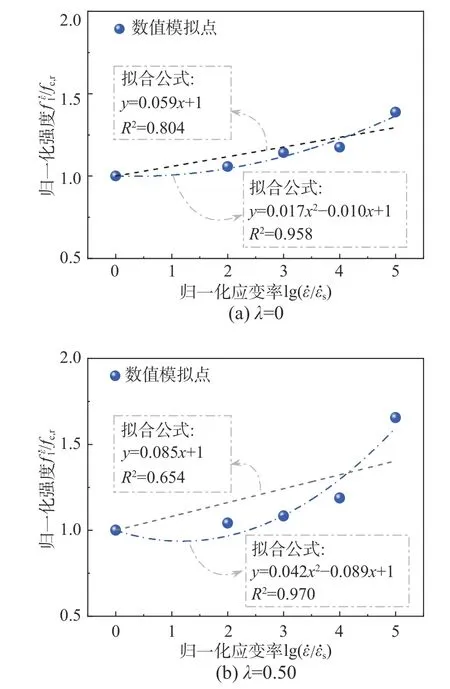
图9 不同侧应力比下对式(17)的拟合结果Fig.9 Fitting results of Eq.(17) under different lateral stress ratios

式中，m、n和w为回归参数。

图9 展示了不同应力比下，本研究数值模拟点分别与式(17)和式(18)的拟合结果。可以看出，式(18)拟合结果的精确度高于式(17)。另外，表4 列出了不同侧应力比下对式(18)的拟合结果。以上结果均初步说明了式(18)可以在中低应变率下较为精确地描述应变率对混凝土动态双轴压缩强度的影响。

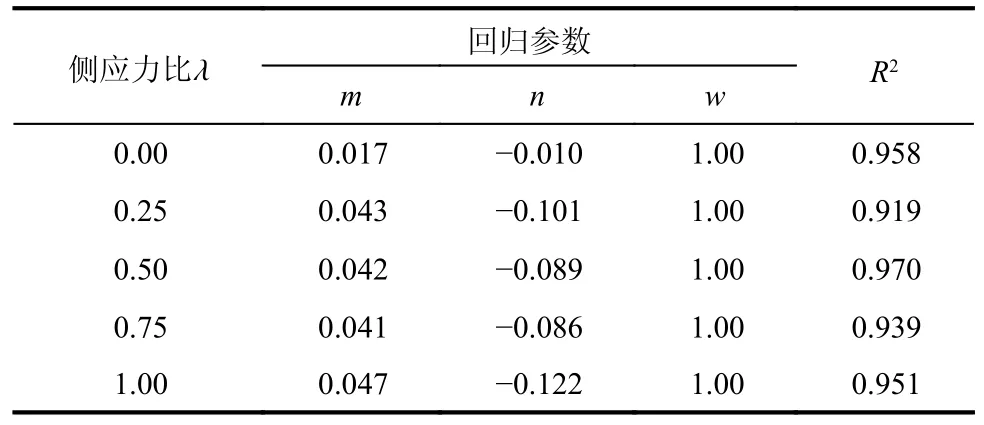
表4 不同侧应力比下对式(18)的拟合结果Table 4 Fitting results of Eq.(18) under different lateral stress ratios

3.2.3 强度准则建立与验证

参考文献[4 - 7, 9]，同时考虑侧应力比和应变率影响，综合式(16)和式(18)即得到动态双轴压-压工况下的混凝土强度准则：

式中，Ph,Pk,Pl,Pm和Pn为拟合参数，1 0-5s-1≤ ε˙≤1 s-1。

为了进一步验证式(19)所提出的混凝土动态双压-压强度准则的准确性和适用性，本研究分别选取了文献[5 - 6]的物理试验数据对式(19)进行拟合，各参数拟合结果如表5 所示。

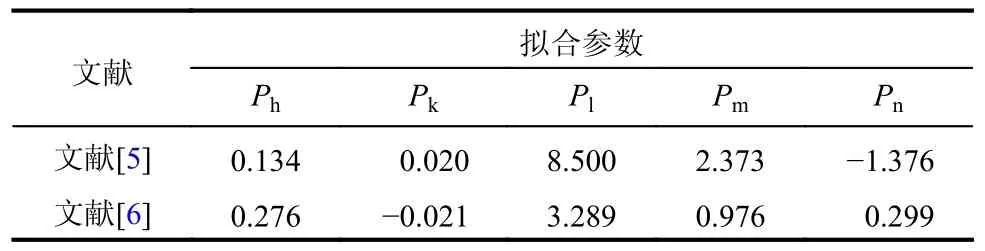
表5 式(19)各参数拟合结果Table 5 Fitting results of parameter in Eq.(19)

另外，图10 和图11 分别展示了应用不同拟合参数得到的混凝土动态双轴强度准则面与文献[5 - 6]的物理试验数据的对比结果。可以看出，在不同应变率和侧应力比下，强度准则面与试验数据点均吻合良好，这进一步验证了本研究建立的动态双轴压-压强度准则的合理性。

图10 强度准则拟合值与文献[5]的对比结果Fig.10 Comparison between the fitted data and Ref.[5]

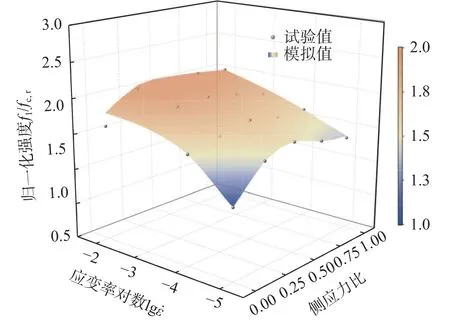
图11 强度准则拟合值与文献[6]的对比结果Fig.11 Comparison between the fitted data and Ref.[6]

4 结论

本文考虑混凝土非均质性，建立了细观随机骨料模型，对尺寸为100 mm 的混凝土立方体试块开展了动态双轴压缩工况下的数值模拟分析，研究了应变率和侧应力比对混凝土破坏模式及压缩强度的影响，初步对适用于更高应变率(10-5s-1≤ε˙≤1 s-1)的混凝土动态双轴强度准则提出了建议。主要研究结论如下：

(1) 相同侧应力比下，随应变率增大，混凝土内部损伤区域增多。相同应变率下，随侧应力增大，混凝土破坏模式由柱状压裂破坏变为片状劈裂破坏。

(2) 混凝土动态压缩强度随应变率增大而增大，随侧应力增大而先增大后减小。不同应变率工况下，双轴强度在侧应力比约为0.5 时达到峰值。

(3) 本研究建议的动态双轴压-压强度准则与已有强度准则相比适用于更高的应变率范围(10-5s-1≤ε˙≤1 s-1)，并且得到了不同物理试验的初步验证。值得说明的是，由于试验条件限制，中高应变率下的混凝土动态双轴压缩物理试验很难开展且试验数据很难收集。因此，本研究暂且只在可收集到的物理试验数据范围内对所提出的混凝土动态双轴压-压强度准则进行了验证。