考虑弹性压缩的弹性支承抛物线拱内力解析解
李双蓓,梁 睿,梅国雄,3
(1.广西大学土木建筑工程学院,广西,南宁 530004;2.广西防灾减灾与工程安全重点实验室,广西,南宁 530004;3.广西大学工程防灾与结构安全教育部重点实验室,广西,南宁 530004)
拱结构在竖向荷载作用下,拱趾支承处除有竖向反力之外,同时存在水平推力,使得拱肋以承受轴向压力为主,大大减小了拱内弯矩,主拱截面的材料强度得到了充分发挥[1-2]。随着我国社会经济的高速发展,工程技术不断提高,拱桥在施工方式和结构形式上不断创新,拱桥跨径不断增大[3-6],拱桥设计与建设的准确性、安全性和经济性对理论解析计算提出了新要求。如今拱桥设计主要运用有限元方法进行数值计算,但对于结构设计分析来说基础解析计算的作用仍不可忽视,有效运用解析计算不仅能够极大提高有限元建模分析的效率,且两者的计算结果可相互校对验证[7]。
平南三桥作为世界第一拱桥,上部超大跨径拱结构导致支座处水平推力达250 920 kN,常规基础结构易产生应力集中导致混凝土拉裂等问题,为此广西路桥集团创造性地提出“拱座、底板-地连墙接触面设置柔性夹层”的新型基础设计方案,以柔性接触代替刚性接触,实际证明这种处理是可靠的。已有研究表明:上部结构的内力性能与基础相互作用。近年来,一些学者开展了基础刚度对上部结构性能影响的研究,范重等[8]研究发现剪力墙结构桩基础桩顶反力值随着基础刚度的增大而增大,且改变基础刚度将导致楼层剪力、结构振动响应、侧向位移等产生显著变化,进而影响结构抗震性能;闫宇智等[9]在对高速铁路简支梁桥行车安全性的影响因素研究中指出基础刚度下降引起的梁桥损伤程度达到90%以上时,将严重影响列车安全;DI 和FU[10]对地震损伤产生的基础刚度退化导致的上部结构内力显著重分布进行了研究,指出基础近部框架柱的剪力和弯矩变化幅度最大;牟在根等[11]在超大跨结构抗震性能研究中指出多点地震激励对结构内力和层间位移转角的影响受基础刚度的影响显著。可见,基础刚度的变化将对上部结构的力学性能产生较大影响,目前的相关研究大多是在建筑结构领域,对桥梁结构与基础相互作用研究方面较少。伴随着拱趾变位等问题的发生,必然导致上部拱结构内力重分布,从而影响拱桥的安全性与耐久性,因此,有必要对采用柔性接触降低基础刚度后上部超大跨桥梁结构的受力进行深入研究。
从力学角度来看,拱座与基础之间以柔性接触代替刚性接触为以理想边界代替非理想边界。近年来,众多学者对理想边界和非理想边界条件下的上部拱结构进行了理论研究,其中非理想边界通过简化为具有一定刚度的弹性支承约束,但研究方向主要集中在稳定承载力[12-19]、动力响应[20-24]和温度-位移响应[25]等方面,而关于非理想边界拱结构基本内力理论解的研究相对空白。特殊基础对拱轴力学性能的影响研究中,除了采用简化的弹性支承约束模型外,另一部分学者则将外部条件引起的拱趾变位作为主动荷载,直接施加在拱趾进行研究[26-27]。
对于跨径较小且矢跨比较大的拱桥通常可不计轴向弹性压缩的影响[28-29],但是部分学者的研究表明:轴力引起的弹性压缩对计算的精确性具有不可忽略的影响。李新平等[30]采用弹性中心法推导无铰抛物线拱的精确内力计算公式,发现在集中荷载作用下不考虑拱肋弹性压缩影响导致计算推力的误差可以达到30%;周宇等[31]基于Ritter公式推导了变截面悬链线无铰拱应变影响线解析解,发现考虑轴力与否的计算偏差随着矢跨比的减少而增大,矢跨比为1/7 时最大偏差大于9%。一些学者则从近似积分的角度对拱结构的解析解进行研究,杨雨厚等[7]基于弹性中心法,采用悬索线近似拟合抛物线的方法推导了具有较高工程精度的抛物线无铰拱挠度影响线实用解析公式;胡长福等[32-34]分别基于弹性中心法和MEXE 方法推导了不考虑轴向压缩和考虑轴向压缩两种情况下的等截面抛物线拱内力实用解析解,并采用悬索线弧长微分近似代替悬链线弧长微分推导了考虑轴向压缩时的等截面悬链线拱内力解析解。此外,丁庆洋[35]基于弹性中心法推导得到抛物线无铰拱在不同工况下的内力解析解,进一步对复杂工况下带悬臂梁的梁拱组合拱结构进行详细求解及参数分析。可见,基本拱结构内力解析解是梁拱组合桥等复杂结构研究的重要基础。
综上研究现状和研究成果,本文将非理想边界约束处理为具有一定刚度的弹性支承约束,在直角坐标系下,基于弹性中心[28]简化体系下的正则方程,采用精确曲线积分,推导了考虑弹性压缩影响的弹性支承抛物线拱精确内力解析解,其中,刚臂长度、常变位和载变位可以显式表达。通过不同矢跨比下的抛物线拱典型截面的有限元解进行验证。从拱结构在竖向荷载作用下支承处产生强大水平推力这一受力特性出发,基于本文的显式解进一步分析了弯压刚度比、弹性柔度系数、矢跨比对水平推力的影响以及弹性柔度系数对拱轴内力分布的影响,为非理想边界拱桥设计计算提供理论支持和新的研究思路。
1 内力解析解
1.1 推导思路
竖向移动荷载作用下等截面弹性支承抛物线拱的计算简图如图1 所示。利用力法将非理想边界拱分成左右对称的悬臂拱,如图2 所示,弹性支承的刚度系数为ki(i=1,2,3),跨中赘余力为xi(i=1,2,3),采用弹性中心简化体系将力法方程简化为易于求解的正则方程,刚臂长度为yS,设竖向移动荷载P的坐标为xP。抛物线拱轴方程为:

图1 抛物线拱计算简图Fig.1 Calculation sketch of parabolic arch
图2 弹性中心法基本体系Fig.2 Basic system of elastic center method
式中:l为跨径;f为拱肋矢高。
为便于计算,令l1=l/2,a=4f/l,并取相对坐标ξ=x/l1,则拱轴方程转化为y=fξ2, ξP为移动荷载相对坐标。拱轴微分关系与水平夹角有如下关系:
经过上述坐标转换后可得如图3 所示基本体系,对应力法方程为:

图3 坐标转换后的弹性中心法基本体系Fig.3 Basic system of elastic center method after coordinate transformation
式中, δij为常变位、 ΔiP为载变位,分别表示基本结构在单位力或单位外荷载单独作用下弹性中心沿xj方向的位移。
基本结构中弹性中心的位移由拱轴变形和弹性支承变形两方面构成,因此考虑拱肋弹性压缩时, δij和 ΔiP基本表达式为:
式中:Mi、Ni、Ri和MP、NP、RP分别为基本结构在赘余力和单位荷载单独作用下的截面弯矩、轴力和支座反力,其中支座反力包括水平、竖向反力和反力矩;EI、EA分别为拱轴截面抗弯刚度和抗拉压刚度,弯压刚度比b=EI/EA;ζ 为弹性支承的无量纲化弹性柔度系数,形式如下:
式中,i=1 时n取1,i=2、3 时n取3。
考虑两侧弹性支承对称设置,基本结构为对称结构,由于赘余力x1和x2正对称,x3反对称,故副系数 δ13、 δ23均为0。而 δ12表达式为:
式中,令 δ12=δ21=0 ,即可求得刚臂长度yS。
基于上述弹性中心法简化体系,式(4)可简化为正则方程:
1.2 基本结构内力及赘余力计算
基本结构内力计算是求解超静定结构内力影响线的基础,表1 给出了赘余力、外荷载单独作用下基本结构的内力,并将其代入式(5)~式(8)进行精确曲线积分后得到考虑拱肋弹性压缩时,计算刚臂长度、常变位及载变位解析解的显式解,如表2 所示。

表1 赘余力和单位外荷载作用下基本结构的内力Table 1 Superfluous force and internal forces under the effect of redundant forces or unit external load

表2 刚臂长度、常变位及载变位显式解Table 2 Explicit solution of rigid arm length, constant displacement and load displacement
表2 中CSi、Ci、CiP和DiP均 为 常 系 数,计 算式如下:
式(21)中,当 ξP=0 时 , β2=0。
将表2 中的 δii、 ΔiP计算式代入正则方程式(9)即可获得赘余力,表达式如式(22)所示:
1.3 内力计算
弹性支承抛物线拱可看作是在外荷载和赘余力共同作用下的两根悬臂曲拱,按照叠加法得到拱轴内力,根据竖向移动荷载作用位置不同,其表达式分别为式(23)~式(25)和式(26)~式(28),将式(22)计算所得的赘余力代入其中即可得到任意截面的内力,拱轴内力表达式根据移动荷载作用在拱轴的位置分为正负半轴两种情况。
当移动荷载位于正半轴即 0≤ξP≤1时,拱轴内力表达式为:
当移动荷载位于负半轴即 - 1 <ξP<0时,拱轴内力表达式为:
式中,弹性柔度系数 ζi为0 时,拱趾弹性支承的刚度趋于无穷大,可得到无铰拱的赘余力和内力解析解,且当 ξP=0时可得到与文献[30]拱顶集中荷载作用下一致的赘余力显式解和内力解析解。
2 算例分析
2.1 解析解公式验证
为验证内力影响线解析解的准确性,以等截面抛物线无铰拱为例,通过Ansys 建立有限元模型,对比所推导的内力计算结果,并比较解析解与有限元解的相对误差。抛物线拱跨径均取575 m,矢跨比分别为1/4、1/4.8、1/5、1/6,拱轴截面抗弯刚度为146.669×106kN·m2,抗拉压刚度为76.158×106kN,1/4、1/5、1/6 三种矢跨比的无铰拱在单位外荷载作用下典型截面内力结果列于表3。图4 表明:矢跨比为1/4.8 时,不同荷载作用位置下本文解析解与有限元计算结果的对比。
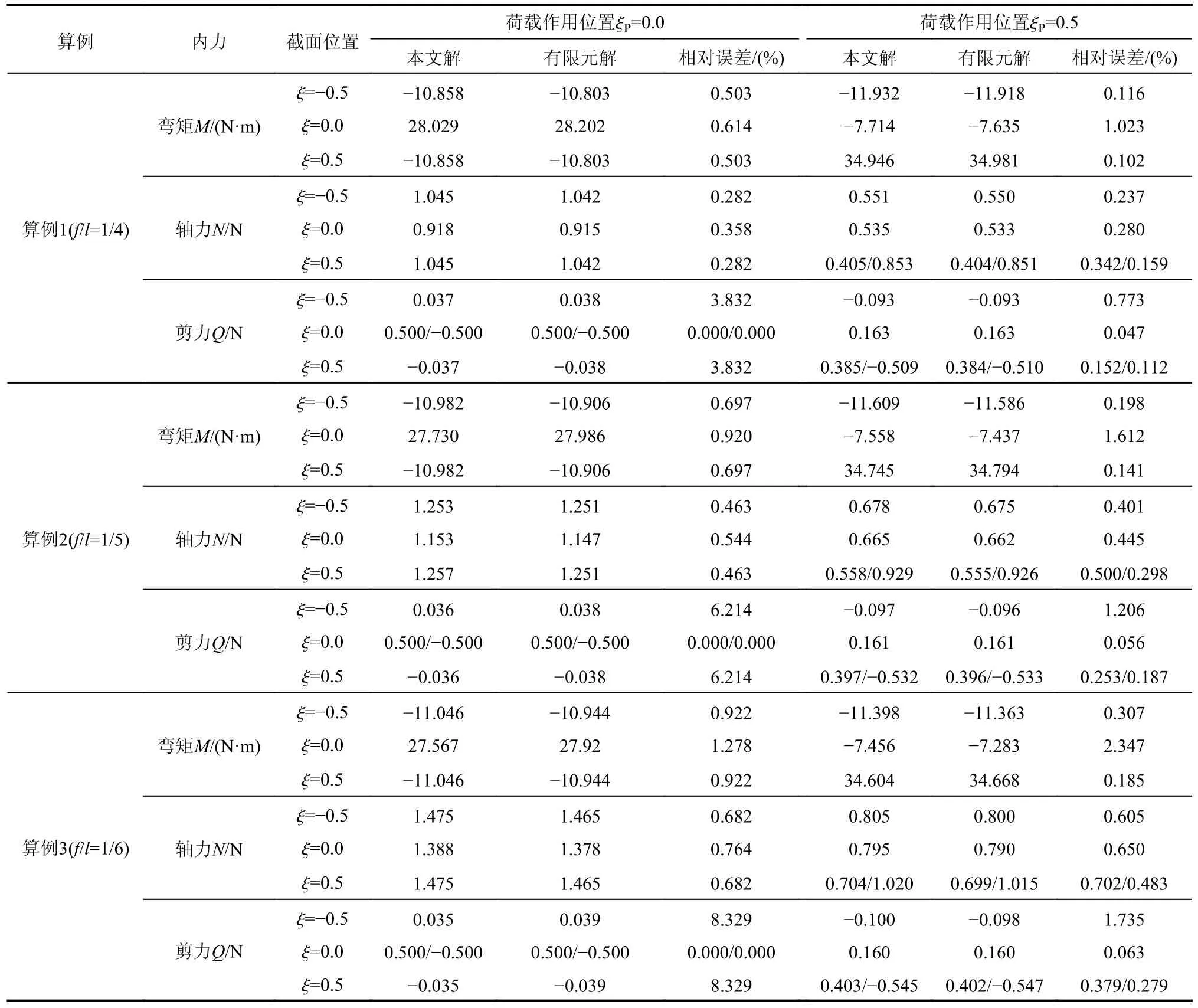
表3 典型截面数值对比表Table 3 Comparison of results of typical sections
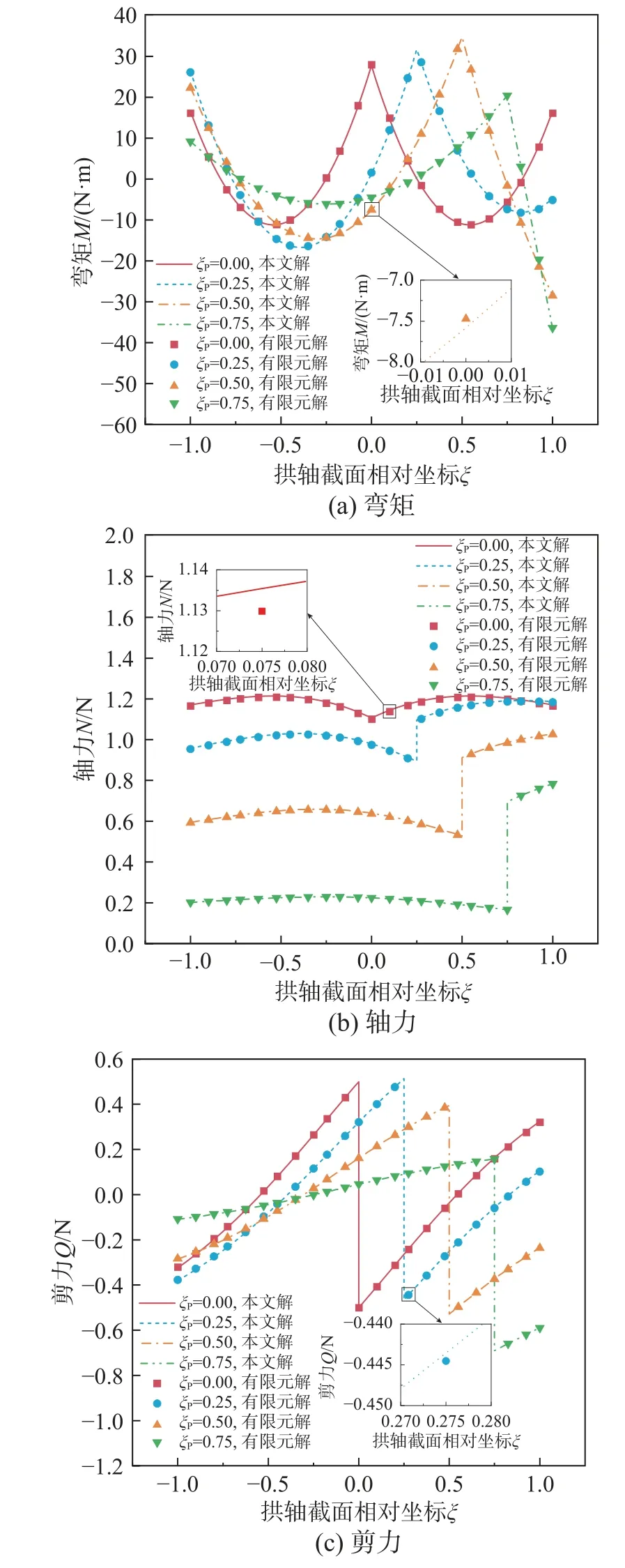
图4 不同荷载作用位置的内力分布图(f/l=1/4.8)Fig.4 Distribution of internal forces at different loading positions (f/l=1/4.8)
由表3 和图4 分析可知,竖向集中荷载工况下,对不同矢跨比的拱轴,本文解析解与有限元计算结果相对误差随矢跨比的减小而增大。轴力的相对误差在1%以内,最大相对误差发生在荷载作用处;弯矩的相对误差在3%以内,最大相对误差发生在拱顶处;荷载作用在拱顶时,跨径四等分截面的剪力相对误差较大且最大达8.329%,但最大绝对误差仅为0.004,该截面位于剪力值零点附近,主要是有限元建模单元以直代曲导致的结果,其他截面的相对误差均在2%以内。解析解与有限元解的内力曲线拟合度高。
2.2 水平推力的影响分析
在竖向荷载作用下,梁在支承处仅受到竖向反力作用,而拱在竖向荷载作用下,支承处还受到水平推力的作用[1],拱结构的这一特性决定了拱结构的支承不仅需要提供与其他结构一样的竖向约束,还需提供水平方向的约束,以抵抗水平推力的作用。 ξP=0表示水平弹性支承抛物线拱在承受拱顶承受集中荷载时的工况,将 ξP=0代入表2可得到该工况下刚臂长度yS显式解,如式(29)所示,同样可得到常变位 δ22和载变位 Δ2P的显式解,并将其代入式(22)所示正则方程得到赘余力x2的显式解,而水平推力H和赘余力x2大小相等,故水平推力H的显式解如式(29)和式(30)所示。
式中, ψ为拱顶集中荷载作用下的水平推力影响系数,表达式为:
针对拱结构受力特性所需的构造要求,以拱顶承受集中荷载的水平弹性支承抛物线拱为例,运用显式解进一步分析弯压刚度比b、弹性柔度系数ζ2、矢跨比f/l对水平推力影响系数的影响,算例跨径为575 m,水平推力影响系数的变化曲线如图5 所示。
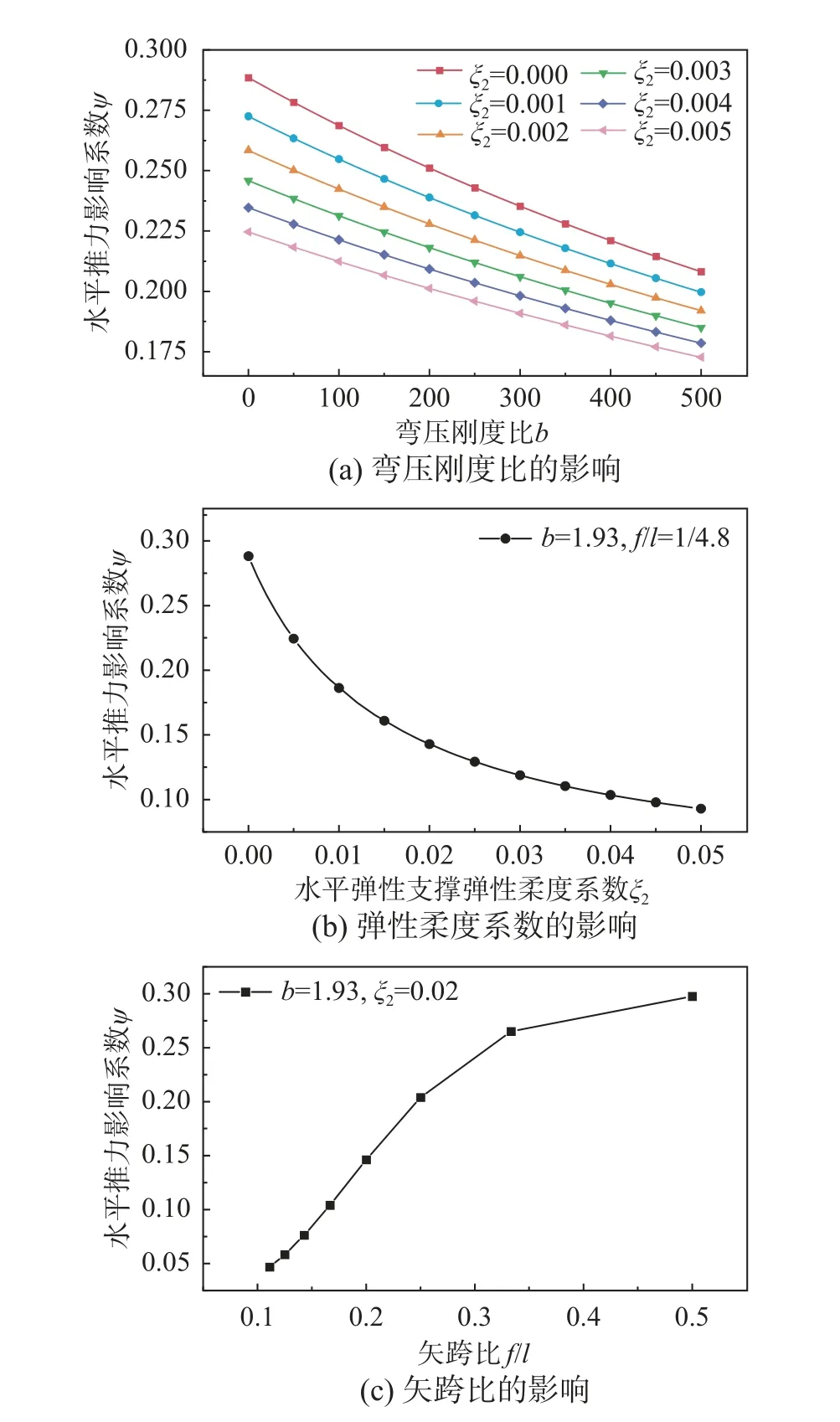
图5 不同参数影响下水平推力影响系数ψ 的变化曲线Fig.5 Variation curve of influence coefficient of horizontal thrust ψ under different parameters
图5(a)为水平推力影响系数随弯压刚度比的变化曲线。从图5(a)中可见,随着弯压刚度比的增大,水平推力影响系数呈近似线性减小,且减小趋势随水平弹性支承弹性柔度系数的增大而减弱,说明在支承处设置水平弹性弹簧有利于减弱弯压刚度比对水平推力影响系数的影响。当弯压刚度趋于无穷大时,为不考虑拱肋弹性压缩的影响,对于弹性柔度系数为0 即无铰拱,弯压刚度比为1.93 时水平推力影响系数为0.288,弯压刚度比达到500 时水平推力影响系数减小到0.208,即若不考虑拱肋的弹性压缩影响可能导致水平推力的计算误差可以达到27.8%。
图5(b)给出了矢跨比为1/4.8、弯压刚度比为1.93 时,水平推力影响系数随弹性柔度系数的变化曲线。从图5(b)中可见,随着弹性柔度系数的增大,水平推力影响系数呈非线性减小,减小趋势先急后缓。弹性柔度系数从0 增大到0.01,水平推力影响系数减小了约0.1,减小幅度约35.34%;当弹性柔度系数增至0.02 后,曲线下降明显变缓。
图5(c)为弯压刚度比为1.93、弹性柔度系数为0.02 时,水平推力影响系数随矢跨比的变化曲线。从图5(c)中可见,当矢跨比小于1/3 时,水平推力影响系数随着矢跨比的增大呈接近线形增大;当矢跨比大于1/3 时,水平推力影响系数随着矢跨比的增大逐渐趋于稳定。对于常见矢跨比的抛物线拱,水平推力影响系数在0.15 左右。
上述分析表明:在拱顶竖向集中荷载下,忽略拱肋弹性压缩对拱的水平推力影响很大,弯压刚度比越大误差越大。在支承处设置水平弹性弹簧不仅有利于削弱拱肋弹性压缩对水平推力影响系数的影响,还能对水平推力的大小起到显著的调控作用。
2.3 水平弹性支承对内力的影响分析
随着水平弹性支承弹性柔度系数的变化,支承处的水平推力发生显著改变,拱轴内力必然也将随之变化,下面分析水平弹性支承抛物线拱在承受拱顶承受集中荷载时,弯矩M、轴力N和剪力Q随弹性柔度系数变化的规律。拱轴的跨径和截面参数与2.1 节相同,矢跨比为1/4.8。图6 为抛物线拱在不同弹性柔度水平弹性支承时的拱轴内力分布图。图7 为抛物线拱在拱趾、荷载作用处和极值截面三个典型截面的内力之比随水平弹性支承柔度系数的变化曲线,将此内力之比称为内力特征值,即弯矩、轴力和剪力的特征值分别为M/M0、N/N0、Q/Q0,其中M0、N0、Q0为对应柔度系数 ζ2为0 即无铰拱时的典型截面内力。
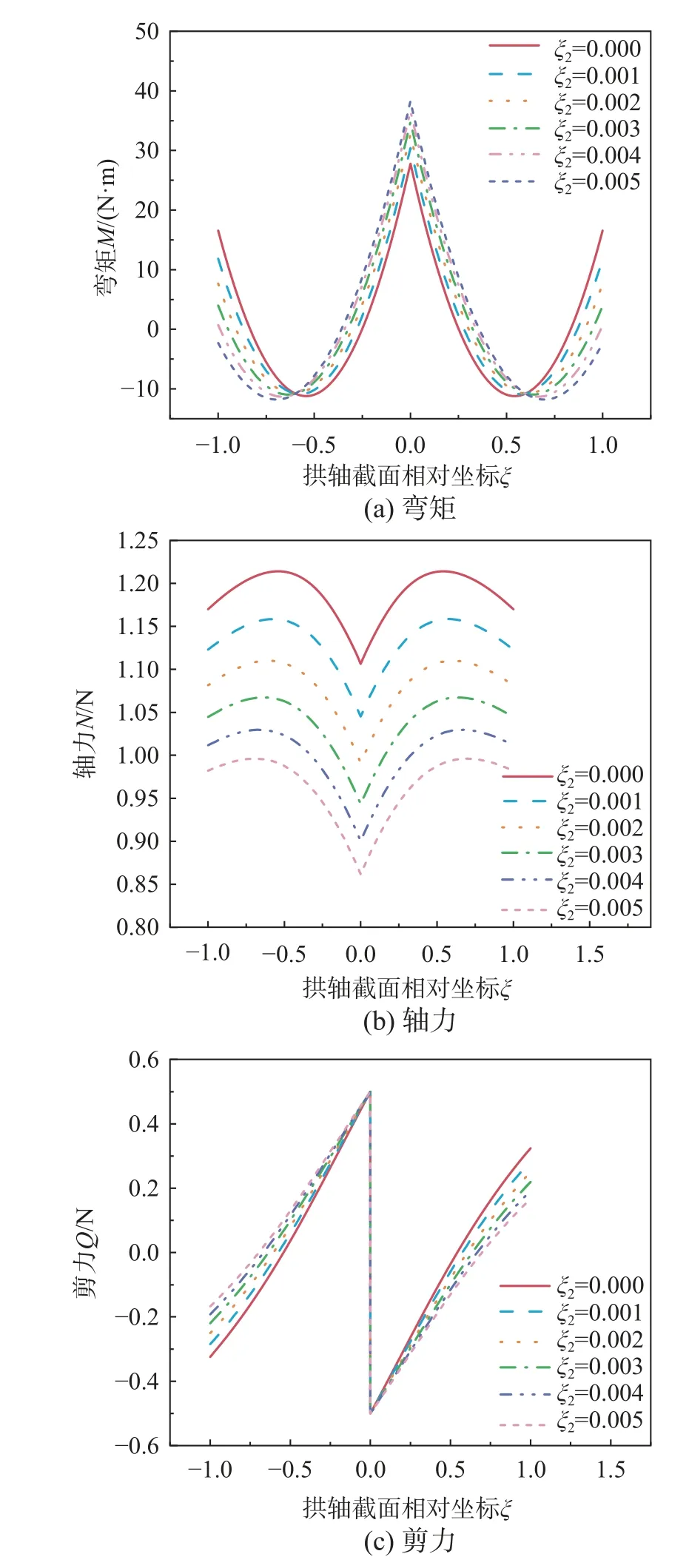
图6 不同柔度系数水平弹性支承抛物线拱内力分布图Fig.6 Distribution of internal forces of parabolic arches with different flexibility coefficients of horizontal elastic supports
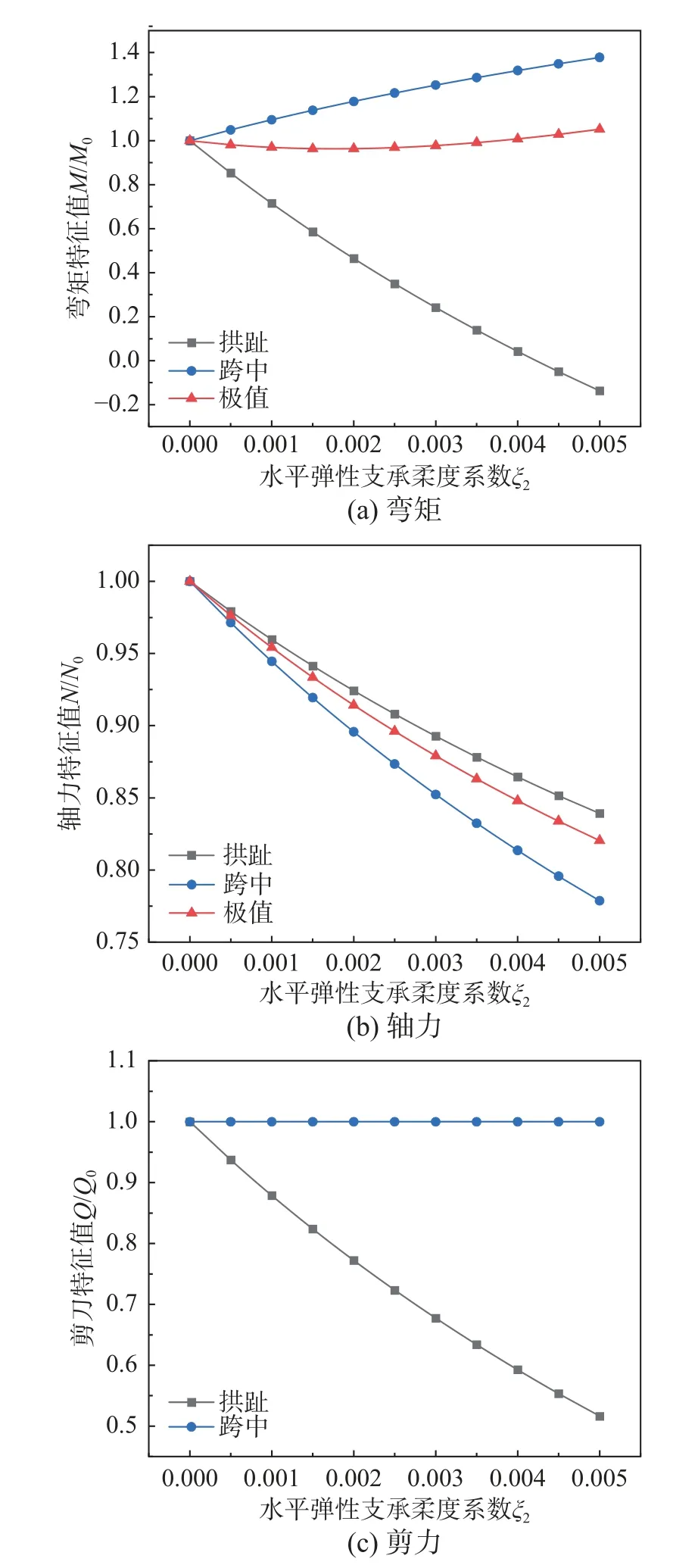
图7 内力特征值随水平弹性支承柔度变化曲线Fig.7 Variation curve of internal force characteristic value with flexibility coefficient of horizontal elastic support
从图6 和图7 可见随着柔度系数的增大,拱趾附近弯矩的变化幅度最大,且弯矩值出现变号,所以随着柔度系数的增大,拱趾附近弯矩会先减小后增大;跨中区域弯矩随着柔度系数的增大而增大,增幅最大发生在跨中截面;弯矩极值变化幅度最小。拱内各点的轴力随着柔度系数的增大而减小,沿跨径来看,跨中轴力的减小幅度最大,越靠近拱脚轴力的减小幅度越小,极值的减小幅度略低于跨中轴力。柔度系数对剪力的影响程度沿跨中至拱趾呈增大趋势,拱趾处最大。跨中至剪力零点截面的剪力随着柔度系数的增大而增大,剪力零点截面至拱趾段的剪力变化相反,拱趾处的变化幅度最大。可见,水平弹性支承对拱轴内力具有显著的调控作用,并且随着水平弹性支承柔度系数改变,内力发生不同程度的改变,弯矩的变化幅度最大,其次是剪力,轴力的变化幅度最小。
3 结论
本文将非理想边界简化为弹性支承,采用精确曲线积分推导得到考虑弹性压缩的刚臂长度、常变位和载变位显式解和拱轴内力解析解。通过与有限元解比较,证明本文解析解正确可靠。可准确高效对竖向移动荷载作用下等截面弹性支承抛物线拱进行内力理论计算与分析,并得到如下结论:
(1) 在拱顶竖向集中荷载下,不考虑拱肋弹性压缩影响导致的水平推力计算误差最大发生在拱趾支承为刚性约束时,最大误差可以达到27.8%,且弯压刚度越大误差越大;支承处设置水平弹性弹簧可以削弱拱肋弹性压缩对水平推力计算误差的影响,并且对水平推力具有显著的削弱作用;水平推力影响系数随矢跨比的增大而增大,弯压刚度比为1.93、水平弹性支撑柔度系数为0.02 时,常见矢跨比的抛物线拱水平推力影响系数在0.15左右。
(2) 水平弹性支承对抛物线拱的拱轴内力分布具有显著的调控作用,尤其是随弹性支承柔度系数的增大,拱趾附近的内力削弱幅度最大;随着水平弹性支承柔度系数改变,内力变化幅度大小依次为弯矩、剪力和轴力。
本文研究成果可为拱肋与支承基础协调设计及其优化提供参考。

