基于视觉和振动监测数据融合的结构动态位移识别及其试验验证

修 晟，张 愿，单伽锃,2

(1.同济大学土木工程学院结构防灾减灾工程系，上海 200092；2.上海韧性城市与智能防灾工程技术研究中心，上海 200092)

目前，我国土木工程领域事故时有发生，如桥梁的骤然断裂、房屋的突然倒塌等，造成重大的人员伤亡以及财物损失。作为评估工程结构的手段，结构健康监测逐渐成为土木工程的重要研究领域之一[1-2]。进行结构健康监测时，系统识别是分析潜在损伤的重要环节。为了实现系统识别，需要利用传感器对加速度、位移等结构响应进行测量[3]。这类信息可以反映结构的完整性，判断结构状态，在使用中的极端值可能显示负载异常或结构缺陷[4-5]。此外，也可以用位移监测的结果对结构的有限单元模型更新[6]。

结构工程领域有许多手段可以直接测量结构的位移响应，这些手段包括拉线式位移计、线性可变差动变压器 (LVDT)、实时动态全球卫星导航系统(RTK-GNSS)等[7]。LVDT 通常需要安装在目标点和固定参考点之间，因此尽管LVDT 测量精度高，但实际工程中安装不便。RTK-GNSS 比一般的GNSS 精度高，但是采样频率低[8]。加速度二次积分也被用来测量位移，但这种方法存在低频漂移现象。已有许多方法用于解决漂移问题，但这些方法也会移除结构在低频的响应信息[9]。

近几年来光学相机、光学镜头迅速发展，基于计算机视觉的结构监测与检测逐渐成为热点[1,10]，其主要应用领域包括结构裂缝识别[11-12]、融合其他传感器数据的结构影响线计算[13]、结构动力响应测量[14]和结构振动模态测量[15-16]等。基于计算机视觉的动态测量方法具有测量精度高、距离远、成本低、能实现整体测量等优点[2,11]。相机可以捕捉结构运动，并对图像处理来测量结构的位移，但位移精度很大程度上受到光照条件和分辨率的限制。此外，现有数码相机大多只有较低的帧率，无法收集高频信息，并且高频位移振幅较小，难以识别[17]。对此，可以通过融合加速度传感器数据解决上述问题[2]。

1 结构位移视觉识别

通过计算机视觉识别结构位移的一般过程如下[18]：首先，为减小计算量，并提高计算精度，需要选取目标区域(region of interest, ROI)。随后，在选定的ROI 范围内寻找特征点。计算机视觉位移监测中，需要将人工标志或自然标志置于ROI之内。自然标志是指已有的结构目标，如天然裂缝；而人工标志则是专门用来测量位移的标志，这些标志可以看作特征。有多种方法可以计算特征点，如Harris 角点、SIFT 点以及SURF 方法等[9]。之后，通过特征匹配方法，如暴力搜索算法和BBF搜索算法等，对第j帧的特征点和第一帧的特征点进行匹配。匹配的结果需要通过随机抽样一致法(RANSAC)等方法，将异常点剔除。计算第j帧和第一帧的相对位移时，可按以下方法计算[19]：

式中：N为匹配结果数；di为以像素为单位的结构相对位移。最后，通过比例因子将测得的像素位移转换到实际位移。

式中，α 为比例因子，可通过以下公式进行估计[20]：

式中，ut和dt分别表示人工和自然标志物的相应的物理尺寸和像素尺寸。

2 加速度和位移的数据融合

2.1 比例因子计算

计算机视觉测量得到的是为以像素为单位的位移，为了获得实际的位移值，传统的基于视觉的位移测量方法，需要提供额外的尺寸信息，来计算比例因子。这种计算方式需要额外的特征提取过程，而且对边缘识别有更高要求，很容易产生测量误差。此外还存在某些情况下标识的尺寸信息难以测量等问题。利用加速度数据可以估计比例因子，具体流程见图1。

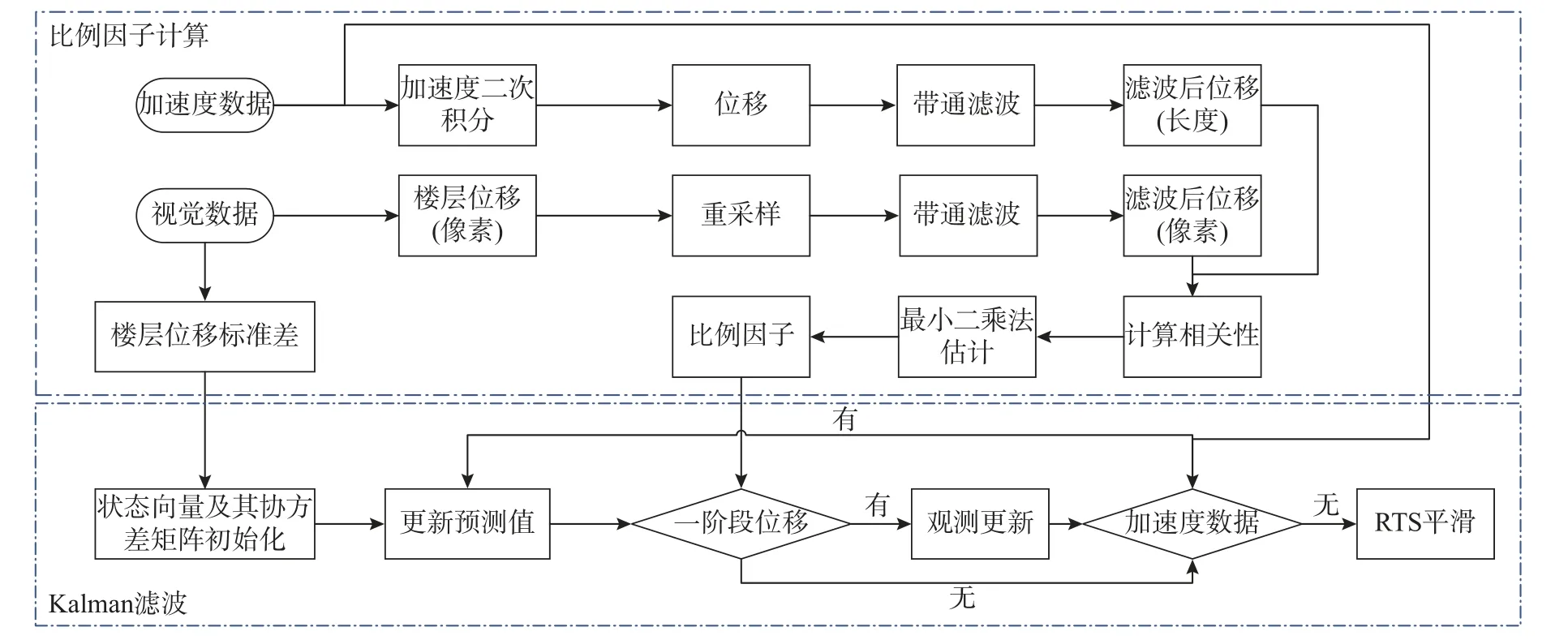
图1 数据融合流程Fig.1 Flow chart of estimate scale factor

该方法首先计算以像素级别的位移，再用加速度二次积分计算结构的位移。为避免加速度传感器的低频漂移现象，积分结果需要经过带通滤波。同时，对视觉测量的结果升采样到与加速度测量相同频率。视觉测量的结果同样需要带通滤波，滤波范围和积分结果相同，以减小滤波范围外的影响。最后，用最小二乘法求出比例因子。

2.2 多速率卡尔曼滤波算法

卡尔曼滤波是一种广泛应用于数据处理的方法，该方法通过在时域上不断预测、修正，对数据进行估计。一般而言，加速度计采样频率高于视频的帧率，即加速度的采样率高于位移测量采样率。对此，SMYTH 和 WU[21]采用多速率卡尔曼滤波器融合不同采样率下的加速度和位移，来改善位移信号的估计。该方法将低采样率的位移数据和高采样率的加速度数据进行数据融合，状态方程如下：

式中：X(t)=[x(t),x˙(t)]T，x(t) ,x˙(t)分别为位移和速度；u(t) 为加速度的观测值； α(t)为状态噪声，α ～N(0,q)，q为加速度方差。

将基于计算机视觉的测量的位移作为观测值，可建立如下的卡尔曼滤波观测方程：

式中， β(t) 为位移观测噪声， β ～N(0,r)，r为位移方差。

上述方程的离散形式可以表示为：

式中：k为时间步；uk和zk分别为测量的加速度和位移数据；wk和vk分别为离散的状态噪声和测量噪声。状态噪声协方差为Q，观测噪声协方差为R。

式(7)中矩阵A、B和H分别为：

式中，dt为加速度采样间隔。

相应的噪声的协方差矩阵可以写成：

融合位移和加速度的多速率卡尔曼滤波流程如图1 所示，具体步骤为：

1) 状态向量及其协方差矩阵初始化。

2) 基于加速度数据的预测。状态预测公式为：

相应的协方差矩阵预测公式为：

3) 当进行τd/τa次预测后，融合加速度和位移数据进行观测更新，式中τd、τa分别代表位移和加速度测量时间间隔。

RTS 平滑是一种固定区间的最优平滑算法，它利用固定时间区间的全部观测值来估计区间每个时刻的状态，具体公式推导见文献[22]。

2.3 位移测量噪声参数估计

如式(2)所述，实际的位移为比例因子和像素位移的乘积。根据误差传递规律，位移测量的方差的可由下式计算：

3 振动台试验

本文以一个大比例钢筋混凝土框架模型振动台试验为例，在模型振动台试验中，结构动力行为识别接近工程实际，对计算机视觉的实际应用具有参考价值。

3.1 试验基本信息

本试验在4 m×4 m 三向6 自由度地震模拟振动台上进行，振动台最大承重25 t，频率范围为0.1 Hz～50 Hz，最大位移±100 mm，最大速度±1000 mm/s，台面最大加速度X向±4g、Y向±2g、Z向±4.0g。框架结构柱截面均为 125 mm×125 mm，框架梁的截面取为70 mm×120 mm，楼板厚度均为35 mm。

结构模型上设置有红外光学位移测量系统的红外靶点。这套由加拿大NDI 公司开发的 Optotrak®CertusTM 三维运动测量系统，利用3 个CCD 镜头捕捉标识点发射的红外光源，测量标识点精确的三维空间位置信息，并将此信息传输到系统控制单元进行处理。模型上另设有10 个加速度计。使用 SONY HDR-PJ220E 高清摄像机以斜视角度拍摄框架结构振动试验视频数据。拍摄的视频分辨率为1920×1080，色深8bit，拍摄时选取的帧速率为25 帧/秒。最终结果以红外系统测量数据作为真值。

3.2 试验工况

本试验有3 种地震工况，选用的地震波分别为2011 年日本“3·11”地震波、1994 年Northridge地震波和上海人工波。统一对三种地震波进行调幅，设定地面加速度峰值(PGA)为0.2g。三种地震波具有不同的频谱特性，以激发框架结构不同的地震反应特征。

3.3 试验分析

3.3.1 计算机视觉处理

框架结构视觉追踪的ROI 选择如图2 的蓝色虚框所示。一般的，过大的ROI 选择造成计算成本高，误匹配、错匹配增加；过小的ROI 则无法保证覆盖目标区域移动的全部范围，带来大振幅下特征点匹配适量少和误匹配的问题。ROI 的选择可依据现场光照条件、目标区域构件几何尺寸、整体结构物理特征等确定初始范围，并采取试算法迭代确定最优范围。

图2 大比例RC 框架布局和实景Fig.2 The large-scale RC frame and the region of interest (ROI)

3.3.2 比例因子影响

由于各自设备的限制，本试验中加速度传感器、摄像机红外系统的采样频率分别为256 Hz、25 Hz 和128 Hz。这三种传感器系统各自独立采样，使用不同的时钟，这不仅使得数据难以融合，而且也使得计算效果难以比较。因此，在进行数据融合和比较之前，需要对数据进行预处理。XU 等[23]在对加速度信号和GPS 信号融合时，通过插值和计算互相关系数实现不同信号间的时间同步。考虑卡尔曼滤波算法限制，加速度的采样频率一般设定为视觉采样频率的整数倍，所以本研究将这三类信号统一重采样为250 Hz。插值后，以计算机视觉所测位移序列为基准，加速度二次积分位移序列和红外测量位移序列分别与计算机视觉位移序列计算最大互相关系数(cross correlation)，以此完成不同信号间的时间同步。

本文计算得到的比例因子结果如图3 所示。由图3 数据点沿直线近似分布可知，最小二乘法拟合效果良好。

图3 日本“3·11”地震工况下各层位移/像素的比例因子Fig.3 The regressed scale factor between displacement and pixels for each floor under the Japan ＂3·11＂ excitation scenario

作者已有比例因子计算方法[18]需要在图像中提取框架梁上、下边缘，计算以像素(pixel，单位表示为px)为单位的框架梁高，结合已知结构框架梁高度为0.12 m，计算比例因子。本文的结果与文献方法的结果对比见图4。由此可见，一般情况下，本文使用的比例因子计算方法与作者已有视觉识别方法[18]计算得到的比例因子很接近。但需要注意的是，楼层4 的比例因子差距相对较大。如图2 所示，楼层4 位于图像畸变较大的区域，可能导致单一视觉识别方法出现构件边缘识别的不确定性与差异，进而影响相应楼层4 比例因子计算结果的准确性。

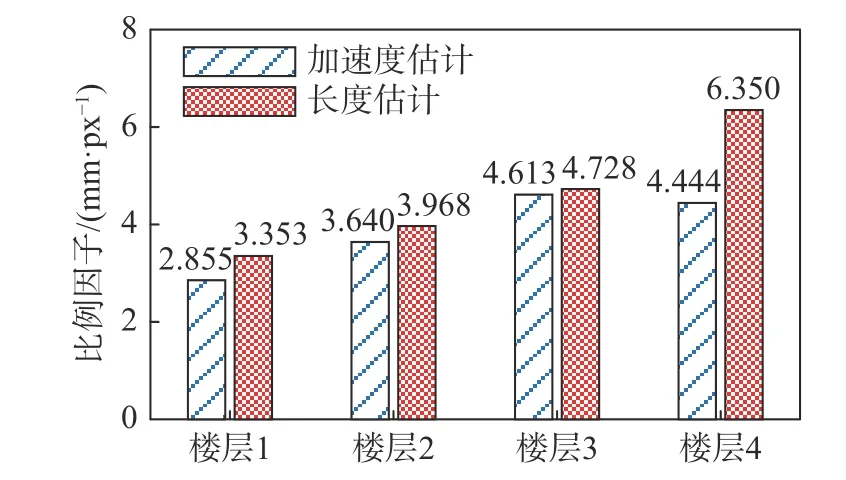
图4 两种方法下日本“3·11”地震工况下各楼层比例因子比较Fig.4 Compare of scale factor under the Japan ＂3·11＂excitation scenario

结构在地震作用下的响应，层间位移角是个重要的物理量。为此，在时域范围内，本文通过以下两个指标来判断结果正确性：

1) 峰值误差，即位移最大处的误差。该指标对最大层间位移角 有重要意义。

2) 归一化均方根误差(normalized root mean square error, NRMSE)，该指标从整体上判断测量误差。其公式定义如下：

式中：xˆi和xi分别代表第i步的估计值和真实值；n代表数据点数目。

日本“3·11”地震工况结果见图5。可以看出，在本工况下，本文方法相较文献方法对比例因子的计算更可靠。

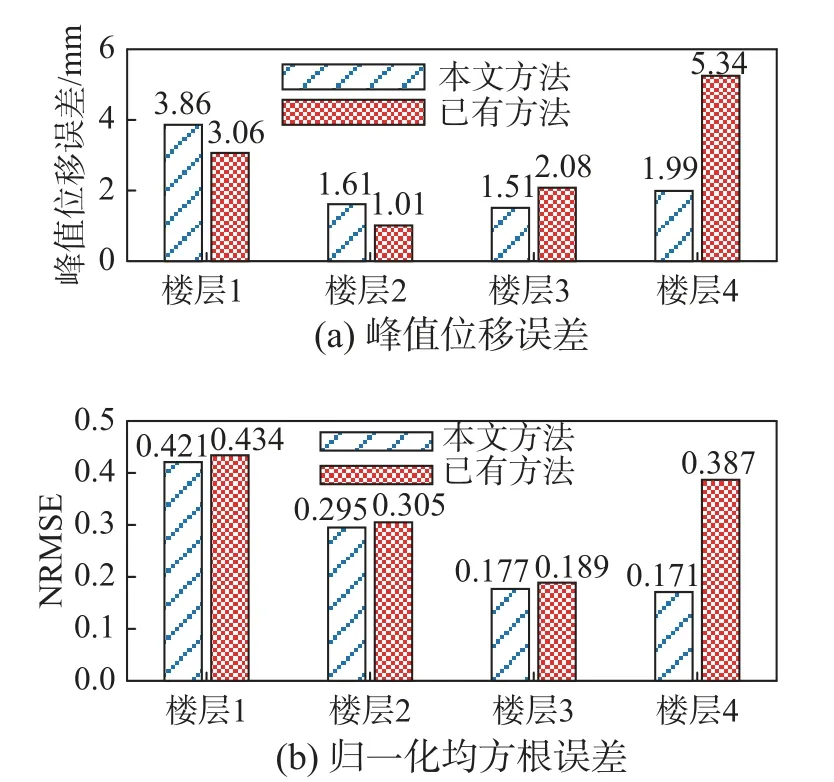
图5 日本“3·11”地震下各层峰值误差和归一化均方根误差Fig.5 Peak error and NRMSE for each floor under the Japan＂3·11＂ excitation scenario

对本实验，在卡尔曼滤波过程中，指定加速度传感器的方差为2×10-2m2/s4，计算机视觉测量的位移方差由式(16)计算。

卡尔曼滤波后，各个工况下时程对比分别如图6～图8 所示。

图6 日本“3·11”地震下各层时程结果对比Fig.6 Time history results for each floor under the Japan＂3·11＂ excitation scenario

图7 Northridge 地震工况下各层时程结果对比Fig.7 Time history results for each floor under the Northridge excitation scenario

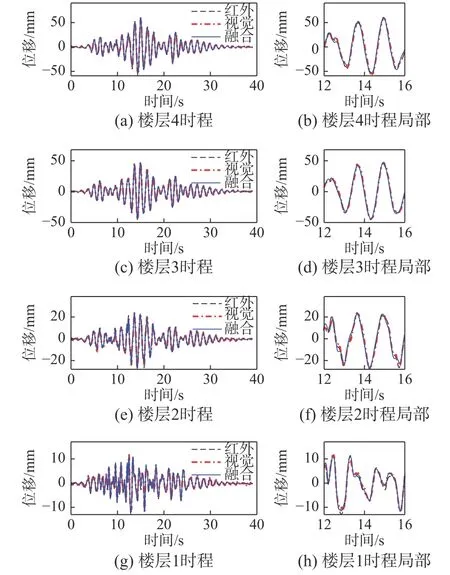
图8 上海人工波工况下各层时程结果对比Fig.8 Time history results for each floor under the Shanghai artificial wave excitation scenario

各个工况下，峰值误差和归一化均方根误差分别见表1 和表2。

表1 峰值误差统计Table 1 Peak error statistics

表2 归一化均方根误差统计Table 2 NRMSE statistics

由表1 可看出，卡尔曼滤波对误差峰值的改进不明显。如果滤波前误差大，则融合之后可减小误差，而如果滤波前误差已经比较小，则该方法对误差峰值的改进不明显。

由表2 可知，NRMSE 更强调整体， 卡尔曼滤波的效果更加明显。除在少部分工况下结果劣化外，大部分工况均有改进，最大幅度达38%。同时注意到，有2 个工况在卡尔曼滤波后出现一定程度的劣化，但基本在9%以内。考虑在相应工况下，基于视觉识别的NRMSE 已经比较小，所以卡尔曼滤波进一步改善的效果不明显。

在频域范围内，功率谱密度(PSD)是识别结构动力特性的一个重要指标。各地震工况下频谱图见图9～图11。

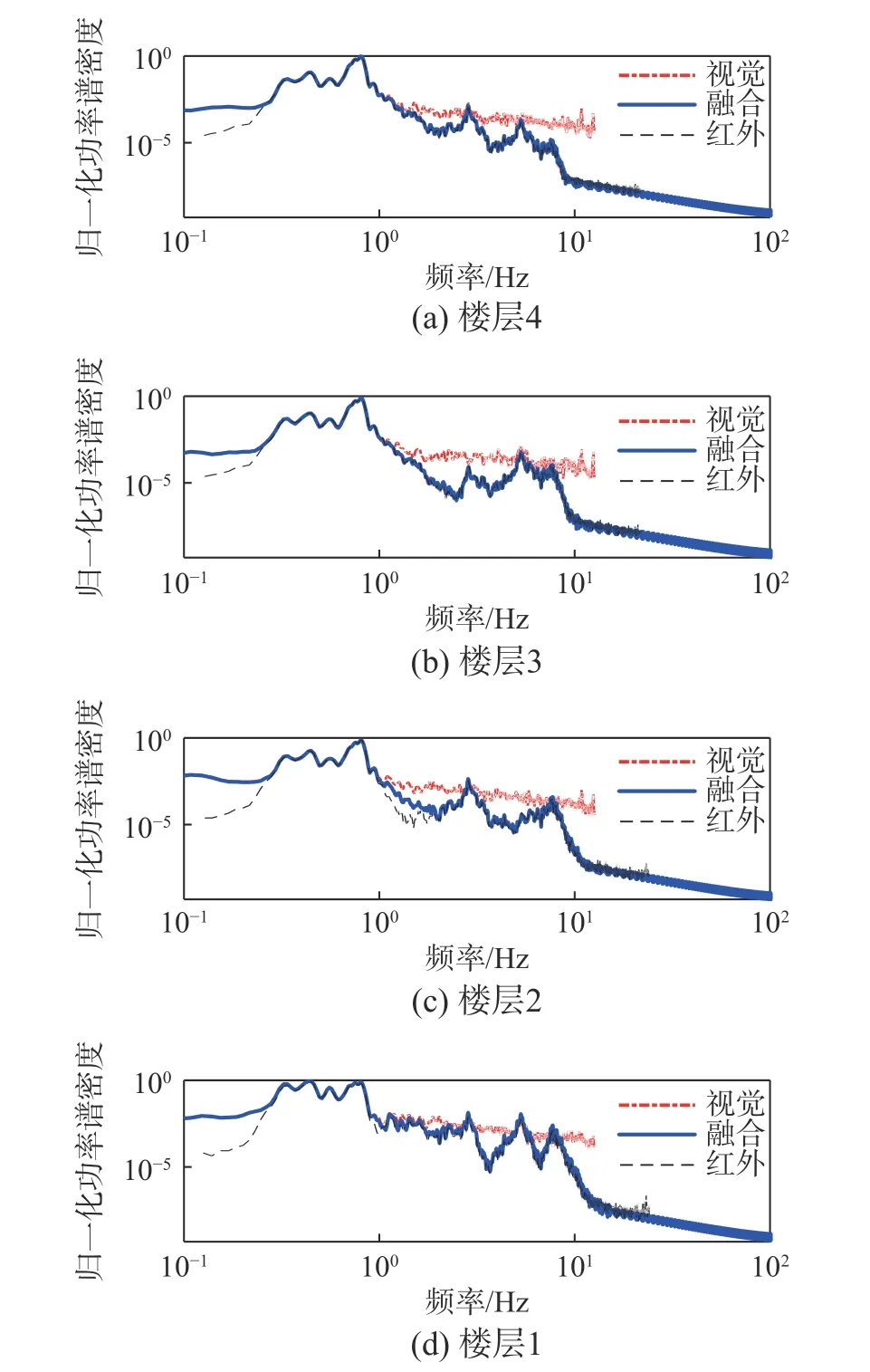
图9 日本“3·11”地震工况下各楼层归一化功率谱密度Fig.9 Normalized PSD for each floor under the Japan ＂3·11＂excitation scenario

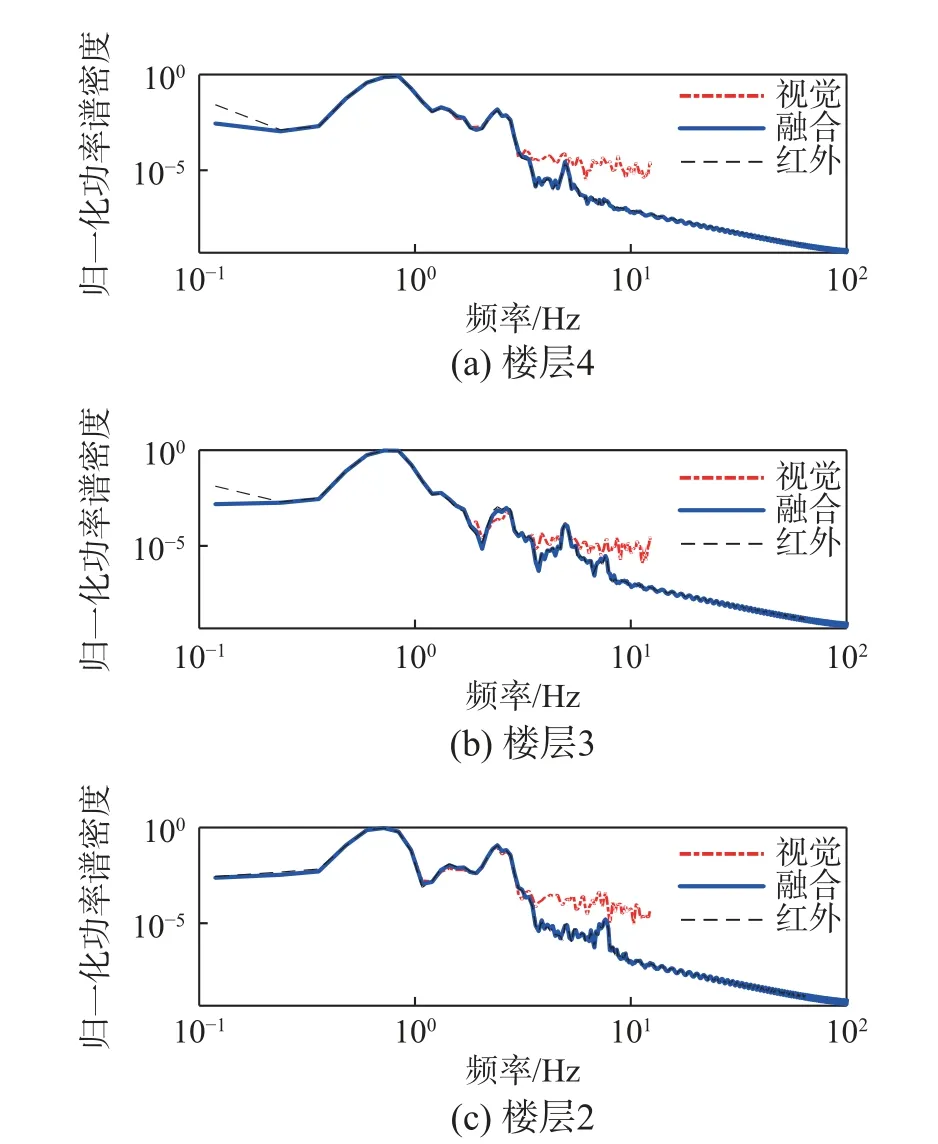
图10 Northridge 地震工况下各楼层归一化功率谱密度Fig.10 Normalized PSD for each floor under the Northridge excitation scenario

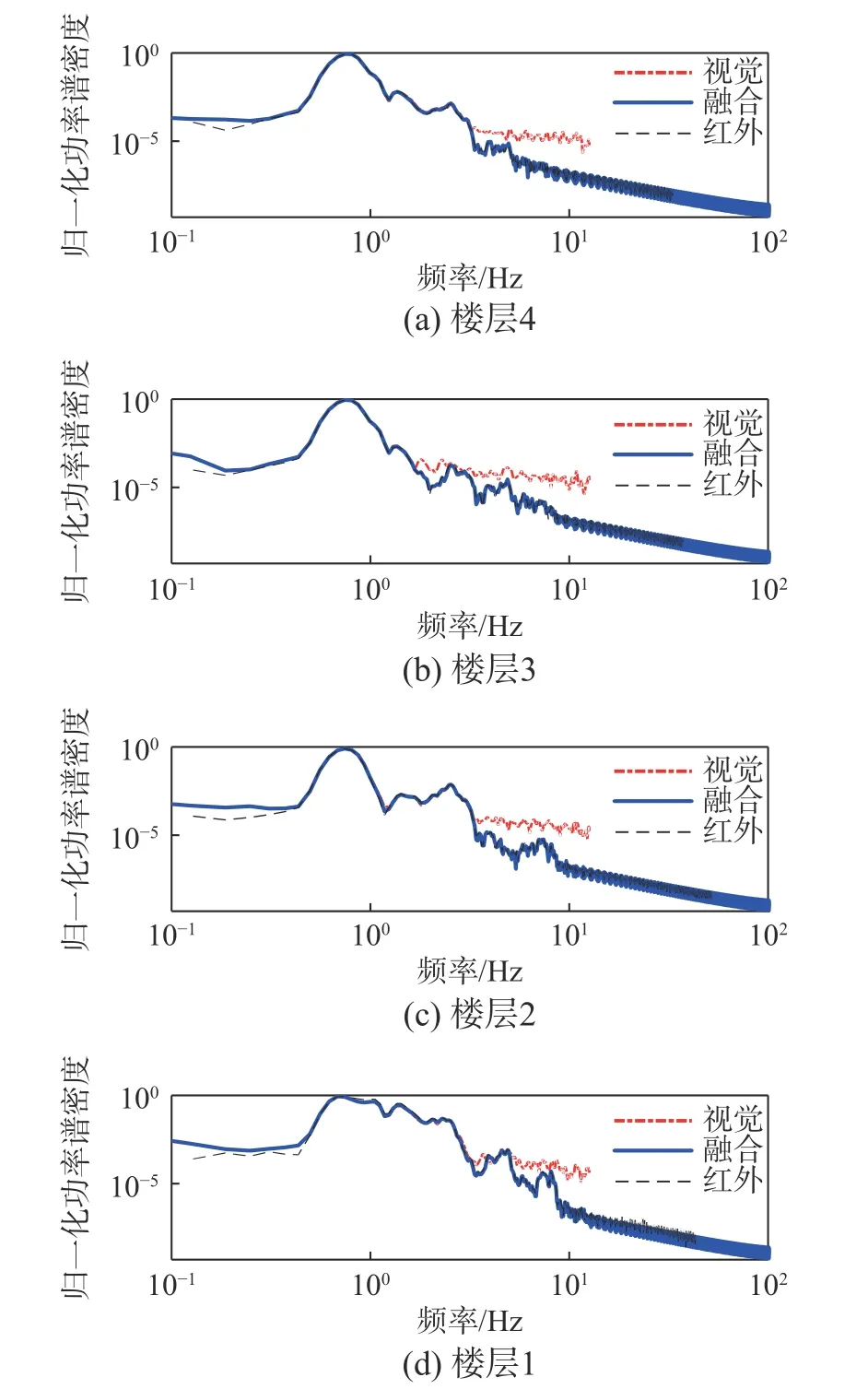
图11 上海人工波工况下各楼层归一化功率谱密度Fig.11 Normalized PSD for each floor under the Shanghai artificial wave excitation scenario

在频域范围内，可以明显看出，卡尔曼滤波后频率更加接近红外系统测量结果。在所有工况下，结构的高频信息都更加接近红外系统结果，这对判断结构的频率和模态均有帮助。对低频部分，卡尔曼滤波后，归一化功率谱密度曲线与纯视觉结果相同。由于日本“3·11”地震工况时间更长，相比其他两个工况，结构的自振频率更突出。

4 结论

本文利用加速度传感器和计算机视觉技术，对结构动力行为的接触式监测和非接触式追踪数据进行融合，以充分发挥两者优势。针对计算机视觉技术无法采集结构高频振动信息，需要额外参数估算比例因子等不足而加速度计无法监测低频位移、存在零漂等缺点，本文提出利用卡尔曼滤波和RTS 平滑方法，用最小二乘法计算比例因子，融合了计算机视觉和加速度计的数据。并以一个大比例框架结构振动台试验为例，验证了方法的可靠性。结果表明：

(1)该种数据融合方法能够可靠估计比例因子；

(2)在时域范围内，虽然对结构最大位移的测量改进不明显，但有效减少了NRMSE 值，整体上提升了位移测量精度；

(3)在频域范围内，所提出的数据融合方法，弥补了纯计算机视觉采样率低的缺点，有效提高了位移数据在高阶模态范围内的信噪比，保证了对结构高阶模态的识别能力。下一步的工作将研究ROI 的选择方法，实现ROI 的自动选择。