垂索-辅助索系统的建模与固有特性

孙测世，焦德望，赵碧航，谭 超

(重庆交通大学土木工程学院，重庆 400074)

斜拉索是斜拉桥的主要承重结构，具有柔度大、阻尼低等特点，极易发生大幅振动，对桥梁的安全造成重大影响[1-2]。为了抑制斜拉索可能产生的大幅振动，工程上常采用气动措施[3]、安装阻尼器[4-7]或辅助索等措施。但随着斜拉索的长度不断增长，结构非线性和垂度效应的影响逐渐增大，阻尼器因受安装位置的限制达不到理想的减振效果[8]。近年来，辅助索被认为是解决这一难题的有效手段[9]，为此研究人员对拉索-辅助索系统进行了大量的理论研究和实验研究。

早期研究中，为计算简便，将拉索简化为紧绷的弦。CARACOGLIA 等[10-11]建立了由辅助索连接水平弦的模型，基于解析和数值计算方法研究了系统的面内自由振动特性，并将该方法应用于一座既有斜拉桥的减振研究，证明了该方法的有效性。AHMAD 等[12-14]建立了水平弦-辅助索模型，理论分析了模型中各参数对系统面内刚度及阻尼特性的影响。GIACCU 等[15-17]采用基于能量的“等效线性化”方法研究了辅助索连接水平弦系统的非线性自由振动特性，并将模型应用到了既有桥梁的减振研究中。HE 等[18]研究了沿水平弦均匀布置弹性辅助索来抑制弦的振动，研究表明辅助索的刚度和间隙率显著影响系统的模态频率和振型。CHEN 等[19]建立了多个辅助索连接水平弦系统模型，研究了不同参数下弯曲刚度对系统自由振动特性的影响。值得一提的是，以孙利民和周海俊为杰出代表的国内学者在辅助索减振、辅助索加阻尼器复合减振的力学建模、理论分析和试验研究中开展了一系列的系统研究[20-23]，如：SUN 等[20]建立了由弹簧并联阻尼器组成的辅助索连接两根水平弦系统模型，并通过复模态分析得到系统特征方程。ZHOU 等[21]建立了采用负刚度阻尼器连接两根水平弦的模型，在近似确定临界粘性阻尼和负刚度的情况下，给出了附加模态阻尼比的渐近解，研究表明辅助索能显著降低两根水平弦的振动效应。除此以外，具有超弹性和高阻尼的形状记忆合金(SMA)辅助索对弦-辅助索系统的振动特性影响也受到了广泛关注[24-26]。

随着拉索长度不断增大，垂度效应不容忽视，若干最新研究均考虑了垂度影响。2019 年起，SUN 等[27]首先建立了考虑垂度的拉索-辅助索模型，研究表明垂度几乎影响系统的所有振动模式，只有特定模式的频率与垂度无关。其后，CHEN 等[28]提出了一种基于分量模态综合法的索网自由振动和强迫振动分析的通用数值模型，并与SUN 的模型进行了对比分析。AHMAD[29]建立了双悬索-辅助索系统模型，讨论了考虑垂度和忽略垂度情况下不同参数对垂索-辅助索系统一阶频率的影响，研究表明忽略垂度影响会造成非常大的误差。DI等[30-31]进一步考虑了含有预张力的辅助索连接两根小垂度拉索的模型，研究了辅助索预张力对垂索-辅助索系统动力特性影响。

综上所述，辅助索对斜拉索减振有着广阔的应用前景，已受到国内外学者的广泛关注。目前，垂索-辅助索模型多是在有量纲或部分无量纲化前提下进行的推导，或者推导过程并非直接从无量纲运动方程出发，不便更好地把握系统关键参数及其物理意义。另外，对于考虑垂度的拉索-辅助索系统，关键参数对系统固有特性影响的研究尚需进一步丰富。为此，本文推导了由N根垂索和M道辅助索组成的索网系统的无量纲运动方程，建立了垂索-辅助索动力学模型；然后，退化到双索-辅助索系统，并求得其无量纲频率方程和模态方程；最后，研究了系统关键参数对固有特性的影响，以期为后续辅助索减振设计提供理论参考。

1 动力学模型

1.1 垂索-辅助索动力学模型的建立

图1 表示由辅助索(忽略质量)连接小垂度拉索[32]构成的一般垂索-辅助索系统，垂索总数为N，辅助索总道数为M，共计M(N+1)段。每根拉索的单位质量、长度、水平张力、轴向刚度分别为。每根辅助索刚度为，其中j=1, 2, ···,N+1，表示 第j根 拉 索，p=1, 2, ···,M+1，表示第p索段。整个垂索-辅助索系统中的拉索可分成N(M+1)个索段，各索段的长度为，其中j=1, 2,···,N，p=1, 2, ···,M+1。

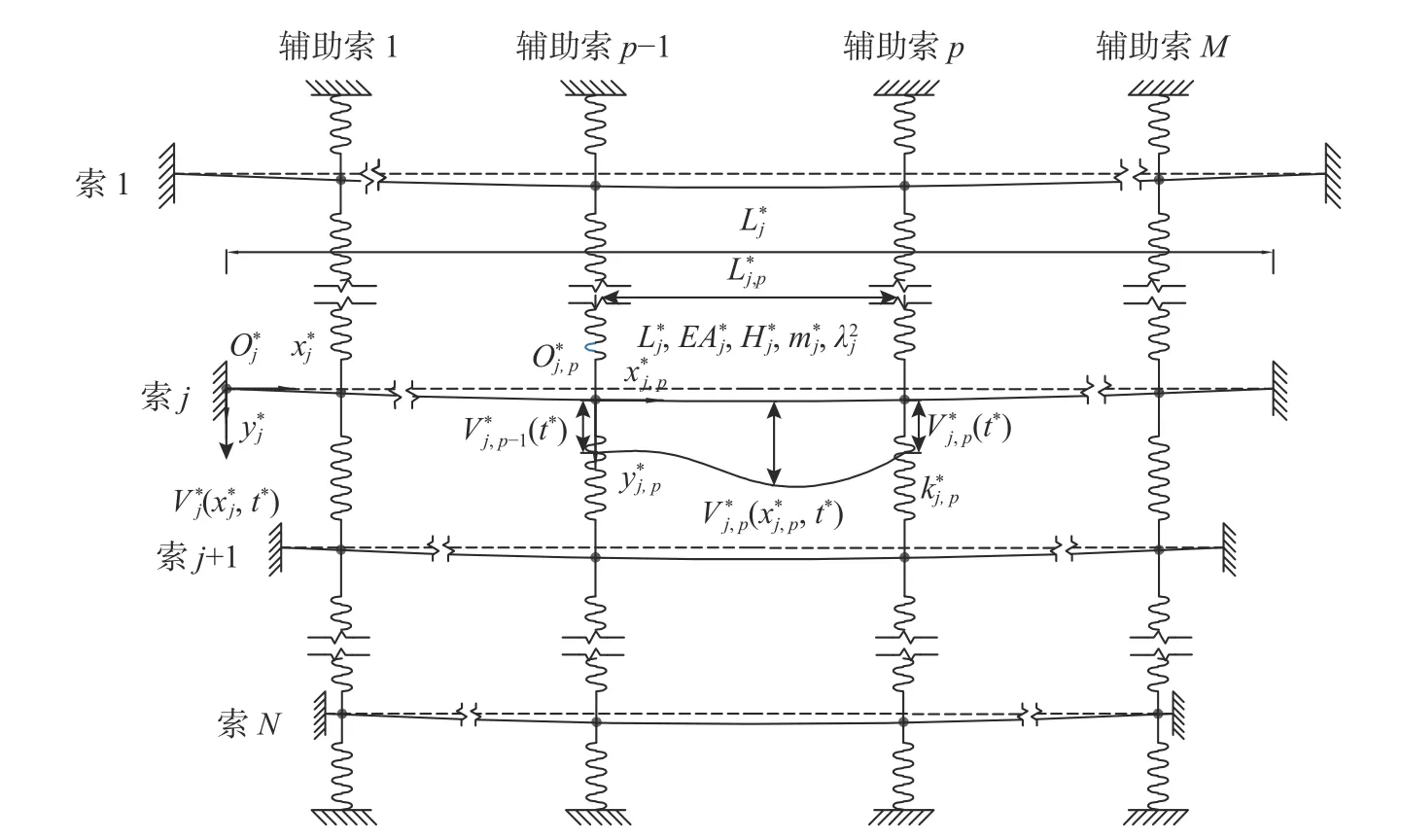
图1 垂索-辅助索系统Fig.1 The sagged-cable-crosstie system

如图1 所示在各拉索j建立局部直角坐标系，xj从拉索左端开始，yj(xj)表示拉索j的初始位移。在自重作用下拉索的初始构型为：

式中，g*为重力加速度。为表示各索段的动态位移，以各索段左端为原点建立了如图1 所示的索段局部直角坐标系。表示第j根索第p段的动态位移，其中j=1, 2, ···,N+1；p=1, 2, ···,M+1。每个索段考虑垂度的运动方程均可采用Irvine 的拉索经典理论方程表示[32]，即：

为使运动方程式(4)更具一般性，引入无量纲量：

式中，L*为使垂索-辅助索系统在统一空间尺度下进行无量纲化而引入的任意长度。当L*=L*j时，即表示其他索的空间无量纲化均按第j根的索长进行。

利用式(5)对式(4)进行无量纲化处理，可得无量纲运动方程：

式中：

显然，式(6)是考虑垂度的无量纲波动方程，其中：参数εj,p反映辅助索的安装位置；为索j的Irvine 参数；1/αj是索j的无量纲波速。αj是对式(4)进行无量纲化处理的过程中产生的参数，本质上是将系统在统一时间尺度下进行无量纲化而引入的综合参数，其中包含了整个垂索-辅助索系统的索力和与质量和之比(对应系统的波速)，又包含了索j的索力与质量比(对应索j的波速)。由于式(6)为彻底无量纲化后动力学方程，具有普适性，物理世界中图1 所示的所有索网结构均由该方程描述。由式(6)还可知，系统运动方程仅依赖于εj,p、和αj三个参数，这是后续开展参数分析的重要基础，而若不进行无量纲化处理很难直接掌握这三个反映系统动力学本质的基础参数。

1.2 垂索-辅助索动力学模型的通解

采用分离变量法将运动方程式(6)中的空间和时间进行分离，令：

将式(7)代入式(6)并求解可得任意索段的模态函数：

式 中：βj=αjω为 索j横 向 振 动 的 无 量 纲 波 数；Bj,p和Dj,p为各索段模态函数的未知常数。

对式(8)两边从0～εj,p积分，并将各段索相加后再回代入式(8)可得：

式中，Qj为垂度产生的附加项，其表达式为：

是一个有量纲波数，而本文中的βj为无量纲波数，是一个反映了索j和整个结构之间关系的综合参数。

1.3 垂索-辅助索动力学模型的定解

为了得到模态频率和模态振型，依次引入拉索的边界条件、位移连续条件和辅助索两端节点处力的平衡条件。

将式(10)代入式(9)可得：

联立整个索网N根拉索的边界条件代入式(11)共可得到2N个方程。

由辅助索kj,p和拉索j的节点处力的平衡条件(假设辅助索拉力为正)可得：

将式(9)和式(11)代入式(12)可得：

联立整个索网N×M个节点处的力平衡条件代入式(13)共可得到N×M个方程。

在辅助索kj,p和拉索j的节点左右需满足位移连续条件，则有：

将式(9)代入式(14)，得：

联立整个索网N×M个节点处的位移连续条件，代入式(15)共可得到N×M个方程。

综上，由式(11)、式(13)和式(15)联立可以得到2N(M+1)个方程，整个索网中各索段模态函数的未知数Bj,p和Dj,p总数也为2N(M+1)个，因此，将方程联立并写成矩阵形式可得：

式中：S= {B1,1,B1,2, ···,B1,p, ···,B1,M+1,D1,1,D1,2, ···,D1,p, ···,D1,M+1, ···,Bj,1,Bj,2, ···,Bj,p, ···,Bj,M+1,Dj,1,Dj,2, ···,Dj,p, ···,Dj,M+1, ···,BN,1,BN,2, ···,BN,p, ···,BN,M+1,DN,1,DN,2, ···,DN,p, ···,DN,M+1}T为一个包含整个索网各索段模态函数的未知数Bj,p和Dj,p的向量；0 为零向量；R为2N(M+1)阶的系数矩阵。显然S不等于0，因此令系数矩阵R对应的行列式等于0，即可求得N根垂索和M道辅助索组成的索网系统的频率方程，进而可以求得各阶频率和模态。

2 双索-辅助索系统退化模型

实际应用时，一根辅助索可能仅连接少量拉索，如近年对苏通大桥开展的辅助索减振实桥研究中便是连接3 根斜拉索[28]。因此，为便于讨论，本文暂考虑最简单的情况，将垂索-辅助索一般模型退化到一根辅助索连接两根拉索的结构，即N=2、M=1。此时，方程中j=1, 2；p=1, 2。另外，令L*=L*1。此时式(16)中的S={B11,B12,D11,D12,B21,B22,D21,D22}T为一个包含8 个未知常数的向量；R为一个8 阶的系数矩阵(见附录)。

系统的频率可以通过令系数矩阵R的行列式等于0 求得，展开行列式进行三角函数简化，并合并同类项，可得系统的频率方程：

其中：

式(17)中第一项为不考虑垂度的项，其余三项为考虑垂度影响的项，当γj=0 时便可以得到忽略垂度影响的频率方程：

式(18)进行一定量纲处理可还原到AHMAD[12]的频率方程；同时，若考虑两所参数相同，则式(18)可进一步化简为：

式(19)经过一定量纲处理亦与ZHOU[22]推导频率方程忽略阻尼影响后的情形一致。

当式(17)中的k2,1取无穷大时方程可退化为：

式(20)亦可通过一定量纲处理还原到SUN 等[27]研究的刚性辅助索的情形。

3 模型验证

3.1 双索单辅助索退化模型验证

为验证方程推导的正确性，参照AHMAD[29]论文中拉索的参数进行计算，并与其计算结果对比。两根拉索参数为：

辅助索放置在拉索的1/4 截面处，其刚度取无穷大，将上述参数代入式(17)，分别求得系统考虑垂度(=2)和忽略垂度(=0)情况下前十阶无量纲频率，再将频率转化为有量纲频率与AHMAD[12,29]论文进行对比；另外，利用上述拉索参数采用有限元软件ANSYS 算得的前十阶频率结果如表1 所示。由表可知：本文求得的频率有量纲化后与AHMAD 的解相同，同时与ANSYS结果也非常接近，说明方程推导的正确性。

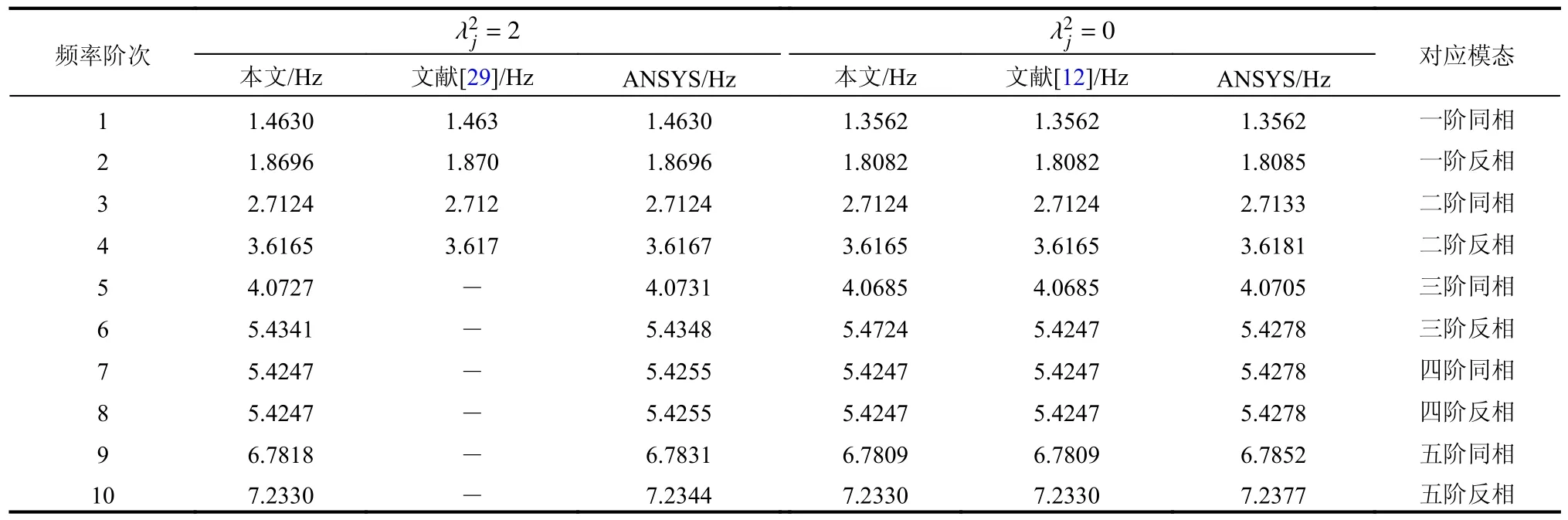
表1 模态频率对比Table 1 Comparison of frequencies

从表1 可以看到，各阶模态振动均对应两个频率，这是由于各阶模态振动均含有两个模态振型，即同相振型和反相振型，较小的频率对应同相振动模态振型，较大的频率对应反相振动模态振型[24]。另外，还可以发现，当=0 时，第三阶反相、第四阶同相、第四阶反相振动频率相同，这与辅助索刚度和位置有关。

3.2 五索双辅助索复杂模型验证

为进一步验证本文推导方程对更复杂索网的正确性，参照AHMAD[33]拉索参数(表2)建立了由2 道辅助索连接5 根拉索的模型。2 道辅助索布置在第一根拉索的L1/3 处，辅助索无量纲刚度取100。求得忽略垂度(λ=0)情况下前10 阶无量纲频率，再将频率转化为有量纲频率与AHMAD[33]论文进行对比；同时，建立ANSYS 模型进行对比，结果如表3 所示。可见，本文所求频率有量纲化后与AHMAD 论文[33]及ANSYS 结果均非常接近。

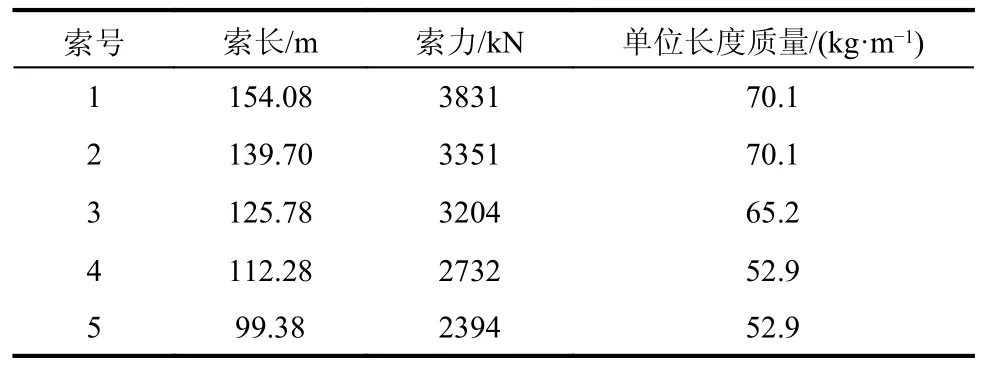
表2 拉索参数[33]Table 2 Cable parameters

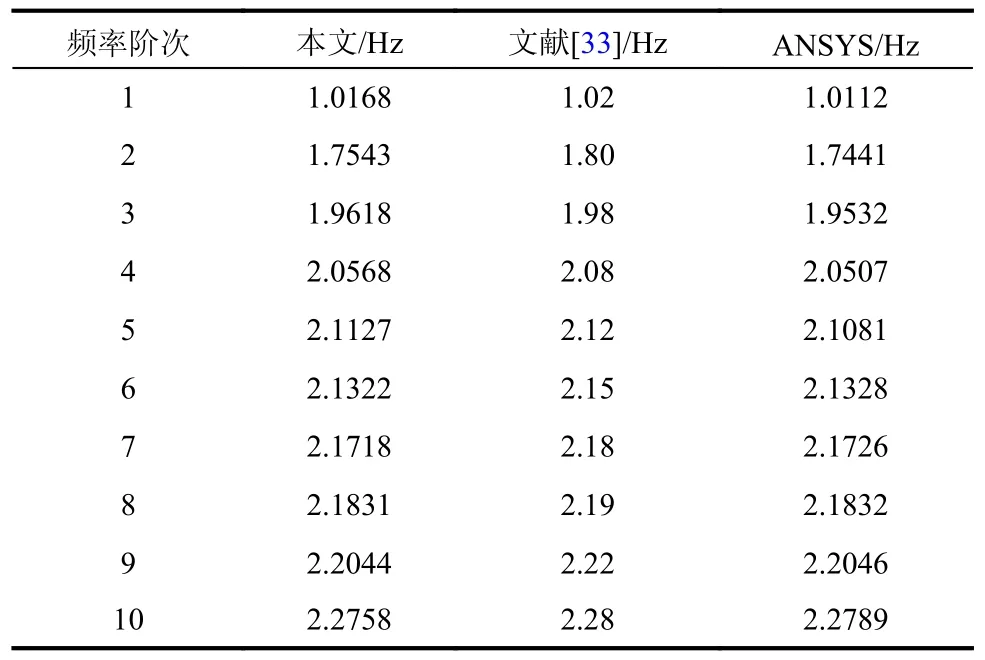
表3 模态频率对比Table 3 Comparison of frequencies

4 参数分析

从式(17)可以看出，垂索-辅助索系统的模态和频率取决于4 个关键参数，即：式(6)所示的εj,p、和αj以及由平衡方程引入的kj,p。当然，拉索间无量纲波速1/αj的差异以波速比参数η 计入，即：

因此，本节以3.1 小节的退化模型为对象，针对Irvine 参数、辅助索刚度k2,1和位置ε2,1、波速比η 四个关键参数开展参数分析，分别讨论它们对系统固有特性的影响。

4.1 Irvine 参数

本小节考虑两根拉索参数相同，其索力、单位长度质量及长度均取3.1 小节中数值，辅助索刚度k2,1=10，辅助索位置ε2,1=0.3。直接改变参数大小，研究对垂索-辅助索系统频率及模态的影响。

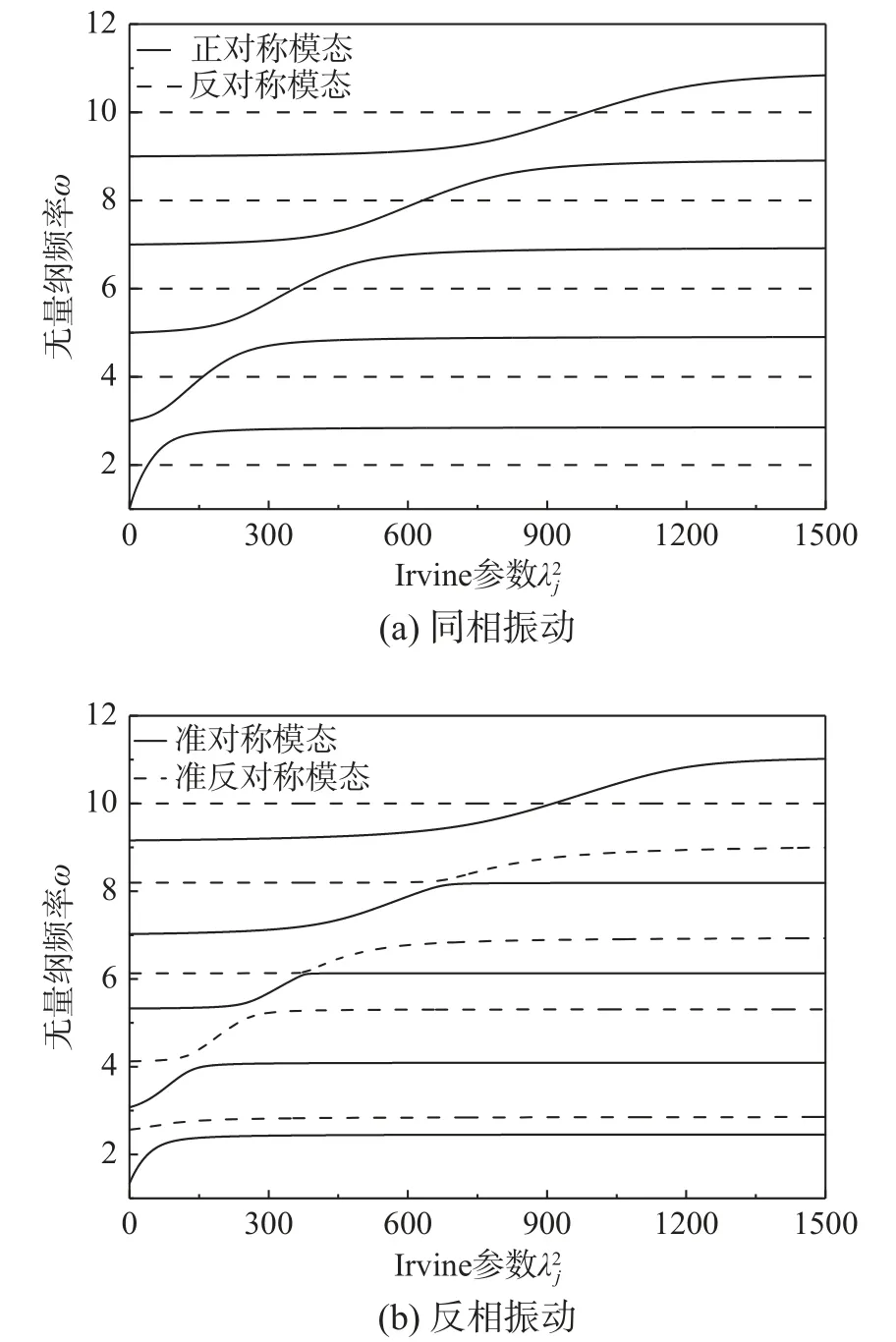
图2 曲线Fig.2 Curvesof

综上，图2(a)由于是同相振动，辅助索不起作用，所以表现出单一悬索的固有特性，ω-曲线出现“穿越”(cross-over)现象，而图2(b)的反相振动中，辅助索起作用，客观上破坏了模态的对称性。这和斜拉索中重力效应下的模态对称性破坏类似，因此ω-曲线表现为“转向”(veering)现象。但若辅助索恰好位于模态节点处，则仍表现为“穿越”现象。

为进一步考察同相振动和反相振动固有特性间的关系，将图2(a)和图2(b)中第一个“穿越”点附近的频率曲线绘于图3(a)。同时，考虑辅助索刚度对一阶反相振动频率的影响，增加k2,1=500(相对刚性)时的一阶反相振动频率曲线。图3(b)为图3(a)中的部分典型模态。由图3(a)可知：<39.48 时一阶反相振动频率大于一阶同相振动，其原因是，反相振动中辅助索发挥了作用，辅助索刚度越大垂索-辅助索系统反相振动频率越大。随着逐渐增加，一阶同相振动频率曲线增长速度最快，辅助索刚度对索网反相振动频率的贡献越来越低，同时，一阶反相振动模态形状逐渐向二阶转变(图3(b))。当=39.48 时，3 条一阶频率曲线与二阶同相振动的频率曲线相交于“穿越”点。从模态图可知：此时对于一阶反相振动，辅助索两端正好处于索的不动点处(模态的节点处)，故失去了其作用。因此，同相和反相振动频率相等，不同辅助索刚度下的固有频率也相等，从而出现4 条曲线交汇于同一点的现象。当>39.48 时，3 条一阶振动频率曲线均越过二阶同相振动频率曲线。此后，一阶同相振动频率均大于反相振动频率。辅助索对一阶反相振动频率和模态重新起作用，因此k2,1=500 的频率曲线一直处于k2,1=10 之上。值得注意的是，一阶同相振动模态呈现3 个半波，而一阶反相振动为2 个半波。

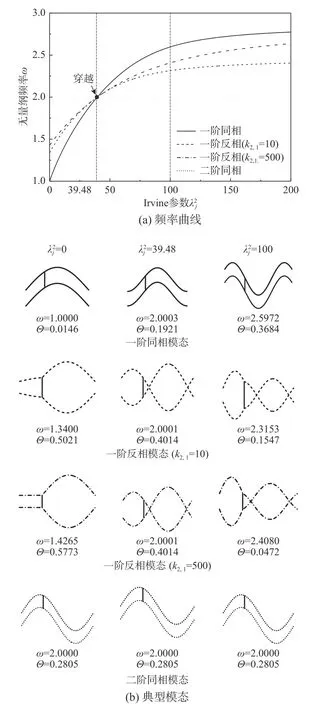
图3 第一个“穿越”点附近频率曲线和典型模态图Fig.3 Frequency curves and typical modes near the first cross-over point

为进一步分析系统模态的局部振动模态特性，利用ZHOU 等[23]提出的衡量模态局部化指标方法，结合GATTULLI 等[34]在研究斜拉桥索-梁-塔耦合振动时，提出的衡量拉索局部振动的指标，给出以下反映索网系统模态局部化的指标计算公式：

式中：

为第j根索第p段的模态势能与整个索网系统模态势能之比。显然，Θ 取值范围为[0,1]，Θ 越大，模态局部化程度越高。从图3(b)可以看出：随着的增大，一阶同相模态局部化程度增大；一阶反相模态的局部化程度则随增大而降低；二阶同相模态不受影响，Θ 保持不变。

4.2 辅助索位置ε2,1 及刚度k2,1

由理论推导可以看出，辅助索的位置及刚度是影响其作用效果的关键因素，为此通过改变式(17)中的参数k2,1和ε2,1来研究辅助索刚度及位置对系统频率及模态的影响。两根拉索的索力、质量及长度均取3.1 节中数值，另外取=2。

图4 是系统前四阶频率随辅助索位置及刚度变化而改变的曲面图。由图可知，各阶同相振动频率不受k2,1及ε2,1变化的影响，主要原因在于，同步振动时两索间无相对位移，辅助索无作用。反相振动时，两索振动时存在相对位移，且不同位置处大小不同，故辅助索的影响不尽相同。当辅助索位置ε2,1=z/(n+1)时(n为阶次，z为小于n的正整数)，即辅助索安装于两索反相振幅最大处时对系统反相频率的影响最大。当然，即使辅助索设置在这些位置，随着刚度的增大，各阶反相振动频率并不会无限增大，而是接近于高一阶次的同相振动频率，即辅助索的安装位置和刚度最多能使系统无量纲频率增大1。

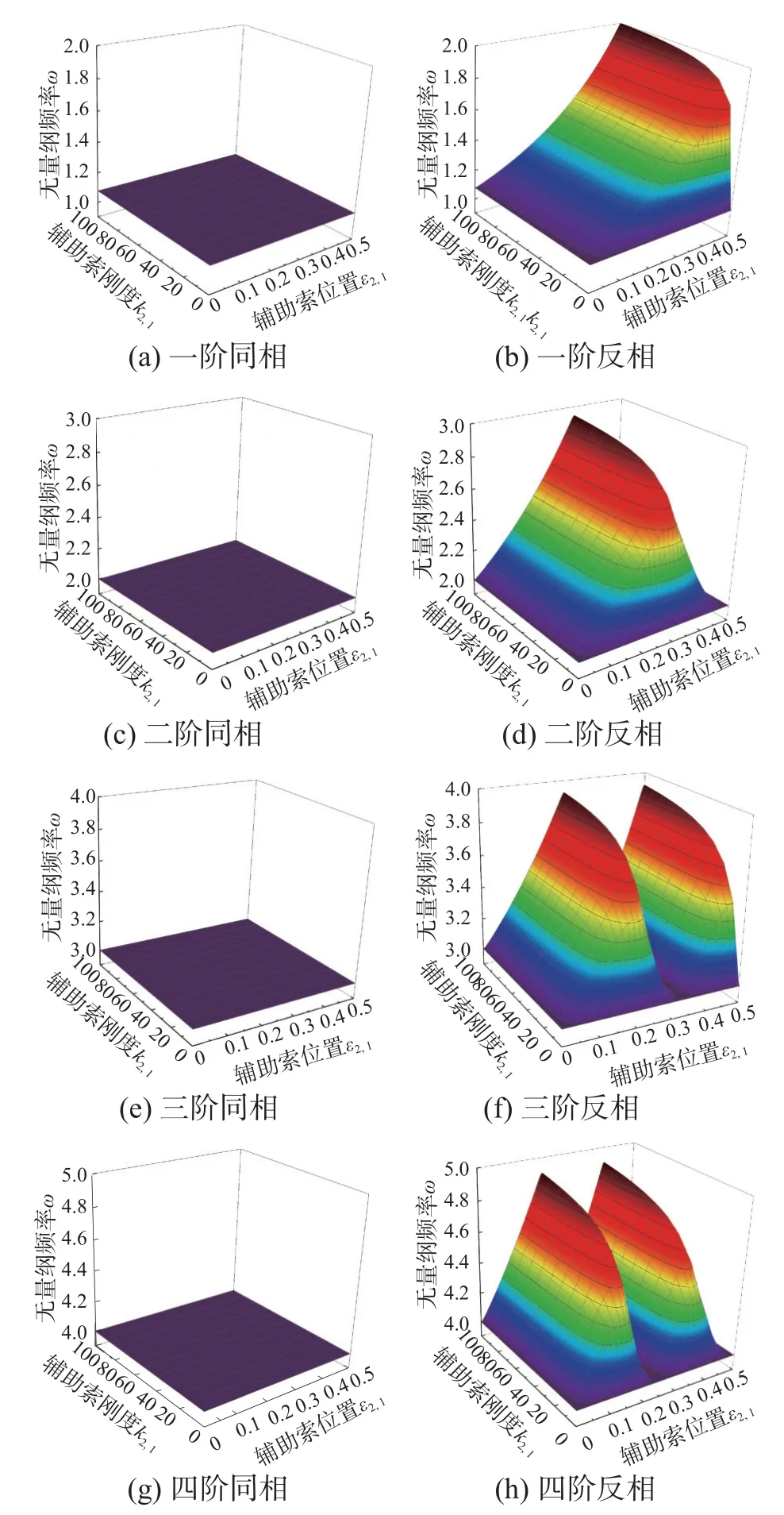
图4 ω 的三维曲面图Fig.4 The 3-D surfaces of ω

另外，对于反相模态，系统可视为一个以辅助索中点处为对称轴的对称结构，故取其中一半结构则正好可退化至周海俊等[35]所研究的拉索-接地辅助索结构。因此，图4 中各阶反相模态频率随k2,1及ε2,1变化的规律与文献[35]完全一致。

图5 是图4 中频率对应的典型模态，对比图5(a)和图5(b)中的第三阶反相振动模态可以发现，若采用大刚度辅助索，其将抑制索振动位移，从而提高系统的刚度；另外，当ε2,1=0.25时，对于第四阶反相振动模态，辅助索两端点间未产生相对位移，辅助索无作用，因此其频率与四阶同相振动的相同，Θ 值亦相同，仅是方向不同而已。值得注意的是，由于刚度的增大各阶反相振动频率并不会无限增大，而是接近于高一阶次的同相振动频率，当=0 时，若k2,1取无穷大，三阶反相振动频率也无限接近于四阶同相振动频率，从而导致表1 中6 阶、7 阶、8 阶三个频率均为5.4247 Hz。

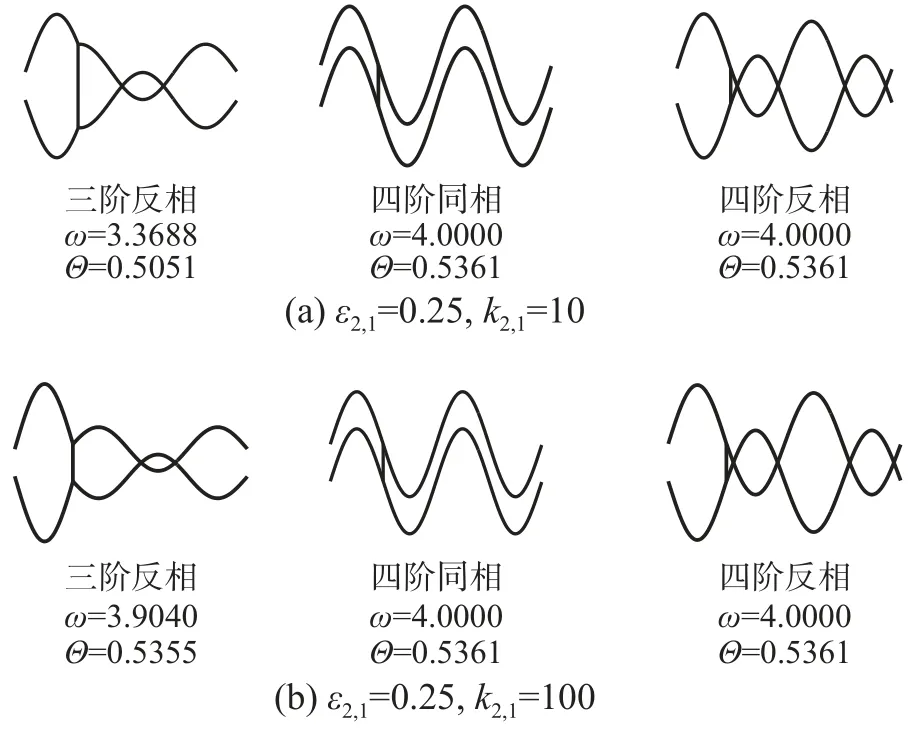
图5 典型模态Fig.5 Typical modes

4.3 波速比η

波速的差异使拉索间产生相对位移，而辅助索的作用将改变垂索-辅助索系统的频率及模态。为此，通过改变η 的大小来研究拉索间参数差异对系统频率和模态的影响。计算时索1 的索力、质量及长度均取3.1 节中数值，索2 的索力及长度与索1 相同，但变化索2 质量，同时为仅研究η 单一参数的影响，保证两根拉索=2 不变。辅助索刚度和位置参数分别取为：k2,1=10，ε2,1=0.3。

计算得到的系统各阶频率ω随η 的变化曲线及典型模态见图6。由图可知，随着η 减小，即两索参数差异变大，各阶频率逐渐增大并出现了跳阶，阶次越高的频率曲线受到η 变化的影响越大，二阶及以上频率随着η 的减小甚至出现了连续跳阶现象，且阶次越高连续跳跃的次数也越多。结合图6(b)模态图也可以看出，随着η 减小，两索间模态位移差异逐步增大，安装辅助索后系统整体刚度和频率增大越显著。

图6 ω-η 曲线图及典型模态图Fig.6 Curves of ω-η and typical modes

从Θ 值来看，二阶同相和三阶反相模态的局部化程度随η 减小而不断增加。从方程上看，η 减小本质上可以认为是索2 质量的减小，在不变的情况下相当于拉索2 垂度降低，等效轴向刚度提高[36-38]，因此系统的整体刚度和各阶固有频率变大，且对高阶频率的影响更明显。其力学原理与禹见达等[36-38]的复合阻尼索设计一致，本质上均是利用副索的支撑作用减小主索垂度，使主索在几何上近乎为一条直线，从而在第一时间承受可能来自端部或横向的载荷，客观上达到提高系统刚度和频率的效果。斜拉桥中相邻拉索的波速往往存在差异，因此，安装辅助索后系统刚度和频率将增大，且对高阶频率的影响大于低阶。

5 结论

本文推导了包含N根垂索和M道辅助索的索网动力学模型，给出了求解频率方程及模态函数的通用表达式，并进行了验证。基于双索-辅助索退化模型进行参数分析，研究了索网系统的固有特性，得到如下主要结论：

(1) 由于本文对垂索-辅助索系统运动方程进行了彻底的无量纲化，故方程更具普适性，且关键参数及其物理意义更明晰。系统运动方程仅依赖于辅助索位置εj,p、Irvine 参数和αj，以及由平衡方程引入的辅助索刚度kj,p四个关键参数。

(2) 当两索参数相同时，系统的同相振动频率曲线以及辅助索恰好位于模态节点处时的反相振动频率曲线随Irvine 参数的增加表现为“穿越”现象，而其它反相振动频率则表现为“转向”现象。特定的Irvine 参数下，任意辅助索刚度对应的系统一阶反相振动频率均等于一阶同相频率，因此出现各频率曲线在第一个“穿越”点交汇的现象。

(3) 当两索参数相同时，辅助索仅影响反相振动频率，且其安装位置和刚度最多能使系统各阶反相频率增大1，因此，仅依赖辅助索刚度和位置来提高系统频率的方式效果有限。

(4) 系统同相和反相频率均随两索波速差异增大而发生往高阶的“跳阶”现象(频率增大)，且频率阶次越高“跳阶”次数越多。实际斜拉桥的拉索波速往往不同，因此安装辅助索后的垂索-辅助索系统高阶频率可能有明显增大，故合理调节两索的参数可在一定程度上突破仅增大辅助索刚度这一手段的限制，进一步提高系统刚度和频率。