配箍率对高强钢筋RPC梁抗剪性能影响研究

金凌志, 梅臣

(1.广西岩土力学与工程重点实验室，广西 桂林 541004；2.桂林理工大学 土木与建筑工程学院，广西 桂林 541004)



配箍率对高强钢筋RPC梁抗剪性能影响研究

金凌志1,2, 梅臣1,2

(1.广西岩土力学与工程重点实验室，广西 桂林 541004；2.桂林理工大学 土木与建筑工程学院，广西 桂林 541004)

摘要:为了研究HRB500级高强钢筋活性粉末混凝土简支梁的抗剪性能，通过改变箍筋配筋率，对4根在集中荷载下的RPC简支梁进行受剪破坏试验，比对分析不同配箍率对试验梁的斜裂缝发展、受剪承载力及最大斜裂缝宽度的影响。试验结果表明：高强箍筋和活性粉末混凝土具有良好的协同工作性能，抗剪延性得到改善；高强钢筋活性粉末混凝土梁的临界斜裂缝一般由腹剪型斜裂缝发展而成；配箍率大小对试验梁的斜向开裂荷载并无明显影响，但是配箍率越高，斜裂缝宽度越小，抗剪承载力越高；桁架-拱理论模型公式比较适用于高强钢筋RPC有腹筋梁抗剪承载力的计算。

关键词：高强钢筋；活性粉末混凝土；配箍率；斜裂缝宽度；受剪承载力

活性粉末混凝土(Reactive Powder Concrete，以下简称RPC)是一种新型水泥基复合材料,具有高强度、高耐久性及高韧性等优良性能[1]，应用前景广阔[2]。由于提高了组分细度、反应活性及掺加了钢纤维，相比普通混凝土梁，活性粉末混凝土梁在抗剪性能上有突出的优势，对其抗剪性能的研究不容忽视。近年来，国内外对活性粉末混凝土的制备、基本力学特性等进行了深入研究[3-5]。陆小吕[6]用ANSYS建立有限元模型，验证所提出的RPC梁极限弯矩计算式。Xia等[7-8]根据RPC梁的抗剪试验结果，提出相适应的塑性剪切理论和黏结滑移理论。武玉赞[9]基于修正压力场理论，充分考虑受拉区钢纤维对混凝土抗拉性能的提高，分析得到钢纤维混凝土梁在弯剪作用下极限抗剪承载力的简化截面分析方法。张浦[10]基于软化桁架模型，系统分析混凝土强度、剪跨比、配箍率等因素对RPC梁抗剪承载力的影响，并初步提出RPC梁抗剪承载力计算的建议公式。金凌志等[11-12]对6根RPC简支梁进行抗剪试验研究，分析配箍率等参数对剪切延性、抗剪承载力以及斜裂缝宽度的影响，表明剪切延性系数和抗剪承载力均随配箍率的提高而提高，并提出RPC梁最大斜裂缝宽度与平均斜裂缝宽度的关系公式。但是国内对高强钢筋活性粉末混凝土梁抗剪性能的研究尚少，参考文献[6-10]主要研究普通钢筋RPC梁的抗剪性能。本文在活性粉末混凝土梁中配置HRB500级纵筋和HRB400级箍筋，在文献[10-11]研究成果的基础上，运用摩尔圆原理，分析试验梁斜裂缝开裂模式均为腹剪型斜裂缝的原因，揭示不同配箍率对试验梁的破坏形态、受剪承载力及斜裂缝宽度等的影响机理。

1试验概况

1.1试件设计

试验将配箍率作为重要参数，分析研究高强钢筋RPC梁的抗剪承载力。4根配有HRB500级钢筋的RPC简支梁，剪跨比λ=2.25，受拉纵筋直径25 mm，HRB400级箍筋，截面尺寸b×h=150 mm×250 mm , 梁长2 200 mm，跨度1 800 mm，试验梁参数及RPC力学性能见表1～2。

1.2原材料

RPC原材料配合比见表3，包括广西兴安海螺牌42.5普通硅酸盐水泥；石英砂：粒径范围0.4～0.6 mm，颗粒呈球形；微硅粉：比表面积20 000 m2/kg，平均粒度范围为0.1～0.2 um，硅灰中SiO2的含量94.7%以上；石英粉：粒径为40 μm，SiO2含量为99.24%；硅微粉：粒径2 μm以下，平均粒径0.31 μm左右；钢纤维：选用镀铜光面平直钢纤维，直径0.22 mm，长度为12～15 mm，抗拉强度>1 200 MPa；小组分；FND浓缩型高效减水剂和水。

表1　试验梁参数

表2　RPC力学性能

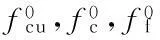
表3　RPC配合比

注：除钢纤维为体积比外，其他均为质量比。

1.3测点布置和加载方案

通过分配梁采用四分点集中单调静力加载方式对试验进行加载，且严格按照参考文献[13]执行。应变片数据通过DH3816静态应变测试系统采集，荷载等级由传感器控制。试验方案见图1。

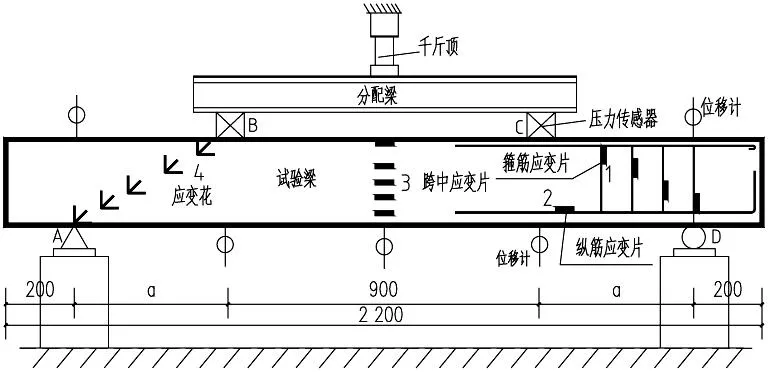
图1　试验方案图Fig.1 Testing scheme figure

2试验现象及破坏形态描述

分析试验现象，JZL-1,2和3的破坏形态都为剪压破坏,只有JZL-4为弯曲破坏。由于活性粉末混凝土的诸多优越性，无腹筋梁在破坏时的延性得到很好改善，有腹筋梁的斜裂缝数量较多，分布更为均匀，说明高强箍筋和活性粉末混凝土具有良好的协同工作性能，抗剪性能优异，箍筋能够很好地约束混凝土的侧向变形和斜裂缝的开展。试验梁的破坏照片见图2～3。

图2　JZL-1，2和3剪压破坏照片Fig.2 Shear compression failure pictures of JZL-1，2 and 3

图3　JZL-4受弯破坏照片Fig.3 Bending failure picture of JZL-4

1)剪压破坏：JZL-1，JZL-2和JZL-3均发生剪压破坏。在荷载作用下，试验梁首先在跨中出现垂直水平方向的弯曲裂缝，接着在剪跨区腹部中和轴附近出现斜裂缝。随着荷载增大，剪跨区出现数条近似平行的斜裂缝，裂缝细而密,宽度增长缓慢。荷载进一步增加，剪跨区出现一条主斜裂缝，不断向加载点和支座处延伸，以宽度变化为主，新裂缝出现缓慢。伴随“噼里啪啦”的声音，大量钢纤维被拔出。伴随“蹦”的一声，穿过斜裂缝的箍筋被拉断，斜裂缝迅速开展形成临界斜裂缝，同时剪压区混凝土被微压碎，加载值开始下落，试验梁宣告破坏。

2)弯曲破坏：JZL-4的箍筋间距比较小，但并未超筋，试验梁没有发生斜压破坏。可能是由于梁的抗剪能力大于其抗弯能力而发生弯曲破坏，其破坏荷载值与JZL-3接近。加载初期，梁跨中底部首先出现微小垂直裂缝，裂缝长度不断沿截面高度缓慢向上延伸，裂缝数量随着荷载的增加增长较快。在加载过程中，第1条斜裂缝出现在剪跨区梁的纵筋合力点处，而跨中弯曲裂缝则以长度发展为主。加载到一定程度，梁跨中处的裂缝宽度发展很快，并伴有“吱吱”的钢纤维拔出声音，挠度增长较大，剪跨区的斜裂缝集中在梁腹部，较为细短且发展缓慢。最后由于纵筋屈服，部分箍筋屈服，且加载点附近的混凝土被微压碎，试验梁丧失承载力，导致最终破坏。

3试验结果及分析

3.1斜裂缝类型

从试验梁的裂缝形态来看，受剪斜裂缝存在2种开裂模式：腹剪斜裂缝和弯剪斜裂缝。弯剪斜裂缝是由剪跨区底部的垂直裂缝发展形成的：加载到一定程度，受弯裂缝沿截面高度向上发展的方向开始发生倾斜，往加载点发展。腹剪斜裂缝通常发生在剪跨区腹部中和轴附近，随着荷载等级的增加，向上下两端发展，而且呈中间大两端小的态势，上下倾角均减小，倾斜角度约在30°～60°之间。

从试验梁的裂缝发展情况来看，4根试验梁均在剪跨区腹部靠近中和轴的位置出现首条斜裂缝，即产生腹剪型斜裂缝，说明高强钢筋RPC梁一般先出现腹剪型斜裂缝。如图4(a)所示，试验梁受力后，最大剪应力产生于中和轴附近，这个区域是受压应力影响最小的区域。在支座和加载点处的集中力使一定范围内的混凝土受到竖向不均匀压应力σy，加载点区域的混凝土单元体处于双向受压状态。分别在剪跨区中部和加载点附近沿高度取3个微元体，根据Mohr应力圆原理，从图4(b)中可以明显看出σA>σB>σC=σD>σE>σF，故在受压区及加载点处，由于压应力或双向受压状态的存在，均有利于降低一定区域内，混凝土单元所受到的主拉应力，从而起到延缓混凝土开裂的效果。相关试验研究表明[14]：在一定区域内，受拉纵筋对其周围的混凝土有较好的约束作用，并能够调节混凝土的内力重分布和抑制混凝土内部原本微裂缝的扩展。剪跨区弯曲裂缝出现后，RPC梁较高配筋率的纵向钢筋对受拉区裂缝的延伸和开展具有一定的约束作用，从而延缓了弯剪斜裂缝的形成，而随着截面高度增加，纵向钢筋的销栓作用减弱，剪跨区腹部的混凝土主拉应力增长较快，导致腹剪斜裂缝的形成和发展。综上所述，高强钢筋RPC梁的剪跨区梁中和轴附近更容易成为首先开裂的区域，临界斜裂缝一般由腹剪型斜裂缝发展而成。

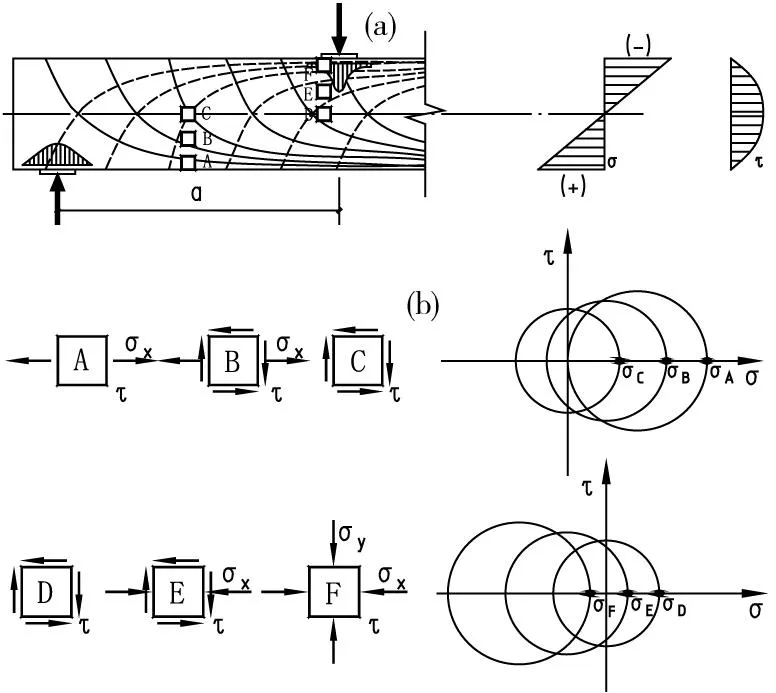
(a)试件主应力轨迹线及应力分布；(b)单元体应力及摩尔应力圆图4　剪跨区的应力分布及摩尔应力圆Fig.4 Stress distribution of shear span and Mohr stress circle

3.2开裂荷载与极限荷载

3.2.1开裂荷载

试验梁的剪跨区同时存在腹剪型和弯剪型2种斜裂缝形式。腹剪斜裂缝以剪跨区中和轴附近出现斜裂缝时的荷载作为斜向开裂荷载，而对于弯剪斜裂缝，则以垂直裂缝产生明显倾角作为出现弯剪斜裂缝的起点，4根试验梁均首先出现腹剪斜裂缝，且主斜裂缝均由腹剪斜裂缝上下延伸发展而来，故斜向开裂荷载即为腹剪裂缝出现时对应的荷载值。

从图5可以看出：1)由于箍筋直径较小，抑制混凝土内部微裂缝扩展的作用很小，且斜裂缝出现前，剪应力大部分由混凝土承担，配箍率的大小对高强钢筋RPC梁斜向开裂荷载的影响甚微；2)试验梁JZL-1，JZL-2和JZL-3配箍率分别为0%，0.168%和0.252%，抗剪承载力分别提高了17.7%和2.77%，配箍率提高，单位面积上的箍筋密度增大，箍筋对混凝土侧向变形的约束增强，从而提高了梁的受剪承载力；3)配箍率增大到一定程度后，试验梁的斜截面受剪承载力可能逐渐接近其正截面受弯承载力，构件破坏模式则可能由剪压破坏向受弯破坏转变，虽然梁的延性提高，但抗剪承载力由于纵筋屈服而略有下降。

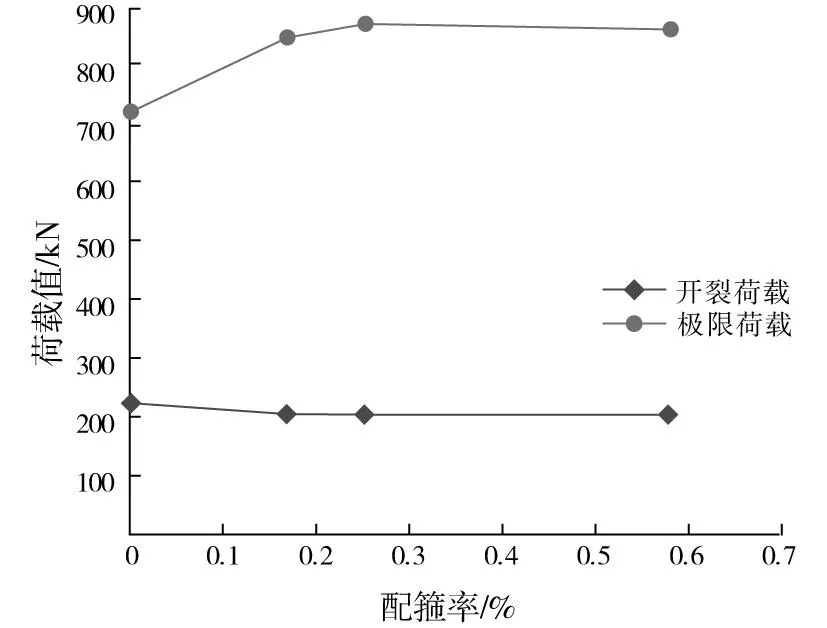
图5　开裂荷载和极限荷载与配箍率的关系曲线Fig.5 Curves of relationship between stirrup ratio and cracking load and ultimate load

3.2.2极限荷载

桁架-拱理论认为，桁架作用和拱作用同时存在于有腹筋梁的受剪过程中，受压混凝土既可视为受压上弦杆又可作为拱腹，底部纵筋则被视为受拉下弦杆，将箍筋和箍筋间混凝土比拟成桁架的竖杆和斜腹杆。文献[15]以桁架-拱模型为基础，对受剪机理开展了进一步的研究，将剪跨区划分成5类区域，并综合考虑箍筋和混凝土抗压强度的影响，以支座与加载点连线区域上的混凝土达到抗压强度作为试验梁的受剪破坏准则，简化分析得出斜截面抗剪承载力计算式(1)～(2)，其中m=1+(ρsvfyvλ2)/fc。

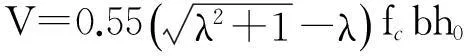
(1)

(2)

目前，对于钢筋混凝土梁抗剪承载力的计算理论和方法较多，且各国规范计算公式所考虑的抗剪因素略有不同。本文选取桁架-拱理论模型和美国规范ACI318-08的计算结果与试验实测值进行对比分析，计算结果见表4。

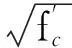
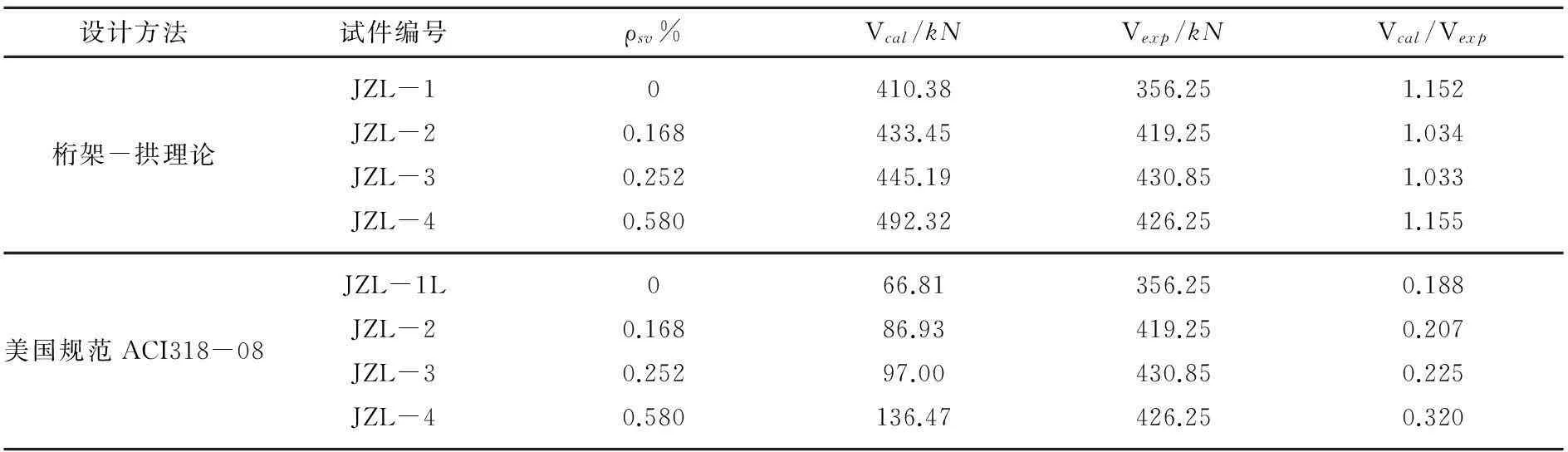
表4　RPC梁抗剪强度的计算值与试验值对比

表5　试件斜裂缝宽度

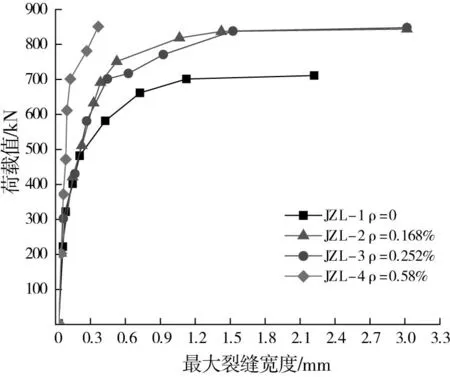
图6　箍筋率对斜裂缝的影响曲线Fig.6 Influence curves of stirrup ratio to inclined cracks

3.3配箍率对斜裂缝宽度的影响

从表5和图6可以看出：1)斜裂缝出现以后，曲线斜率变化以500 kN左右为分界点，在分界点前，有腹筋梁与无腹筋梁的曲线斜率大致相同，表明在斜裂缝出现后的一段范围内，混凝土逐步退出工作，而开裂释放的应力主要由RPC中的钢纤维承担，钢纤维跨越斜裂缝，通过“桥架”作用限制斜裂缝的发展[16]；在分界点之后，曲线斜率差异明显，无腹筋梁的曲线斜率逐渐减小，说明HRB400级高强箍筋对斜裂缝的抑制作用显著增强；2)从斜裂缝出现到破坏，无腹筋梁的主斜裂缝发展速度明显高于有腹筋梁。在相同荷载等级下，试验梁的最大斜裂缝宽度随配箍率的增加而降低，有腹筋梁JZL-2和JZL-3的最大斜裂缝宽度分别比无腹筋梁JZL-1降低48.6%和42.8%；3)试验梁JZL-2与JZL-3的配箍率分别为0.17%和0.25%，箍筋率对斜裂缝的影响曲线发展趋势大致相同，配箍率只在发展过程中的某一阶段对裂缝宽度的发展速度有影响，而对其初始与最大斜裂缝宽影响不大；4)有腹筋梁JZL-4的最大斜裂缝宽度增长速度明显低于发生剪压破坏的梁，破坏时纯弯段受弯裂缝宽度超过限值，说明箍筋配置过多时，以纯弯段弯曲裂缝发展为主，有明显的受弯破坏趋势。5)高强箍筋对初始斜裂缝宽度有明显的约束作用，有腹筋梁初始斜裂缝宽度比无腹筋梁降低50%，而有腹筋梁的初始斜裂缝宽度基本相同，并不随配箍率的提高而降低。

4结论

1)由于活性粉末混凝土的诸多优越性，试验梁的延性得到很好改善，有腹筋梁比无腹筋梁的斜裂缝数量更多，间距更密，分布更均匀，且高强钢筋RPC梁的临界斜裂缝一般由腹剪型斜裂缝发展而成；

2)高强钢筋RPC梁的混凝土强度等级和纵筋率都比较高，梁截面尺寸比较小，刘立新于桁架-拱理论模型推导的公式，比较适用于高强钢筋RPC有腹筋梁抗剪承载力的计算；

3)增大配箍率可以提高试验梁的极限抗剪承载力，但对试验梁斜裂缝的初始宽度无显著影响，斜裂缝宽度大约0.3 mm时，箍筋的作用才显著增强。在相同荷载作用下，斜裂缝宽度随配箍率的提高而降低。箍筋能够有效限制初始斜裂缝的宽度，延缓腹剪斜裂缝向梁的支座和加载点连线两端发展。

参考文献:

[1] Dugat J，Roux N， Bernier G.. Mechanical properties of reactive powder concretes[J].Materials and Structures，1996，29(5):233-240.

[2] 杨剑，汪金胜，彭鑫. RPC在无砟轨道中的应用研究与展望[J].铁道科学与工程学报，2015，12(1)：53-58.

YANG Jian，WANG Jinsheng，PENG Xin. Application and outlook of RPC in ballastless track[J]. Journal of Railway Science and Engineering，2015，12(1)：53-58.

[3] 闫光杰，阎贵平，安明喆.200 MPa级活性粉末混凝土试验研究[J].铁道学报,2004,26(2)：116-119.

YAN Guangjie，YAN Guiping，AN Mingzhe. Experimental study on 200 MPa reactive powder concrete[J]. Journal of the China Railway Society，2004，26(2)：116-119.

[4] 单波，杨吴生，黄政宇.钢纤维对RPC抗压强度增强作用的研究[J].湘潭大学自然科学学报,2002,24(1)：109-112.

SHAN Bo，YANG Wusheng，HUANG Zhengyu. Effect of steel fiber on improving compressive strength of RPC[J]. Natural Science Journal of Xiangtan University， 2002，24(1)：109-112.

[5] 原海燕.配筋活性粉末混凝土受拉性能试验研究及理论分析[D].北京：北京交通大学,2009.

YUAN Haiyan. Theoretical analysis and experimental research on tensile performance of reinforced reactive powder concrete[D].Beijing：Beijing Jiaotong University，2009.

[6] 陆小吕.活性粉末混凝土矩形截面配筋梁正截面受弯的计算方法研究[D].北京：北京交通大学,2011.

LU Xiaolv. Study of the calculating method of crack resistance and flexural capacity for rectangular reinforced RPC beam[D].Beijing：Beijing Jiaotong University，2011.[7] Xia Jun, Kevin M.Shear failure analysis on ultra-high performance concrete beams reinforced with high strength steel [J].Engineering Structures,2011,33:3597-3609.

[8] Reineck K H.Ultimate shear force of structural concrete member without transverse reinforcement derived from a mechanical model [J]. ACI Struct J,1991,88(5):592-602.

[9] 武玉赞.基于修正压力场理论的钢纤维混凝土梁抗剪研究[D].大连：大连理工大学，2008.

WU Yuzan. Study on shear capacity of steel fiber reinforced concrete beams based on the modified compression field theory[D].Dalian：Dalian University of Technology，2008.

[10] 张浦.基于软化桁架理论的RPC梁斜截面抗剪承载力研究[D].北京：北京交通大学，2011.

ZHANG Pu. Study on oblique section shear-bearing capacity of RPC beam based on softened truss theory[D].Beijing：Beijing Jiaotong University，2011.

[11] 金凌志，祁凯能，曹霞.高强钢筋活性粉末混凝土简支梁受剪性能试验研究[J].武汉理工大学学报,2013，35(8)：108-113.

JIN Lingzhi，QI Kaineng，CAO Xia. Experimental study on shear behavior of high strength reinforced reactive powder concrete beam[J].Journal of Wuhan University of Technology，2013，35(8)：108-113.

[12] 金凌志，何培，祁凯能，孙凌云.高强钢筋活性粉末混凝土简支梁斜裂缝宽度试验研究[J].武汉大学学报(工学版), 2014,47(5)：665-670.

JIN Lingzhi，HE Pei，QI Kaineng，SUN Lingyun. Experimental study of diagonal crack width of high strength reinforced reactive powder concrete simply-supported beam[J]. Engineering Journal of Wuhan University，2014，47(5)：665-670.

[13] GB/T50152—2012, 混凝土结构试验方法标准[S].

GB/T50152—2012，Standard for test method of concrete structure[S].

[14] 姜鹏.钢筋钢纤维高强混凝土梁斜截面受力性能试验研究[D].郑州：郑州大学，2005.

JIANG Peng. Experimental study on oblique section mechanical behavior of steel fiber reinforced high-stength concrete beam[D].Zhengzhou：Zhengzhou University，2005.

[15] 刘立新.钢筋混凝土深梁、短梁和浅梁受剪承载力的统一计算方法[J].建筑结构学报, 1992,16(4)：13-21.

LIU Lixin. An unified calculation method for shear capacity of R.C.deep beams, short beams and shallow beams[J]. Journal of Building Structures，1992，16(4)：13-21.

[16] 张宏战.钢纤维高强混凝土构件受剪性能试验研究[D].大连：大连理工大学，2005.

ZHANG Hongzhan. Experimental study on shear resistance properties of steel fiber reinforced high-strength concrete members[D].Dalian：Dalian University of Technology，2005.

Study on the influence of stirrup ratio to shear performance of RPC beams with high strength reinforcementJIN Lingzhi1,2, MEI Chen1,2

(1.Guangxi Key Laboratory of Geomechanics and Geotechnical Engineering, Guilin 541004,China;2.College of Civil Engineering and Architecture, Guilin University of Technology, Guilin 541004, China )

Abstract：In order to study the shear performance of reactive powder concrete simply supported beams with HRB500 level high strength reinforcement, four RPC beams’ shear failure experiment was carried out under concentrated load by changing the stirrup ratio. The influence of different stirrup ratio on diagonal cracks development, bearing capacity of the testesd beams, and the maximum diagonal crack width shear are compared and analyzed. Test results show that high-strength stirrups and reactive powder concrete can work coordinately, and the shear ductility is improved. Generally, critical diagonal cracks of reactive powder concrete beams with high strength reinforcement are formed by the development of abdominal shear diagonal cracks. Stirrup ratio of the tested beams had no obvious effect on the diagonal cracking load. With the increase of stirrup ratio, the diagonal crack width becomes smaller, and the shear bearing capacity becomes higher. Truss-arch theory model formula is suitable for the shear bearing capacity calculation of high strength reinforced RPC beams with stirrups.

Key words：high strength reinforcement; reactive powder concrete; stirrup ratio; diagonal crack width; shear bearing capacity

中图分类号：TU375.1；TU371.1

文献标志码：A

文章编号：1672-7029(2016)04-0711-06

通讯作者：金凌志(1959-)，女，湖南双峰人，教授，从事新型混凝土材料结构研究；E-mail:jlz-5904@163.com

基金项目：国家自然科学基金资助项目(51368013)；广西重点实验项目资助(2015-A-02)

收稿日期：2015-07-10