不同工况下沥青混合料黏弹性参数研究

彭东黎，张家生，龙尧

( 1. 湖南交通职业技术学院 工程经济学院， 湖南 长沙 410132;2. 中南大学 土木工程学院，湖南 长沙 410075)



不同工况下沥青混合料黏弹性参数研究

彭东黎1，张家生2，龙尧2

( 1. 湖南交通职业技术学院 工程经济学院， 湖南 长沙 410132;2. 中南大学 土木工程学院，湖南 长沙 410075)

摘要:通过AC-20C沥青混合料不同工况下室内车辙试验，采用循环应力下的沥青混合料本构模型，分析温度、荷载和作用时间对车辙和模型黏弹性参数的影响规律，为沥青混合料的设计提供参考。研究结果表明：通过正交分析，对车辙深度的影响，温度的影响最大，作用时间次之，温度的影响程度是作用时间、荷载的2倍和10倍。温度、荷载和作用时间对于沥青混合料本构模型中的4个黏弹性参数(E1,η2,E3,η3)的影响各有不同：对参数E1的影响，作用时间分别是温度和荷载所对应值的1.6倍和4倍；对于参数η2的影响，温度影响为作用时间和荷载的1.5倍，而后两者的影响程度相当；对参数E3的影响，温度和荷载影响基本相同，两者是作用时间的2.5倍；对参数η3的影响， 荷载和作用时间对η3的影响差别不大，荷载和作用时间分别是温度的1.6倍和1.4倍。通过温度和作用时间的共同作用分析，高温和长作用时间共同作用是车辙变形急剧增大的主要原因。

关键词：沥青混合料; 黏弹性; 本构模型; 正交分析; 车辙

由于沥青混合料特有的黏弹性力学特性和外界影响因素的多样性，而沥青路面往往暴露在自然环境中，且环境复杂多变，使得公路在运营期间，路面结构强度不断降低，路面在一定时间内抗车辙性能变化非常大。国外在分析车辙变形的模型主要有Sousa的非线性黏弹性模型，Monismith的层应变车辙模型，F.Morea基于沥青低剪切黏性的LSV模型，以及国内徐世法的“四单元五参数”预估模型，张肖宁的线黏弹性广义Maxwell模型，茅梅芬的基于重复荷载作用下车辙和荷载作用次数之间的数学模型等[1-6]。研究车辙变形的模型有很多，但是从黏弹性力学并结合外界影响因素的角度研究车辙变形的方法基本没有，所以如何从黏弹性力学的角度定量分析影响车辙形成的外因和探讨它们与沥青混合料黏弹性参数之间的关系值得进一步探索，本文的研究能为沥青路面的设计提供参考。

1导致沥青路面产生破坏的外部因素

影响路面永久变形的外部条件有很多，主要包括温度、荷载以及荷载作用时间。由于沥青是一种成分比较复杂的无定形高分子化合物的混合物，其物理形态随温度的变化而显著变化，当沥青路面表面温度高于道路沥青的软化点温度时，在交通荷载的反复作用下将产生显著变形，其中部分变形不会随着卸载而消失，并残余下来成为永久变形[7-8]。在荷载应力大于沥青混合料的蠕变极限强度时，沥青路面将产生不可回复永久性变形[9]。沥青混合料的蠕变强度愈低，荷载应力愈大，愈容易形成蠕变变形。荷载作用时间与车速相关，低速的实质就是相当于增加了车辆作用时间。一般来说，行车速度愈慢，蠕变时间则逾长，更容易形成不可回复的蠕变变形。

2Burgers模型的选择

在黏弹性材料的的本构方程中，可以发现黏弹性材料的力学响应取决于松弛函数和蠕变柔量，而不同的模型具有不同的松弛函数和蠕变柔量，最简单的黏弹性模型由一个弹簧和一个阻尼器串联或并联而成，为别为Maxwell和Kelvin模型。但是这2个模型具有一定的局限性，而由这2个模型衍生出来的Burgers模型可以较好地描述黏弹性材料的蠕变与松弛特性[10-13]，在道路工程领域将其作为沥青混合料的本构模型有广泛的应用。该模型中串联有单个弹性元件，所以其具有瞬时弹性。同时该模型中串联有黏性元件，本构方程中包含应变对时间t的导数，模型在无限大时刻的变形产生黏性流动，变形可无限发展，且应力能够完全松弛。变形包括3部分：弹性变形ε1,黏流ε2和黏弹性变形ε3。E1,E3,η2和η3为Burgers模型4个黏弹性参数，分别为弹性剪切模量，控制延迟弹性的模量，黏滞流动的速率，控制延迟弹性的速率。Burgers模型如图1。

图1　Burgers 模型示意图Fig.1 Burgers model

其蠕变柔量J(t)为：

(1)

式中：τ=η3/E3。

3不同条件下沥青路面的力学参数分析

3.1正交试验方法方案设计

3.1.1影响因素的选择

由于沥青混合料的黏弹性性质，使得沥青路面在运营过程中，会受到车辆荷载、荷载作用时间和温度的影响。荷载应力愈大，愈容易形成蠕变变形。而且沥青黏度随荷载应力增大呈指数关系降低，因而变形量将随荷载应力增大而呈指数倍数关系增大；荷载作用时间与路面变形成非线性关系，一般荷载作用时间增大一倍，路面变形正大约1.4倍[7]。另外，根据时温等效换算原理，荷载的长时间作用将产生和高温条件同样的后果，长时间荷载的累积会使沥青混合料严重变形。当沥青路面表面温度达到40～50 ℃以上，高于道路沥青的软化点温度时，在交通荷载的反复作用下将产生显著变形，其中部分变形不会随着卸载而消失，并残余下来成为永久变形。本文在进行黏弹性力学分析中主要考虑温度、荷载及荷载作用时间。

3.1.2因素水平的确定

因素水平的确定，一般根据已有的经验或欲考察的变化幅度确定大致的范围，再从中选取范围的上下界和若干个中间插值作为因素水平。因素水平的确定应具有代表性，能客观反映实际和所要考察的情况。

为更好地考察每个因素的影响幅度，本文在研究时采用三因素三水平正交设计表。从实际情况考虑，温度考察范围为30～60 ℃，荷载范围为0.7～1.4 MPa。另外车辙试验速度为42次/min时，轮迹带上某点被作用一次时间就是0.130 s；速度为28 次/min时,作用时间为0.196 s；速度为14次/min时,作用时间为0.388 s，所以时间考察范围为0.130～0.388 s。见表1。

表1　因素水平

3.2计算方法的选择

在分析外界因素对沥青混合料黏弹性性能影响时，采用室内车辙试验进行模拟，考核指标为车辙深度(RD), 然后差分进化算法反算Burgers模型中的参数。差分进化(Differential Evolution,DE)算法是Rainer和Kenneth Price提出的一种采用浮点矢量编码在连续空间进行随机搜索的优化算法。其特点是：受控参数少，实施随机、并行、直接的全局搜索，易于理解和实现，目前被广大学者所采用[14-15]。

3.2.1广义虎克定理应力—应变关系

根据广义虎克定理：对于各向同性材料，小变形条件下，正应力引起线应变，剪应力引起相应的剪应变。 三向应力状态下应力与应变的张量关系为：

(2)

其中:δij为克罗内克符号。

沥青混合料车辙试件固定在钢质试模中，试件侧向完全限制，在X轴和Y轴方向的应变为0，可推导出：

(3)

由式(2)～(3)，可得：

(4)

又有波尔兹曼原理，得：

(5)

由式(4)～(5)，得：

(6)

3.2.2循环应力作用下单层车辙板永久变形响应

车辙试件所受的荷载为矩形荷载，考虑到车辙试验数据采集时是在轮载作用时间下，最后得到在荷载有效作用时间下蠕变公式为[11,16]：

(7)

同时根据应力分布扩散角法，确定沥青混合料的扩散角，一般取值为45°。由应力扩散原理，对于矩形试件计算公式如下[17]：

(8)

最后通过利用阶跃荷载原理和积分型本构方程，最后推导车辙深度与各黏弹性参数的关系如下：

(9)

式中：μ为泊松比；E1,E3,η2和η3为Burgers模型4个黏弹性参数；σ0为轮压，MPa；t0为某点碾压一次时荷载有效作用时间，s；T为车轮行走一次作用时间，s；t为某一时刻，s；H为车辙深度，mm。

3.3室内试验

3.3.1试验仪器

本实验采用新型车辙试验仪，该新型车辙试验仪具有结构简单、使用方便、可调节速度、可调节温度、可调节载荷大小、可记录试验全过程的车辙变形数据等优点，适合于研究沥青混合料抗车辙性能的室内车辙试验。

3.2.2混合料类型

很多研究表明，沥青混合料层的最大的剪应力出现在路表以下5～10 cm处，车辙也主要发生在此深度，也就是通常说的中面层。也有研究表明，在3层路面结构中，中面层的车辙贡献率大于上、下2个面层。因此对中面层的研究显得尤为重要。在国内，中面层混合料普遍使用的类型是AC-20。本次试验采用的沥青混合料为AC-20C，沥青采用重交A-70型号。沥青混合料级配曲线及沥青性质见图2和表2。

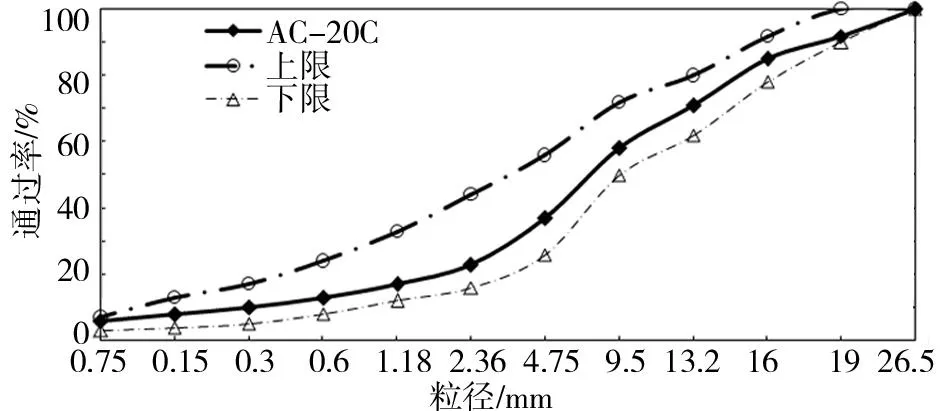
图2　沥青混合料AC-20C级配Fig.2 AC-20C asphalt mixture gradation curves

设计指标沥青A-70混合料AC-20C密度/(g·cm-3)1.0502.551针入度(0.1mm)66软化点/℃48最佳沥青用量/%4.2孔隙率/%3.7

3.4计算结果及分析

通过室内车辙试验得到试验结果RD，然后将公式(9)嵌入1stOpt软件中，采用改进差分进化法进行反算，最后得到Burgers模型4个参数E1，η2，E3和η3。温度60 ℃，荷载1.4 MPa,作用时间0.196 s的拟合曲线如图3所示，其中横坐标为时间，纵坐标为车辙深度。

图3　曲线拟合图Fig.3 Cuver fitting

从图3可以看出，拟合曲线和实测数据相关度较好，相关系数为0.998，所以该本构模型能够较好的描述车辙变形的过程，而且采用改进差分法进行拟合的曲线相关性较好，可以用来对黏弹性参数进行迭代反算。正交试验中的车辙及黏弹性参数计算结果如表3。

3.4.1直观分析

根据表4中的数据，对相对极差与各因素之间的关系进行分析，见图4。极差R的相对变化是以第1个值为1，其余值除以第1个值得到，作为数据坐标轴纵坐标。根据图4分析了温度、荷载和作用时间3因素对车辙深度RD以及Burgers四参数E1，η2，E3和η3的影响。

图4　各影响因素极差变化Fig.4 Variations of various factors

1)总的来说，各因素对车辙深度的影响，温度大于作用时间，而作用时间大于荷载。车辙深度极差变化曲线中，温度的极差变化分别是作用时间、荷载的2倍和10倍，作用时间是荷载的4倍。因此降低沥青混合料的温度敏感性，提高高温稳定性，并减少荷载作用时间是抵抗变形是最有效的途径。

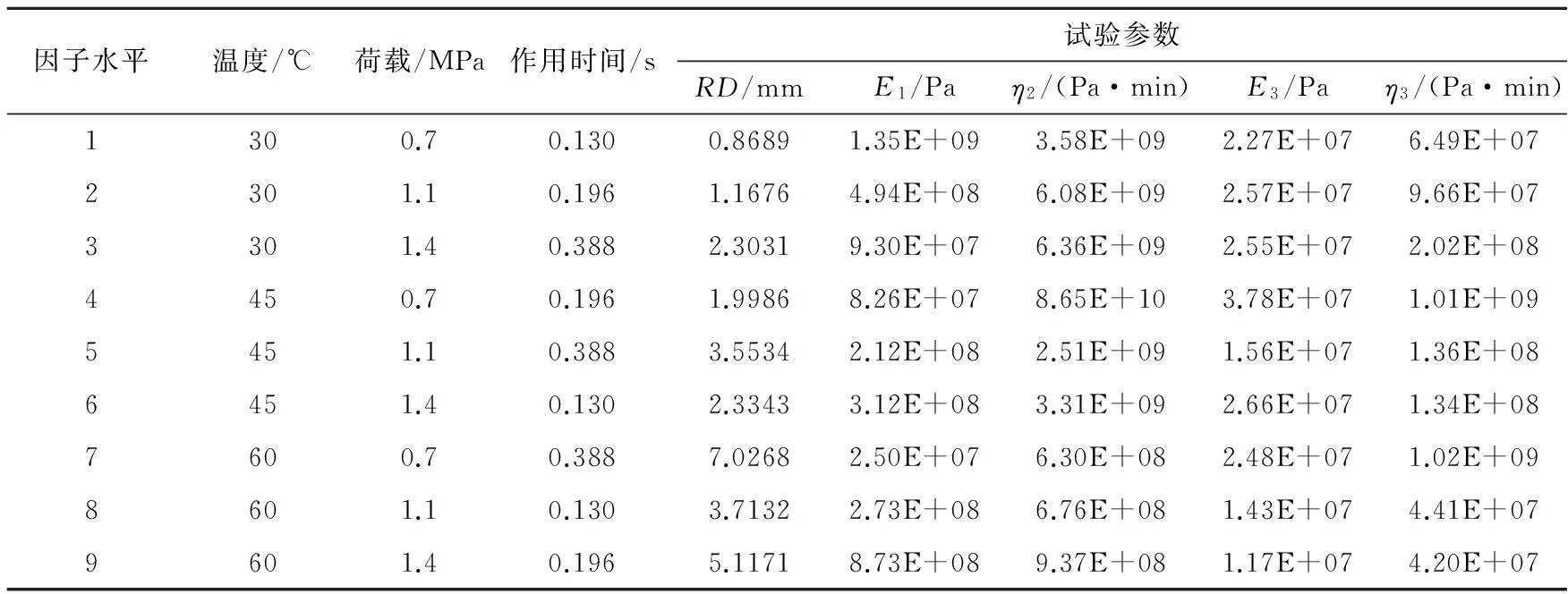
表3　车辙正交试验及计算结果

表4　正交试验分析结果

注：①T为对应的累加值，R为极差；② 黏弹性参数E1，η2，E3和η3采用10为底的对数值；③平均相关性为0.99。

2)从图中同样可以看出温度、荷载、作用时间3个因素对Burgers模型的四参数的影响各不相同：

①对参数E1的影响：作用时间>温度>荷载，其中作用时间的极差相对变化值分别是温度和荷载所对应值的1.6倍和4倍。因此要想增加E1值，主要是减少作用时间，其次是降低温度,最后才是减小荷载。

②对于参数η2的影响：温度影响最大，其中作用时间和荷载对η2的影响基本相同，温度影响为作用时间和荷载的1.5倍。因此，为了保持沥青混合料的较大的黏度，提高温度稳定性，主要通过降低路面温度的方法。

③对参数E3的影响：温度>荷载>作用时间，温度和荷载对E3的影响基本相同，而作用时间对其的影响相对较小，温度和荷载的影响程度是作用时间的2.5倍，这说明E3对作用时间不是太敏感。要增加对E3值的影响，可以从减小温度和荷载的角度考虑。

④对参数η3的影响，荷载>作用时间>温度，其中温度的影响最小，荷载和作用时间的极差变化值分别是温度所对应值的1.6倍和1.4倍。荷载和作用时间对η3值的影响差别不大。

3.4.2敏感性分析

根据正交试验分析结果表4，绘制出车辙深度、E1，η2，E3和η3参数相对变化与各影响因素增长水平之间的关系图(见图5～9)，分析结果如下。

图5　各影响因素水平与车辙深度关系Fig.5 Relationship between level of factors and rutting depth

图5表明，随着各影响因素水平的增长，车辙深度总体上是增加的。其中，温度对车辙深度的影响变化最为明显，作用时间的影响程度相对温度要小很多，而荷载影响程度变化最小。温度和作用时间随着因素水平的提高，其影响程度也不断挺高，后期影响程度明显大于前期。所以温度超过45°(沥青软化点附近)后，车辙深度变化率变大，所以要减少车辙深度，首先控制沥青混合料温度不超过软化点或者提高沥青软化点是合适的；其次，作用时间不宜过长，即保持较快的车速。同时，从图中可以看出，车辙随荷载因素水平的增加出现先减少后递增的现象，主要跟因素的组合作用有关，即在1.1 MPa荷载条件下，没有极端温度和作用时间的组合。

图6　各影响因素水平与E1对数值关系Fig.6 Relationship between level of factors and logE1

图6表明，E1对数值的相对变化受作用时间的影响最为明显，前期变化比较小，后期变化幅度较大。温度影响线变化呈v字型，在45 ℃前E1对数值递减，超过该温度值后递增。荷载对E1对数值的影响最小，整体上持平，变化幅度在9.2～9.0 Pa之间。所以要使E1对数值增大，主要是减少作用时间。

图7　各影响因素水平与η2对数值关系Fig.7 Relationship between level of factors and logη2

图7表明，温度和作用时间对η2对数值的影响程度基本一致，温度影响变化程度稍大于作用时间，荷载的影响程度在因素水平较小时，变化幅度大，而在因素水平较大时则变化较小。η2对数值在温度为45 ℃和作用时间为0.196 s时达到峰值，随后迅速减小，所以合理控制好温度和作用时间，能够增加沥青混合料的黏性，提高沥青混合料的高温稳定性。

图8　各影响因素水平与E3对数值关系Fig.8 Relationship between level of factors and logE3

图9　各影响因素水平与η3值关系Fig.9 Relationship between level of factors and logη3

图8表明，对于E3对数值的影响：温度和荷载影响程度变化幅度较大，作用时间的影响程度变化幅度较小，在7.8～7.9 Pa范围变化。温度影响程度在因素水平较小时变化幅度较小，反之则大，而荷载影响程度较温度相反。作用时间的影响变化幅度不大。E3对数值在温度为45 ℃和作用时间为0.196 s时达到峰值，而随着荷载的增加总体上是减小的。

从图9可以看出，荷载的影响程度最明显，在因素水平较小时变化最为显著，因素水平较大时则变化幅度较小。当荷载增加至1.1 MPa时，η3对数值降至最小值，而在温度为45 ℃和作用时间为0.196 s时，η3对数值增至最大。温度和荷载影响线类似，都是在因素水平较小时变化幅度较大，反之则变化幅度小。

4影响因素共同作用分析

外界影响因素对车辙变形的影响往往是耦合作用的，而温度和作用时间相对荷载对车辙变形的影响较大，因此本文针对温度和作用时间对车辙变形的影响进行共同作用分析，如图10所示。

图10　车辙深度与温度和作用时间的关系Fig.10 Relationship between rutting depth and temperature &loading time

从图10可以看出，随着温度和作用时间的增加，车辙深度有不同程度的增加。其中温度方向的增幅要大于作用时间方向的增幅，高温下的增幅要大于低温下的增幅，但是长作用时间和短作用时间增幅差别不大。同时可以看出，高温和长作用时间的耦合作用最明显，车辙变形深度最大达7.036 8 mm。而低温和短作用时间下的车辙变形深度只有0.868 9 mm,前者是后者的8倍。所以避免高温和长作用时间这种极端恶劣条件的共同作用，特别是避免高温，能有效减小车辙变形。

5结论

1)由Burgers模型推导出的单层沥青混合料车辙模型能够较好地模拟沥青混合料的黏弹性性能，通过多元外界条件下的车辙试验结果，能够轻易反算得到不同外界条件下该模型的4个黏弹性参数，从而可以进一步分析不同外界影响因素与该模型黏弹性参数之间的关系。

2)从正交试验直观分析表中可以得出：车辙深度极差变化曲线中，温度的影响大于作用时间，作用时间大于荷载。对参数E1的影响：作用时间大于温度，温度大于荷载。 对于参数η2的影响，作用时间和荷载对η2的影响基本相同，温度影响最大；对参数E3的影响，温度和荷载影响基本相同，作用时间影响最小；对参数η3的影响，温度影响最小，荷载和作用时间的极差变化值分别是温度所对应值的1.6倍和1.4倍。因此，降低沥青混合料的温度敏感性，减少作用时间，提高车速，对抵抗变形是最有效的途径。相比而言，荷载对车辙的影响较小。

3)在敏感性分析中，车辙主要是受温度和作用时间的影响，特别是当温度超过软化点后，影响程度明显加剧，对温度最为敏感。参数E1对数值的相对变化受作用时间的影响最为明显；η2对数值在温度为45 ℃和作用时间为0.196 s时达到峰值，随后迅速减小；E3对数值在温度为45 ℃和作用时间为0.196 s时达到峰值，而随着荷载的增加总体上是减小的；η3对数值受荷载影响程度最为明显。

4)从影响因素共同作用结果分析来看，极端外界因素的共同作用是造成车辙变形主要原因，要避免高温和长作用时间的共同作用。

参考文献：

[1] Sousa. Permanent deformation of aggregate mixes[R].Washington.DC:Strategic.Highway.Research.Program, National Research Program Council, Report. NO.SHRP-415, 1994.

[2] Monismith C L, McLean D B. Design considerationsfor asphalt pavements [M].Berkley University of California, 1971.

[3] Morea F, Zerbino R, Agnusdei J. Wheel tracking rutting performance estimation based on bitumen Low Shear Viscosity(LSCV), loading and temperature conditions [J]. Mater Struct, 2014; 47:683-92.

[4] 徐世法.沥青路面的的黏弹性力学分析与车辙预估[D].上海:同济大学道路与交通工程系，1988.

XU Shifa.Viscoelasticity mechanics analysis and rutting forecast of the asphalt pavement[D].Shanghai: Roads and Traffic Engineering of Tongji University, 1988.

[5] 詹小丽，张肖宁,王端宜，等.改性沥青非线性黏弹性本构关系研究及应用[J]. 工程力学,2009, 26(4):187-191.

ZHANG Xiaoli, ZHAGN Xiaoning, WANG Duangyi, et al. The modified asphalt nonlinear viscoelastic constitutive relation research and application[J]. Engineering Mechanics， 2009，26(4)：187-191.

[6] 茅梅芬.半刚性基层沥青路面车辙研究[J].华东公路，1995, 26(3)：45-49.

MAO Meifen. The research of asphalt pavement rutting on semi-rigid base[J]. East China Highway， 1995, 26(3)：45-49.

[7] 杨挺青. 黏弹性力学[M].武汉：华中理工大学出版社，1990.

YANG Tingqing. Viscoelastic mechanics[M].Wuhan: Huazhong University of Science and Technology Press,1990.

[8] 郑建龙.沥青路面温度收缩开裂的热黏弹特性研究[D].西安：长安大学，2001.

ZHENG Jianlong. Thermal viscoelastic properties of temperature shrinkage cracking of asphalt pavement [D]. Xi’an:Chang’an University, 2001.

[9] 刘立新著. 沥青混合料黏弹性力学及材料学原理[M].北京：人民交通出版社，2006.

LIU Lixin. Asphalt mixture principle of viscoelastic mechanics and material science[M]. Beijing: People's Traffic Press, 2006.

[10] Liu Yu, Feng Shirong, Hu Xiaguang. Dicrete element simulation of asphalt mastics based on burgers model[J]. Journal of Southwest Jiaotong University, 2007,15(1):20-27.

[11] 龙尧，谢晶，王德群,等.基于Burgers模型的沥青混合料室内车辙试验黏弹性分析[J].中外公路,2011,31(5):30-34.

LONG Yao, XIE Jing, WANG Dequn, et al. Viscoelastic analysis of laboratory rutting test of asphalt mixture base on Burgers model [J].Journal of China & Foreign Highway, 2011,31(5):30-34.

[12] 康永刚,张秀娥.基于Burgers 模型的岩石非定常蠕变模型[J].岩土力学,2011,32(增1):424-427.

KANG Yonggang, ZHANG Xiuer.Based on the Burgers model of the unsteady rock creep model[J]. Rock and soil mechanics,2011,32(Suppl 1):424-427.

[13] Huilin Lai, Changfeng Ma. A new lattice Boltzmann model for solving the coupled viscous Burgers’ equation [J].Physica A, 2014,395: 445-457.

[14] Rainer S, Price K. Differential evolution- a simple and efficient heuristic for gloabal optimization over Continuous Spaces[J]. Journul of Global Optimization,1997,11(4): 341-359.

[15] Price K. Different evolution a fast and simple numerical optimizer[C]// 1996 Biennial Conference of the North American Fuzzy Information Processing Society. New York, 1996, 524-527.

[16] 龙尧.沥青混合料车辙实验及黏弹性分析[D].长沙：长沙理工大学，2010.

LONG Yao. Asphalt mixture rutting test and viscoelastic analysis [D]. Changsha: Changsha University of Science and Technology.2010.

[17] 高大钊,袁聚云.土质学与土力学[M].北京:人民交通出版社,2003:56-94.

GAO Dazhao,YUAN Juyun. Soil mechanics[M]. Beijing: China Communications Press, 2003:56-94.

Research on asphalt mixture viscoelastic parameters under different conditionsPENG Dongli1, ZHANG Jiasheng2， LONG Yao2

(1. School of Engineering Economy, Hunan Communication Polytechnic, Changsha 410132, China;2.School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract:Through the rutting test under different conditions and constitutive model of asphalt mixture(AC-20C) with cyclic stress, the impact of temperature, stress and loading time on rutting deformation and viscoelastic parameters were researched, which can provide a reference for design of asphalt mixture. Through the orthogonal analysis, the test results show that temperature has the most important impact on rutting, while loading time play a secondary role. The influence degree of temperature is 2 and 10 times of loading time and stress, respectively. Meanwhile, the impact of temperature, loading time and stress on viscoelastic parameters(E1,η2,E3,η3) of the constitutive model are different. The impact of loading time on the E1 is 1.6 and 4 times than that of temperature and stress, respectively. Then the impact of temperature on η2 is found to be 1.5 times than loading time and stress. As for the E3, the impact of temperature and stress are mostly similar which are 2.5 times than that of loading time. Finally, the impacts of stress and loading time are 1.6 and 1.4 times than that of temperature, respectively. Through the analysis of combining impact of temperature and loading time, the main reason for the enormous increase of rutting deformation is the combined effect of higher temperature and longer loading time.Key words： asphalt mixture; viscoelasticity; constitutive model; orthogonal analysis; rutting

中图分类号：U416.217

文献标志码：A

文章编号：1672-7029(2016)04-0689-08

通讯作者：张家生(1964-),男，湖南怀化人，教授，博士，从事岩土工程研究；；E-mail:jszhang_csu@vip.163.com

基金项目：国家自然科学基金资助项目(51378514)

收稿日期：2015-08-04