简支铁路箱梁与轨道结构温度场仿真分析

刘柯，戴公连，朱乾坤

(1. 天津市政工程设计研究院，天津 300051；2. 中南大学 土木工程学院，湖南 长沙 410075)



简支铁路箱梁与轨道结构温度场仿真分析

刘柯1，戴公连2，朱乾坤1

(1. 天津市政工程设计研究院，天津 300051；2. 中南大学 土木工程学院，湖南 长沙 410075)

摘要:针对目前我国高速铁路中普遍采用的32 m简支箱梁与CRTS II型无砟轨道结构，基于传热学基本理论，考虑太阳辐射与对流换热，采用ANSYS有限元软件建立箱梁-无砟轨道温度场仿真分析模型，分析整个结构在典型时刻的温度分布特征，并研究无砟轨道板、箱梁顶板、腹板和底板等典型位置处的温度随时间变化规律。基于温差最大时刻的结构温度分布，根据温度场数值仿真模型计算结果，拟合得到无砟轨道结构和无遮盖部分箱梁的竖向温度梯度分布模式，可为我国典型地区CRTS II型无砟轨道的温度应力计算提供参考。

关键词：高速铁路；混凝土箱梁；无砟轨道；温度场；仿真分析

近年来，国内外学者对大跨径预应力混凝土连续梁、连续刚构桥病害进行了深入研究，而箱梁竖向温度梯度效应越来越受到重视。大量理论分析和试验研究证明，在大跨度预应力混凝土箱形梁桥中，温度应力甚至可以超过活载引起应力[1]。对于铁路简支箱梁，目前,国内外对其温度效应已有较为深入的研究，但之前的研究均忽略了轨道板对桥梁温度分布的影响，过去的研究习惯于把桥梁截面作为一个单独的研究对象来分析[2-4]。但铁路桥梁尤其是高速铁路桥梁上基本上都铺设有无砟轨道，因此研究桥梁结构和轨道板共同的温度场分布显得十分必要。本文以江西南昌地区高速铁路标准32 m简支箱梁为工程背景，对铺设CRTS II型板式无砟轨道结构的日照温差模式进行仿真分析研究，讨论箱梁与轨道板结构温度分布模式，并与国内外相关规范进行对比，为铁路箱梁结构温度应力的计算提供部分依据。

1温度场仿真模型

1.1工程背景

CRTS II板式无砟轨道具有高平顺性、维修少和维修天窗短等特点，在我国京津城际、京沪和沪昆等客运专线上得到了广泛应用。其结构组成主要包括混凝土底座、CA砂浆填充层和双向预应力轨道板。桥上CRTS II无砟轨道结构尺寸参数见图1，其中混凝土底座板宽2.95 m，高0.3 m，CA砂浆填充层宽2.55 m，高0.05 m，轨道板宽2.55 m，高0.2 m，线间距取值为5.0 m。本文温度场仿真模型计算气候参数根据江西南昌地区气候条件选取。

图1　桥上CRTS II型无砟轨道Fig.1 Ballastless track structure on the bridge

1.2有限元模型的建立

由于物体内部的温度通常只与空间位置坐标和时间有关，其任意点的温度可以由式(1)表示。

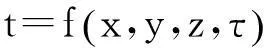
(1)

式中：t为温度；x,y,z为空间三维坐标；τ为时间[5]。

从理论上讲，混凝土箱梁的结构温度场是一个三维不稳定温度场，假定混凝土材料各个方向同性、均质，且符合线弹性假定，根据傅立叶定律，可得无内热源三维稳定热传导方程：

(2)

由于桥梁一般为狭长结构，可近似地认为桥梁纵向温度分布相同，而不考虑温度沿桥面纵向分布的变化，且将太阳光看成是平行射向地球，则三维热传导问题简化为二维热传导问题求解，且假设如果物体内部不向外传递热量，则式(2)可进一步简化为：

(3)

为了确定需要的温度场，还必须引入初始条件和边界条件，初始条件是初始瞬时物体整个区域中所具有的温度已知值，可以根据实际情况假定。

箱梁外表面总的边界热交换包括太阳辐射qs，对流换热qc及长波辐射qr这3项之和(见图2)，规定热流从外界流入结构为正、流出为负，传热边界条件可写为：

(4)

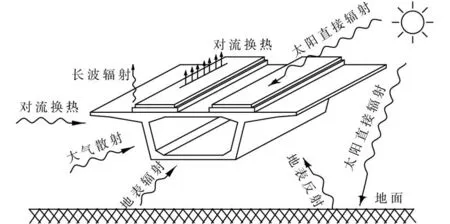
图2　桥梁与外界的各种热交换Fig.2 Heat exchange between bridge and outside

混凝土表面所能吸收到的太阳辐射qs包括有太阳直接辐射、天空散射和地表反，但其并不能将辐射到表面的太阳能全部吸收，若表面吸收短波辐射的能力以短波辐射吸收率at表示，则:

qs=atIt

(5)

式中：It为太阳直接辐射、天空散射和地表反射强度的总和。

对流换热qc可表示为[6]

qc=h(Ta-T)

(6)

其中h为对流交换系数，采用Jurges-Nusselt公式进行计算。

长波辐射qr根据Stefen-boltzman辐射定律可按下式计算[7]：

qr=εC0[(273+Ta)4-(273+T)4]

(7)

式中：εa为辐射率；C0为Stefen-boltzman 常数。本文采用ANSYS的热分析功能来实现桥梁的日照温度场分析。温度场按平面有限元分析，有限元的最小尺寸为0.03 m，采用PLANE55单元，分析模型有1 258个单元，1 130个节点，如图3所示。

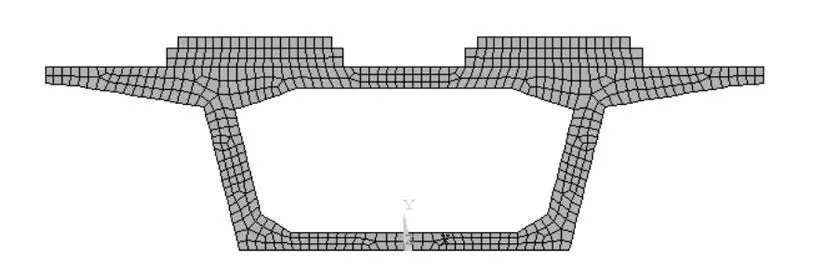
图3　CRTS II型板式轨道温度计算有限元模型Fig.3 Temperature finite element model of CRTS II type ballastless track

模型中将各个表面的热边界条件转化为综合的热流密度施加到箱梁表面上面。混凝土箱梁的热边界条件包括各表面与箱内空气的对流换热和辐射换热，过程较复杂，但过去研究表明，箱梁内部空气1 d内温差变化不大，且高于平均温度1.5 ℃左右，故本文忽略箱内空气和混凝土箱梁内壁之间的辐射换热，将箱梁内部空气作为一种热的不良导体，并赋予其初始温度，初始温度按高于箱梁混凝土初始温度1.5 ℃考虑[8-10]。

在非稳态分析中，往往需要一个渡越时间来消除初始值对计算结果的影响，本文对混凝土箱型截面的分析时长为10 d，通过前6 d的循环计算消除了初始值对计算结果的影响[5]。

1.3模型验证

为验证数有限元模型的可靠性，对比数值模拟结果与实测数据，见图4。温度实测工点为江西南昌高铁简支桥梁，所测数据为2014-02,10 d内桥上还未铺设高铁时箱梁的温度。从图中可以看出，数值模拟计算结果与实测值变化趋势一致，吻合较好，有限元模型结果满足工程精度。

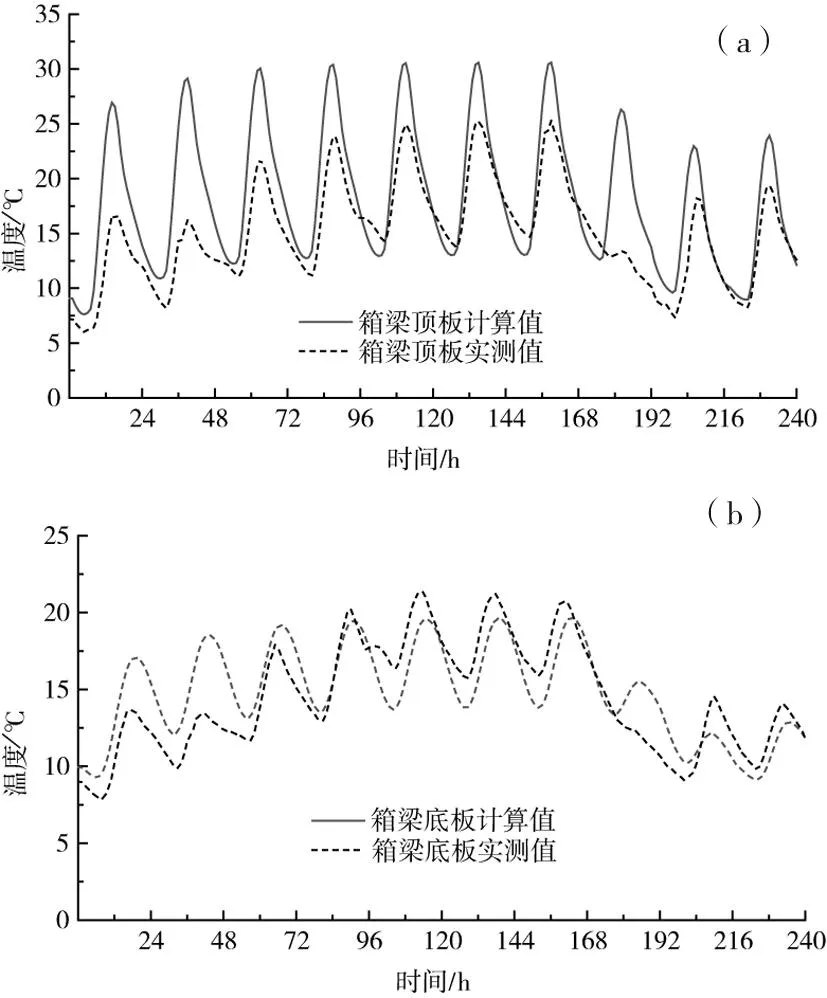
图4　计算值与实测值对比Fig.4 Comparison of calculated and measured results

2箱梁及无砟轨道结构温度分布特征

2.1温度分布规律

在计算时长最后一天的各个关键时刻，铁路箱梁及CRTS II型无砟轨道板截面温度场分布见图5，图中未显示箱梁内部空气温度。白天由于外界气温的逐渐升高和受到太阳辐射作用，混凝土箱梁的表面以及轨道板表面的温度迅速增长，到了14∶00，外表面温度明显高于混凝土内部温度，形成正温差。但到了接近傍晚时刻，外界温度降低，混凝土表面温度较快的降低，但由于混凝土是热的不良导体，内部温度向外部传热缓慢，导致结构内部温度高于表面温度，形成负温差。从温度云图可以明显的看出，直到第2天早上的6∶00，内部温度还明显高于外部温度，温度分布不均匀。

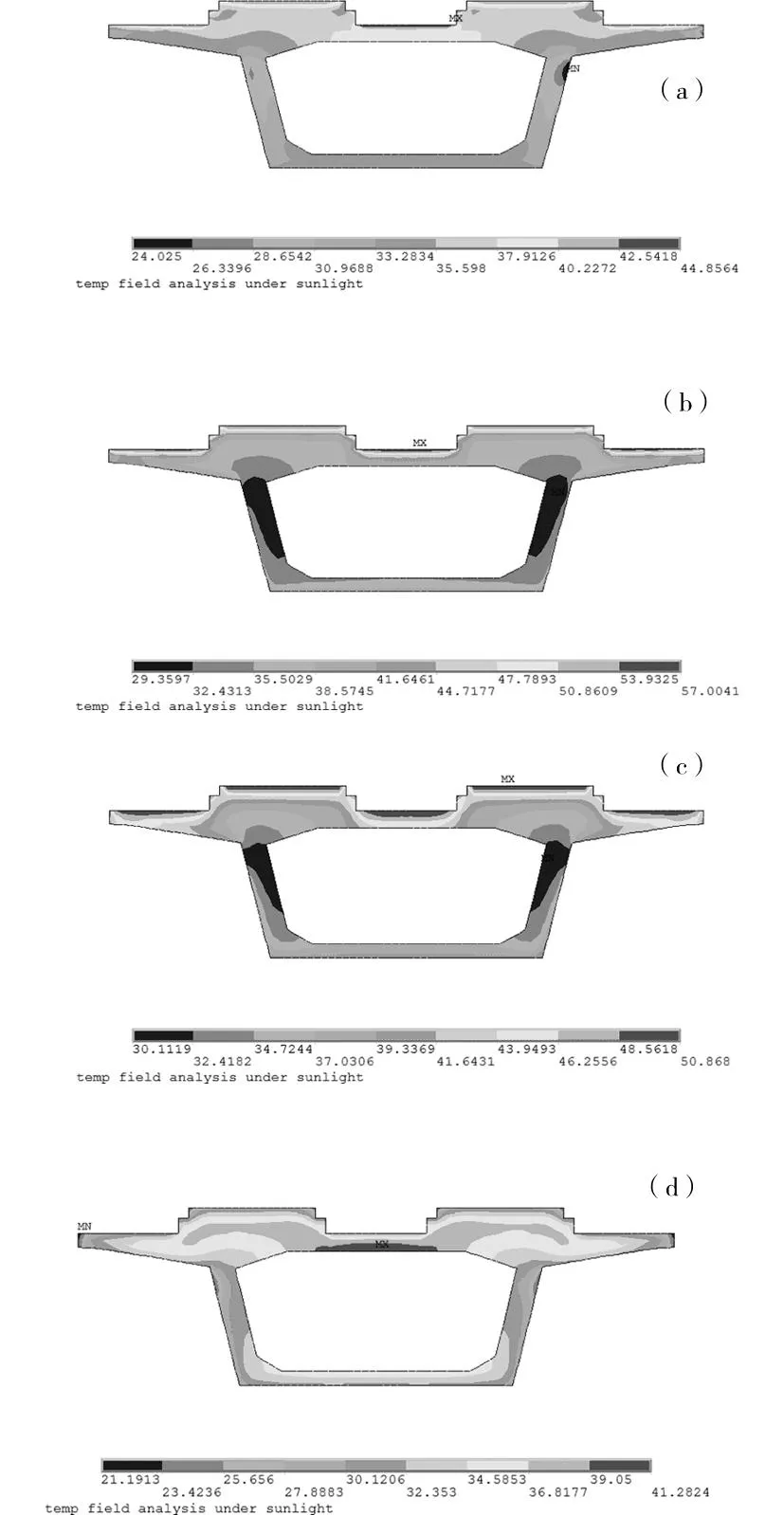
(a) 10∶00 (第1 d);(b)14∶00 (第1 d); 18∶00 (第1 d)；(d)06∶00 (第2 d)图5　CRTS II型箱梁截面关键时刻温度云图Fig.5 Contour of girder section’s temperature at key points

为了得到箱梁各部位温度的日变化过程，选择了分析截面中的关键点，关键点编号如图6中所示，其温度日变化历程曲线见图7。

图6　箱梁关键部位温度点示意图Fig.6 Key points for the box girder

(a)T1,T2和T3；(b) D1，D2和D3；(c) G1，G2和G3G4；(d) F1，F2和F3图7　关键点时间-温度曲线Fig.7 Temperature-time curve of key points

比较图6中各图可知，箱梁底板温度变化幅度(图6(b))相对于顶板(图6(a))明显减小；没有轨道板遮盖的箱梁顶板(图6(a))温度变化幅度与轨道板(图6(c))温度变化幅度基本一致，这2个地方温度变化最为剧烈；另外，箱梁腹板(图6(d))外侧的温度变化幅度较腹板内侧也明显要大。总体而言，结构内部温度相对于结构表面温度的波动表现出有明显的滞后关系，这是混凝土的导热性能差的特点导致的；从而导致了整个结构温差的出现。

3温度模式讨论

为进一步研究CRTS型板式无砟轨道结构(包括轨道板和底座板)及箱梁温度竖向分布情况，本文主要基于标准日下午15∶00 (该时刻温差最大)箱型截面的温度分布，对轨道结构和箱梁竖向温差的曲线进行分析，提出适用于简支箱梁上CRTS II板式无砟轨道的温度模式。

3.1轨道结构温度模式

综合各国规范关于混凝土结构的竖向温度梯度的相关规定可知，结构的温度梯度分布主要在距顶板(或底板)边缘50和75 cm范围以内，多以非线性分布，本文考虑温度梯度分布主要在50 cm以内。

轨道结构的温度荷载模式按以下2方面考虑：1) 由于底座板底面温度最低，故将该处温度作为整体温度加载至整个系统上，既系统整体升温；2) 其余部分温度与该处温度差值单独作为温差分别加至各个部分，即温度梯度。

在15:00时刻，轨道板顶面最高温度为56.14 ℃，底座板底面最低温度为36.53 ℃，温差为16.61 ℃。通过对数据的整理和拟合，轨道结构竖向温度梯度分布拟合曲线，拟合结果如图8所示为：

Ty=21.27e-6.34y

(8)

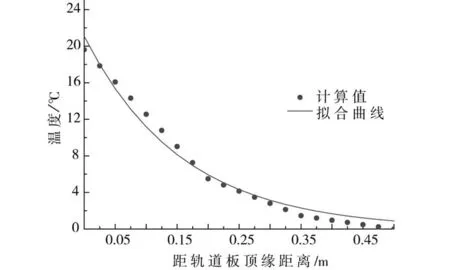
图8　轨道板竖向温差拟合结果图Fig.8 Vertical temperature difference of track slab

3.2箱梁温度模式

与轨道结构类似，箱梁的温度荷载加载模式可按以下考虑：1) 箱梁底板上缘处温度最低，将该处温度作为整体温度加载至整个系统上，既系统整体升温；2) 其余部分温度与该处温度差值单独作为温差分别加至各个部分，即温度梯度。

在15:00，截面中心处顶板最高温度为57.3 ℃，底板最高温度为41.1 ℃，箱梁最低温度处为底板上缘，为35.6 ℃，所以箱梁截面整体升温考虑为35.6 ℃，将数据点分为2顶板与底板2部分来分别拟合，分段点为竖向正温差曲线拐点，即在底板上缘的位置。对于顶板温度梯度，采用了规范既有的曲线模式拟合，但对于底板的温度梯度，并未采用已有规范的线性拟合，仍然采用指数拟合，其中顶板和底板温度梯度拟合结果分别见式(9)～(10)，拟合结果与计算值分别见图9～10，从图中可以看出，拟合效果较好。

Ty=21.07e-3.56y

(9)

Ty=5.81e-9.69y

(10)

图9　箱梁顶板竖向温差拟合曲线图Fig.9 Vertical temperature difference of girder’s top plate

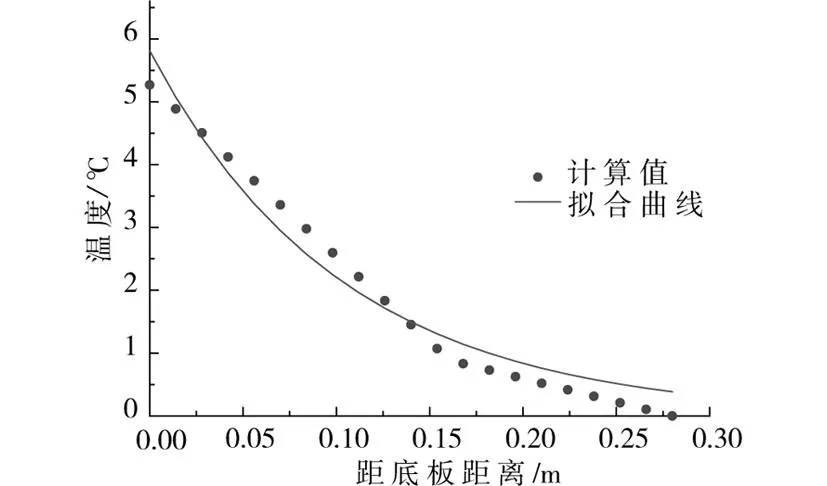
图10　箱梁底板竖向温差拟合曲线图Fig.10 Vertical temperature difference of girder’s floor

4结论

1)由于混凝土导热性能差，使得混凝土内部温度相对于混凝土表面温度表现出明显的滞后性，从而导致箱梁顶板、底板和腹板各部分以及轨道板存在正温度梯度和负温度梯度。

2)基于仿真模型计算结果，分析了桥上CRTS II型无砟轨道结构轨道板、底座板竖向温度梯度分布规律，并提出了相应计算模式。

3)在有轨道板遮挡部分，箱梁的顶板竖向温度梯度明显减小；箱梁顶板最大竖向温度梯度发生在没有轨道结构遮挡部分，本文计算结果表明，其温度分布规律与国内外规范基本一致。

4)由于无砟轨道结构的遮挡效应，导致箱梁在有遮挡和无遮挡位置处存在的横向温度梯度，还需进一步研究。

参考文献:

[1] 刘柯. 高速铁路桥梁结构温度场特性研究[D]. 长沙: 中南大学, 2014.

LIU Ke. The characteristics of temperature field on high speed railway bridge[D]. Changsha: Central South University, 2014.

[2] 刘兴法. 混凝土结构的温度应力分析[M]. 北京:人民交通出版社, 1991.

LIU Xingfa. Temperature stress analysis for the concrete structure[M]. Beijing: China Communications Press, 1991.

[3] 王森荣, 孙立, 李秋义, 等. 无砟轨道轨道板温度测量与温度应力分析[J]. 铁道工程学报, 2009(2): 52-55.

WANG Senrong, SUN Li, LI Qiuyi, et al. Temperature measurement and temperature stress analysis of ballastless track slab[J]. Journal of Railway Engineering Society, 2009(2): 52-55.

[4] 杨义礼. 土质路基上CRTS I型板式轨道温度力研究[D]. 兰州: 兰州交通大学, 2012.

YANG Yili. CRTS I plate rail temperature force on the soil subgrad[D]. Lanzhou: Lanzhou Jiaotong University, 2012.

[5] 彭友松. 混凝土桥梁结构日照温度效应理论及应用研究[D]. 成都: 西南交通大学, 2007.

PENG Yousong. Studies on theory of solar radiation thermal effects on concrete bridges with application[D]. Chengdu: Southwest Jiaotong University, 2007.

[6] 凯尔别克.太阳辐射对桥梁结构的影响[M]. 北京:中国铁道出版社, 1981.

Kehlbeck. The influence of solar radiation on the bridge structure[M]. Beijing: China Railway Publishing House, 1981.

[7] 戴公连, 郑鹏飞, 闫斌. 日照作用下箱梁桥上无缝线路纵向力研究[J]. 浙江大学学报, 2013, 47(4): 609-614.

DAI Gonglian, ZHENG Pengfei, YAN Bin. Longitudinal force of CWR on box girder under solar radiation [J]. Journal of Zhejiang University, 2013, 47(4): 609-614.

[8] Fu H C, Ng S F, Cheung M S. Thermal behavior of composite bridges[J]. Journal of the Structural Engineering. ASCE, 1990, 116(12): 3302-3323.

[9] 杨俊斌, 刘学毅, 梁东,等． CRTS I型轨道板中部砂浆离缝对轨道竖向变形与受力研究[J]. 铁道标准设计, 2013(6): 22-24．

YANG Junbin, LIU Xueyi, LIANG Dong, et al. The influence on track vertical deformation and stress state causedby seamed mortar layer in the middle of CRTS I track slab[J]. Railway Standard Design, 2013(6): 22-24.

[10] Baker C J, Chapman L, Quinn A, et al. Climate change and the railway industry: a review[J]. Proceedings of the Institution of Mechanical Engineers Part C, Journal of Mechanical Engineering Science, 2010, 224(C3): 519-528.

Simulation analysis of temperature field of simply-supported railway box girder and track structure

LIU Ke1, DAI Gonglian2, ZHU Qiankun1

(1. Tianjin Municipal Engineering Design & Research Institute, Tianjin 300051,china;2. Scool of Civil Engineering, Central South University, Changsha 410075, China)

Abstract：In view of the 32 m simply-supported box girders and the CRTS II type ballastless track structure which have been largely adopted in the high-speed railway in China, the box girder-ballastless structure simulation analysis model was established through the ANSYS finite element software. The model was based on the heat transfer theory, and the solar radiation and the convection heat transfer have been taken into consideration as well. The structure temperature distribution characteristics at typical time were analyzed in this paper. In addition, the temperature changing law with time at the positions including the ballastless track slab, box girder’s top plate, web and bottom plate was studied. Based on the structure temperature distribution when the temperature difference is largest and according to the calculation results, the vertical temperature modes of the ballast structure and the box girder have been presented, which could provide some useful information for the temperature stresses calculation of the CRTS II type ballastless track in the typical region.

Key words：high speed railway; concrete box girder; ballastless track; temperature field; simulation analysis

中图分类号：U448.21+3

文献标志码：A

文章编号：1672-7029(2016)04-0613-06

通讯作者：戴公连(1964-)，男，河南夏邑人，教授，博士，从事梁轨相互作用研究；E-mail：daigong@vip.sina.com

基金项目：国家自然科学基金资助项目(51378503)；高速铁路基础研究联合基金资助项目(U1334203)

收稿日期：2015-08-04