时速250 km/h铁路双线箱梁的畸变效应研究

蔺鹏臻，孙理想，冀伟，杨子江

(兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070)



时速250 km/h铁路双线箱梁的畸变效应研究

蔺鹏臻，孙理想，冀伟，杨子江

(兰州交通大学 甘肃省道路桥梁与地下工程重点实验室，甘肃 兰州 730070)

摘要:为了分析时速250km/h铁路32m跨度双线标准箱梁的畸变效应，基于板壳有限元建立了畸变效应分析的数值模型。采用板壳有限元方法和传统解析方法，对比计算仅单线活载作用下的畸变应力分布规律。通过定义翘曲比例系数，研究高跨比、宽跨比和壁厚等设计参数对畸变应力的影响规律。研究结果表明:与传统解析解比较，板壳有限元法更适合于箱梁畸变效应的分析。单线活载偏心作用下，跨中截面箱梁顶板靠近翼缘板边缘部位的翘曲比例系数可达11.6%；腹板与底板相交处翘曲比例系数最大，可达13.9%。跨中和l/4截面的翘曲比例系数ξ分析表明，现有箱梁设计参数合理，跨中最大翘曲比例系数小于15%，而l/4截面基本为0。箱梁高跨比、宽高比、壁厚等设计参数对畸变效应均有一定影响，总体规律是畸变效应随高跨比、宽高比和壁厚的增大而减小。

关键词：铁路箱梁；畸变；翘曲应力；数值分析

客运专线铁路与我国既有铁路相比, 具有速度高、对线路平顺性要求高等特点, 要求其桥跨结构具有较大的抗弯和抗扭刚度, 整孔双线简支箱梁由于受力简单、明确、形式简洁、外形美观、抗扭刚度大，建成后的桥梁养护工作量小以及噪音小等优点, 在许多国家的高速铁路建设中得到了广泛应用[1-2]。对双线铁路箱梁而言，当仅有单线运行列车时，列车活载相当于箱梁整体纵轴线的偏心荷载，将引起桥梁的扭转和畸变[1-2]。目前国内现有设计规范中[3-4]，基于箱壁较厚或横隔板较密的前提假设，认为箱梁畸变应力所占比例较小，设计中忽略畸变应力计算。但随着桥梁建设中双线铁路箱梁的出现、仅在梁端设置横隔板以简化构造和方便施工等趋势的发展，箱梁畸变产生的条件发生了变化，需要分析新时期箱梁结构的畸变效应规律。对于箱形梁畸变的分析，常用的方法有解析法和有限元法2种[1]。解析法将作用于箱形梁截面上的偏心荷载根据等效荷载思想分解成对称荷载与反对称荷载，对称荷载作用时按梁的弯曲理论求解；反对称荷载作用时根据薄壁杆件扭转理论分解为刚性扭转和畸变两种荷载模式的叠加[5]。畸变应力的解析计算方法，较为常见的分析方法有基于弹性地基梁的比拟法[6-7]和广义坐标法[8]。解析法通常首先确定畸变荷载，进而根据解析方程求得畸变引起的纵向翘曲正应力、剪应力和横向弯曲应力，计算过程较为繁琐。有限单元法基于三维板壳和块体理论，建立箱梁结构精细的三维有限元数值分析模型，施加箱梁边界和畸变荷载，求解获得畸变应力，是当前结构精细化分析的通用和便捷方法。Ghani等[9]应用板壳有限元模型，研究了横隔板和几何特征对钢箱梁畸变效应的影响。本文以时速250 km/h客运专线32 m标准跨度双线简支梁为研究对象，通过有板壳限元法数值模拟，研究箱梁的畸变效应。

1畸变效应分析模型

1.1箱梁基本参数

时速250 km/h客运专线32 m标准跨度简支箱梁跨中截面如图1所示。桥梁设计标准为双线，线间距4.6 m。轨道结构采用双块式无砟轨道，桥面板上直接铺设无砟轨道底座板。活载纵向采用ZK标准活载。梁体为C50混凝土，弹性模量按规范取值E=3.55×104MPa。

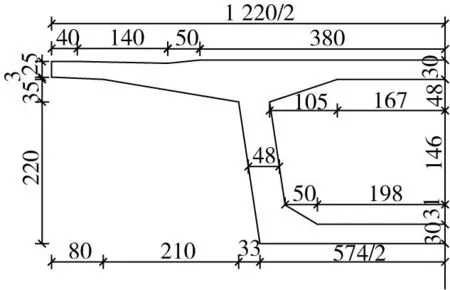
单位:cm图1　箱梁跨中截面Fig.1 Box girder section of mid-span

1.2有限单元模型

数值分析模型采用ANSYS软件SHELL63板壳单元模拟混凝土箱梁。由于本文主要分析箱梁弹性阶段的畸变效应，因此建模不考虑钢筋的影响。有限元模型如图2所示，模型边界条件按照简支梁受力模式施加。

(a)横截面；(b)空间透视图2　有限元模型Fig.2 Finite element model

1.3荷载施加

畸变效应是箱梁空间复合受力中的一种变形模式。当箱梁横截面上作用有偏心距e的荷载ΣP时，如图3(a)，根据截面荷载等效原则[4]，可分解为3种独立的变形模式：竖向弯曲，如图3(d)；刚性扭转，如图3(e)；畸变，如图3(f)。

双线铁路箱梁只有双线列车完全同步行进时符合对称受力特点，事实上这种完全对称的情况非常少见。因此上双线铁路在运营中绝大多数时候都会存在偏心活载作用，特别是当仅单线通过列车时偏心力矩最大。

根据现有设计规范[11]，客运专线铁路设计采用ZK活载，冲击系数取为1.08。对双线铁路箱梁，根据规范应该按照特种活载计算畸变效应。仅单线活载作用时由于偏心作用会产生梁体畸变效应，如图4所示。

由图3荷载分解方式，依据畸变荷载分解原理[4-5]，可确定出单个特种活载集中力引起的畸变荷载为：

(1)

(2)

(3)

在图2模型中，通过在研究的最不利位置施加式(1)～(3)计算获得的畸变荷载，进行求解后得到的纵向应力，即为畸变翘曲应力。

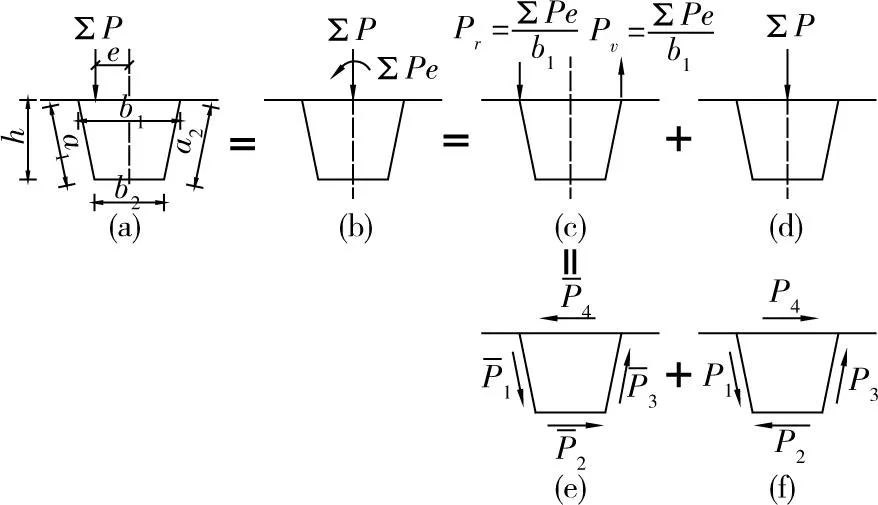
图3　偏心荷载的分解Fig.3 Decomposition of eccentric load

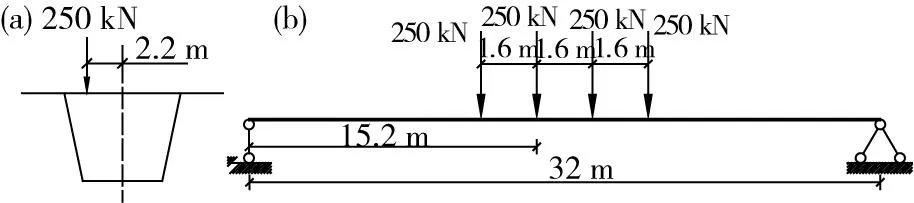
(a)横向；(b)纵向图4　加载示意图Fig.4 Schematic diagram of loading

2铁路箱梁畸变翘曲应力数值解与理论解对比

2.1跨中截面的畸变效应

对上述的箱梁，计算仅单线活载最不利(按特种活载布置在跨中位置)作用时，单线偏心活载由于畸变产生翘曲正应力。同时，采用传统畸变效应计算的解析方法[4-5]，计算相应的翘曲纵向正应力，与板壳有限元解进行对比，结果如图5所示。

从图5可以看出，基于板壳的有限元解与传统解析解在数值大小和变化趋势方面均较为接近，表明有限元方法可以模拟箱梁空间力学特性中的畸变效应。由于传统解析解是建立在理想的一维欧拉梁理论上的解析方法，应力结果为理想直线规律，这与实际箱梁空间受力特性存在一定偏差。通过板壳有限元方法，可以反映出箱梁空间板系受力特点，其结果更为真实可靠。

注：括号外为板壳有限元解，括号内为理论解析解单位：kPa图5　跨中截面翘曲应力分布Fig.5 Warping stress distribution on mid-span section

应力结果表明，箱梁在单线活载作用下，跨中截面腹板与底板连接点部位的畸变翘曲应力数值大于截面其余部位，表明对客运专线双线箱梁，边腹板和底板相连部位是畸变效应最突出的部位。

2.2铁路箱梁跨中截面畸变翘曲应力分析

为了比较双线箱梁翘曲应力的相对大小，引入翘曲比例系数ξ，其表达式为：

(4)

式中：σdw为计算点在偏心活载下产生的畸变翘曲纵向应力；σz为单线活载产生的包括畸变翘曲在内的总的纵向应力。可以看出，翘曲比例系数反映活载畸变效应产生的纵向正应力占总的正应力的百分比。

为了反映箱梁截面上不同部位的畸变程度，将箱梁跨中截面顶板、底板、腹板沿各自板块均匀分成10等份,分析翘曲比例系数ξ的规律，结果如图6所示。

从图6中可以看出，双线铁路箱梁在仅单线活载最不利作用时，跨中截面顶板及底板的翘曲比例系数ξ越远离截面中心越大，且沿板箱梁中线向两侧近似线性增大，顶板翘曲比例系数略大于底板。腹板的翘曲比例系数整体大于顶、底板，这是由于腹板以主要传递剪应力为主，因此式(1)中分母较小，故数值偏大。

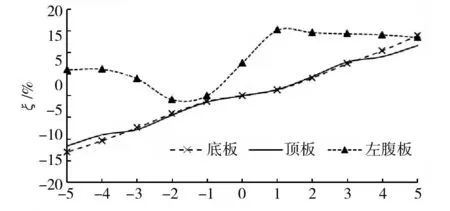
图6　跨中截面翘曲比例系数ξFig.6 Distortion ratio on mid-span section

数值表明，翘曲比例系数ξ最大的点为：1)顶板翼缘板端部，翘曲比例系数ξ最大达11.6%；2)腹板与底板相交处，翘曲比例系数ξ最大达达13.9%。3)腹板上靠近截面形心位置处，翘曲比例系数ξ最大达15.1%。

3设计参数对畸变翘曲比例系数ξ的影响

3.1高跨比对翘曲比例系数ξ的影响

高跨比(h/l)是箱梁重要的设计参数之一。以图1所示客专双线箱梁为例，进一步研究高跨比变化对畸变效应的影响。结合前述分析，选择箱梁截面上畸变效应突出的3个点，作为应力分析控制点：

1)1号点，位于左腹板与底板的交界部位;

2)2号点，位于左腹板与顶板的交界部位;

3)3号点，位于顶板翼缘板悬臂端部。

计算中，以32 m标准跨度为参照，通过改变桥梁跨度l，实现高跨比的改变。不同高跨比情况下，跨中截面和l/4截面的三个控制点部位的翘曲比例系数ξ的分布规律如图7所示。

(a)跨中截面；(b)l/4截面图7　高跨比对翘曲比例系数ξ的影响Fig.7 Effect of high span ratio on distortion ratio

从图7(a)中可以看出，跨中截面3个点的翘曲比例系数ξ随高跨比的增大近似呈线性增大，反映出箱梁跨度越小，畸变效应越突出。由曲线斜率可以看出，3号点部位、即顶板悬臂端部的畸变效应受高跨比影响最为突出，其次为1号点，2号点的畸变随高跨比变化较小。

从图7(b)中可以看出，l/4截面的畸变效应总体上小于跨中截面。l/4截面1号点和3号点随高跨比增大时翘曲比例系数ξ增大，而2号点减小。与跨中截面类似，3号点部位、即顶板悬臂端部的畸变效应受高跨比影响最为突出。

综合而言，对应于32 m标准跨度时的高跨比0.09，跨中截面的翘曲比例系数ξ总体上小于15%，而l/4截面的翘曲比例系数ξ接近于0，说明既有标准设计的高跨比设置对畸变效应不敏感，是非常合理的设计参数取值。

3.2截面参数对畸变翘曲比例系数ξ的影响

截面宽高比(b/h)、截面壁厚δ也是对截面畸变效应有较大影响的参数，在图1标准设计的基础上，进一步研究b/h和δ变化对翘曲比例系数的影响。研究中，选择畸变效应最大的1号点为研究对象。计算跨径分别取24，32和40 m；箱壁厚度δ主要考虑顶、底板平均厚度，分别取20，30和40 cm；其中宽高比通过保持底板b不变而高度h改变实现。不同跨度下，b/h和δ变化对跨中截面1号点的翘曲比例系数影响趋势如图8所示。

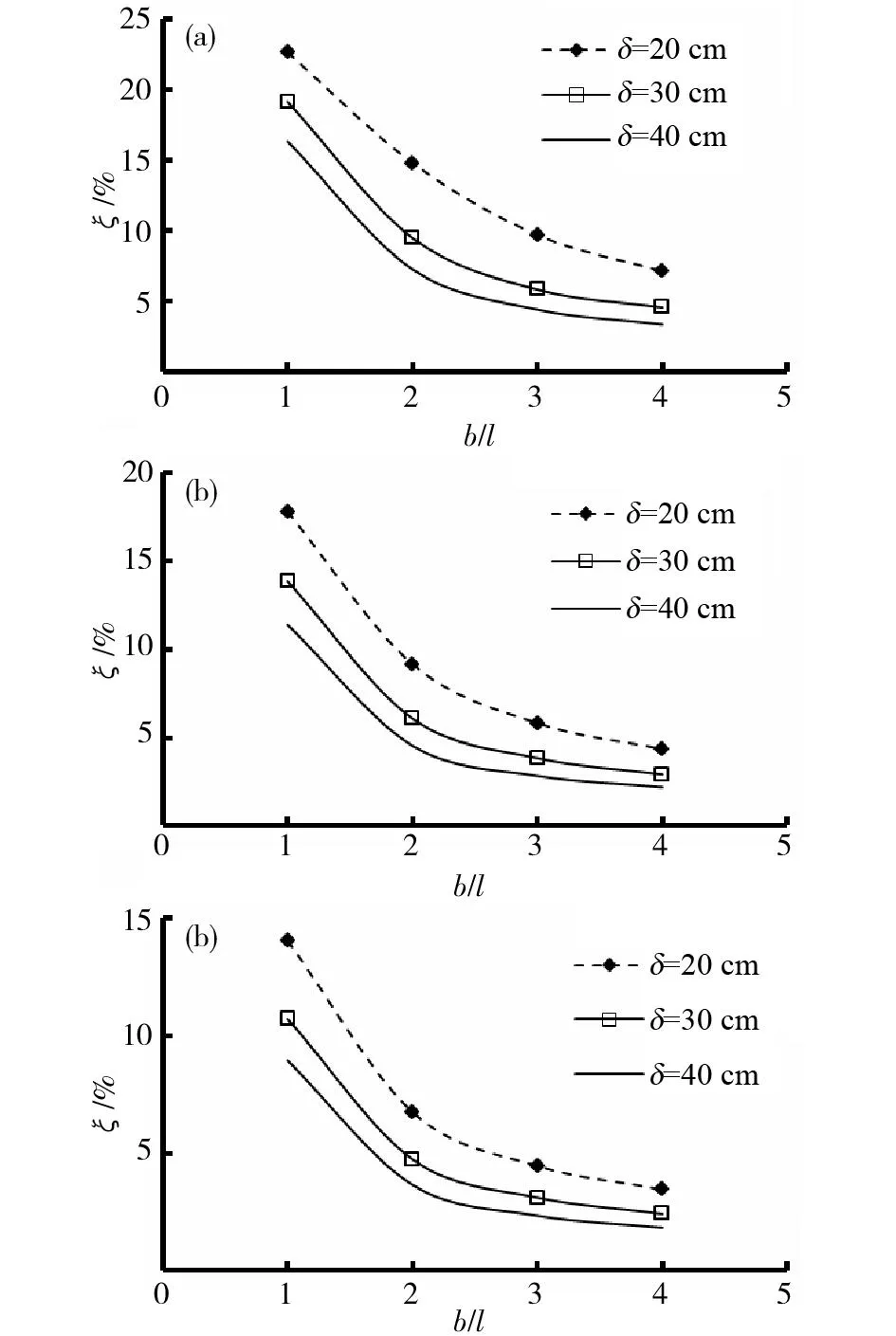
(a)计算跨径24 m；(b) 计算跨径32 m；(c)计算跨径40 m图8　截面参数对翘曲比例系数ξ的影响Fig.8 Effect of sectional parameters on distortion ratio

由图8可以看出，不同跨度下的翘曲比例系数对比表明，跨度越大畸变效应越小，这与3.1节规律一致。在箱梁跨径一定的情况下，翘曲比例系数ξ随宽高比增大而减小，说明截面高度越大、畸变效应越突出，截面底板宽度越小、畸变效应越突出。不同壁厚结果表明，壁厚越大翘曲比例系数越小，说明增大壁厚增加可抑制畸变效应。

4结论

1)双线铁路箱梁在仅单线活载最不利作用时，腹板与底板的交界部位、腹板与顶板的交界部位和顶板翼缘板悬臂端部为翘曲正应力较大部位，其中腹板与底板交界部位应力最大，设计ZK特种活载下的畸变产生的纵向正应力可达总纵向应力的14%。设计中应充分考虑畸变对桥梁受力的影响。

2)现有时速250 km/h铁路32 m跨度双线标准箱梁跨中和l/4截面的畸变效应分析表明，既有设计的截面参数对应的高跨比0.09是最优的高跨比，此时跨中最大翘曲比例系数小于15%，而l/4截面的翘曲比例系数ξ接近于0。

3)箱梁高跨比、宽高比、壁厚等设计参数对畸变效应均有一定影响，总体规律是高跨比越大，畸变效应越小；跨高比越大，畸变效应越小；壁厚越大，畸变效应越小。

参考文献：

[1] 郑健. 中国高速铁路桥梁[M]. 北京: 高等教育出版社, 2008.

ZHENG Jian. High-speed bridge engineering in China[M]. Beijing： Higher Education Press, 2008.

[2] 贾卫华. 武广高速铁路双线整孔简支箱梁预制技术[J]. 铁道科学与工程学报, 2010,17(2): 74-78.

JIA Weihua. Prefabricating technology of double line whole-span simply supported box girder in Wuguang high speed railway [J]. Journal of Railway Science and Engineering, 2010,17(2): 74-78.

[3] TB10002.3—2005,铁路桥涵钢筋混凝土和预应力混凝土结构设计规范[S].

TB10002.3—2005, Code for design on reinforced and prestressed concrete structure of railway bridge and culvert [S].

[4] 项海帆.高等桥梁结构理论[M]．2版.北京: 人民交通出版社, 2013．

XIANG Haifan．The higher bridge structure theory[M]．2nd edition. Beijing: China Communications Press，2013．

[5] 郭金琼，房贞政，郑振. 箱形梁设计理论[M]. 2版.北京:人民交通出版社, 2008.

GUO Jinqiong, FANG Zhenzhen, ZENG Zhen.Design theory of box girder[M]. 2nd edition.Beijing:China Communications Press, 2008.

[6] Jonsson J. Distortional theory of thin-walled beams [J]. Thin-Walled Structures, 1999,33(4): 269-303.

[7] 张士铎, 刘吉柱. 单室薄壁梯形箱梁的畸变应力[J]. 北京工业大学学报, 1987,13(1): 79-92.

ZHANG Shiduo, LIU Jizhu. Distortion stress in a trapezoidal box girder with single-cell [J]. Journal of Beijing Uuniversity of Technology, 1987, 13(1): 79-92.

[8] 徐勋, 强士中. 薄壁箱梁畸变分析理论的研究[J]. 工程力学, 2013, 30(11): 192-201.

XU Xun, QIANG Shizhong.Researchon distortion ananlysis theory of thin-walled box girder[J]. Engineering Mechanics, 2013, 30(11): 192-201.

[9] Ghani Razaqpur A, Li Hangang. Thin-walled multicell box-girder finite element[J].Journal of Structural Engineering,1991, 117(10):2953-2971.

[10] 张莉. 横隔板及几何特征对钢箱梁畸变效应的影响[J]. 铁道工程学报，2013, 29(8)：68-73.

ZHANG Li. Influences of diaphragm plate and geometric characteristics on distortion effect of steel box girder[J].Journal of Railway Engineering Society, 2013, 29(8):68-73.

[11] TB 10020—2009, 高速铁路设计规范(试行)[S].

TB 10020—2009, Code for design of high speed railway[S].

Distortion effect of double track railway box girders with speed of 250 km/h

LIN Pengzhen,SUN Lixiang，JI Wei , YANG Zijiang

(Key Laboratory of Road Bridge and Underground Engineering Gansu Province, Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract:In order to calculate the distortion effect of double track railway box girders at the speed of 250 km/h, a numerical model is established based on shell finite element method. Using finite element method and the traditional analytical method, distortion stress is calculated and analyzed under only single track live load. By defining the parameters of warping ratio, the rules of warping stress influenced by the design parameters of high span ratio, width span ratio and wall thickness are analyzed. Comparing with the traditional analytical solution, the finite element method is more suitable for the analysis in the box girder distortion effect. Under eccentric live load of single track, the value of warping ratio on flange edge of top plate is 11.6%, while it is 13.9% near the intersection of the web and the bottom plate which is the maximum in mid-span section. Analyzing the warping ratio on sections of mid-span and l/4, it is shown that the beam design parameters of existing box is reasonable. The maximum warping ratio on mid-span section is less than 15%, while nearly 0 on l/4 section. The design parameters of high span ratio, width span ratio and wall thickness can influence the sectional distortion of box girder. It is found that the distortion effect decreases with the increase of the high span ratio, width span ratio and wall thickness.

Key words：railway box girder；distortion；warping stress；numerical analysis

中图分类号：U441+.5

文献标志码：A

文章编号：1672-7029(2016)04-0595-05

通讯作者：蔺鹏臻(1977-)，男，甘肃甘谷人，甘肃省“飞天学者”特聘教授，博士，从事桥梁结构设计理论的研究；E-mail：pzhlin@mail.lzjtu.cn

基金项目：国家自然科学基金资助项目(51368031);甘肃省基础研究创新群体项目资助(1506RJIA029)

收稿日期：2015-09-08