轴重30 t重载列车作用下新黄土区隧道适应性及强化措施研究

刘聪，彭立敏，雷明锋，施成华

(中南大学 土木工程学院，湖南 长沙 410075)



轴重30 t重载列车作用下新黄土区隧道适应性及强化措施研究

刘聪，彭立敏，雷明锋，施成华

(中南大学 土木工程学院，湖南 长沙 410075)

摘要:以在建的蒙华铁路典型隧道结构型式为基础，针对新黄土区重载铁路隧道结构动力响应、疲劳寿命以及合理强化措施等问题，采用数值模拟的方法进行研究。结果表明：随着轴重和运量的增加，既有铁路隧道无法满足30 t轴重列车长期安全运营的要求，应采取强化措施。而单一的系统锚杆注浆加固强化能力有限，须采用系统锚杆与隧底地基加固(加固深度4 m及其以上)的联合强化措施方能满足其疲劳寿命要求。通过研究，指出30 t轴重列车荷载作用下隧底结构疲劳易损位置，即二次衬砌仰拱中心、初期支护仰拱与边墙连接处，并得到满足100 a设计使用年限，新黄土区隧道二次衬砌、初期支护混凝土结构在轴重30 t列车荷载作用下的疲劳上限强度，分别为1.30和1.62 MPa，可为设计参考。

关键词：30 t轴重；重载铁路隧道；适应性；疲劳寿命；强化措施

重载铁路以其高运量、低成本的优点，越来越受到世界各国铁路建设者的青睐。相比于普通铁路，重载列车的轴重更大，线下结构承受的动力冲击也更大，这无疑增加了基底病害的发生概率。在重载铁路隧道中，隧底结构在重载列车作用下更容易产生疲劳累积损伤，以致影响行车安全。据调查，我国重载铁路—大秦线自开通以来，随着轴重及运量的增加，多座隧道出现了不同程度的基底破损和翻浆冒泥等病害，且有逐年加重的趋势[1]。可见，既有铁路隧道对列车轴重增加的适应能力尚有待提升。也正因为如此，近年来，国内外众多学者对该问题开展了广泛研究。在病害调查分析方面，牛亚彬[1]对朔黄重载铁路77座隧道病害进行统计，并采用数值计算、现场试验等手段分析相关病害的形成机理和发展规律，给出了相应的处治对策。冯冀蒙等[2]对不同时期、不同地质条件下隧道的病害产生规律进行统计分析。在数值模拟研究方面，王秀英等[3]采用有限元方法分析得到轴重30 t列车荷载作用下隧道二次衬砌的动力响应特征。在现场动力实测方面，付兵先等[4]对朔黄重载铁路三家村隧道进行了现场测试，获得不同围岩区段填充层顶面处的动压应力幅值。在隧道结构长期服役性能研究方面，黄娟[5]从疲劳累积损伤的角度出发，研究引起铁路隧道结构产生疲劳损伤的主要原因，指出围岩条件对二次衬砌仰拱的动力响应和动力损伤影响较显著。Lei等[6]针对列车长期反复荷载作用下岩溶地基的累积沉降变形问题进行了分析，指出经处理后的岩溶区隧底结构累积变形值不会对列车长期运营安全造成破坏性影响。晏伟光[7]采用数值模拟方法分析不同轴重、不同设计参数对隧底疲劳寿命的影响。徐新利等[8-9]分别以朔黄重载铁路隧道工程为背景，研究轴重30 t列车荷载作用下基底吊空、欠密实病害对隧底结构受力的影响。诸如此类的研究还有很多[10]，相关研究成果也为我国重载铁路建设提供了有益参考。但纵观这些研究成果，尚没有见到新黄土区重载铁路隧道的相关成果报道，而我国在建及规划中的重载铁路就存在穿越大片黄土区域的情况，可以预见，未来几年中将有大量的黄土区重载铁路隧道需要修建。与常规软弱围岩相比，新黄土动力性能差，在长期反复重载作用下，更容易出现各种结构病害。因此，针对黄土区重载铁路隧道的动力特性和疲劳寿命问题开展相关研究具有重要的前瞻意义，可为我国即将或正在兴建的黄土区重载铁路隧道提供参考。

1动力计算模型

1.1典型黄土区重载铁路隧道结构型式

在建的蒙华重载铁路沿线经过大量黄土地区，相应的隧道工程具有代表性和典型性，故可作为研究对象。典型的黄土区隧道结构型式如图1。

1.2数值模型的建立

采用大型有限元软件建立隧道-围岩耦合三维计算模型。模型中模拟2节轴重30 t重载列车以72 km/h的速度通过长30 m的隧道，且考虑双线同时加载。模型范围水平方向以隧道左右侧外边缘向外延伸50 m，竖直方向自隧道底部向下取75 m，自隧道拱顶向上取至地表，地表埋深按浅埋考虑，埋深取15 m，如图2。

考虑不同地质年代、孔隙率和含水率等的黄土力学性能差异很大，本文研究中围岩仅取新黄土，且为服从Mohr-Coulomb屈服准则的弹塑性材料；初期支护、二次衬砌、填充层、底座板、弹性垫层、轨道板和钢轨等隧道结构均采用实体单元，仅按线弹性材料考虑。相关计算参数取值见表1。

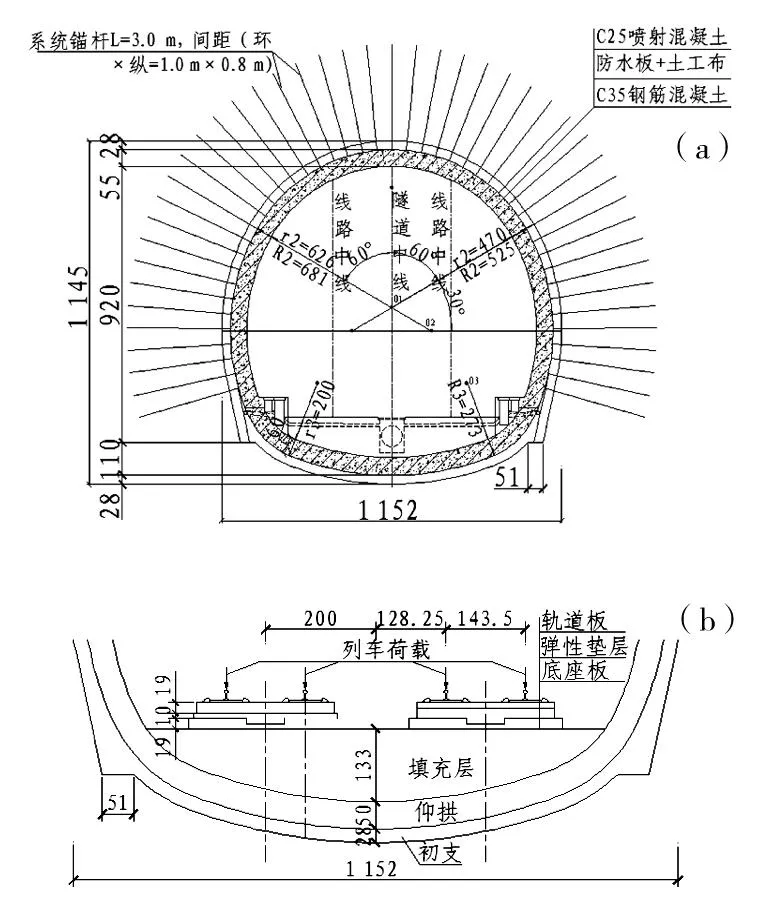
(a)横断面；(b)底部结构图1　蒙华重载铁路隧道结构设计图Fig.1 Tunnel supporting structure of Menghua heavy haul railway

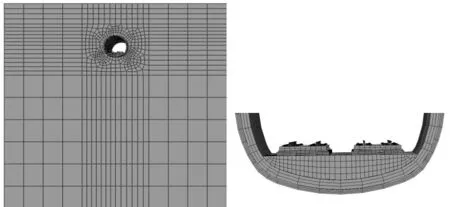
(a)整体模型 ；(b)底部结构图2　计算模型Fig.2 Calculation model

材料重度γ/(kN·m-3)弹性模量E/GPa泊松比μ抗拉强度ft/MPa抗压强度fc/MPa二衬(C35)2631.50.22.2023.4初支(C25)2528.50.21.7816.7填充(C25)2519.80.31.7816.7底座板(C30)25300.22.0120.1弹性层(C30)22200.22.0120.1轨道板(C45)2733.50.22.5129.6材料重度γ/(kN·m-3)弹性模量E/GPa泊松比μ黏聚力c/kPa内摩擦角φ/(°)V级新黄土19.20.180.365025锚杆注浆岩体19.20.360.3510027复合基底200.770.2913530.5

1.3重载列车荷载模拟

列车荷载作用于钢轨表面，考虑车速、轨道几何不平顺及车轮扁疤等因素导致的随机振动带来的附加作用力后，可近似用以下激励函数来模拟：

F(t)=P0+P1sin(ω1t)+P2sin(ω2t)+

P3sin(ω3t)

(1)

式中:P0为车辆静载；P1，P2和P3均为振动荷载；ωi为不平顺控制条件下的振动圆频率，对应的典型值可参见文献[11]。

列车为轴重30 t煤炭敞车，如图3。于是，可得到30 t轴重列车通过隧道时轨下反力时程曲线即列车荷载谱曲线，如图4。

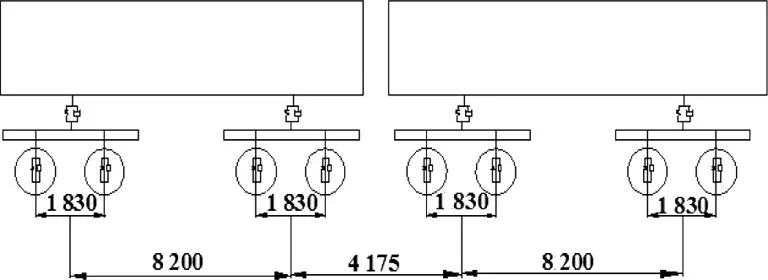
图3　30 t轴重车辆轴距图Fig.3 Wheelbase of 30 t axle train

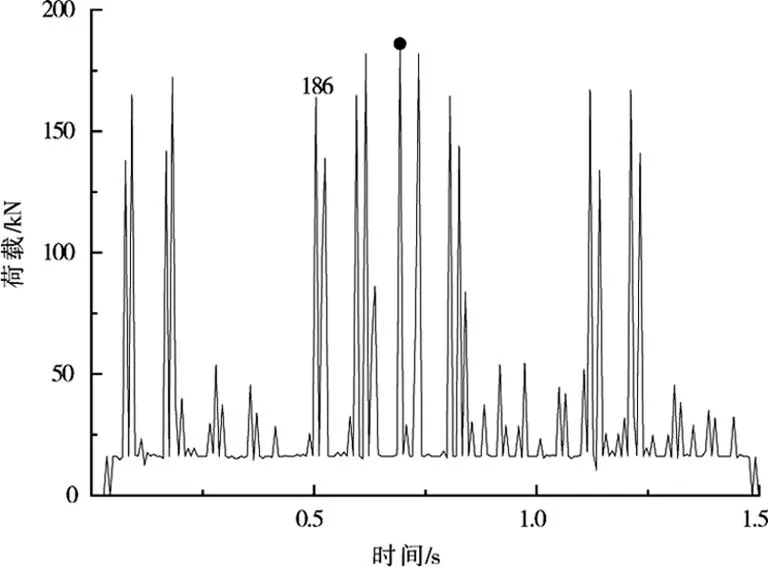
图4　30 t轴重列车荷载谱Fig.4 Load spectrum of 30t axle train

1.4混凝土疲劳寿命曲线

疲劳寿命曲线(即S-N曲线)是以试验数据为基础，统计某种等幅应力循环作用下直至结构产生疲劳破坏所能经受的最大循环次数，S代表材料或结构的应力水平，可以用最大应力水平Smax和最小应力水平Smin等来表示，如Smax=σmax/fc；N表示疲劳寿命，即疲劳失效时的循环加载次数，一般可用lgN来表示，典型的混凝土疲劳寿命曲线如图5所示。

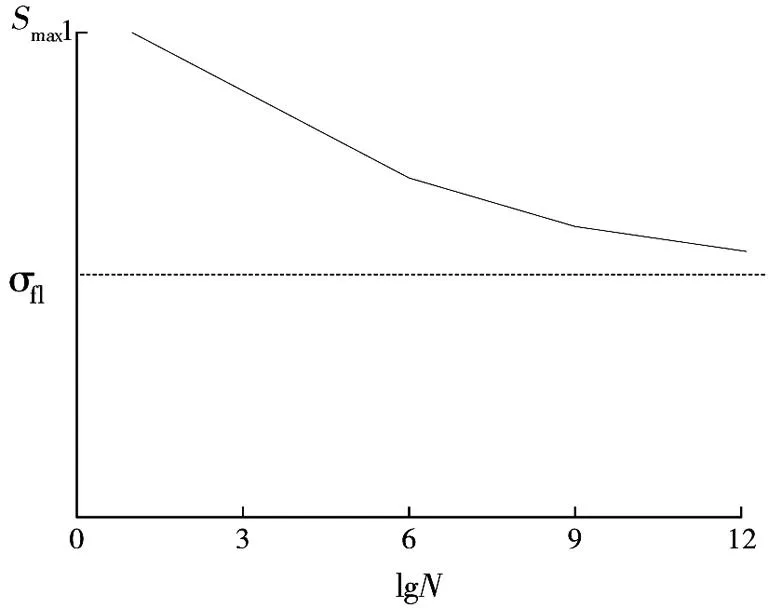
图5　疲劳寿命曲线(S-N曲线)Fig.5 Fatigue life curve (S-N curve)

我国混凝土结构设计规范对混凝土结构疲劳寿命仅作了定性要求[12]，而欧美等发达国家通过大量的混凝土疲劳试验，给出了相对成熟且详尽的疲劳寿命曲线[13]。对于处于纯拉状态下的素混凝土：当0≤St,min≤0.8时，在等应力幅度作用下的混凝土疲劳寿命(Ncf)通过式(2)确定；当St,min>0.8时，可采用St,min=0.8时的S-N曲线。

(2)

其中：

1) 若lgN1≤6，则lgNtf=lgN1；

2) 若lgN1>6，且ΔSc≥0.3-0.375St,min，则lgNtf=lgN2；

3) 若lgN1>6，且ΔSt≤0.3-0.375St,min，则lgNtf=lgN3。

式中：St,max为混凝土最大拉应力水平；St,min为混凝土最小拉应力水平；ΔSt为混凝土应力幅度。上述公式同样适用于计算拉-压或纯压状态下素混凝土的疲劳寿命[13]。

1.5疲劳累积损伤

计算得到结构的动力响应后，需要对其应力循环进行统计，并结合Miner累积损伤理论来对隧底结构的疲劳损伤情况。Miner线性疲劳累积损伤理论认为各应力循环作用所产生的损伤互不相关，每种应力循环所产生的疲劳损伤只与其循环次数有关，与加载顺序无关，各种不同应力循环产生的损伤可以线性叠加，当累积值超过某一定值时，结构将发生破坏，不同应力循环产生的累积损伤值可按下式进行计算：

(3)

式中：D为疲劳累积损伤值；Ni为某一应力水平下产生疲劳破坏的循环次数；ni为结构经受该应力水平的循环次数。

以蒙华铁路远期设计为例，该线路每列列车运量为2万t，年运量2亿t，设计使用年限为100 a，总的运量为200亿t，则隧道在设计使用年限内将1×106列列车通过，可得到隧道100 a内经受的总应力循环次数。当隧道在100 a内经受的总的应力循环所产生的疲劳累积损伤值不大于1时，则能适应重载列车在设计使用期内的安全运营。

2隧底结构动力响应分析

2.1仅考虑列车动载的隧底结构动力响应

尽管市场不断扩大、业务不断增长，IoT仍处于技术发展的初期，依旧面临一系列的安全隐患，庞大的数量和自身的脆弱性使得IoT设备极易成为黑客的首选目标。电影《速度与激情8》中数以万计的智能车辆被“天眼”系统恶意操控，进而组成“僵尸车联网”围剿国防部长；再如，2016年下半年，Mirai病毒控制超过30多万台的IoT设备对Dyn公司、OVH公司发动大规模分布式拒绝服务（DDoS）攻击，致使164个国家或地区受到影响。因此，IoT产业化的日益加速与技术的安全可信之间的矛盾成为该领域急需解决的重要问题，也是推动新型IoT技术发展的重要因素之一。

图6～7为仅考虑列车动载作用下隧底结构的动力响应时程曲线。从中分析可见，转向架通过时隧底引起的结构动应力最大，单个轮对通过时次之。列车转向架两相邻轮对通过时，会产生4个应力峰值，单个轮对通过时产生2个应力峰值。

进一步提取轨下断面填充顶部点A1，二次衬砌仰拱顶部点A2，初期支护仰拱顶部点A3以及隧底围岩处点A4的动力响应数据，具体点位选取如图8，得到隧底结构动应力沿轨下深度变化规律，如图9。

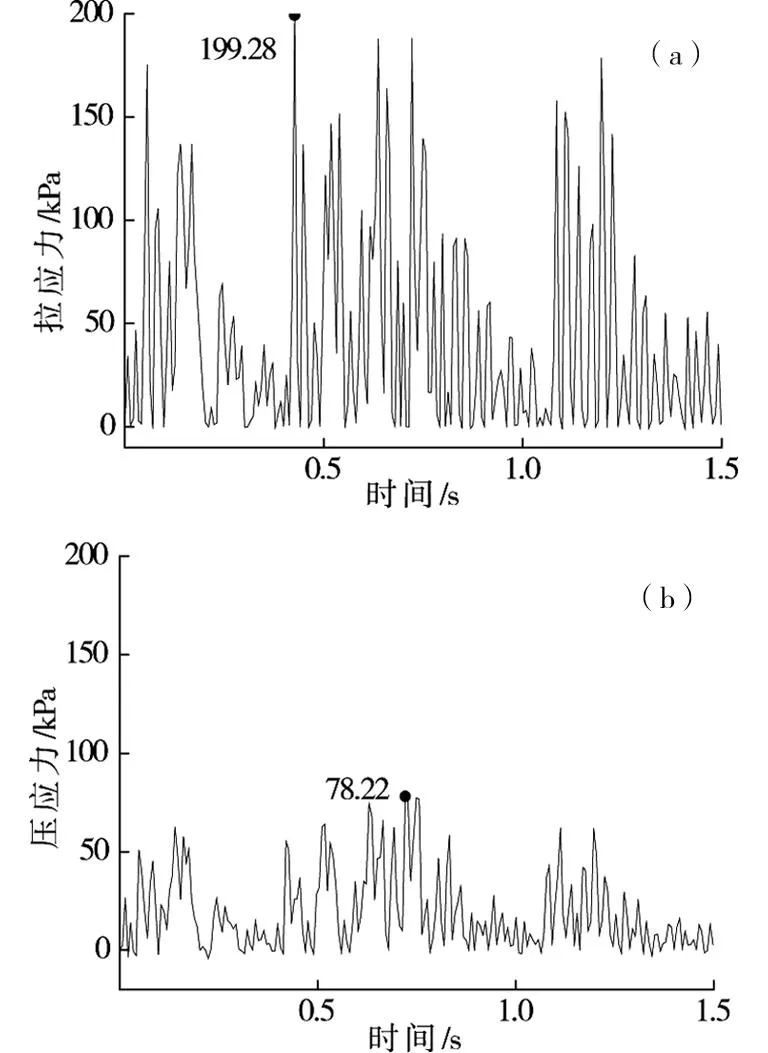
(a)拉应力；(b)压应力图6　隧道轨下二衬顶面应力时程曲线Fig.6 Dynamic stress time-history curves of secondary lining under the rail

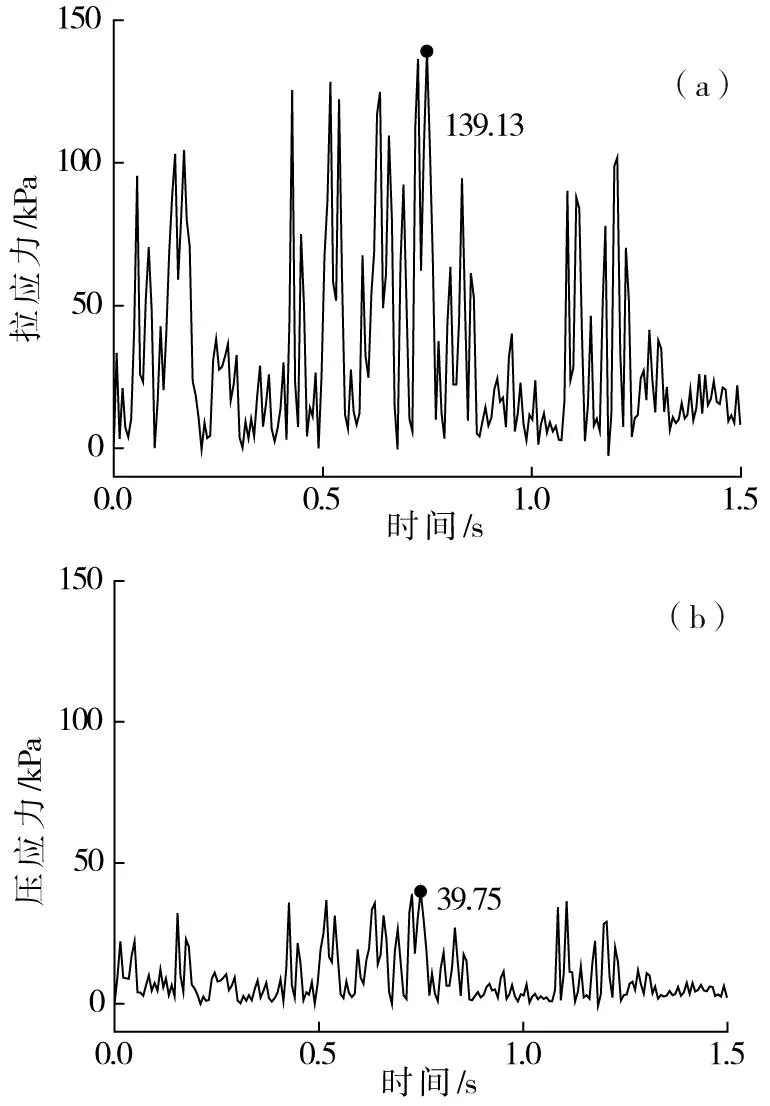
(a)拉应力；(b)压应力图7　隧道轨下初支顶面应力时程曲线Fig.7 Dynamic stress time-history curves of initial support

从中分析可知：1)动拉应力随深度先增加后减小，在二次衬砌仰拱中达到峰值199.28 kPa，初期支护中拉应力次之，初期支护与土的交界面处衰减为二次衬砌仰拱隧中最大动拉应力的3.35%。2)压应力随深度呈线性减小，填充层顶面最大压应力为133.5 kPa，而初期支护与土体交界面处迅速衰减为填充顶最大动压应力的8.91%。

图8　轨下断面点位Fig.8 Points under the rail

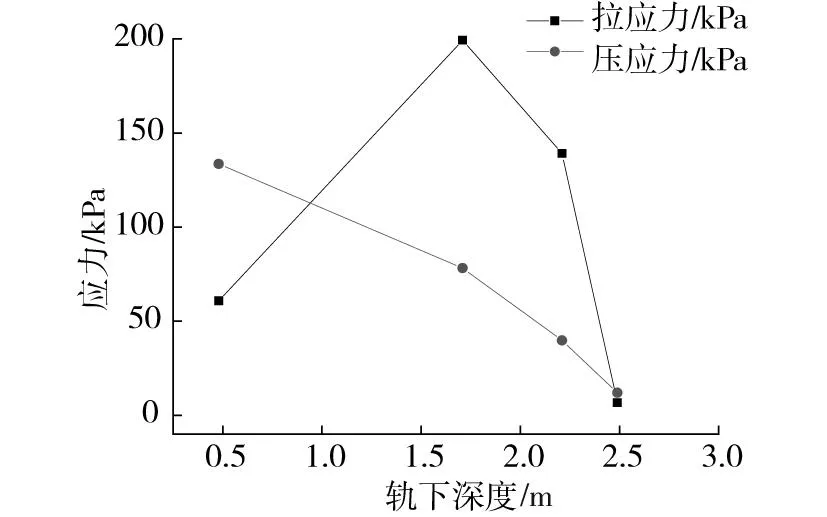
图9　隧底动应力沿轨下深度传递规律Fig.9 Dynamic stress transmission mechanism of bottom structures under the rail

2.2考虑动静荷载耦合作用的隧底结构动力响应

隧道开挖后，围岩压力静载作用将使隧道衬砌结构产生应力及变形，与列车荷载作用下的动力响应相互耦合，隧道结构在两者耦合作用下的应力云图如图10～11。

(a) 拉应力;(b) 压应力图10　动静荷载耦合作用下新黄土隧道二衬应力云图Fig.10 Coupled stress contour of secondary lining after loess tunnel excavation

(a) 拉应力;(b) 压应力图11　动静荷载耦合作用下新黄土隧道初支应力云图Fig.11 Coupled stress contour of initial support after

结果分析表明：1)相比于重载列车作用对结构产生的应力，围岩应力释放对结构所产生的应力贡献更大。2)二次衬砌与初期支护的最不利位置为仰拱与边墙连接处及仰拱中心位置，二次衬砌仰拱中心及初期支护连接处两部位的拉应力较大，二次衬砌仰拱与边墙连接处及初期支护仰拱中心分别为两者的压应力最大位置。

综合上述分析可见，二次衬砌仰拱中心及初期支护边墙与仰拱连接处两者的拉应力水平较大(图13)，为隧道结构的疲劳关键位置，二次衬砌及初期支护的压应力水平相较于其抗压强度小，远小于0.5ft，非结构疲劳破坏控制因素，压应力水平不会产生疲劳问题。

3隧底结构疲劳寿命及疲劳极限

强度

由上述分析可知，列车转向架通过时引起的应力最大，而隧道疲劳寿命主要是受大幅值应力循环的影响，小的应力波动无规律且对疲劳寿命影响很小，可以忽略，因此，可将列车转向架通过时的应力时程曲线简化为3种主要的应力循环，采用雨流计数原理对其进行统计，应力循环统计简化如图14。从中可得，每个转向架通过，即每节车厢通过时，最大应力循环为1个(1-2-7)，列车车轮通过时达最大拉应力，静力状态下为最小拉应力值。次级应力循环1个(4-5-6)，为每个轮对通过时引起的应力循环。低应力循环为2个(2-3-4)，为同一轮对两相邻车轮通过时引起的应力循环。

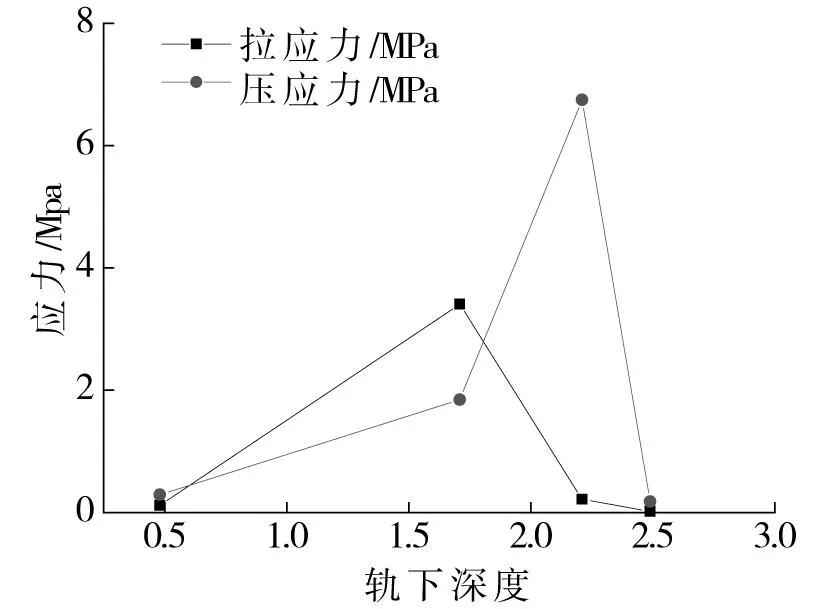
图12　隧底耦合应力沿轨下深度变化曲线Fig.12 Coupled stress of bottom structures under the rail

(a)二衬隧底中心;(b)初支连接处图13　隧底结构最大拉应力时程曲线Fig.13 Maximum tensile stress time-history curves of bottom structures in tunnel

轴重30 t煤炭重载敞车每节车厢载重97 t，每列206节车厢，于是可统计得到一列2万t列车通过时将产生1次大应力循环，207次中应力循环和412次低应力循环。

图14　应力循环简化图形Fig.14 Simplify counting figue of stress cycle

由此，可根据动力响应结果及疲劳寿命计算理论得到St,max和ΔSt等参数，代入S-N曲线公式可分别计算各处应力水平达到疲劳破坏时的应力循环次数Ni，如表2。同样已知容许的应力循环次数，也可求出相应的疲劳上限强度σfu，即初期支护C25喷射混凝土、二次衬砌仰拱C35混凝土对应的受拉疲劳上限强度分别为1.30和1.62 MPa。

表2　疲劳破坏时的应力循环次数

而根据第3节的计算结果，二次衬砌仰拱中心处拉应力最大为3.56 MPa，初期支护仰拱与边墙连接处最大拉应力为2.02 MPa，均超过抗拉疲劳上限强度，无法满足长期运营要求，须采取加固措施。

4重载铁路隧道适应性强化

当前关于隧底强化措施主要有系统锚杆注浆和地基处理(土挤密桩、灰土挤密桩)。本文对上述2种措施分别建立数值模型，探讨经强化处理后的隧道结构动力响应及疲劳寿命情况，以评价对应强化措施的有效性。

系统锚杆注浆加固后土体参数参照文献[14-15]选取。地基处理(土挤密桩加固)后的地层参数可按E=mEp+(1-m)Es计算[16]，式中，E为复合地基弹性模量；Ep为挤密桩弹性模量；Es为土体弹性模量;m为置换率。强化后的数值计算模型如图15。

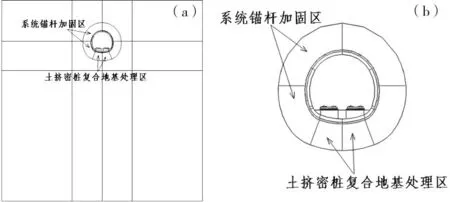
(a) 整体加固模型;(b) 加固处理区图15　加固模型Fig.15 Strengthening model

4.1单一系统锚杆强化后的计算结果分析

图16～17分别为系统锚杆加固长度取3及5 m时，二次衬砌仰拱中心及初期支护仰拱与边墙连接处等疲劳关键部位的应力时程曲线。从中分析可见：

1)隧底结构疲劳关键部位的应力峰值数据较无强化措施时有较大程度的减小，锚杆加固长度分别为3和5 m时，二次衬砌仰拱中心最大拉应力值比无强化措施时减小20.6%和28.5%，初期支护仰拱与边墙连接处分别减小32.5%和36.9%。2)强化后，相应部位最大拉应力值统计于表3，系统锚杆长度为3 m时，应力减小为1.36 MPa，仍大于受拉疲劳上限强度；而长度达5 m时，初期支护最大拉应力减小为1.27 MPa，小于疲劳上限强度，二次衬砌仰拱中心部位的最大拉应力仍有2.54 MPa，无法满足二次衬砌疲劳寿命要求，可见采用单一系统锚杆注浆对隧底结构应力水平减小有限。

表3系统锚杆注浆后隧底结构拉应力最大值

Table 3Maximum tensile stress of bottom structures after system anchoring bolt grouting

MPa

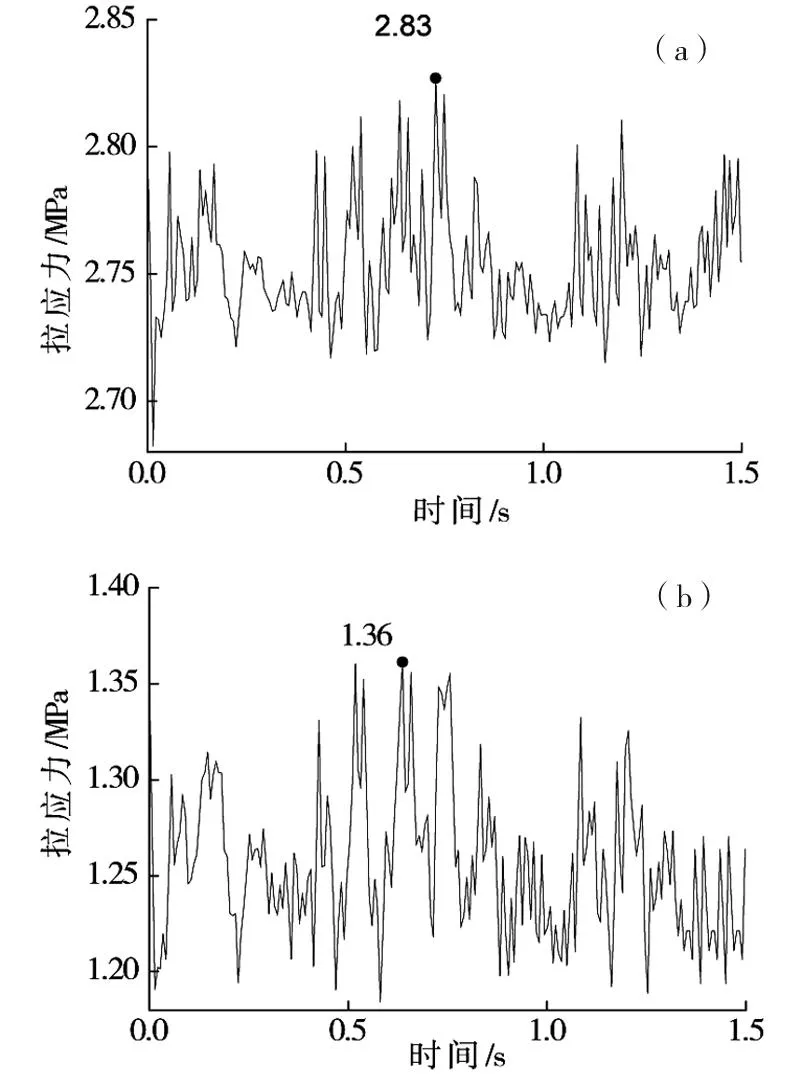
(a) 二衬仰拱隧中；(b) 初支连接处图16　锚杆注浆3 m时隧底结构应力时程曲线Fig.16 Stress time-history curves of buttom structures when the length of system anchoring bolt is 3 m

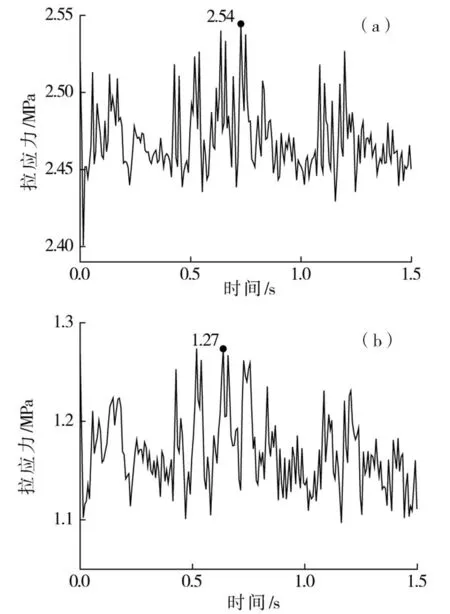
(a)二衬仰拱隧中；(b)初支连接处图17　锚杆注浆5 m时隧底结构应力时程曲线Fig.17 Stress time-history curves of buttom structures when the length of system anchoring bolt is 5 m

4.2系统锚杆和地基处理联合强化后计算结果

分析

以系统锚杆加固长度3 m为基础，地基处理深度分别取3和4 m，得到二次衬砌仰拱中心及初期支护仰拱与边墙连接处等疲劳关键部位的应力时程曲线如图18～19。

从中分析可知：1)经复合强化处理后，隧底结构疲劳关键部位的应力峰值数据较不加固时有显著的降低，基底加固深度分别为3和4 m时，二次衬砌仰拱中心最大拉应力值比不加固时减小49.1%和56.4%，初期支护仰拱与边墙连接处分别减小59.8%和61.2%。2)进一步提取隧底结构的最大拉应力值如表4，从中可见，系统锚杆注浆加固同时采用基底处理区域长度为4 m时二次衬砌仰拱中心、初期支护仰拱与边墙连接处应力水平均小于受拉疲劳上限强度，此时在轴重30 t重载列车作用下，黄土隧道结构能满足100 a设计寿命期内服役性能的要求。

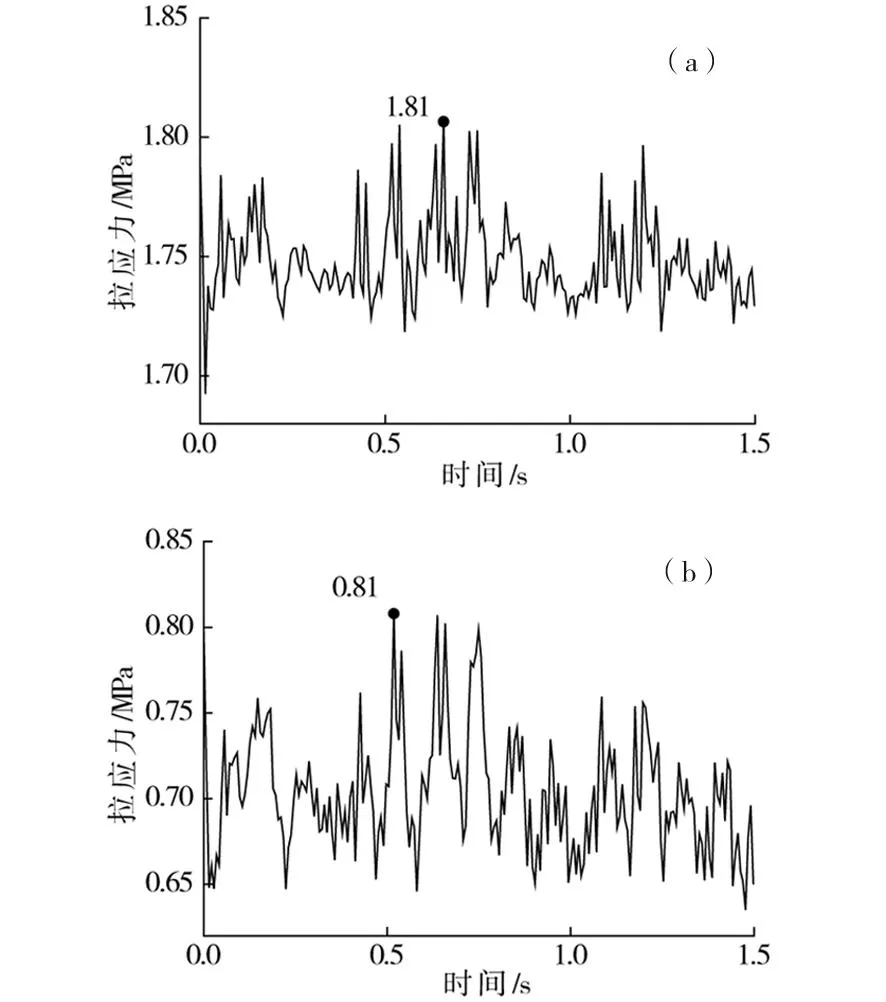
(a)二衬仰拱隧中;(b)初支连接处图18　锚杆注浆与地基处理半径为3 m时隧底结构拉应力时程曲线Fig.18 Stress time-history curves of bottom structures when the length of system anchoring bolt combined with ground treatment is 3 m

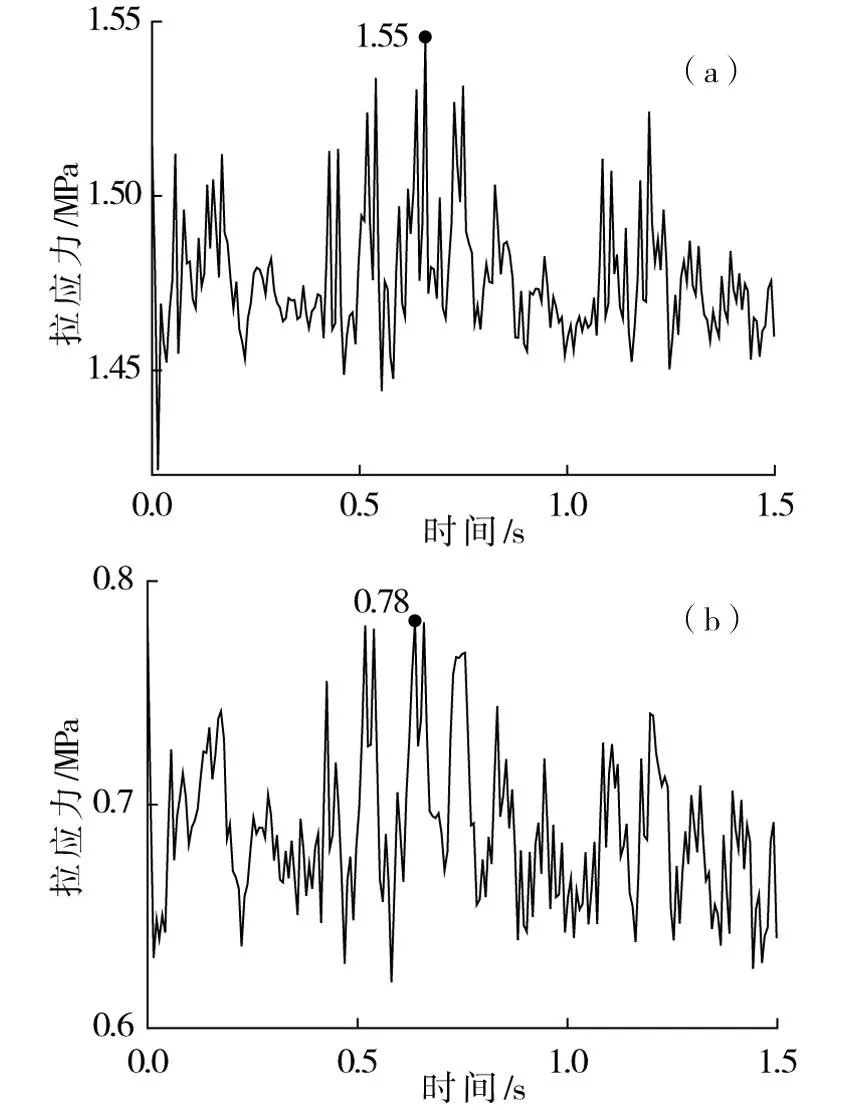
(a)二衬仰拱隧中;(b)初支连接处图19　锚杆注浆与地基处理半径为4 m时隧底结构拉应力时程曲线Fig.19 Stress time-history curves of bottom structures when the length of system anchoring bolt combined with ground treatment is 4 m

Table 4 Maximum tensile stress of bottom structures after ground treatment

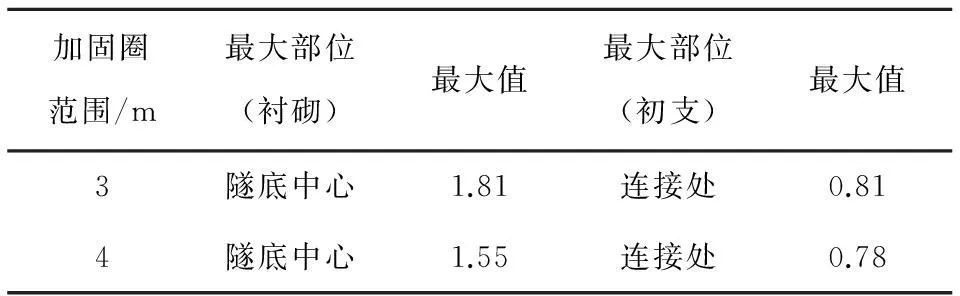
MPa

5结论

1)轴重30 t重载列车作用下，隧底结构动拉应力随深度先增大后减小，在二次衬砌仰拱中达到峰值，初期支护中拉应力次之，随后迅速衰减；动压应力在填充层顶面最大并随深度呈线性减小。

2)围岩应力与列车荷载耦合作用下，隧底结构拉压应力均先随轨下深度先增大后减小；隧底结构拉应力在二次衬砌仰拱中达到最大，压应力初期支护中达到最大，其中二次衬砌仰拱中心与初期支护仰拱与边墙连接处两者为疲劳损伤的最不利位置，且不能满足重载列车长期安全运营的要求。

3)根据重载铁路年运量、使用年限及疲劳寿命分析理论，可得新黄土隧道在30 t轴重荷载作用下，初期支护C25喷射混凝土、二次衬砌仰拱C35混凝土受拉疲劳上限强度分别为1.30和1.62 MPa。

4)单一的系统锚杆注浆加固对隧底结构应力水平降低的作用有限，锚杆长度达5 m时仍无法满足轴重30 t重载列车运行的适应性要求；而当采用系统锚杆加固和地基处理，基底应力水平的降低显著，处理深度达4 m时，可满足轴重30 t重载铁路新黄土隧道100 a设计运营期内服役性能的要求。

参考文献：

[1] 牛亚彬. 重载铁路隧道病害机理及整治技术研究[D]. 北京: 中国铁道科学研究院, 2013.

NIU Yabin. The heavy haul railway tunnel diseases mechanism and remediation technology research [D]. Beijing: China Academy of Railway Sciences, 2013.

[2] 冯冀蒙, 仇文革, 王玉锁, 等. 既有隧道病害分布规律及围岩环境等级划分研究[J]. 现代隧道技术,2013, 50(4): 35-41.

FENG Jimen, QIU Wenge, WANGYusuo, et al. Study of defect distribution regularity in existing tunnels and the classification of tunnel environments[J]. Modern Tunnelling Technology, 2013, 50(4): 35-41.

[3] 王秀英, 龚增进, 刘维宁. 30 t轴重条件下隧道技术标准研究[J]. 铁道工程学报, 2009, 128(5): 54-58.

WANG Xiuying, GONG Zengjin, LIU Weining. Research on the tunnel technical standard under 30t axis load [J]. Journal of Railway Engineering Society, 2009, 128(5): 54-58.

[4] 付兵先, 马伟斌. 重载列车作用下隧道基底荷载特征及动力学响应分析[J]. 铁道建筑技术, 2013(8): 1-5.

FU Bingxian, MA Weibin. Base load characteristics and dynamic response analysis of tunnel under heavy haul train[J]. Railway Construction Technology, 2013 (8): 1-5.[5] 黄娟. 基于损伤理论的高速铁路隧道结构振动响应分析及疲劳寿命研究[D]. 长沙: 中南大学, 2010.

HUANG Juan. Study on the vibration response and fatigue life of high- speed railway tunnels based on damage theory [D]. Changsha: Central South University, 2010.[6] LEI Mingfeng, OMER Joshua. Study on train vibration response and cumulative deformation of double arch tunnel in Kast foundation [J]. Geotechnical and Geological Engineering, 2015, 33(3): 549-558.

[7] 晏伟光. 重载铁路隧底结构动力响应及疲劳寿命研究[D]. 长沙: 中南大学, 2013.

YAN Weiguang. Research on dynamic response and fatigue life in bottom structure of heavy haul railway tunnel [D]. Changsha: Central South University, 2013.

[8] 徐新利. 30 t轴重重载列车作用下隧底脱空对基底结构受力的影响[J]. 铁道建筑，2015(4): 44-49.

XU Xinli. Influence of separation from tunnel's bottom on bearing capacity of base structure under train loading of 30 t axle load [J]. Railway Engineering, 2015 (4): 44-49.

[9] 薛继连. 30t轴重下隧底密实度对隧底结构受力的影响及隧底加固效果分析[J]. 中国铁道科学, 2015, 36(1): 90-95.

XUE Jilian. Analysis of the influence of tunnel bottom compactness on structure stress and strengthening measures under 30t axle load train [J]. China Railway Science, 2015, 36(1): 90-95.

[10] 丁祖德, 杜永刚, 彭立敏, 等. 基底围岩性状对高速铁路隧道结构动力响应的影响分析[J]. 现代隧道技术, 2015, 52(3): 88-94.

DING Zude, DU Yonggang, PENG Limin, et al. Influence of tunnel base rock mass properties on the dynamic response of high-speed railway tunnels[J]. Modern Tunnelling Technology, 2015, 52(3): 88-94.

[11] 梁波, 蔡英. 不平顺条件下铁路路基的动力分析[J]. 铁道学报, 1999, 21(2): 84-88.

LIANG Bo, CAI Ying. Dynamic analysis on subgrade of high speed railways in geometric irregular condition[J]. Journal of the China Railway Society, 1999, 21(2): 84-88.

[12] GB 50010—2010， 混凝土结构设计规范[S].

GB 50010—2010， Code for design of concrete structrues[S].

[13] CEB-FIP Model Code 2010, First Complete Draft [S]. Switzerland: Thomas Telford Services Ltd, 2010.

[14] 雷进生. 碎石土地基注浆加固力学行为研究[D]. 武汉: 中国地质大学, 2013.

LEI Jinsheng. Research on mechanical behavior of grout in gravelly soil foundations[D]. Wuhan: China University of Geosciences, 2013.

[15] 秦爱芳, 李永圃, 陈有亮. 上海地区基坑工程中的土体注浆加固研究[J]. 土木工程学报, 2000, 33(1): 69-72,82.

QIN Aifang, LI Yongpu, CHEN Youliang. Study on stabilizing grout of excavation pits in Shanghai district[J]. China Civil Engineering Journal, 2000, 33(1): 69-72,82.

[16] JGJ79—2012,建筑地基处理技术规范[S].

JGJ79—2012, Technical code for ground treatment of buildings[S].

Adaptability and strengthening research of 30 t axle heavy haul railway tunnel in new loess areaLIU Cong, PENG Limin, LEI Mingfeng, SHI Chenghua

(School of Civil Engineering, Central South University, Changsha 410075, China)

Abstract：Based on the typical tunnel structure of Menghua railway which is still under construction, a numerical study was performed, mainly focusing on the dynamic response, fatigue life and strengthening measures of loess heavy haul railway tunnel. The results show that: with an increase of axle load and railway freight transport volume, the existing railway tunnel cannot meet the long-term safety requirement without strengthening measures. The adaptability of loess heavy haul railway tunnel cannot be improved effectively by using sole systematic bolt, system anchoring bolt combined with ground treatment should be adopted (the length should reach to 4 m or more). Then the safety operation requirement of the heavy haul train can be satisfied. The research indicates that the centre of secondary lining of inverted arch, and sidewall and inverted arch joint of initial support are the most unfavorable load positions of the tunnel’s bottom structures under the action of 30 t axle heavy haul train. In order to satisfy the 100 a safety design service life of tunnel structures under the operation of 30 t axle heavy haul train, the upper-limit fatigue strength of initial and secondary lining of new loess tunnel were deduced, which are 1.30 MPa and 1.62 MPa, respectively. The results can provide reference for present design of heavy haul tunnel structures.

Key words：30 t axle; heavy haul railway tunnel; adaptability; fatigue life; strengthening measurements

中图分类号：U 25

文献标志码：A

文章编号：1672-7029(2016)04-0730-10

通讯作者：雷明锋(1982-)，男，湖南祁东人，博士，讲师，从事隧道与地下工程方面的教学与科研工作；E-mail:124520238@qq.com

基金项目：国家自然科学基金资助项目(U1361204，51278494)；湖南省创新平台与科技人才项目(2015RS4006)

收稿日期：2016-02-02