比拟杆法分析研究单箱三室箱梁剪力滞效应

赵志峰，蔺鹏臻，方炜彬

(兰州交通大学 甘肃省道路桥梁与地下工程重点试验室，甘肃 兰州 730070)



比拟杆法分析研究单箱三室箱梁剪力滞效应

赵志峰，蔺鹏臻，方炜彬

(兰州交通大学 甘肃省道路桥梁与地下工程重点试验室，甘肃 兰州 730070)

摘要:基于比拟杆法，推导单箱三室箱梁的比拟杆面积计算公式和剪力滞效应计算的控制微分方程。针对算例，分别采用本文理论、有机玻璃模型试验和有限元法分析简支箱梁和连续箱梁在集中力和均布荷载作用下的剪力滞效应。研究结果表明：本文理论解与有机玻璃模型试验解和板壳有限元解吻合良好。对简支箱梁，中腹板部位的顶和底板正应力均大于边腹板处顶和底板正应力。对连续箱梁，跨中截面中腹板处的顶和底板正应力均大于边腹板处和底顶板正应力。但对满跨均布荷载下的支座截面，底板正应力在边腹板部位大于中腹板部位，应力相差最大约12.91%。在单箱三室箱梁设计中考虑各腹板部位顶和底板正应力的差异，并以此确定有效翼缘分析宽度是非常必要的。

关键词：单箱三室箱梁；比拟杆法；剪力滞效应

剪力滞后效应是指箱梁上下翼板由于剪切变形的影响，而使得翼板的纵向正应力沿横向分布不均匀的现象[1]。忽略剪力滞效应的影响，就会低估箱梁腹板和翼板交接处的挠度和应力，从而导致不安全。在20世纪六七十年代，欧洲以及大洋洲等国家相继发生了4起大跨径钢箱梁桥梁坍塌或破坏的重大事故，对事故桥梁设计及计算的研究分析表明:造成事故的直接原因是设计理论上的失误,其中重要一项就是对剪力滞效应末加考虑[2-4]。国内外对箱梁剪力滞的研究理论和分析方法颇多，比拟杆法是其中一种。比拟杆法最早应用于航空结构力学当中。最初是1977年Taherian等将比拟杆法应用于研究不同截面类型的连续箱梁的剪力滞效应,提出了比拟杆应用在箱梁剪力滞效应研究当中的理论和分析方法[5]。在国内，1984年程翔云等[4]将比拟杆原理应用于计算单箱单室箱梁的剪力滞效应当中，提出了单箱单室箱梁剪力滞控制微分方程，并用样条函数逼近法求解了剪力滞效应。随着宽体箱梁在公路和铁路桥梁中的应用越来越广泛，剪力滞效应在宽体箱梁中更为突出[6]，所以建立一种简单而又精确的理论对宽体箱梁的剪力滞效应的分析研究很有必要。

1比拟杆法建立单箱三室箱梁的微分方程及求解

1.1比拟杆法的公式推导

1.1.1比拟杆模型

采用比拟杆法进行箱梁剪力滞效应分析时，通常将箱梁看做理想化的仅承受轴力的加劲杆与仅承受水平剪力的等效薄板的组合受力体系[4,7-8]。对于如图1(a)所示的单箱三室箱梁，其比拟杆模型截面如图1(b)所示。

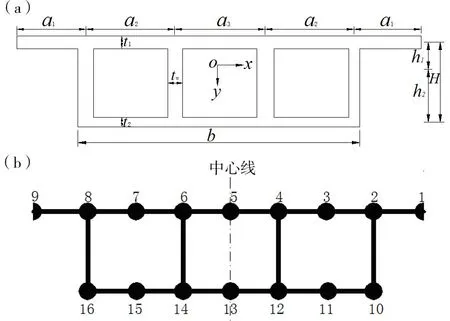
(a) 单箱三室箱梁截面；(b) 加劲杆与薄板等效体系图1　比拟杆法等效体系Fig.1 Equivalent system of the bar simulation method

1.1.2翼缘板等效面积和厚度公式推导

对于图1(a)所示的单箱三室截面箱梁,在竖向荷载作用下，按照初等梁理论计算上下翼缘板的弯曲应力为[4]：

(1)

(2)

式中:h1(2)为中性轴到上(下)翼板中面的距离；Aeu(b)为上、下翼板的等效翼板面积。

由于翼板为整个截面的惯性矩的贡献甚少，故忽略不计[7],因此按照图1(a)所示单箱三室箱梁截面的惯性矩为：

(3)

将式(3)代入式(2)中分别可以得出顶板和底板的等效翼缘板面积为:

(4)

Aeb=4α2Htw+3β2a2·t2

(5)

式(4)～(5)中：α1,β1和α2,β2分别为顶板和底板面积等效系数。

以箱梁顶板，底板的应力等效为原则[4,7],由式(2)可得：

(6)

则可得到顶、底板面积等效系数为：

(7)

(8)

(9)

(10)

故可得等效翼板厚度分别为：

teu=β1·t1

(11)

teb=β2·t2

(12)

1.1.3加劲杆面积公式

为了简化分析，可以将顶板采用9根加劲杆、底板采用7根加劲杆比拟，如图1(b)所示。按照比拟杆法原理[4,7-8]，理想化的加劲杆的面积等于实际加劲杆的面积再加上邻近薄板所提供的面积，可得顶板和底板的比拟杆面积公式如表1所示。

表1　比拟杆面积公式

1.2微分方程的推导

1.2.1比拟杆的平衡方程

当获得翼缘板面积等效系数和各加劲杆面积公式之后，可以杆为对象建立力学平衡方程。对于图2(a)所示一端固结、另一端自由的单箱三室箱梁(横截面对称取一半分析)，在距离约束端x截面处取ΔX微元，根据图2(b)所示薄板微段只受水平剪力和顶底翼板各加劲杆只受轴力的受力状态，可得到顶底板各加劲杆的静力平衡方程。

根据图2(c)可得顶板加劲杆平衡受力方程：

(13)

(14)

(15)

(16)

(17)

根据图2(d)可得底板加劲杆平衡受力方程：

(18)

(19)

(20)

(21)

(a) 单箱三室箱梁;(b) 薄板受力微段;(c) 顶板加劲杆平衡受力;(d)底板加劲杆平衡受力图2　悬臂箱梁翼板加劲杆及受力图示Fig.2 Force diagram of the three-cell cantilever box girder flange plate stiffeners

1.2.2顶、底板微分方程

对于图2(a)中，在箱邻两杆之间的微块上存在着剪切变形，其剪切角变化率以1和2杆之间为例，可表示为：

(22)

也可表示为：

(23)

由材料力学可知，剪力流表达式为：

q=rteuG

(24)

将式(24)两边求导后代入式(23)中，可得1和2杆之间受力方程：

(25)

对于其他各杆之间微块上建立受力方程的通用表达式为：

(26)

将式(26)两边一次微分可得：

(27)

对于图2(a)中的顶板和底板各加劲杆，将各杆的受力平衡方程代入式(27)，则可导出顶板、底板剪力滞效应控制微分方程组。

顶板剪力滞效应微分方程组：

(28)

(29)

(30)

(31)

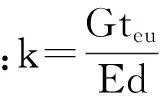
底板剪力滞效应微分方程：

(32)

(33)

(34)

qi(x)为 作用在i杆上的未知剪力流函数，i=1,2,3，…，n；qEi(x)为与腹板箱接处的加劲杆上的已知剪力流函数；E/G为截面抗弯，抗剪弹性模量；Ai为加劲杆面积；d为加劲杆杆间间距；σi/εi为第i根杆的正应力和正应变。

1.3边界条件

2)对于嵌固端则为：qi=0。

1.4单箱三室箱梁腹板中剪力流分配

直腹板多室薄壁箱梁在弯曲状态下，中腹板传递的剪力一般情况下大于边腹板传递的剪力，特别是在无悬臂的情况下更为明显[9]。因此，本文在求解已知剪力流的过程当中，根据文献[9]对受竖向荷载作用下的三室薄壁箱梁各腹板中所受的剪力进行了分配，进而求得已知剪力流，具体按照下面的公式进行。

(35)

由以上公式可以计算出已知剪力流qE1(X)和qE2(X)。

1.5微分方程组的求解

对于本文建立的顶板和腹板的剪力流微分方程组式(28)～(34)，可利用自编R程序[10-12](RStudio环境中运行)求解出各杆未知剪力流数值解，然后结合式(13)～(21)和式(35)，可以得到各加劲杆应力值。如顶板剪力滞控制微分方程组求解如下(算例)：

> fsub <- function (t,Y,pars) {

+ return(list(c(f1=Y[5],

+ f2=Y[6],

+ f3=Y[7],

+ f4=Y[8],

+ f5=233.265*Y[1]-66.466*Y[2]+242.819,

+f6=-66.466*Y[1]+148.626*Y[2]-82.159*Y[3]-242.819,

+f7=-82.159*Y[2]+149.727*Y[3]-67.082*Y[4]+346.278,

+ f8=-67.082*Y[3]+149.242*Y[4]-346.278)))

+ }

> x <- seq(0,1/2,len=100)

> print(system.time(

+ Soltwp <- bvptwp(x=x, func = fsub,

+yini=c(y1=NA,y2=NA,y3=NA,y4=NA,y5=0,y6=0,y7=0,y8=0),

+ yend=c(0,0,0,0,NA,NA,NA,NA))

+ ))

2算例及结果分析

2.1算例概况

为了验证本文提出的分析单箱三室箱梁剪力滞效应的比拟杆理论可靠性，采用有机玻璃制作跨度为1 000 mm的单箱三室简支箱梁模型和跨度为2 000 mm 的两跨连续箱梁模型(每跨1 000 mm)，材料的弹性模量E=2 600 MPa，泊松比=0.375，模型截面尺寸见图3(a)。分别对简支箱梁、连续箱梁(每跨)的跨中4块腹板对称作用660 N竖向集中荷载和沿梁长方向四块腹板上对称作用660 N/m均布荷载。本文中，只对简支箱梁承受集中荷载的工况做了试验，见图3(b)，其他荷载工况分别采用 Ansys有限元软件 Shell63 单元建立空间板壳有限元数值模型和本文理论解进行对比验证，有限元模型见图3(c)和3(d)。

(a)1/2模型截面；(b)加载图示；(c)简支梁有限元模型；(d)连续梁有限元模型单位：mm图3　截面及模型Fig.3 Section and model

2.2简支箱梁的剪力滞效应

以有机玻璃制作的单箱三室简支箱梁为例，根据式(28)～(34)，结合已知剪力流式(35)，可求得顶底板相邻加劲杆之间等效薄板中的未知剪力流数值，代入顶底板加劲杆受力平衡方程(13)～(21)中可得到加劲杆所承受的实际轴力，进而得到各加劲杆中的纵向正应力。

算例当中，对简支箱梁承受跨中集中荷载(此工况做了试验)和满跨均布荷载的情况进行计算，同时分别建立有限元模型进行数值对比，跨中截面应力对比见图4。

(a)集中力作用下跨中截面应力；(b)满跨均布荷载下跨中截面应力图4　简支梁跨中截面纵向应力Fig.4 Longitudinal stress of the simple box girder span middle section

由图4可以看出，本文理论解、板壳数值解以及试验解沿单箱三室箱梁横截面方向正应力分布的趋势一致，而且三者的结果吻合良好。表明本文理论解有较高的精度。本算例可以得出：对于单箱三室简支箱梁，当跨中承受对称集中荷载、满跨均布荷载时，跨中截面中腹板部位顶板处的正应力大于边腹板部位的顶板正应力，而且中腹板部位底板正应力大于边腹板部位底板正应力，腹板与翼板交界处的顶、底板应力都大于初等梁理论正应力，成正剪力滞效应。本算例表明多箱室简支箱梁在承受竖向荷载作用下，剪力在中腹板中分配较多，而在边腹板中分配较少。

2.3连续箱梁的剪力滞效应

为了进一步验证本文比拟杆理论解决单箱三室箱梁剪力滞效应的适用性。以图3(a)为截面的两跨连续箱梁为算例(每跨长1 m)，应用本文理论分别计算连续箱梁跨中4块腹板上承受对称集中力(660 N)和满跨4块腹板上承受均布荷载时跨中截面和支座截面的纵向正应力(计算方法如同简支梁计算)，同时与板壳数值解进行对比，以验证本理论在连续箱梁中的正确性。应力对比见图5。

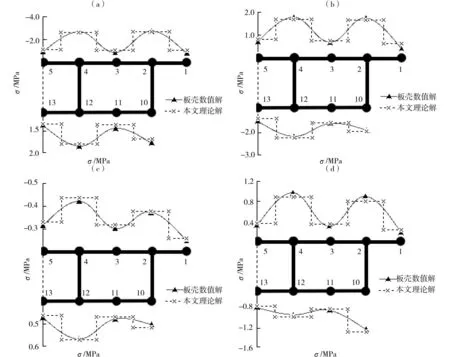
(a)集中力作用下跨中截面应力;(b)集中力作用下支座截面应力;(c)均布荷载作用下跨中截面应力;(d)均布荷载作用下支座截面应力图5　连续箱梁跨中截面、支座截面纵向应力Fig.5 Longitudinal stress of the continuous box girder span middle section and support section

由图5可以看出：本文理论解与板壳数值解的正应力分布趋势一致，而且二者的结果吻合良好，表明了本文建立的比拟杆方法对解决单箱三室连续箱梁剪力滞效应问题有较好的精度。从图5中可以得到：连续箱梁在集中荷载和满跨均布荷载作用下，跨中截面纵向正应力沿横截面的分布趋势和简支箱梁是大体相似的。但是对于满跨均布荷载作用下，支座截面边腹板部位底板正应力大于中腹板部位底板处正应力值(图5(d))，本算例中二者相差约12.91%。可见，剪力滞效应的影响之大在设计中是不容忽视的。

2.4精度分析

为了验证本文比拟杆法的精度，应用本文理论方法计算出了简支梁和连续梁承受荷载作用下关键截面的纵向正应力，与板壳有限元解和试验解进行了对比，结果见表2。

表2　简支梁、连续梁在不同荷载作用下主要截面应力值对比及误差

从表2中可以看出，本文理论计算出的应力值与有限元数值以及试验值结果基本逼近。连续梁承受集中荷载作用时，支座截面1号杆的应力值误差达到22%以外，其他误差都在10%以内。进一步验证了本文建立的比拟杆理论对于计算单箱三室箱梁剪力滞效用有良好的精度，可为工程设计配筋提供一定的参考。

3结论

1)通过与有机玻璃模型试验解、板壳数值解相比，本文比拟杆法的分析误差总体在10%以内，表明本文理论解在剪力滞基本规律和数值大小上均具有较好的精度。

2)对单箱三室简支箱梁，在跨中集中力和满跨均布荷载作用下，截面总体为正剪力滞效应。跨中截面上，各腹板部位顶、底板纵向应力有较大差异，顶板和底板的正应力在中腹板部位均大于边腹板部位。设计中考虑跨中截面各腹板部位顶、底板正应力的差异来确定有效翼缘分析宽度是非常必要的。

3)通过连续箱梁算例可以得到：在集中荷载和满跨均布荷载作用下，跨中截面各腹板处顶、底板纵向正应力沿横截面的分布趋势和简支箱梁跨中截面大体相似。但是对于满跨均布荷载作用下，支座截面边腹板部位底板正应力大于中腹板部位底板处正应力值，本算例中二者相差约12.91%。因此，在连续箱梁结构设计中考虑跨中截面和支座截面的顶、底板应力的差异是很有必要的。

参考文献：

[1] 郭金琼,房贞政,郑振.箱型梁设计理论[M].北京:人民交通出版社,2008.

GUO Jinqiong,FANG Zhenzheng,ZHENG Zhen.The design theory of the box girder[M].Beijing:China Communications Press,2008.

[2] 罗旗帜,吴幼明.薄壁箱梁剪力滞理论的评述和展望[J].佛山科学技术学院学报(自然科学版),2001,19(3):29-35.

LUO Qizhi WU,Youming.The review and prospect of thin-walled box girders shear lag theory[J].Journal of Foshan University(Natural Science Edition),2001, 19(3):29-35.

[3] 靳欣华,郑凯锋,陈艾荣.分析桥梁结构剪力滞效应的新方法[J].重庆交通学院学报,2002,21(4):4-8.

JIN Xinhua, ZHENG Kaifeng, CHEN Airong. The new method of the shear lag analysis in bridge structure[J].Journal of Chongqing Jiaotong University,2002, 21(4):4-8.

[4] 程翔云, 汤康恩.计算箱形梁桥剪力滞效应的比拟杆法[J]. 中南公路工程, 1984, 46(4):65-73.

CHENG Xiangyun,TANG Kangen, The bar simulation method to calculate shear lag effect of box girder bridge[J]. Central South Highway Engineering, 1984, 46(4):65-73.

[5] Taherian A R, Evans H R.The bar simulation method for the calculation of shear lag in multi-cell and continuous box girders[J]. Institution of Civil Engineers, Proceedings, 1977,63:881-897.

[6] 蔺鹏臻, 刘凤奎, 杨军, 等.箱梁剪滞翘曲位移函数的定义及其应用[J]. 计算力学学报, 2012,29(5):789-794.

LIN Pengzhen, LIU Fengkui ,YANG Jun, et al. The definition and application of shear lag wa-rping displacement function of box girder[J]. Chinese Journal of Computational Mechanics,2012,29(5):789-794.

[7] 邓德元, 陈清波, 李新平.比拟杆法在边箱形主梁剪力滞效应分析中应用研究[J].科学技术与工程, 2012, 12(26):6695-6700.

DENG Deyuan,CHEN Qingbo, LI Xinping. The researc-h and application of the bar simulation method in shear lag effect of the side box girders[J]. Science Technology a-nd Engineering,2012, 12(26):6695-6700.

[8] 贺栓海. 桥梁结构理论与计算方法[M]. 北京：人民交通出版社，2003.

HE Shuanhai.Theory and calculation method of bridge str-uctures[M].Beijing: China Communications Press,2003.

[9] 苏继红, 周军生, 陈炜.多室薄壁箱梁腹板剪力分配规律分析[C]// 中国公路学会桥梁和结构工程分会2004年全国桥梁学术会议论文集，2004.

SU Jihong, ZHOU Junsheng, CHEN WEI. The web shear distribution analysis of multichamber thin-walled box girder[C]// The 2004 National Bridge Conference Set of the Bridge and Structure Engineering Branch in China Highway Society, 2004.

[10] Karline S, Jeffre C, Francesca M. Solving differential equations in R[M]. Springer-Verlag Berlin and Heidelberg GmbH & Co. K, 2012.

[11] Cash J R, Mazzia F. A new mesh selection algorithm, b-ased on conditioning, for two-point boundary value codes[J].Comput Appl Math, 2005,184:362-381.

[12] Cash J R, Wright M H.A deferred correction method for n-onlinear two-point boundary value problems:implementation and numerical evaluation[J].SIAM J Sci Stat Comput, 1991,12: 971-989.

The bar simulation methodfor shear lag effect of three-cell box girdersZHAO Zhifeng，LIN Pengzhen，FANG Weibin

(Key Laboratory of Road Bridge and Underground Engineering Gansu Province , Lanzhou Jiaotong University, Lanzhou 730070, China)

Abstract:Based on the bar simulation method, the analogy bar area calculation formula and the control differential equation of shear lag effect for single box and three rooms girder were deduced . Taking the single box and three rooms girder for example, the shear lag effect was analyzed using the theoretical calculation with bar simulation method in this paper, model test research on simply supported box girder of organic glass and the numerical solution of plate and shell of simply supported box girder and continuous box girder under concentrated force and uniformly distributed load respectively. The results show that the theoretical calculation by bar simulation method in this paper is in good agreement with the other two methods mentioned above.The positive stress at roof and floor of mid-web is bigger than the stress at roof and floor of edge-web for simply supported box girder and the middle section of continuous box girder. But the positive stress at floor in the edge web site is bigger than the stress in mid-web site at the bearing section under uniform load. The greatest difference of stress is about 12.91%.Considering the difference of stress at roof and floor of each web in the bridge design, and the determination of the effective flange width analysis was very necessary.

Key words：the single box and three rooms girder；bar simulation method；shear lag effect

中图分类号：TU375.4

文献标志码：A

文章编号：1672-7029(2016)04-0697-08

通讯作者：蔺鹏臻(1977―)，男，教授，博士，甘肃天水人，从事大跨度桥梁结构的理论研究；E-mail:linpzh@126.com

基金项目：国家自然科学基金资助项目(51168030，51368031)；甘肃省基础研究创新群体资助项目(1506RJIA029)

收稿日期：2015-07-24