UHPC 三轴受压力学性能研究

周 俊，韦建刚，杨 艳，陈宝春，黄 颖

(1.福建船政交通职业学院土木工程学院，福州 350007；2.福州大学土木工程学院，福州 350108；3.福建工程学院土木工程学院，福州 350118)

建筑结构中的混凝土材料通常处于承受多轴应力状态[1-3]，而不是单轴应力状态。普通强度混凝土(NSC)和高强度混凝土(HSC)作为典型的结构材料，在工程结构中得到了广泛的应用。许多研究者对NSC 和HSC 在三轴压缩下的行为进行了研究。过镇海等[4]、宋玉普等[5]、丁发兴等[6]、KUPFER等[7]、WANG 等[8]、SFER 等[9]、SIRIJAROONCHAI等[10]和CHERN 等[11]以围压为试验参数，研究了不同围压强度对NSC 三轴强度的影响，以及NSC在多轴应力状态下的力学行为和破坏特征。自20 世纪90 年代以来，随着高强混凝土应用的日益广泛，LU 和HSU[12]、HE 和SONG[13]、周甲佳等[14]、LI 和ANSARI[15-16]和王怀亮[17]对不同强度等级的HSC 进行了围压约束下的三轴受力特性研究，得到HSC 在三轴压缩下的应力-应变曲线、强度变化规律和破坏模式等。

上述的研究对象主要是抗压强度小于120 MPa的NSC 和HSC。随着生产技术和材料科学的发展，单轴抗压强度不低于120 MPa 的超高性能混凝土(UHPC)应用越来越多[18]，然而，UHPC的多轴本构关系试验研究目前还较少。XU 等[19]对UHPC 的三轴压缩性能进行了试验研究，拟合得到UHPC 强度参数。WANG 等[20]对UHPC 在0 MPa～50 MPa 围压范围内进行单轴和三轴压缩试验，分析了UHPC在不同应力状态下的力学行为，并对基于Ottosen准则的UHPC 破坏面进行了修正。REN 等[21]对围压为0 MPa～100 MPa 下的单轴抗压强度为95 MPa和129 MPa 的φ50 mm×100 mm 圆柱形UHPC 试件进行三轴压缩试验，得到不同围压UHPC 应力-应变曲线，探讨UHPC 三轴压缩破坏准则和韧性，并确定Holmquist-Johnson-Cook 本构关系主要强度参数。VOGEL 等[22]试验研究了在围压为10 MPa、20 MPa 和30 MPa 下尺寸为φ100 mm×200 mm 的圆柱体UHPC 以及在15 MPa、30 MPa、60 MPa和90 MPa 的侧向应力下尺寸为100 mm×100 mm×100 mm 的立方体UHPC 的三轴抗压强度。余自若等[23]和吴礼程等[24]以围压和钢纤维掺量为试验参数，对UHPC 进行常规三轴试验，得到不同参数下的UHPC 应力-应变曲线。

由于UHPC 具有优良的经济性和环保性，可以预见这种材料在土木工程领域将得到越来越广泛的应用，开展UHPC 在多轴应力状态下的力学性能研究，具有重要的意义[25-26]。因此，本文以围压和钢纤维掺量为参数，开展UHPC 三轴受压力学试验，研究其破坏形态、应力-应变曲线、峰值应力和应变等力学性能，并对UHPC 八面体应力-应变关系和破坏准则进行了分析。

1 试验概况

1.1 试件设计

以围压大小和钢纤维掺量为参数，对UHPC进行常规三轴压缩试验研究，获得不同参数下的应力-应变全曲线，分析围压大小和钢纤维掺量对UHPC 试件应力-应变全曲线、峰值应力和应变的影响。试验参数如表1 所示，采用直径D为50 mm，高度H为100 mm 的UHPC 圆柱体试件，围压大小σ3取值为0 MPa、10 MPa、20 MPa、30 MPa 和40 MPa，钢纤维掺量φf为0%、1%、2%和3%。每组试件都分别制作三个，并取三个试件的平均结果进行分析，具体编号以U0-10 为例进行说明：U 表示UHPC；0 代表钢纤维掺量为0%；10 表示围压值为10 MPa。

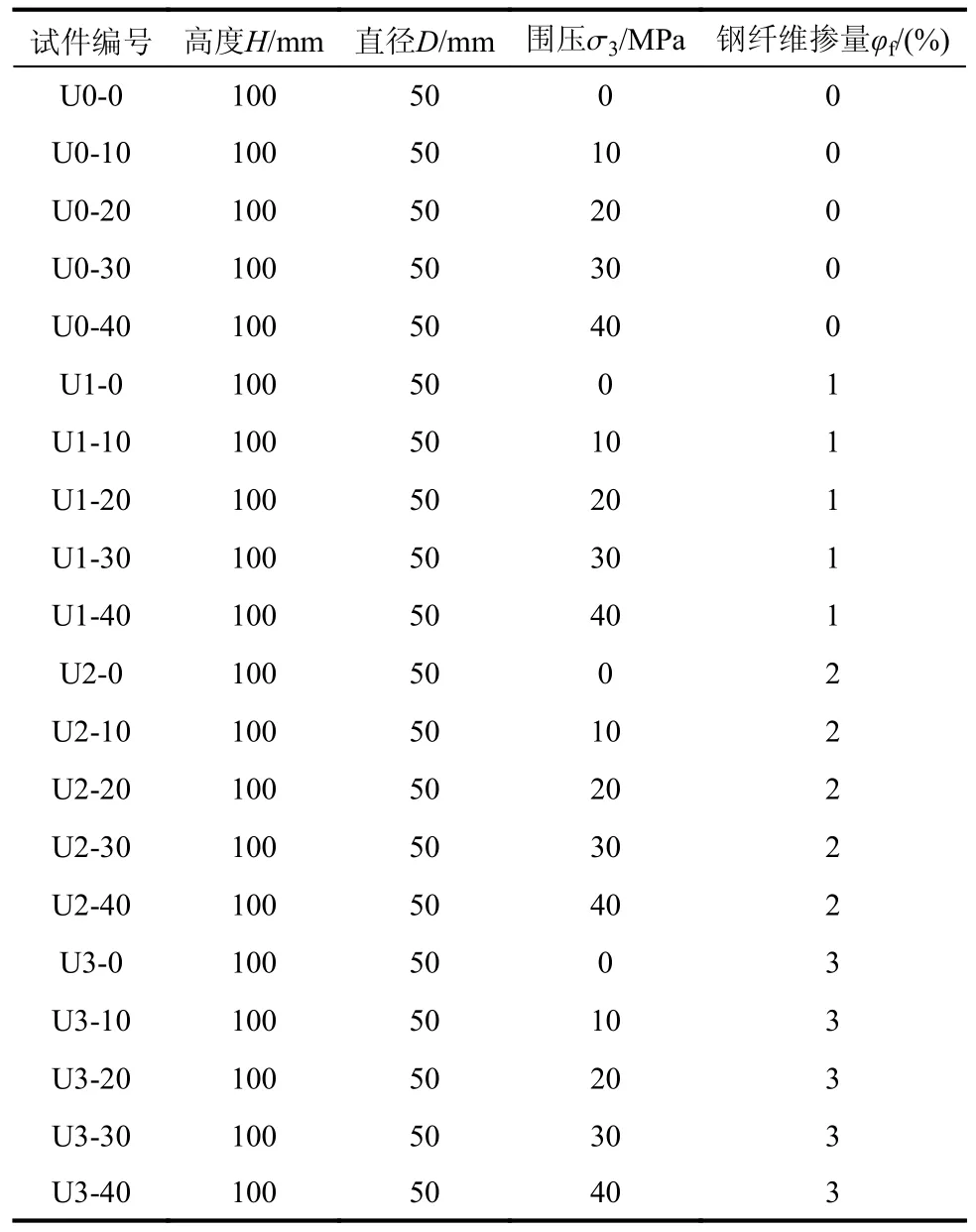
表1 UHPC 常规三轴试验参数一览表Table 1 List of UHPC conventional triaxial test parameters

1.2 配合比和试件制备

本文UHPC 的水胶比为0.16，由水泥、硅灰、石英砂、减水剂、水以及钢纤维等组成，具体配合比如表2 所示。

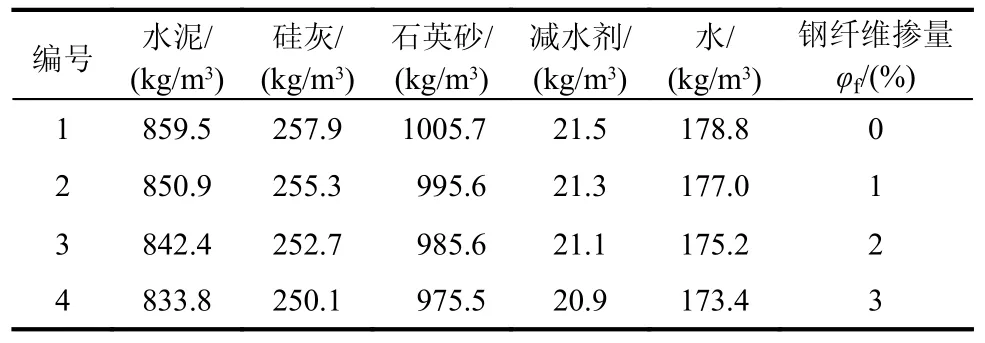
表2 UHPC 配合比一览表Table 2 List of UHPC mix proportion

UHPC 试件的表面状况对三轴压缩试验的成功至关重要，因为在高油压下，即使是隐藏在试件表面下方的正常孔隙也很容易被油压穿透。使得隔离套被油压穿破，导致试件侧面与硅油直接接触，从而硅油穿透在压缩下可能出现的裂缝，并在试件内部起到劈裂作用。为了使试件尽量减少试件表面不良状况给试验结果带来的不利影响，本文采用水泥浆填充所有相对较大的孔隙。

UHPC 试件是在福州大学土木工程学院结构馆预制场浇筑，采用尺寸为φ50 mm×100 mm 一端开口一端闭口的可拆卸圆柱体塑料模进行浇筑。试件浇筑完成后静置24 h，拆除模具，对其表面进行处理，而后将其置于常温环境，养护3 天并保持湿润，将其进行90 ℃高温蒸养72 h。养护好的试件置于常温环境中直至加载，将养护完成后的UHPC 圆柱试件置于岩石打磨机上进行端部打磨，确保试件加载时端部平整，并在试验前3 天采用水泥浆填补试件表面孔洞。

2 试验设备和加载方式

2.1 试验设备

本次试验采用RTX-1500 电液伺服低温高压动态岩石三轴测试系统，该系统主要包括高压三轴室、围压/孔压增压器、轴/环向应变测量装置(引伸计)、动力源以及空气增压机等，其中高压三轴室以及围压/孔压增压器如图1 所示。高压三轴室内径为150 mm，可以承受轴向3000 kN 最大荷载和最大140 MPa 围压，对应于围压/孔压增压器可以给压力室施加最大压力，试件尺寸需满足直径50 mm 以及高度100 mm，压力室中上压盘带有一个球座来补偿试件的不平行端面，且带有轴向和径向变形测量系统。试验人员通过电脑控制轴力和围压的加卸载，轴力由与装置轴向作动器相连的油泵施加，围压则由与三轴压力室相连的围压增压器施加，电脑主机与三轴试验系统自带主机连接，通过控制主机，进而给各个装置进行反馈操作。

图1 岩石三轴测试系统主要装置照Fig.1 Main device photo of rock triaxial testing system

2.2 加载方式

本次试验载全程采用应变控制加载，采用轴向应变为0.02 %/min 的加载速率进行轴向加载。荷载施加步骤为：以1 MPa/s 的加载速度施加围压至目标值，保持围压恒定不变，轴向以0.02 %/min应变加载至曲线下降段，待曲线下降至80%峰值应力或者出现下降段曲线突降时，设置软件自动停止加载或手动控制停止加载。图2 为荷载加载路径图，其中σ1为轴向应力，σ2和σ3为围压。

由于试件表面存在较小孔隙，为了避免施加围压时，硅油通过渗入孔洞而降低试件承载力，采用内径52 mm 壁厚0.7 mm 黑色热缩管将试件包裹保护。加载过程中试件的轴向和环向应变通过轴向和环向引伸计传感器与底座相连进行测量，轴向应变为试件整体压缩应变，取两侧测量的轴向应变平均值，环向应变由布置在试件中间的环向引伸计传感器测得的试件整体环向压缩应变。图3 为安装完应变传感器后的试件。

图3 试件装样照Fig.3 Specimen photo

3 试验结果和分析

3.1 破坏形态

图4 为UHPC 在常规三轴压缩后的破坏形态，除了钢纤维掺量为0%且围压值较小的部分试件以及围压为零的其他钢纤维掺量试件手动停止加载外，其他试件在设置加载结束条件时，均设置为应力-应变曲线下降到峰值应变80%时停止加载。钢纤维掺量不为0%的试件，当围压为零时，仅仅依靠钢纤维的抗拉拔效应，无法阻止试件过度开裂，因此在加载后期，出现试件较大的开裂声。当围压不为零时，由于钢纤维的抗拉拔作用以及围压给试件施加的约束作用，整个加载阶段不出现混凝土开裂声，且随着钢纤维掺量和围压的增大，这种现象越明显。钢纤维掺量不变围压较小时，试件破坏时有贯穿试件轴向且较为明显的斜向主裂缝，次裂缝较少，且随着钢纤维掺量的增大变得更少。围压较大时，试件主要出现端部挤压破坏现象，且随着围压的增大，端部会出现较多的小裂片，可以看出钢纤维掺量保持不变时，UHPC 试件的破坏形态由明显的斜剪破坏过渡到挤压破坏。这与过镇海[27]对混凝土多轴试验分析的结果对应，即混凝土的破坏形态分别为拉断、柱状压坏、片状劈裂、斜剪破坏以及挤压流动5 种。

图4 试件破坏形态图Fig.4 Specimen failure mode

钢纤维掺量为0%的试件在加载后期，轴向应变下降到80%峰值应变之前，由于没有钢纤维的抗拉拔作用，围压不足以阻止UHPC 的开裂，因此在加载后期出现明显的混凝土开裂声，且围压越小，声音越重。当围压为零时，试件在加载到峰值应变时，承载力变急剧下降，UHPC 失去承载力，试件整体产生多条贯穿柱身的轴向主裂缝，因而产生爆裂破坏现象。随着围压的增大，约束效应增强，试件破坏时逐渐呈现贯通柱身的斜剪破坏并伴随多根次裂纹，以及贯穿柱身的“Y”字型裂缝破坏，整体呈剪切破坏现象。

图5 对比了围压为10 MPa 时不同钢纤维掺量试件破坏现象，可以看出，所有试件都呈剪切破坏现象，柱身有一条明显的贯穿斜向主裂缝，且随着钢纤维掺量的增大，UHPC 延性不断提高，开裂速度减缓，脆性破坏现象越来越弱，因此其斜裂缝的斜角度越来越明显，破坏现象越不明显。

图5 围压为10 MPa 时不同钢纤维掺量试件破坏形态图Fig.5 Specimen failure patterns of different steel fiber content with the confining pressure of 10 MPa

3.2 应力-应变曲线

3.2.1 围压大小影响

本次试验中，轴向作动器测得的轴力为试件承载力与施加的油压力之和，轴向应力等于试件自身在轴向荷载及围压共同作用下轴向应力(即偏应力)与围压之和。因此，在分析围压UHPC 轴压性能时，应采用偏应力进行分析，而不是作动器测得的轴向应力，但为了便于分析，本文将试验得到的偏应力统称为轴向应力。图6 为不同围压大小的UHPC 试件轴向应力-轴向(环向)应变曲线。

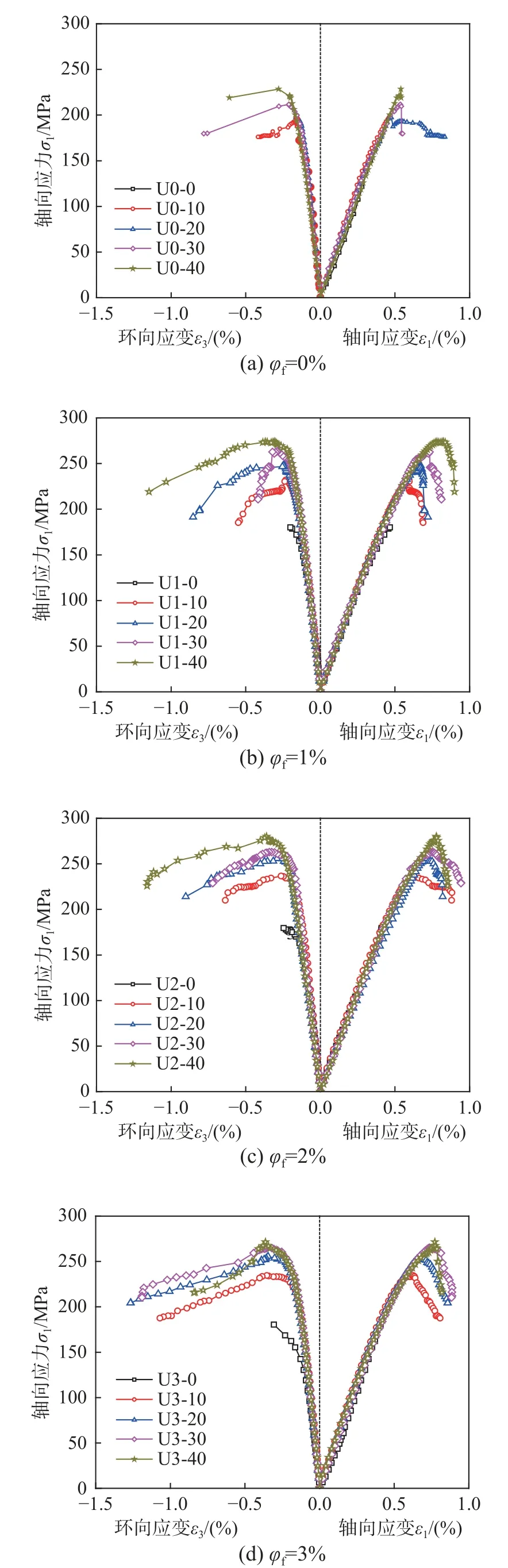
图6 不同围压UHPC 应力-应变曲线对比图Fig.6 Comparison of stress-strain curves of UHPC with different confining pressure

由图6 可知，在弹性加载阶段，轴向应力和应变及环向应变呈线性增长趋势。随着荷载继续增大，应力发展至90%峰值应力处，试件由内部微裂纹逐渐发展成外部裂纹，导致应力增长减慢，应变增长速度增大，试件进入弹塑性阶段，且该阶段持续时间较短，这与普通混凝土有很大区别[28]。在达到峰值应力后，轴向应变快速增长，试件承载能力减小，进入破坏阶段，不断增大扩展的裂纹使环向应变迅速增长，试件最终由于裂纹开裂过于迅速而丧失承载能力。围压为零的试件呈脆性破坏，且随着围压增大破坏速度减缓，趋于延性破坏。当钢纤维掺量不变且围压不为零时，应力-应变曲线在弹性变化过程中受围压大小影响较小，且与围压为零时试件弹性模量几乎相等，说明有无围压对UHPC 弹性模量的影响是可以忽略的，这与一些研究者对NSC 的研究结果[29-30]一致。曲线下降段随着围压增大下降速度减缓，轴向应变发展速度减小，分析其原因为：围压对试件承载能力起正向作用，在开裂后，围压力的存在减缓了试件表面裂缝发展速度，抑制其开裂。

3.2.2 钢纤维掺量影响

图7 为不同钢纤维掺量UHPC 试件轴向应力-轴向(环向)应变曲线。由图7 可知，当围压保持不变时，钢纤维掺量由0%增大至1%时，曲线峰值应力增大较大，说明有无钢纤维对UHPC 强度影响较大；但随着钢纤维掺量增大，曲线峰值应力变化不大，说明钢纤维掺量由1%变化到2%时，试件承载能力变化较小，但曲线下降段环向应变发展越来越慢，加载过程变长，试件承载时间变长，说明钢纤维掺量增大有利于延缓试件破坏，延性更好。由图7 还可知，相等围压不同钢纤维掺量的UHPC 试件的弹性模量随着钢纤维掺量的变化几乎保持不变，说明钢纤维掺量对其影响可以忽略不计。

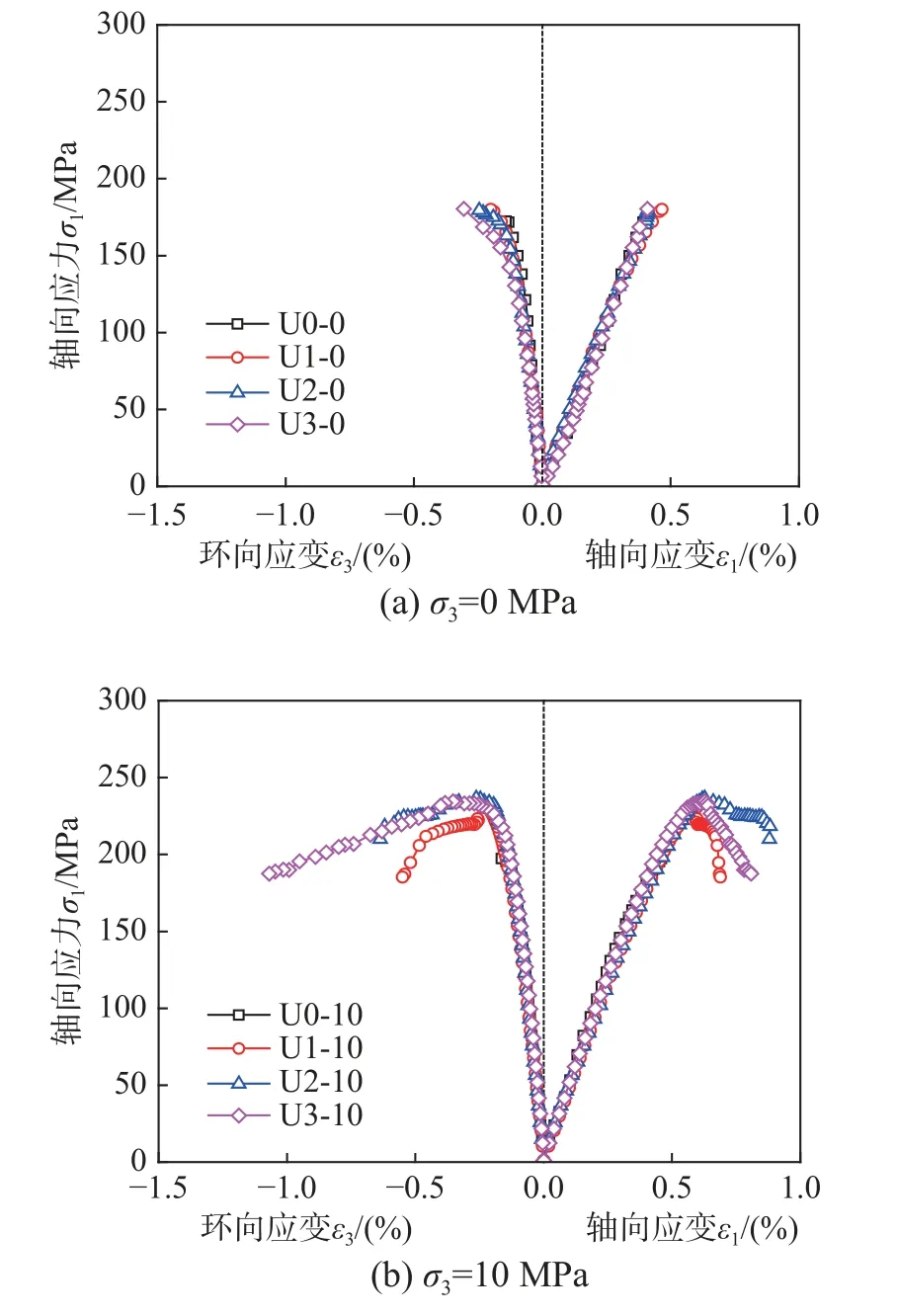
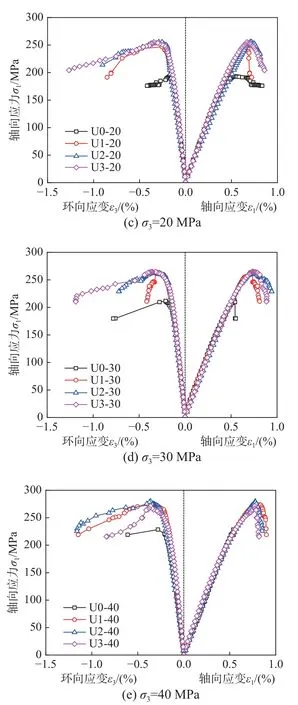
图7 不同钢纤维掺量UHPC 应力-应变曲线对比图Fig.7 Comparison of stress-strain curves of UHPC with different steel fiber content

3.3 峰值应力和应变

3.3.1 围压大小影响

图8 为围压大小对UHPC 试件峰值应力的影响图，具体的峰值应力和应变结果如表3 所示。可知，随着围压的增大，峰值应力呈增大趋势，为了方便比较，取同一围压等级下不同钢纤维掺量试件平均峰值应力进行比较。围压由0 MPa 增大至40 MPa 时，UHPC 试件平均峰值应力由179.5 MPa增大至266 MPa，增大了48.19%，说明钢纤维掺量不变时，围压的变化对UHPC 试件峰值应力影响较大。

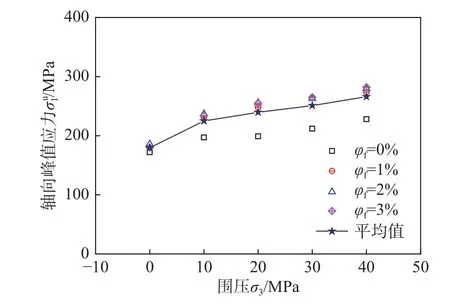
图8 围压大小对峰值应力影响图Fig.8 Effect of confining pressure on peak stress

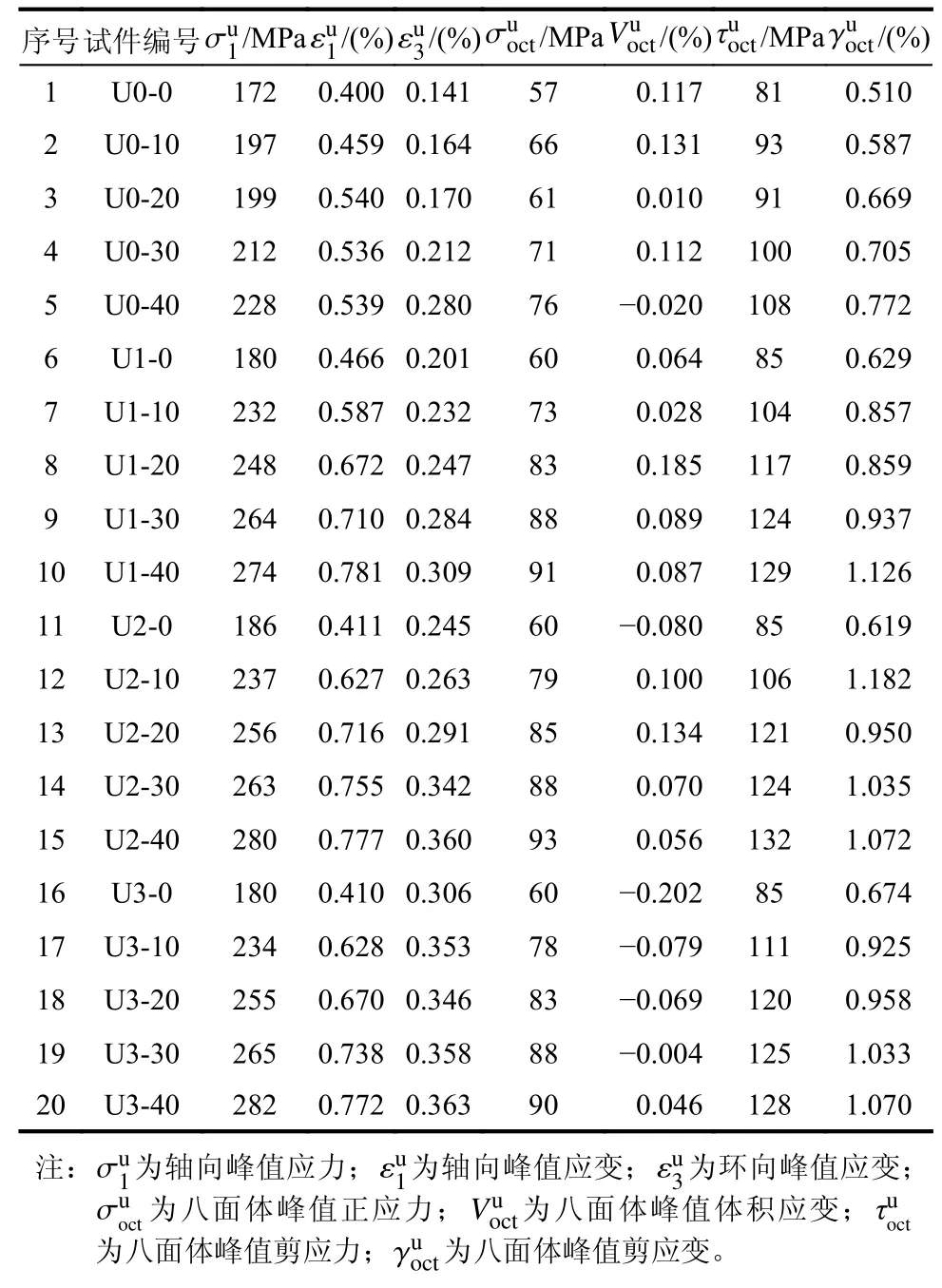
表3 试验结果一览表Table 3 Experimental results list

图9(a)和图9(b)分别为围压对轴向和环向峰值应变的影响图。结合表3 和图9(a)可知，围压为零的试件，轴向峰值应变分布在0.4%～0.5%，而有围压的试件应变分布在0.5%以上，区别较大。本文采用每组围压的轴向峰值应变平均值进行比较，对于围压由0 MPa 增大至40 MPa 时，轴向峰值应变由0.42%增大至0.72%，增大了70.07%。结合表3 和图9(b)可知，同样取环向峰值应变平均值进行对比分析，围压由0 MPa 增大至40 MPa 时，环向峰值由0.23%增大至0.33%，增幅达43.48%，几乎呈线性增长趋势。对比两图可知，围压对轴向峰值应变影响较大，能有效抑制竖向裂缝发展。

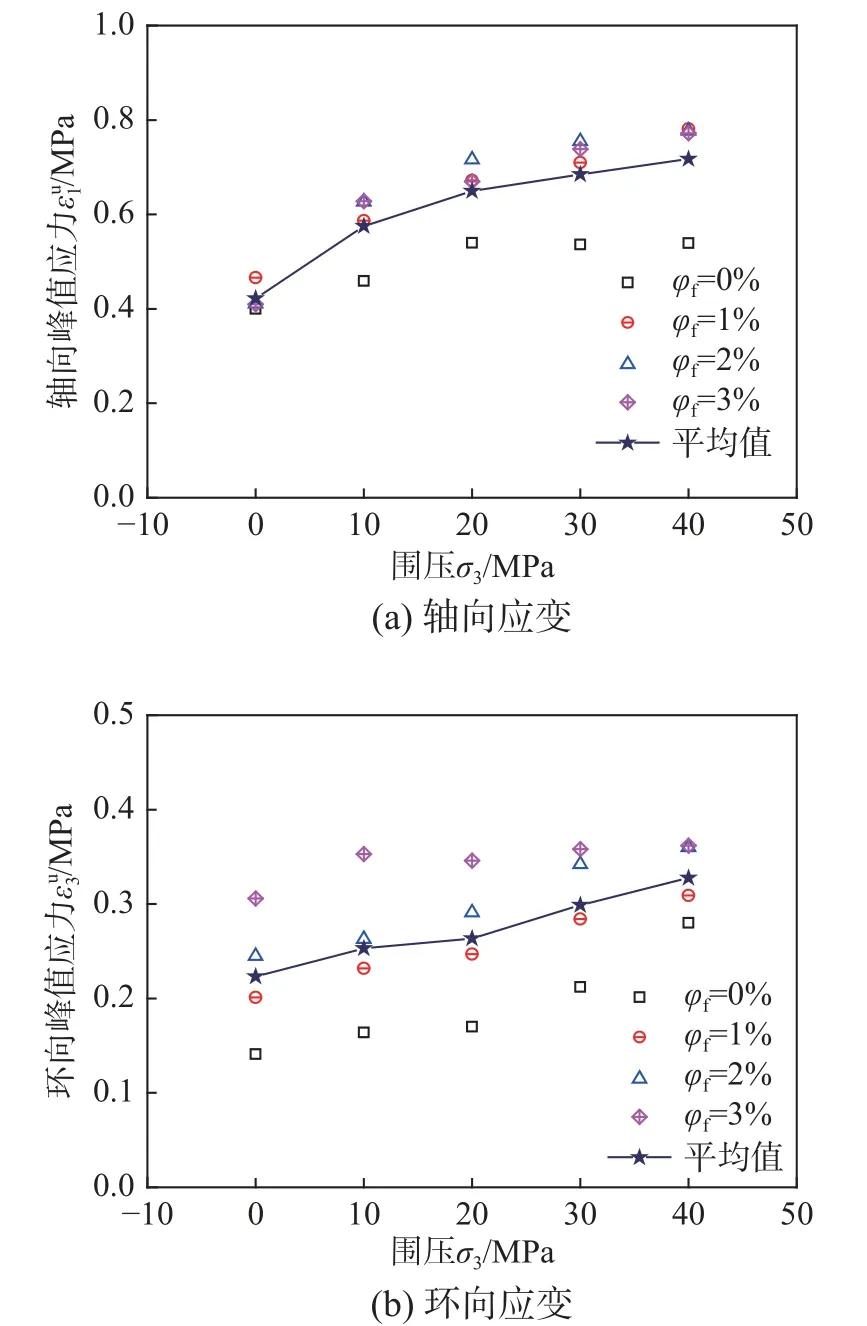
图9 围压对峰值应变影响图Fig.9 Effect of confining pressure on peak strain

3.3.2 钢纤维掺量影响

图10 为钢纤维掺量对UHPC 试件轴向峰值应力的影响图，结合表3 可知，钢纤维掺量由0%增加至1%时，峰值应力变化较大，当钢纤维掺量由1%分别变化至2%和3%时，峰值应力变化不大。

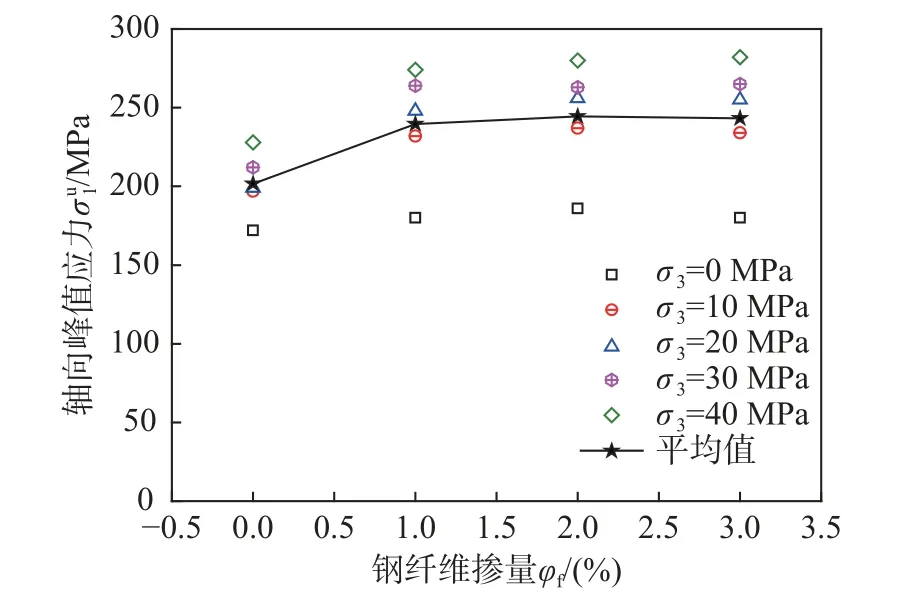
图10 钢纤维掺量对轴向峰值应力影响图Fig.10 Effect of steel fiber content on axial peak stress

为了方便比较，本文对每一组钢纤维掺量对应的峰值应力取平均值进行对比。钢纤维掺量由0%增加至1%时，峰值应力由201.6 MPa 增大至239.6 MPa，均值增大了18.85%；对比其他不同钢纤维掺量的峰值应力均值，几乎不变。因此，对于三轴压缩UHPC 试验中，有无钢纤维对峰值应力影响较大，而不同钢纤维掺量则几乎无影响。

图11(a)和图11(b)分别为钢纤维掺量对轴向和环向峰值应变的影响图。结合表3 和图11(a)可知，钢纤维掺量为0%的试件，轴向峰值应变分布在0.2%～0.4%，而有掺钢纤维的试件应变分布在0.4%以上，区别较大。本文采用每组钢纤维掺量的轴向峰值应变平均值进行比较，对于钢纤维掺量由0%增大至2%时，轴向峰值应变由0.52%增大至0.66%，增大了26.92%；钢纤维掺量由2%增大至3%时，轴向峰值应变由0.66%减小至0.64%，减小了3%，减小不大，但总体上呈先增大后减小趋势，在钢纤维掺量2%处最大，分析其原因可知：在轴压和围压双重作用下，过量的钢纤维掺量对UHPC 内部产生过约束，在减缓开裂速度的同时，降低了峰值应变。结合表3 和图11(b)可知，同样取环向峰值应变平均值进行对比分析，钢纤维由0%增大至3%时，环向峰值应变几乎呈线性增长趋势，由19.3%增大至34.5%，增长了78.76%。对比两图可知，钢纤维掺量对环向峰值应变影响较大，能有效抑制环向裂缝发展。

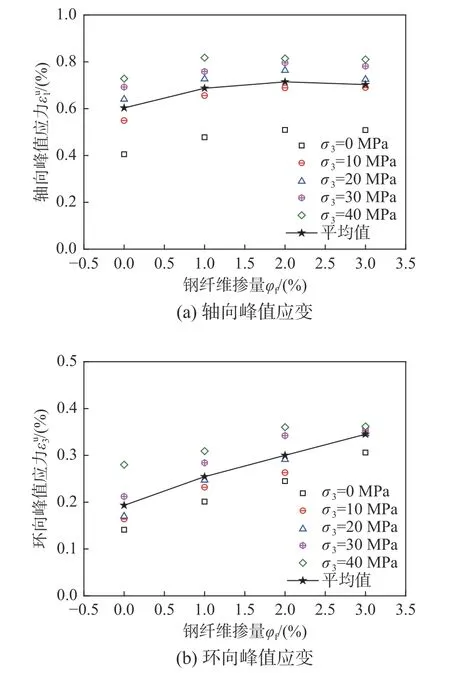
图11 钢纤维掺量对峰值应变影响图Fig.11 Effect of steel fiber content on peak strain

4 八面体应力-应变关系曲线

以上所讨论的应力-应变定量曲线比一般的三轴应力-应变曲线更能反映具体的应力-应变变化趋势。为了适用于更复杂的实际情况，还需要绘制其他类型的应力-应变曲线，其中包括八面体应力-应变关系。而八面体应力-应变关系包括以下两种：八面体正应力-体积应变关系、八面体剪应力-剪应变关系，其中八面体正应力和体积应变分别采用式(1)和式(2)进行计算，八面体剪应力和剪应变分别采用式(3)和式(4)进行计算：

式中： σoct为八面体正应力；Voct为八面体体积应变；τoct为八面体剪应力； γoct为八面体剪应变；σ1为第一主应力，本文指轴向应力； σ2和 σ3分别为第二和第三主应力，本文指围压； ε1为第一主应变，本文指轴向应变； ε2和 ε3分别为第二和第三主应变，本文指环向应变。

4.1 八面体正应力-体积应变关系曲线

图12 为钢纤维掺量保持不变时，不同围压下UHPC 的八面体正应力和体积应变之间的关系。

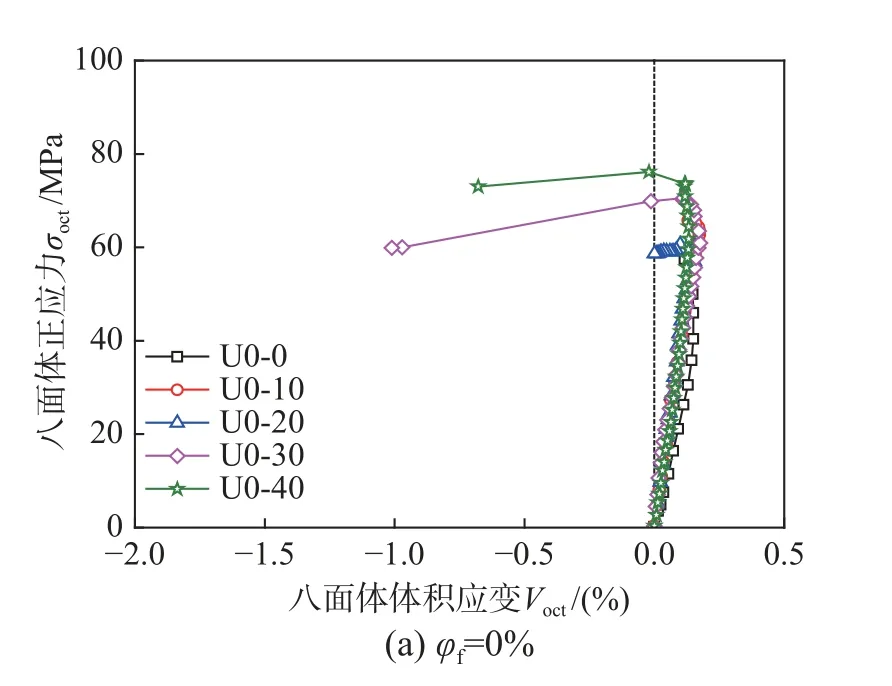
图12 不同围压八面体正应力-体积应变曲线图Fig.12 Octahedral normal stress-volumetric strain curves with different confining pressure

图12 中所有曲线的主要相似之处在于UHPC应力达到轴向峰值应力之前(约95%)开始膨胀。在达峰值荷载前，变形以受压应变为主，在此前，体积应变随荷载增加而增加。随着荷载继续增加，受拉应变逐渐增加使总的体积应变逐渐减小，在峰值后，体积应变转变为以受拉应变为主，即呈现体积应变负值状态。在下降段，UHPC 体积显著膨胀，轴向应力略有下降，表明UHPC 内部裂纹扩展剧烈。八面体正应力与膨胀开始前的体积变化呈线性关系，体积模量保持不变。图13 为在保持围压不变时，不同钢纤维掺量下UHPC 八面体正应力与体积应变曲线之间的差异。在UHPC开始膨胀之前，比例荷载倾向于更平滑坡度变化。

图13 不同钢纤维掺量下八面体正应力-体积应变曲线图Fig.13 Octahedral normal stress-volumetric strain curves with different fiber content

4.2 八面体剪应力-剪应变关系曲线

保持钢纤维掺量不变，不同围压下UHPC 八面体剪应力-剪应变关系如图14 所示。由图14 可知，曲线基本上遵循相同的趋势，如果通过其各自的八面体峰值剪应力和峰值剪应变对其进行归一化，可以看出随着围压的增大，峰值剪应力和剪应变都不断增大，但下降段趋势几乎一致。

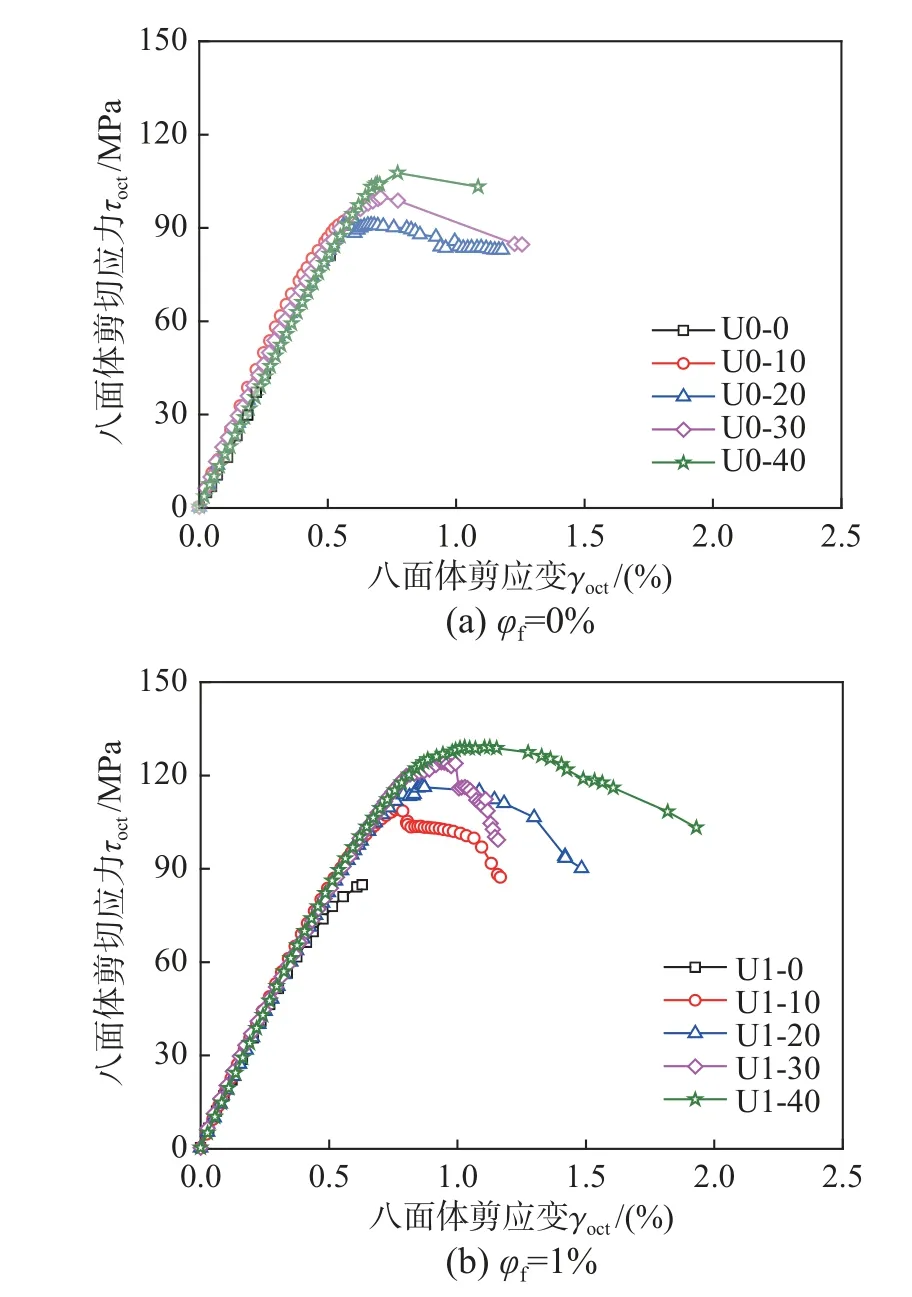
图14 不同围压八面体剪应力-剪应变曲线图Fig.14 Octahedral shear stress-shear strain curves with different confining pressure

图15 为保持围压不变时不同钢纤维掺量下UHPC 的剪应力-剪应变曲线对比图。可以看出不同钢纤维掺量下，但剪应力-剪应变曲线上升段呈线性发展趋势，且不同钢纤维掺量下的曲线几乎重合，说明其在弹性阶段对UHPC 剪切模量影响不大。当钢纤维掺量由0%增大至1%时，剪应力有明显的增大，钢纤维掺量在1%～3%变化时，剪应力和剪应变都变化不大，说明钢纤维掺量对三轴压下UHPC 的抗剪能力作用较小。

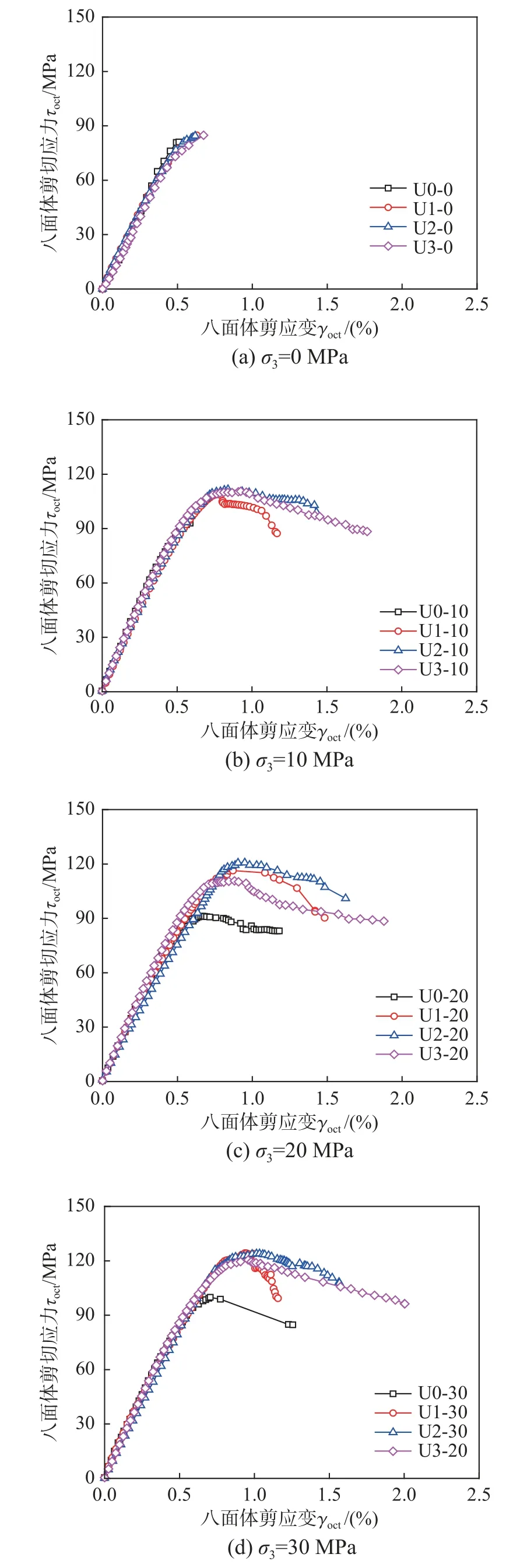
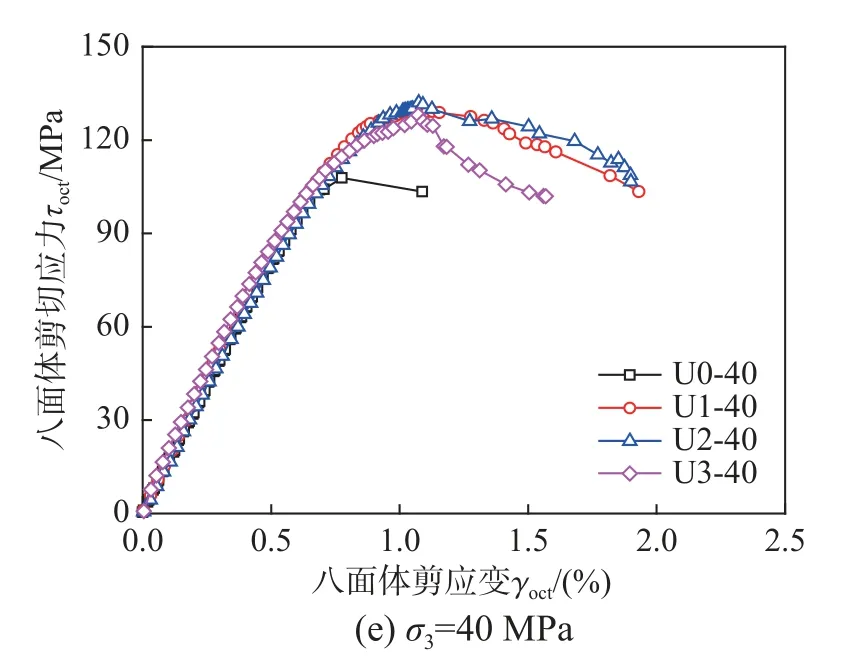
图15 不同钢纤维掺量下八面体剪应力-剪应变曲线图Fig.15 Octahedral shear stress-shear strain curves with different steel fiber content

5 UHPC 八面体破坏准则

国内外已有大量针对混凝土破坏准则的研究，如Mohr-Coulomb 二参数准则、Bresler-Pister 三参数准则、Willam-Warnker 五参数准则等，可通过这些准则对混凝土应力空间的破坏包络面进行描述，从而判断其破坏和强度。本文通过对三轴受压下UHPC 八面体应力-应变进行分析，得到如表3 所示的试验结果一览表，并分析得到八面体峰值正应力和峰值剪应力的关系曲线如图16 所示，并采用如式(5)所示的Drucker-Prager 二参数准则对UHPC 八面体破坏准则进行分析，得到式(6)所示计算式。

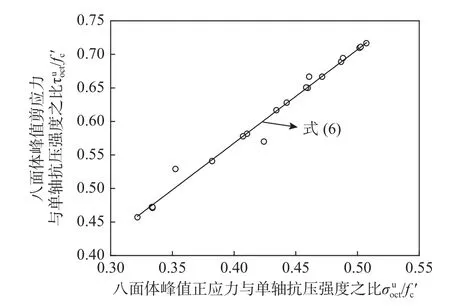
图16 UHPC 八面体峰值正应力与峰值剪应力关系Fig.16 Octahedral peak normal stress and peak shear stress curves of UHPC

由图16 和式(6)可以看出，UHPC 在八面体应力空间的剪应力与正应力成线性关系，且八面体峰值剪应力随着八面体峰值正应力增大不断增大。

6 结论

本文以围压和钢纤维掺量为试验参数，针对UHPC 开展了三轴受压试验，得到以下结论：

(1)围压和钢纤维掺量均为零的试件破坏时呈劈裂破坏，其他试件则呈剪切破坏。围压不变时，随着钢纤维掺量增大，试件破坏时主裂纹斜角度越来越明显，破坏形态越不明显；钢纤维掺量不变时，随着围压的增大，试件破坏形态由明显的斜剪破坏过渡到挤压破坏。

(2)试件加载过程分为弹性段、弹塑性段和破坏段三个过程。应力-应变曲线下降段随围压增大下降速度不断减缓，轴向应变发展变慢；随着钢纤维掺量增大，峰值应力变化不大，但下降段环向应变发展变慢，试件承载时间变长，延性更好。

(3)随着围压增大，UHPC 轴向和环向峰值应变呈线性增长；钢纤维掺量由0%增大至1%时，峰值均应变增大了18.85%，钢纤维掺量由1%增大至3%时，无太大变化；轴向峰值应变随钢纤维掺量增大呈先增大后减小趋势，在2%处最大；环向峰值应变呈线性增长趋势。

(4)对UHPC 八面体正应力-体积应变关系、八面体剪应力-剪应变关系进行分析，并建立UHPC八面体破坏准则关系式。