金属网在刚性弹头静压下的力学性能分析

黄祺临，汪 敏，陈辉国，周 帅

(陆军勤务学院军事设施系，重庆 401311)

金属网是指由钢丝编织成的三维网状结构(图1)[1]，因其具有重量轻、力学性能优异等特点，在工程领域应用愈加广泛。在交通工程中，应用金属网作为主要组成构件的防护装置(如被动防护网、主动防护网等)，用于拦截落石、泥石流等自然灾害[2-3]；在建筑工程中，采用金属网对钢筋混凝土结构构件进行加固，提高构件的承载能力和延展性等[4-6]；在防护工程中，增设金属网加强钢筋混凝土结构抗侵彻、抗爆炸等防护性能[7-8]，利用金属网作为拦截飓风中风力卷起的碎片，从而降低撞击户外门窗而引起的破坏等[9-10]。随着编织用钢丝强度、韧性等的提高，利用高强钢丝编织而成的金属网在轻型坦克或装甲车的格栅装甲中也得到了应用(图1～图2)，主要目的是用于拦截近程武器(如火箭弹、迫击炮弹等)的打击，提高战时轻型坦克或装甲车的生存概率[11-13]。

图1 金属网格栅装甲Fig.1 Wire nets grille armor

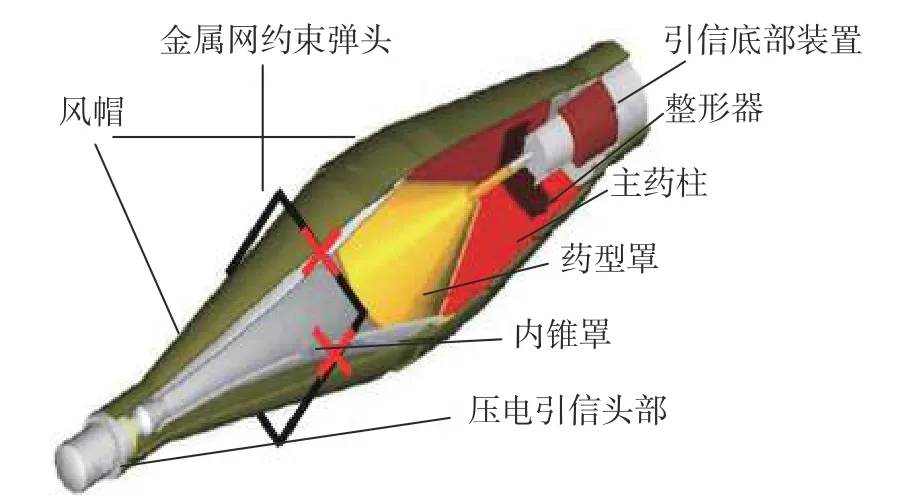
图2 弹头与金属网间的相互作用Fig.2 Interaction between the warhead and the wire nets

关于高强金属丝编织而成的金属网，相关力学性能研究较多，但主要集中在落石灾害防治领域。在静力性能研究方面，主要考虑金属网平面内双向拉伸性能[14]、平面外抗顶破性能等[15-16]。然而，为提高金属网拦截近程武器的效率，金属网在弹头静压下的力学性能研究是一个重要的工作，这对于理解金属网与弹头相互作用下的力学性能和破坏特点，合理设计金属网的网孔尺寸和规格等都具有较好的指导意义。

图3 中给出了金属网的实弹拦截试验及破坏情况。从图中可以看出，金属网在弹体打击作用下的破坏局限于单个网孔区域，这与落石冲击金属网存在明显的区别[17]。从目前的研究成果看，现阶段关于金属网的抗顶破性能试验，主要是根据落石灾害实际情况而设计的试验装置和试验方法，获得金属网在顶破作用下的荷载-位移曲线和承载力理论计算方法[18]，为落石灾害防护中的金属网选型和设计提供参考。但根据落石灾害特点而设计的金属网试验条件与弹头和金属网相互作用的状态差别较大，对研究金属网在弹头静压下力学性能的借鉴作用有限。

图3 金属网的实弹拦截试验及破坏情况Fig.3 Short-weapon intercepted tests and the fracture feature of the wire nets

基于以上原因，为研究金属网在弹头静压下的力学性能，结合金属网的实弹拦截试验情况和破坏特点，设计了刚性弹头加载装置和金属网静压试验平台，开展了直径为82 mm 和107 mm 的弹头加载装置静压金属网的试验，分析了金属网的破坏特点。此外，在试验研究的基础上，建立了刚性弹头加载装置静压金属网的理论模型，推导了刚性弹头加载装置静压金属网临界荷载的理论计算方法，研究成果可为金属网拦截弹体的初步设计提供参考依据。

1 刚性弹头静压金属网的试验设计

1.1 刚性弹头加载装置和金属网的设计

由于近程武器种类繁多，形状各异，根据典型近程武器的外形和试验加载条件[19]，设计了口径为D=82 mm和D=107 mm两类刚性弹头加载装置，前半部分按弹头外形制作，后半部分为弹头支撑部分，用以保证试验的正常进行。弹头加载装置的布置及具体尺寸如图4(a)所示，制作的刚性弹头加载装置见图4(b)。

图4 刚性弹头加载装置尺寸及照片Fig.4 Dimensions and photos of rigid warhead loading device

根据弹体口径，设计了金属网的尺寸，如图5所示。图中：d为编网钢丝直径；x为沿水平方向菱形网孔短边尺寸；y为沿竖直方向菱形网孔长边尺寸； β为菱形网孔锐角；Di为网孔内切圆直径；ht为沿平面外法线方向外边界厚度；hi为内净厚度。金属网近似为正方形，nL≈1 m，nQ≈1 m。试验中，共设计了2 种钢丝直径编织而成的金属网，具体参数见表1(由于金属网为松散结构，因此表中为拉紧后的尺寸)。

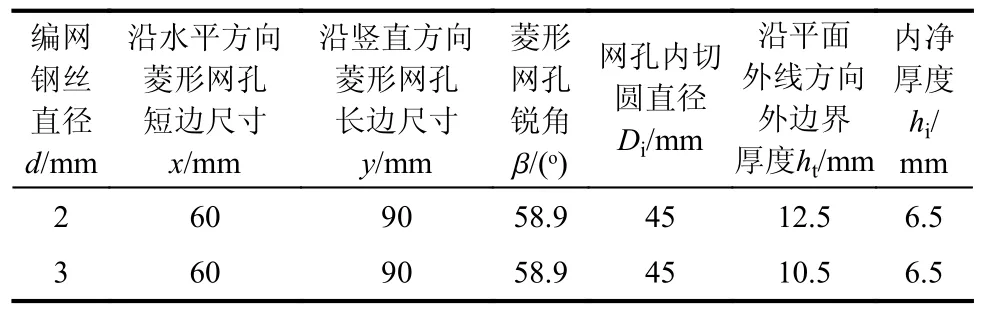
表1 金属网规格尺寸参数Table 1 Size parameters of the wire nets

图5 金属网规格尺寸图Fig.5 Specification and dimension drawing of wire nets

1.2 静压试验平台设计

设计的静压试验平台如图6(a)所示，外轮廓尺寸为2 m×2 m×1.5 m，其中主要部件为金属网悬挂与张拉装置，如图6(b)所示。

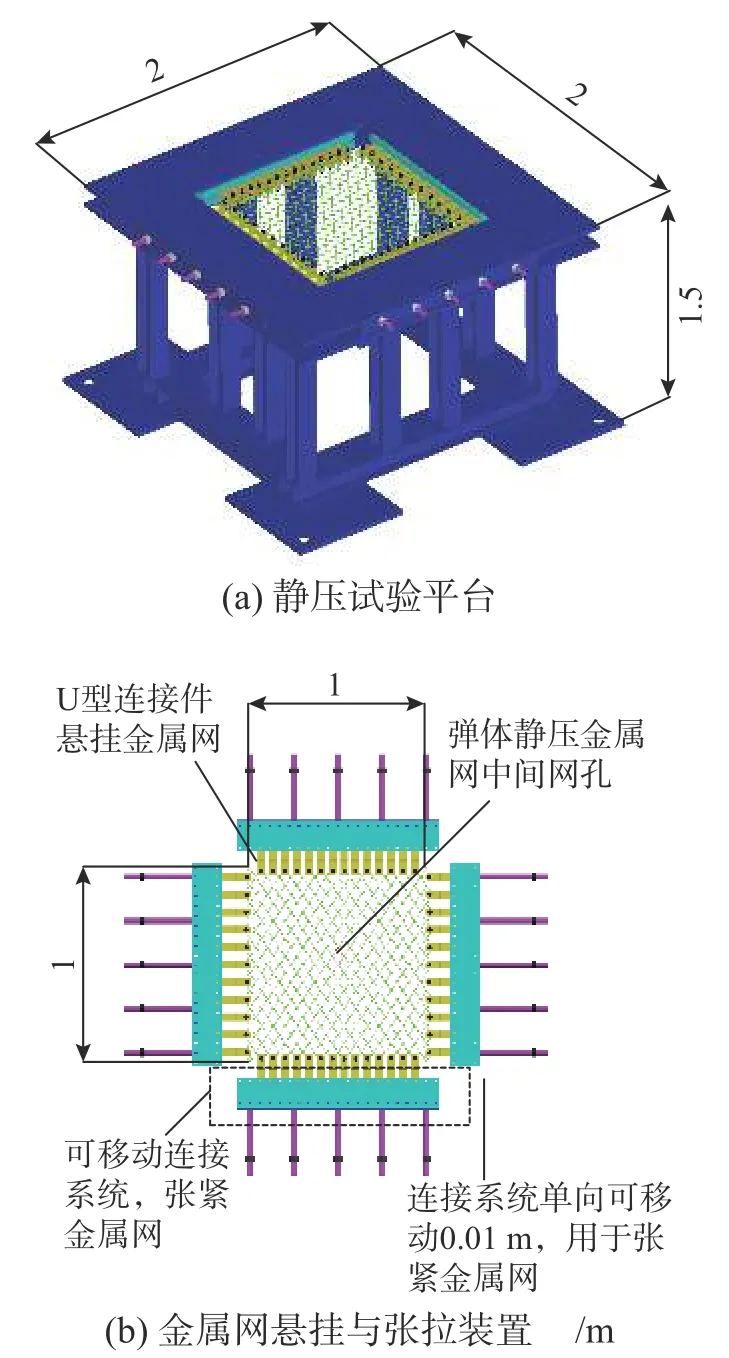
图6 金属网静压试验平台尺寸及细部图Fig.6 Dimensions and details of static pressure experimental platform for the wire nets

金属网悬挂与张拉装置分为两部分：一部分为连接金属网的U 型连接件；另一部分为可移动连接系统。U 型连接件可以固定金属网的四个边界，约束金属网平面内的自由度；可移动连接系统可以对金属网进行张拉，单侧单向可张拉约0.01 m，这样可以保证每次试验前，金属网均处于张紧状态。试验平台可开展1 m×1 m 金属网的静压试验。

1.3 试验加载方案设计

考虑到金属网的几何大变形特性，静压试验在20 kN 液压试验机上进行，液压试验机行程为500 mm。试验开始前将弹头加载装置的连接板与试验机端承板连接，弹头对准金属网中间菱形网孔的中间位置(见图6(b)、图7)。

图7 刚性弹头加载装置安装照片Fig.7 Installation photo of rigid warhead loading device

根据金属网规格(表1)和加载弹头直径情况(图4)，开展了2 类金属网、2 类弹头加载装置共8 次破坏性试验，具体如表2 所示。试验时，弹头加载装置下压采用位移速率控制，即弹头以匀速慢慢往下压，弹体的下压速度为10 mm/min。当弹头与金属网接触、弹头受到反向荷载作用时，记录弹体向下的位移与反向荷载，待金属网破坏后即停止加载，读取并绘制荷载-位移曲线。

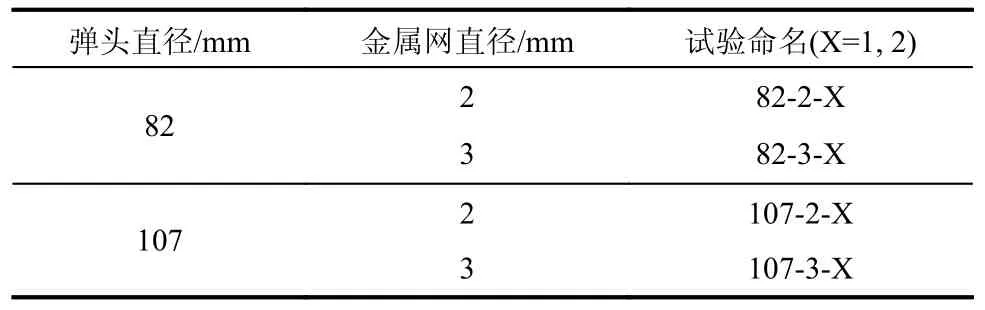
表2 静压试验加载方案Table 2 Test loading scheme for static pressure

2 静压试验结果分析

根据试验情况，可以将金属网与刚性弹头加载装置间的相互作用分为以下4 个状态(图8)。

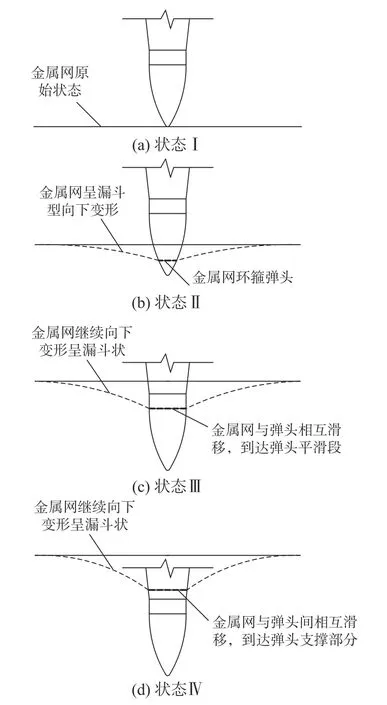
图8 金属网与刚性弹头加载装置间相互作用的状态图Fig.8 State diagram of interaction between the wire mesh and the rigid warhead loading device

状态Ⅰ：弹头加载装置缓慢向下移动，弹头前端与金属网平面接触。

状态Ⅱ：弹头部分居中垂直插入金属网菱形网孔中，金属网中菱形网孔被弹头挤压逐步扩大，同时逐渐变成弹头剖面形状并环箍住弹头。当金属网环箍作用力达到一定程度时，金属网与弹头一起向下移动，金属网整体变形呈现漏斗型。

状态Ⅲ：随着金属网中菱形网孔在弹头环向挤压和竖向拉伸共同作用下，菱形网孔进一步扩大，造成网孔对弹头的环箍力无法限制金属网与弹头之间的相对位移，金属网随着弹头继续向下变形的过程中，与弹头发生相对位移。

状态Ⅳ：金属网在随着弹头继续向下变形的过程中，与弹头也存在一定程度上的相对位移，到达弹头加载装置的支撑部分。

由于金属网与弹头加载装置间的相互作用比较复杂，金属网不断受到加载装置向下静压的运动过程中，分为整体变形和局部变形。整体变形为金属网受到的漏斗型拉伸变性，局部变形为金属网中菱形网孔受到的弹头挤压变形。在这个过程中，金属网的网孔尺寸和弹头的直径等对静压过程均有影响。根据弹头直径的不同，金属网所经历的状态也有所区别。

对于82 mm 弹头的静压试验，金属网的变形均经过了图8 所示的四个状态，进入状态Ⅳ后，与弹头接触部分的菱形网孔中钢丝交接处发生断裂，状态Ⅱ、状态Ⅳ的情况如图9 所示。对于107 mm弹头的静压试验，金属网的变形仅经历了图8 所示的两个状态，由状态Ⅱ到状态Ⅲ的过度过程中，与弹头接触部分的网孔发生破坏。

图9 金属网与弹头相互作用的试验照片Fig.9 Test photos of interaction between the wire mesh and the warhead

82 mm 弹头和107 mm 弹头静压金属网造成的破坏形态基本一致。图10 中给出了典型的金属网在弹头加载装置静压下的破坏照片，从图中可以看出，除了与弹头加载装置接触部分的菱形网孔发生变形，逐步接近于弹头剖面形状直至破坏外，其余部分的网孔基本保持为菱形；接触部分的菱形网孔破坏位置均位于钢丝交叉节点处。对比图3和图10 可以看出，实弹打击和刚性弹体静压金属网的破坏形态基本一致，其最终破坏均仅局限于网孔与弹体接触部位。

图10 金属网网孔破坏后照片Fig.10 Photos of the wire mesh after fracture

图11～图12 中分别给出了82 mm 弹头和107 mm弹头加载装置静压金属网的荷载-位移曲线图，对比分析图11～图12 可以看出：

图11 82 mm 弹头加载装置静压金属网的荷载-位移曲线Fig.11 Load displacement curves of static pressure for the wire mesh of 82 mm rigid warhead loading device

图12 107 mm 弹头加载装置静压金属网的荷载-位移曲线Fig.12 Load displacement curves of static pressure for the wire mesh of 107 mm rigid warhead loading device

1) 82 mm 弹头加载装置静压金属网的荷载-位移曲线经历上升-下降/近似平稳-上升三个阶段。在第一个上升阶段，弹头存在3 个状态，第一个状态的峰值荷载发生时，金属网位于弹头加载装置的平滑段起始部分(对应图8 中的状态Ⅲ)；第二个状态，金属网在弹头平滑段时，由于此处弹头直径保持不变，竖向荷载突然降低，并保持一段距离(对应图8 中由状态Ⅲ转换到状态Ⅳ的过程)；第三个状态，荷载随着弹头加载装置的向下位移，逐步增大，直到金属网发生破坏(对应图8中的状态Ⅳ)。

2) 对于107 mm 弹头静压金属网，竖向荷载随着弹头加载装置的向下位移逐渐增大，直到破坏(对应图8 中的状态Ⅰ和状态Ⅱ)。

3) 82 mm 弹头静压作用下，随着约束弹头的菱形网孔逐步扩大，金属网与弹头间存在滑移、平衡、滑移反复过程，因此，竖向荷载随着弹头下压位移的增大，增长趋势比较平缓；而在107 mm弹头的作用下，由于金属网与弹头间滑移较小，金属网中菱形网孔在拉伸、挤压共同作用下发生了破坏。

3 刚性弹头静压金属网的理论分析

3.1 理论分析模型及计算方法

在刚性弹头加载装置静压金属网的试验中，由于弹头静压装置作用在金属网中间位置的单个菱形网孔中，菱形网孔的四个边为对称受力，因此可利用金属网中菱形网孔单元的对称性，建立理论模型进行分析进行计算。

根据图8 所示状态，当金属网中菱形网孔与弹头相互位置在图13 中A-A 所示位置时，金属网中单个菱形网孔中钢丝发生断裂(即由状态Ⅱ过度到状态Ⅲ的过程中)，此时，可认为弹头A-A 剖面为金属网临界破坏面。

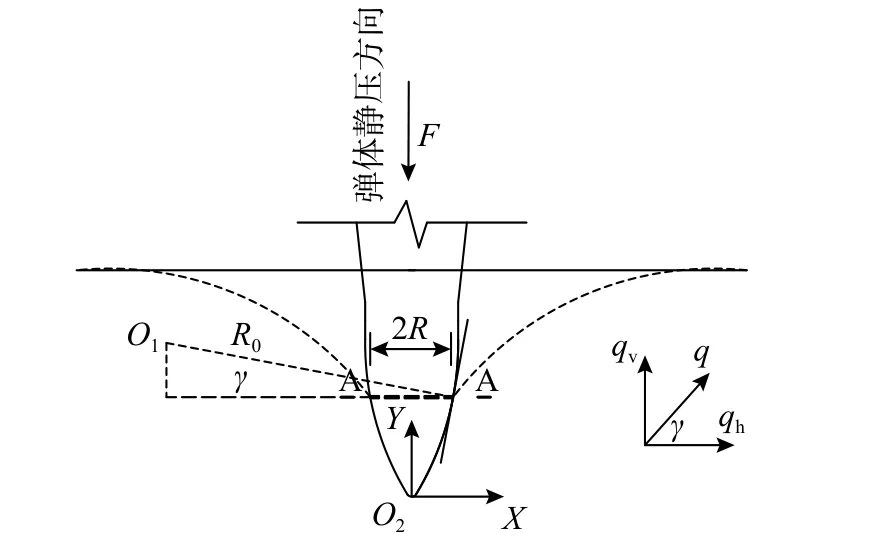
图13 弹头与金属网相互作用位置示意图Fig.13 Schematic diagram of interaction position between the warhead and the wire mesh

取与弹头接触部分菱形网孔的一个微段进行力学分析，假设此微段受到弹头的作用力q沿着弹头部分与金属网接触部位的切线方向，则可以把作用力q分解为两个方向的力：一个是水平方向，为微段受到的弹头扩张力qh(根据作用力与反作用力原理，即为菱形网孔对弹头的环箍力)；另一个是竖直方向，为金属网抵抗弹头加载装置向下运动的力qv(也即弹头受到的竖向荷载)。因此，根据图13所示的受力分析图，可得弹头受到的竖向荷载为：

式中， γ为摩擦角。

根据弹头部分的形状参数特征，通过几何分析可得正切摩擦角：

式中：R0为弹头部分的曲线半径；x0为弹头部分的曲线圆心O1横坐标；R为临界破坏面(A-A 剖面)弹头的半径(设计弹头剖面为圆形)。

由于弹头加载装置与金属网相互作用时，弹头加载装置被套箍在金属网的单个菱形网孔内，直至菱形网孔中的钢丝破断，且初始为菱形的单个网孔会随着弹头加载装置的逐渐下压而与弹头加载装置部分充分接触。为需考虑金属网中的菱形网孔与弹头加载装置之间的相互作用，取A-A剖面进行分析(图14)。

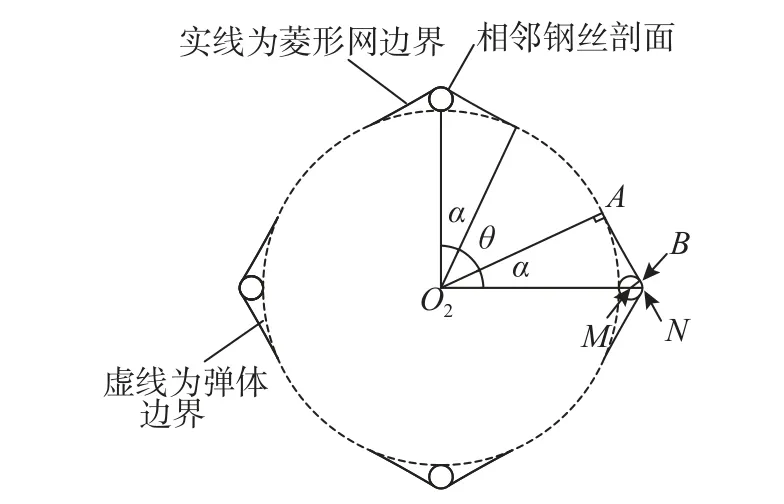
图14 弹头作用于菱形网孔A-A 剖面示意图Fig.14 Schematic diagram of section A-A of warhead acting on diamond mesh

从图14 中可以看出： ΔO2AN～ΔMBN，因此，有如下等式成立：

故有：

简化式(4)，可得弹头与金属网1/4 非接触段半角余弦为：

因此，弹头与金属网接触角为：

式中，d为钢丝直径。

取图14 中1/4 弹头范围进行分析，绘制几何关系如图15 所示。

图15 1/4 弹头范围内接触几何关系示意图Fig.15 Schematic diagram of contact geometry within the range of 1/4 warhead

通过几何相互关系，可得弹头与菱形网孔接触部分的长度为：

在忽略与临近钢丝接触部分误差情况下(即忽略与图15 中小圆接触部分和金属网平面外的尺寸情况下)，1/4 弹头范围内钢丝总长为：

联立式(8)、式(9)可得：

式中：x菱形网孔短边尺寸；y菱形网孔短边尺寸；l为菱形网孔单边边长。

考虑该1/4 弹头范围内受力情况，弹头与金属网中菱形网孔接触段受力情况如图16 所示。

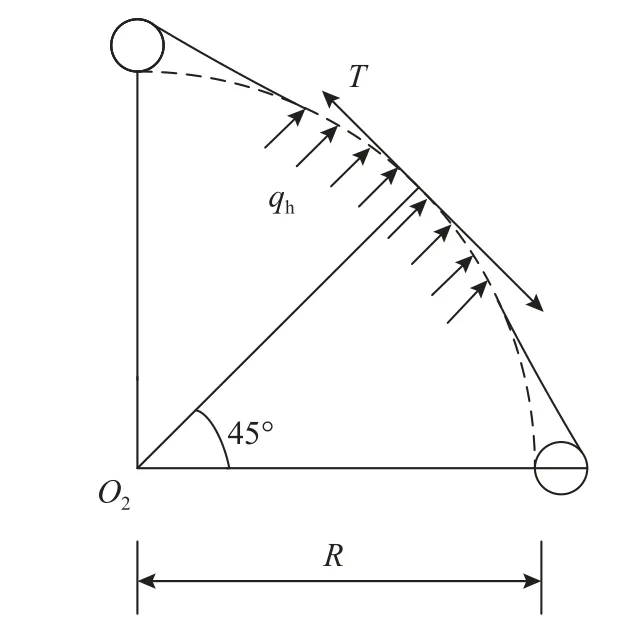
图16 接触段受力示意图Fig.16 Schematic diagram of contact section stress

尽管考虑到弹头下压时金属网中的菱形网孔钢丝在交叉节点位置发生断裂(见图10 所示)，此时菱形网孔交接位置钢丝会受到轴力和弯矩的耦合作用[14]，但由于金属网的厚度很小，在钢丝交叉位置承受的弯矩也较小，同时综合8 次破坏试验的结果和试验现象可知，交叉处钢丝的断裂主要由轴力控制，因此可忽略弯矩对钢丝断裂的影响。

综合以上假设，设钢丝在单轴拉伸荷载下的破断力为T，根据图16 的计算简图，在45°对角线方向建立静力平衡方程有：

求解式(11)可得钢丝破断力为：

又由式(1)可得竖向荷载为：

求和即可得静压临界荷载：

联立式(5)、式(6)和式(11)，并代入式(14)进行整理，得到刚性弹体静压金属网的静压临界荷载为：

需要说明的是，对于82 mm 弹头加载装置静压金属网，当弹头加载装置的支撑部分与金属网网孔接触时(即进入状态Ⅳ以后)，金属网中单个菱形网孔中钢丝发生了破断，因此，相关的理论计算取弹头加载装置的支撑部分的几何特征形状进行分析，其理论推导过程与由状态Ⅱ过度到状态Ⅲ的基本一致。

3.2 算例分析

对2 mm、3 mm 高强钢丝进行了单轴拉伸试验，获得了高强钢丝的单轴拉伸工程应力-应变关系曲线，如图17 所示。从图17 中可以看出，2 mm和3 mm 高强钢丝的单轴极限抗拉应力基本一致，均约为1860 MPa。

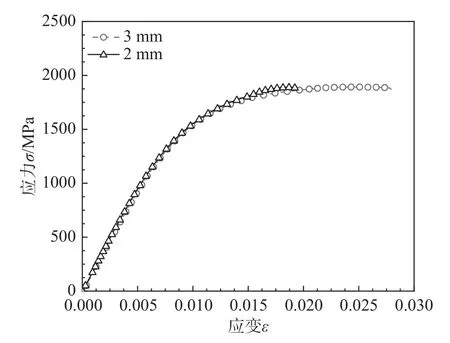
图17 高强钢丝单轴拉伸应力-应变关系曲线Fig.17 Uniaxial tensile stress-strain relationship curve of high-strength steel wire

结合图4 弹头相关尺寸和图5 金属网的相关参数，利用第3.1 节的理论计算方法，即可求得刚性弹头加载装置静压金属网的静压临界荷载，计算流程如图18 所示。

图18 计算流程Fig.18 Calculation flow chart

以107 mm 刚性弹头加载装置静压直径为3 mm的金属网为例进行计算。

1) 破坏临界半径。将图5 中金属网规格尺寸代入式(10)，可得临界半径：

2) 摩擦角。将图13 中弹头曲线参数代入式(2)，可得摩擦角正切值：

3) 非接触半角。根据图14 弹头作用于菱形网孔A-A 剖面示意图，代入式(5)，可得非接触半角：

4) 接触角。根据图14 剖面示意图，代入式(6)可得接触角：

5) 钢丝单轴拉伸极限破断力。按图17，3 mm高强钢丝的单轴拉伸的极限破断力：

6)刚性弹头静压临界荷载。综合前面的计算结果，代入式(15)，可得静压临界荷载：

按图18 计算流程和3.2 节的算例分析，计算了82 mm 和107 mm 弹头静压装置静压金属网的静压临界荷载，并与试验结果进行了对比，结果见表3。从表3 中可以看出，理论计算获得的静压临界荷载与试验结果非常接近，误差均在±10%以内。

表3 刚性弹头静压试验与理论计算比较结果Table 3 Comparison between static pressure tests and theoretical calculation by the rigid warhead

3.3 误差分析

由于金属网属于三维网状结构，与弹体作用的力学机理比较复杂，因此在试验研究的基础上，对理论分析模型进行了简化处理。对模型简化可能导致的误差进行分析如下：

1) 在试验过程中，与弹头相互作用的菱形网孔两侧交接节点位置，钢丝之间存在轻微的滑移，而上、下节点位置，钢丝之间的滑移不明显(图19)。这主要是由于，在试验开始前，设计的试验平台给金属网施加了初始预紧力，使得金属网处于张紧状态，同时由于弹头垂直作用在金属网正中心网孔位置，能在一定程度上降低钢丝间的滑移。因此，理论模型忽略了钢丝在交接节点位置滑移的影响，但这会减小临界破坏面弹头的半径，从而使得理论模型计算结果偏小。

2) 由于钢丝连接节点位置存在几何偏心，弹头静压金属网中间部位的网孔过程中，网孔四个节点位置钢丝均受到轴力和弯矩的耦合作用(图19)，虽然理论分析模型中忽略了弯矩的作用，会造成理论模型计算结果偏大，但因为金属网的破坏主要由轴力控制，且初始几何偏心很小，因此这方面的误差会很小。

3) 在试验过程中，与弹头作用的菱形网孔受到两个方面的荷载作用：一方面是弹头对网孔的挤压变形；另一个方面是网孔受到的周围其他菱形网孔中钢丝的拉伸变形。理论模型中忽略了拉伸变形的影响，会造成理论模型计算结果偏大。

总体而言，理论模型能有效地预测弹体静压金属网的临界荷载，误差满足工程许可范围。

4 结论与展望

结合金属网的实弹拦截试验情况和破坏特点，设计了刚性弹体静压金属网的试验方案，并开展了静压试验和理论分析，得到了如下结论：

(1) 金属网在刚性弹头静压作用下呈现整体变形和局部变形，整体变形呈现向下的漏斗型变形，局部变形主要集中在金属网与弹头接触的菱形网孔内，呈现逐步接近于弹头剖面形状的变形。金属网的破坏主要由局部变形控制，破坏位置位于菱形网孔钢丝交叉节点处。

(2) 基于金属网受弹头静压的试验现象及相关结果的研究，推导了刚性弹头静压金属网临界荷载的理论计算方法，分析了理论模型产生误差的原因。总体而言，理论模型计算结果与试验结果非常接近，误差均在±10%以内。

对比静压试验和实弹拦截试验，仅就金属网的破坏形态上来看，两者基本一致，其破坏均仅局限于网孔与弹体接触部位，金属网的整体变形对弹体承受的荷载影响不大。因此，理论计算方法可在一定程度上为金属网拦截弹体的初步设计提供参考。然而，金属网在弹体动态冲击作用下的影响因素很多，需要考虑高强钢丝和弹体材料在高应变率下的动态性能、弹体的冲击能量(速度、质量)等情况，而这些影响因素还需要结合静力理论分析成果开展深入的研究。