基于改进卡尔曼滤波的水产养殖无人船导航方法*

曹莉凌，尚 进，曹守启

（上海海洋大学工程学院，上海 201306）

0 引 言

实现无人船的高效精准导航，并对船体位置、速度实时控制，是实现水产养殖无人船自主巡航、智能投料、水质监测、水面巡检、科学喂养与高效管理的重要前提与保障［1］。惯性导航系统（inertial navigation system，INS）采用加速计测量载体的加速度，利用加速度积分项能够得到载体速度，但是随着时间推移，位置误差积累增加［2，3］。全球定位系统（global positioning system，GPS）［4，5］易受恶劣天气影响造成无人作业养殖船GPS信号弱。GPS／INS组合导航，总体性能远优于任一独立导航系统，是目前导航领域最为理想的导航组合方式［6］。

记忆渐消滤波是一种基于新息的自适应滤波方法，其核心是如何选取最佳的渐消因子值［7］。文献［8］中渐消因子推算过程繁杂，不易理解，不适合水产养殖无人船导航系统。文献［9］从新增益与历史增益关系入手，增加计算的未知变量，利用增益与预测协方差关系，得到渐消因子，计算过程忽视了量测方差值的影响。文献［10］自适应无迹卡尔曼滤波（unscented Kalman filtering，UKF）算法，结合最大后验概率估计准则和矩阵奇异值分解技术，计算过程繁琐且不易理解，对处理器运算能力要求高，不适合用在水产养殖无人船上。本文利用新息协方差计算值与新息协方差预测值之间关系确定渐消因子取值，显得更加简洁易懂，更适用于实际养殖无人船导航系统应用。

1 卡尔曼滤波算法模型

1.1 标准卡尔曼滤波模型

设定系统状态模型和观测模型分别为［11］

式中 Φk，k-1为状态转移矩阵，为k-1 时刻到k时刻的系统一步转移矩阵；Hk为观测矩阵，Φk，k-1和Hk均为雅可比矩阵，Xk为k时刻的状态向量，Zk为k时刻的观测量，Γk-1为系统噪声矩阵，Wk-1为系统噪声，Vk为量测噪声。

1.2 渐消卡尔曼滤波原理

当针对系统所建立的数学模型不精确或物理系统本身运行过程中发生改变，最新的观测数据比过去的观测数据更加能反映实际情况。采用滤波器使得，随着时间的增长逐渐“忘记”过去老的观测数据，这种滤波方法称为渐消因子滤波［7，12］。

系统状态一步预测表示为

式中为k时刻状态一步预测值，为k-1时刻的状态最优估计。k时刻状态值减去k时刻一步预测值可以得到状态一步预测误差。

针对系统状态一步预测均方误差，典型的嵌入渐消因子的方式有以下3种［13］

式中Pk-1为预测协方差阵，λk为渐消因子，且λk≥1，将滤波协方差膨胀λk倍，加重现实测量数据的状态估计的作用，从而避免滤波器发散。本文选取第二种方式，如式（5）所示，渐消因子在等式外，结构上具有一定优势［13］。

状态估计为

如果仅使用系统状态方程的状态一步预测去估计Xk并没有考虑到量测方程的任何信息，这导致估计精度不高，因此可令＝Zk-，为量测预测误差（即新息），Kk为待定的修正系数矩阵，来调节两种数据之间权重也就是滤波增益。

滤波增益为

状态估计均方差为

1.3 渐消因子分析

由于新息能反映真实量测值与估计量测值之间的关系，所以常用来衡量卡尔曼滤波器的滤波性能。

新息序列为

协方差阵为

当Kk最优时，新息序列是白噪声序列，而新息自协方差函数为

假如卡尔曼滤波最优，新息序列是白噪声序列，则Sk＝0，即新息序列不相关，处处保持正交，Kk为最优增益。假设＝λkPk，k-1＝αkCk。其中，Ck为理论为估计，λk为渐消因子，αk为标量因子。

文献［13］中新增益阵为

计算αk，首先要确定，由文献［9］得

对＝αkCk两边求迹运算，考虑到比例系数αk不宜小于1，得

把式（8）代入式（12）得

假定Pk，k-1和均为满秩，则等式两边先左乘，再右乘，得

如果Hk满秩，则

Pk，k-1＝λk［Φk，k-1Pk-1+Qk-1］代入（HkPk，k-1+Rk）＝，并且对等式两边求迹得

以上方法需要假设条件太多，而且计算过程复杂繁琐，不易理解。

1.4 简易的渐消因子选取方法

建模准确情况下，标准卡尔曼滤波的新息序列在理论上是白噪声

实际的新息时间序列估计方差等于式（14），但是求出的新息协方差是对历史信息求平均值，并不能实时得出当前时刻的信息。根据文献［13］对其改进如下

式中Z0为k＝0时的新息向量；经过修改后的不需要对历史信息求均值更能精确敏锐地反映当前时刻系统模型误差状态。

当滤波情况最优时，新息协方差的理论值应与新息协方差的预测值相等，即

文献［13］的改进算法中，系统中存在某些不明确的建模参数，随着滤波进行可能会导致新息失配。因此，本文在文献［13］改进算法的基础上，引入渐消因子实现系统的自适应调节，即

经移项，得

等式两边求迹，得

考虑到比例系数λk不宜小于1，可得

1.5 水产养殖无人船组合导航系统耦合方式

水产养殖无人船组合导航系统采用松耦合方式，因为松耦合导航结构在实际工程应用中易于实现且导航信息具有一定余度［14］。在位置、速度方式下GPS／INS松耦合组合导航误差模型中，选取惯性导航系统的位置误差（δL，δλ，δh）、速度误差（δVE，δVN，δVU）、姿态误差（φE，φN，φU）、陀螺仪（εx，εy，εz）、加速度计）的一阶马尔可夫过程共15个作为组合导航系统的状态变量，即

式中δL，δλ，δh分别为纬度、经度和高度误差；δVE，δVN，δVU分别为东向、北向和天向速度误差；φE，φN，φU分别为东向、北向和天向的3个姿态误差角；εx，εy，εz分别为三轴陀螺误差；分别为加速度计误差。

GPS／INS松耦合组合导航观测方程有2 组量测值，一组是位置量测值，即惯性导航系统给出的纬度、经度以及高度信息和GPS接收机给出相应位置信息的差值，另一组是惯导系统和GPS系统各方向上速度的差值。即

2 系统仿真分析

仿真无人船运行轨迹，再比较渐消因子卡尔曼滤波效果和标准卡尔曼滤波效果，比较渐消因子卡尔曼滤波是否比标准卡尔曼滤波在精度上有所改进。用轨迹发生器设计无人船初始位置为纬度2. 07°、经度0. 7°，初速度设为0.4 m／s，选取仿真时间600 s进行无人船行驶轨迹仿真，仿真轨迹如图1所示。

图1 无人船行驶轨迹

利用平台仿真实现了本文提出的渐消因子卡尔曼滤波及常规自适应卡尔曼滤波的导航算法，对水产养殖无人船在600 s行驶时间内经纬度位置误差及速度误差进行了对比。图2为基于扩展卡尔曼滤波（extended Kalman filtering，EKF）算法对无人船经度、纬度位置与速度误差的估计，图3为基于渐消因子的改进的强跟踪卡尔曼滤波（strong tracking Kalman filtering，STKF）算法对无人船经度、纬度位置和速度误差的估计。本文对图2和图3 位置与速度误差范围进行统计，其结果如表1。

表1 2 种算法误差估计（°）

图2 EKF算法速度、位置误差估计

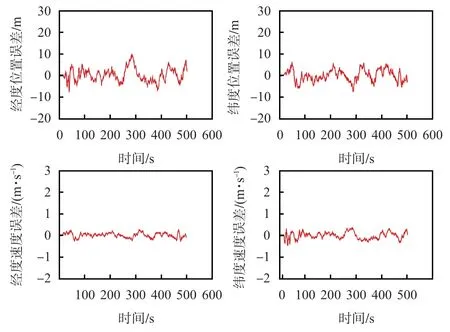
图3 STKF算法的位置和速度误差估计

通过表1在经纬度上的位置、速度误差估计数据对比，STKF算法比EKF 算法在位置误差估算方面，精度提高了1.6～3.3倍，在速度误差估算方面，精度提高了1.02～4倍。

3 结束语

本文提出的STKF算法，通过渐消因子在线调节预测协方差矩阵，间接调节增益矩阵，使滤波效果达到最佳效果。计算过程中增益值变化由预测协方差变化所致，直接利用理论新息协方差和预测新息协方差相等，直接计算渐消因子，通过渐消因子调节合适预测协方差值继而得到增益。这种方法计算量小，便于理解，误差精度上也比EKF 有一定改善。在水产养殖无人船导航中利用本文提出的渐消因子自适应卡尔曼滤波来融合INS和GPS 两种导航系统，适用性更强。