传递函数辨识(21):线性回归系统的递阶递推参数估计

丁 锋 ,刘喜梅

(1.江南大学 物联网工程学院,江苏 无锡 214122;2.青岛科技大学 自动化与电子工程学院,山东 青岛 266061)

辨识方法包括递推辨识和迭代辨识两类。因此结合递阶辨识原理,递阶辨识方法可分为递阶递推辨识方法和递阶迭代辨识方法两类。

递推辨识方法包括基本的随机梯度辨识方法、递推梯度辨识方法、递推最小二乘辨识方法、牛顿递推辨识方法等,所以结合递阶辨识原理,派生出递阶随机梯度辨识方法、递阶递推梯度辨识方法、递阶递推最小二乘辨识方法、递阶牛顿递推辨识方法等。有时省略“递推”二字,将“递阶递推辨识方法”简称为“递阶辨识方法”。

迭代辨识方法包括基本的梯度迭代辨识方法、最小二乘迭代辨识方法、牛顿迭代辨识方法等,所以结合递阶辨识原理,派生出递阶梯度迭代辨识方法、递阶最小二乘迭代辨识方法、递阶牛顿迭代辨识方法等。

将递阶辨识原理与辅助模型辨识思想相结合,诞生出的递推辨识算法包括辅助模型递阶随机梯度辨识方法、辅助模型递阶递推梯度辨识方法、辅助模型递阶递推最小二乘辨识方法、辅助模型递阶牛顿递推辨识方法等;诞生出的迭代辨识算法包括辅助模型递阶梯度迭代辨识方法、辅助模型递阶最小二乘迭代辨识方法、辅助模型递阶牛顿迭代辨识方法等。

将递阶辨识原理与多新息辨识理论相结合,诞生出的递推辨识算法包括递阶多新息随机梯度辨识方法、递阶多新息递推梯度辨识方法、递阶多新息递推最小二乘辨识方法、递阶多新息牛顿递推辨识方法等;诞生出的迭代辨识算法包括递阶多新息梯度迭代辨识方法、递阶多新息最小二乘迭代辨识方法、递阶多新息牛顿迭代辨识方法等。有时省略“递推”二字,将“多新息递推辨识方法”简称为“多新息辨识方法”。

将递阶辨识原理与辅助模型辨识思想、多新息辨识理论相结合,诞生出的递推辨识算法包括辅助模型递阶多新息随机梯度辨识方法、辅助模型递阶多新息递推梯度辨识方法、辅助模型递阶多新息递推最小二乘辨识方法、辅助模型递阶多新息牛顿递推辨识方法等;诞生出的迭代辨识算法包括辅助模型递阶多新息梯度迭代辨识方法、辅助模型递阶多新息最小二乘迭代辨识方法、辅助模型递阶多新息牛顿迭代辨识方法。

在连载论文中,使用多新息辨识理论、递阶辨识原理、耦合辨识概念[1-6],先后研究了信号模型、传递函数的参数估计[7-15]。递阶辨识是一种基于分解的辨识。一些两阶段辨识方法、三阶段辨识方法、多阶段辨识方法也可称为递阶辨识方法,如《系统辨识——辅助模型辨识思想与方法》第3、4、5章中的基于分解的辨识方法[4],《系统辨识——多新息辨识理论与方法》第2、3、4、5章中的基于分解的辨识方法、两阶段辨识方法和三阶段辨识方法[6]。本工作首先介绍线性回归系统(即白噪声干扰下的线性参数系统)的递阶递推最小二乘辨识方法,参见《自动化学报》1999年第5期上的原始论文“大系统的递阶辨识”[16]。在此基础上,结合多新息辨识理论,研究线性回归系统的递阶梯度辨识方法和递阶最小二乘辨识方法等。文中提出的递阶辨识方法可以推广用于其他线性和非线性随机系统,以及信号模型的参数辨识[17-26]。

1 递阶最小二乘辨识方法

考虑下列线性回归系统,

其中y(t)∈ℝ是系统输出变量,υ(t)∈ℝ是零均值随机白噪声,θ∈ℝn为待辨识的参数向量,φ(t)∈ℝn是由时刻t以前的输出y(t)和时刻t 及以前的输入u(t)等变量构成的回归信息向量。假设维数n已知。不特别申明,设t≤0时,各变量的初值为零,这里意味着y(t)＝0,φ(t)＝0,υ(t)＝0。

辨识的目的是利用观测信息{y(t),φ(t)}和某种优化算法估计系统的未知参数向量θ。尽管递推最小二乘算法能够估计参数向量θ,但由于大系统维数高、变量和待估计的参数数目多,使得算法的计算量和存储量急剧增加,以致在算法的实现上造成极大的困难,这就是所谓的“维数灾”。在这种情况下,研究基于分解的大系统递阶辨识算法,提出计算量小的辨识算法已成为必然。

为了说明递阶辨识算法能大幅度减小计算,下面先简单介绍辨识线性回归系统(1)的递推最小二乘辨识算法作为比较,随后推导递阶最小二乘辨识算法。

1.1 递推最小二乘辨识方法

1.1.1 递推最小二乘辨识算法

对于线性回归系统(1),定义随时间t 递增的准则函数为

极小化准则函数J1(θ),可以得到估计参数向量θ 的递推最小二乘算法(recursive least squares algorithm,RLS算法):

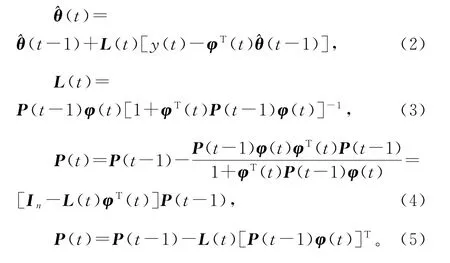
1.1.2 加权递推最小二乘辨识算法

在RLS算法(2)～(5)中引入加权因子wt,便得到估计参数向量θ 的加权递推最小二乘算法(weighted recursive least squares algorithm,WRLS算法):

1.1.3 遗忘因子递推最小二乘辨识算法

在RLS算法(2)～(5)中引入遗忘因子λ,便得到估计参数向量θ 的遗忘因子递推最小二乘算法(forgetting factor recursive least squares algorithm,FF-RLS算法):

1.1.4 加权遗忘因子递推最小二乘辨识算法

在RLS算法(2)～(5)中引入加权因子wt和遗忘因子λ,便得到估计参数向量θ 的加权遗忘因子递推最小二乘算法(weighted forgetting factor recursive least squares algorithm,W-FF-RLS算法):

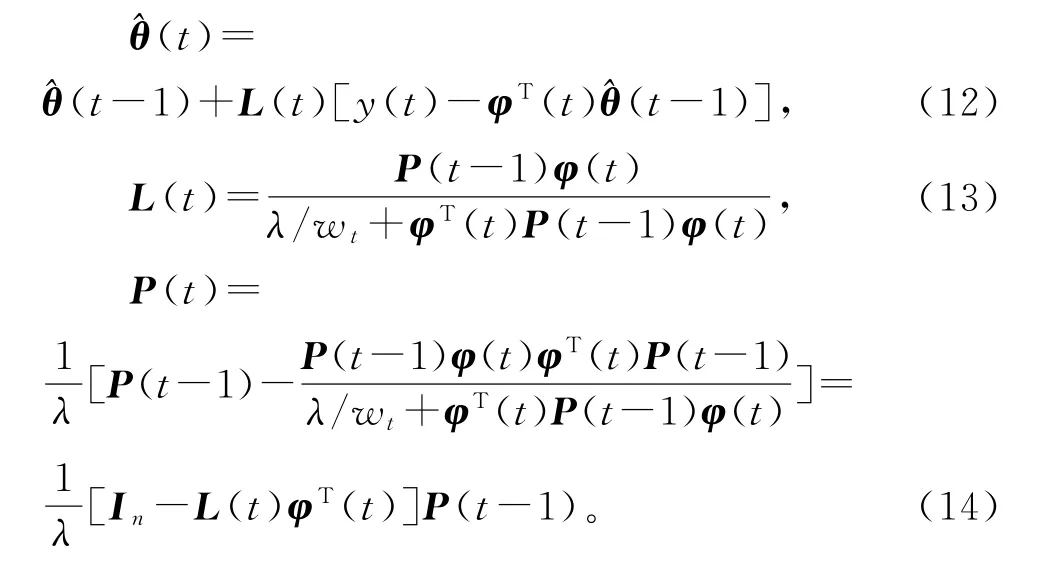
1.2 递阶最小二乘辨识算法

递阶辨识原理与辨识方法是笔者1996年给清华大学硕士生、博士生讲授《大系统理论及应用》课程时,受大系统递阶控制的“分解—协调原理”的启发提出的,把“分解”的思想引入辨识中,从而提出了递阶辨识原理,开辟了递阶辨识研究领域。

递阶辨识原理分3步。

第1步:辨识模型分解为一些子辨识模型。

第2步:采用最小二乘原理或梯度搜索原理等分别辨识这些子模型。

第3步:协调处理各子辨识算法间的关联项。

递阶辨识原理不仅能够解决大规模多变量系统辨识方法计算量大的问题,而且能解决结构复杂非线性系统的辨识问题。递阶辨识最初用于解决维数高、参数数目多的线性回归系统辨识算法计算量大的问题。首篇代表性论文“大系统的递阶辨识”发表在《自动化学报》1999年第5期上,随后递阶辨识原理发展用于类多变量受控自回归系统的辨识,代表性论文“多变量离散时间系统传递函数阵参数的递阶梯度迭代辨识方法与递阶随机梯度辨识方法”发表在国际期刊Automatica 2005年第2期上,“多变量系统传递函数模型的递阶最小二乘迭代辨识方法与递阶最小二乘辨识方法”发表在国际期刊IEEE Transactions on Automatic Control 2005年第3期上。以下介绍大系统(1)的递阶最小二乘辨识方法[2-3]。

将大系统(1)的信息向量和参数向量分解为N个维数为ni的子信息向量(sub-information vector)φi(t)和子参数向量(sub-parameter vector)θi如下:

于是,可以把系统(1)分解为N 个虚拟子系统(fictitious subsystem),即子辨识模型(sub-identification model,Sub-ID 模型),也称为递阶辨识模型(hierarchical identification model,H-ID模型):

极小化准则函数J2i(θi),利用递阶辨识原理,我们能够获得估计子参数向量θi的递阶最小二乘算法(hierarchical least squares algorithm,HLS 算法)[2,16]:

1.3 加权递阶最小二乘辨识算法

在递阶最小二乘算法(20)～(24)中引入加权因子wt≥0,便得到估计系统(1)参数向量θ 的加权递阶最小二乘算法(weighted hierarchical least squares algorithm,W-HLS算法):

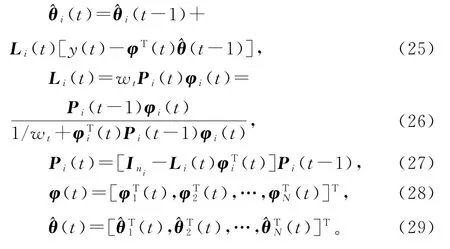
加权最小二乘算法对不同时刻的观测数据给予不同的权重,数据可信度大的给予的权值就大。如果某一时刻的权值取为零(wt＝0),说明此数据不可信,参数估计不进行刷新,而保持上一时刻的估计值,这可从此时刻的增益向量Li(t)为零看出。

1.4 遗忘因子递阶最小二乘算法

在递阶最小二乘算法(20)～(24)中引入遗忘因子0＜λ≤1,便得到估计系统(1)参数向量θ 的遗忘因子递阶最小二乘算法(forgetting factor hierarchical least squares algorithm,FF-HLS算法):

1.5 加权遗忘因子递阶最小二乘算法

在递阶最小二乘算法(20)～(24)中引入加权因子wt≥0和遗忘因子0＜λ≤1,便得到估计系统(1)参数向量θ 的加权遗忘因子递阶最小二乘算法(weighted FF-HLS algorithm,W-FF-HLS算法)或遗忘因子加权递阶最小二乘算法(forgetting factor W-HLS algorithm,FF-W-HLS算法):

2 递阶多新息最小二乘辨识方法

2.1 递阶多新息最小二乘算法

设整数p≥1为新息长度。借助多新息辨识理论[6],基于递阶最小二乘算法(20)～(24),定义堆积输出向量(stacked output vector)Y(p,t),堆积信息矩阵(stacked information matrix)Φ(p,t)和堆积子信息矩阵Φi(p,t)如下:

式(44)～(46)和(40)～(42)构成了辨识系统(1)参数向量θ 的递阶多新息最小二乘算法(hierarchical multi-innovation least squares algorithm,HMILS算法):

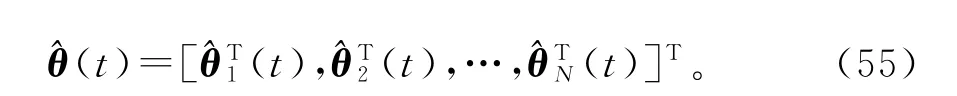
当新息长度p＝1时,HMILS算法(47)～(55)退化为HLS算法(20)～(24)。当子系统数目N ＝1时,HMILS算法退化为多新息最小二乘(MILS)算法[6]。当新息长度p＝1,子系统数目N ＝1时,HMILS算法退化为RLS算法(2)～(5)。

2.2 加权递阶多新息最小二乘算法

在HMILS算法(47)～(55)中引入加权因子wt,便得到辨识系统(1)参数向量θ 的加权递阶多新息最小二乘算法(weighted hierarchical multi-innovation least squares algorithm,W-HMILS算法):

2.3 遗忘因子递阶多新息最小二乘算法

在HMILS算法(47)～(55)中引入遗忘因子λ,便得到辨识系统(1)参数向量θ 的遗忘因子递阶多新息最小二乘算法(forgetting factor hierarchical multi-innovation least squares algorithm,FFHMILS算法):

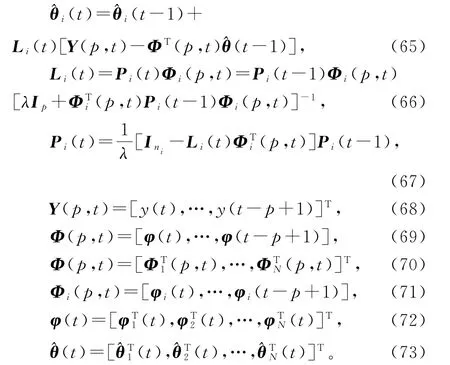
2.4 加权遗忘因子递阶多新息最小二乘算法

在HMILS算法(47)～(55)中引入加权因子wt和遗忘因子λ,便得到辨识系统(1)参数向量θ的加权遗忘因子递阶多新息最小二乘算法(weighted forgetting factor hierarchical multi-innovation least squares algorithm,W-FF-HMILS算法):

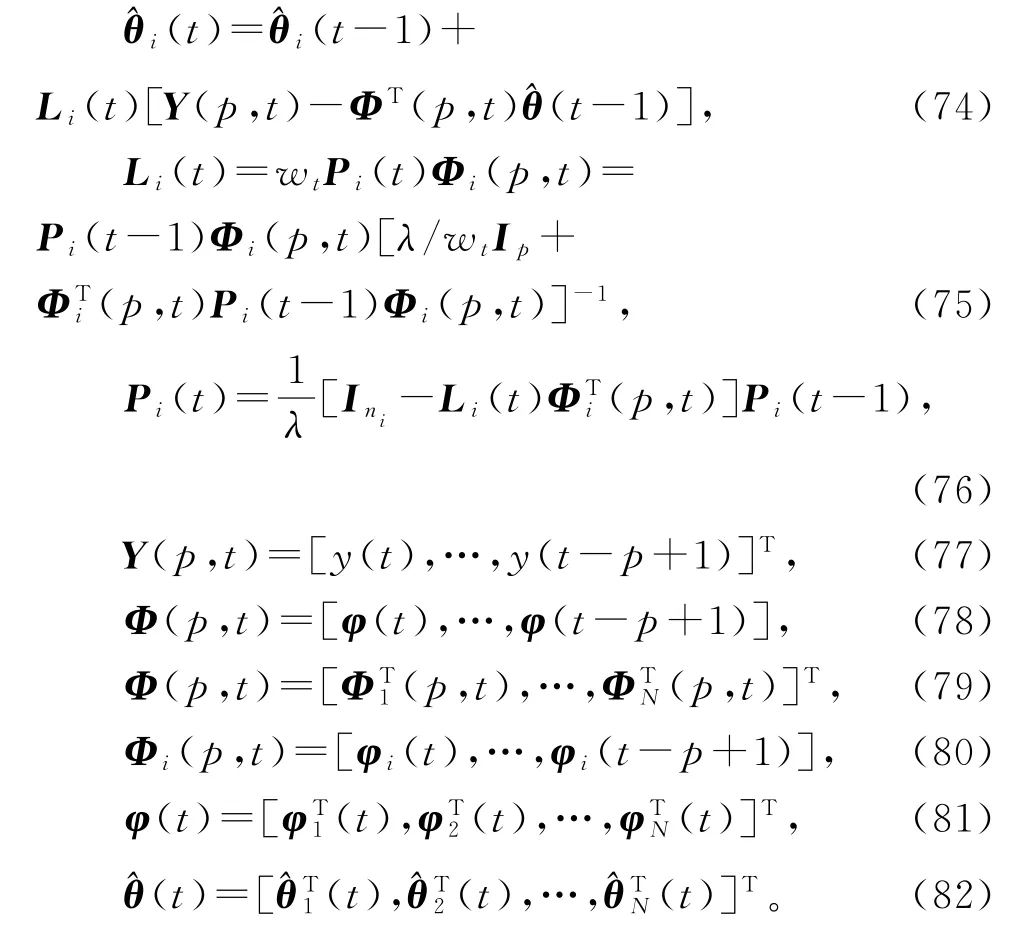
在W-FF-HMILS算法(74)～(82)中取遗忘因子λ＝1,就得到加权递阶多新息最小二乘(WHMILS)算法;取加权因子wt＝1,就得到遗忘因子递阶多新息最小二乘(FF-HMILS)算法。

3 递阶随机梯度辨识方法

考虑下列线性回归系统,

其中各变量的定义同上。将参数向量θ 分解为N 个维数为ni的子参数向量θi,将信息向量φ(t)分解为N 个维数为ni的子信息向量φi(t)如下:

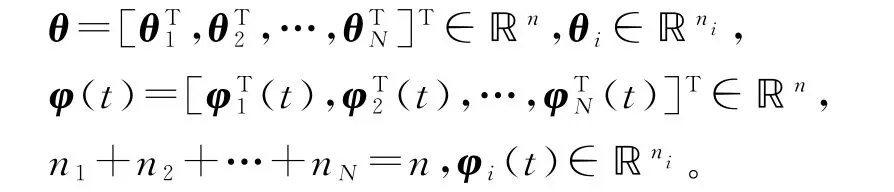
于是,可以把系统(83)分解为N 个虚拟子系统,即递阶辨识模型(H-ID模型):

yi(t)∈ℝ是虚拟子系统的输出,αi(t)∈ℝ称为各子系统间的关联项(associate item),它是通过参数θj(j≠i)耦合的。

3.1 随机梯度辨识方法

3.1.1 随机梯度辨识算法

对于线性回归辨识模型(83),定义梯度准则函数

极小化准则函数J3(θ),可以得到辨识线性回归系统(83)参数向量θ 的随机梯度算法(stochastic gradient algorithm,SG 算法)[5]:

3.1.2 加权随机梯度辨识算法

在SG 算法(87)～(89)中引入加权因子wt,可以得到辨识线性回归系统(83)参数向量θ 的加权随机梯度算法(weighted stochastic gradient algorithm,W-SG 算法):

3.1.3 遗忘因子随机梯度辨识算法

在SG 算法(87)～(89)中引入遗忘因子λ,就可以得到辨识线性回归系统(83)参数向量θ 的遗忘因子随机梯度算法(forgetting factor stochastic gradient algorithm,FFSG 算法):

3.1.4 加权遗忘因子随机梯度辨识算法

在SG 算法(87)～(89)中引入加权因子wt和遗忘因子λ,可以得到辨识线性回归系统(83)参数向量θ 的加权遗忘因子随机梯度算法(weighted forgetting factor stochastic gradient algorithm,WFFSG 算法):

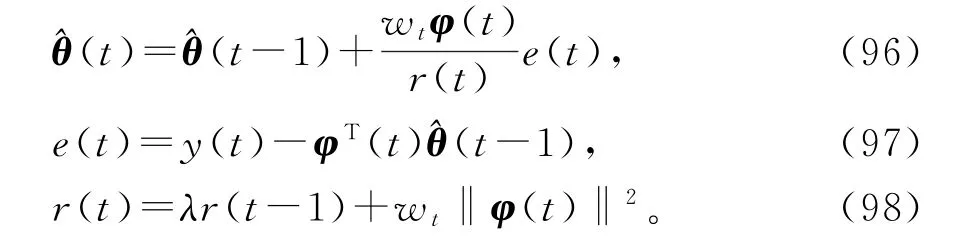
3.2 多新息随机梯度算法

为了改善SG 算法的收敛速度,利用多新息辨识理论[6],基于SG 辨识算法(87)～(89),引入新息长度p,将观测输出y(t)和信息向量φ(t)扩展为堆积输出向量Y(p,t)和堆积信息矩阵Φ(p,t):

将式(87)中标量新息(scalar innovation)e(t)∈ℝ扩展为新息向量(innovation vector),即多新息

可以得到辨识线性回归系统(83)参数向量θ的多新息随机梯度算法(multi-innovation stochastic gradient algorithm,MISG 算法):

当新息长度p＝1 时,MISG 辨识算法退化为SG 辨识算法(87)～(89)。

3.3 递阶随机梯度辨识算法

对于递阶辨识模型(84),定义关于子参数向量θi的梯度准则函数

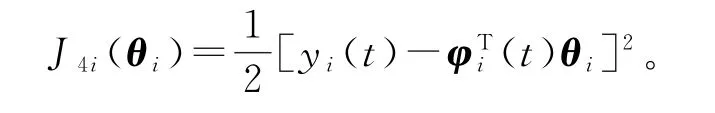
极小化准则函数J4i(θi),可以获得估计参数向量θi的梯度递推关系:

因为只有y(t)和φ(t)及其分量φi(t)是已知的,而虚拟子系统的输出yi(t)是未知的,故将式(85)中yi(t)代入式(105)得到

上式右边包含了其它子系统的未知子参数向量θj(j≠i),所以算法(106)～(107)无法实现。为了实现参数估计的递推计算,根据递阶辨识原理进行关联项的协调,式(107)中未知的θj用它在前一时刻(t－1)的估计(t－1)代替,可得

式(108)和式(106)构成了估计系统(83)参数向量θ 的递阶随机梯度算法(hierarchical stochastic gradient algorithm,HSG 算法):

如果式(109)中ri(t)用式(89)中的r(t)代替,那么HSG 算法(109)～(112)完全等同于随机梯度算法(87)～(89)。线性回归系统的递阶随机梯度类算法与随机梯度类算法的计算量没有大的差别,同样,线性回归系统的递阶梯度类算法与递推梯度类算法的计算量也没有大的差别。递阶辨识的优点主要体现在递阶最小二乘算法的计算效率上。

基于HSG 算法(109)～(112),在式(109)中引入收敛指数(convergence index,即

就得到修正递阶随机梯度算法(modified HSG algorithm,M-HSG 算法)。

基于HSG 算法(109)～(112),在式(110)中引入遗忘因子(forgetting factor)λ,即

就得到遗忘因子递阶随机梯度算法(forgetting factor HSG algorithm,FF-HSG 算法)。

基于HSG 算法(109)～(112),在式(109)中引入收敛指数(convergence index)ε,在式(110)中引入遗忘因子(forgetting factor)λ,即就得到遗忘因子修正递阶随机梯度算法(FF-MHSG 算法)。

4 递阶多新息随机梯度算法

众所周知,尽管随机梯度辨识算法的计算量小,但是收敛速度慢。为了提高随机梯度算法参数估计的收敛速度,本书作者首次提出了能提高参数估计精度的多新息辨识理论[6]。这里基于HSG 算法(109)～(112),引入新息长度(innovation length),将式(109)中标量新息(innovation)e(t)＝y(t)－扩展为新息向量(innovation vector)

整数p≥1 为新息长度。定义堆积输出向量(stacked output vector)Y(p,t),堆积信息矩阵(stacked information matrix)Φ(p,t)和堆积子信息矩阵Φi(p,t)如下:

联立式(117)～(121)和(110)～(112),就得到辨识线性回归系统(83)参数向量θ 的递阶多新息随机梯度算法(hierarchical multi-innovation stochastic gradient algorithm,HMISG 算法):

当新息长度p＝1时,HMISG算法退化为HSG 算法(109)～(112)。

基于HMISG 算法(122)～(130),在式(122)中引入收敛指数ε,即

就得到修正递阶多新息随机梯度算法(modified HMISG algorithm,M-HMISG 算法)。

基于HMISG 算法(122)～(130),在式(124)中引入遗忘因子λ,即

就得到遗忘因子递阶多新息随机梯度算法(forgetting factor HMISG algorithm,FF-HMISG 算法)。

基于HMISG 算法(122)～(130),在式(122)中引入收敛指数ε,在式(124)中引入遗忘因子λ,即

就得到遗忘因子修正递阶多新息随机梯度算法(FFM-HMISG 算法)。

5 递阶递推梯度辨识方法

5.1 递推梯度辨识算法

对于辨识模型(83),定义随时间t 递增的准则函数为

定义堆积输出信息向量Y(t)和堆积信息矩阵Φ(t)如下:

定义递推关系:

读者可以写出引入收敛指数、加权因子、遗忘因子后的修正递推梯度算法(M-RG 算法)、加权递推梯度算法(W-RG 算法)、遗忘因子递推梯度算法(FF-RG 算法)、加权修正递推梯度算法(W-M-RG算法)、遗忘因子修正递推梯度算法(FF-M-RG 算法)、加权遗忘因子修正递推梯度算法(W-FF-M-RG算法)。

5.2 多新息递推梯度算法

多新息辨识方法是考虑从t－p＋1到t的动态数据窗里的p 组数据作为一个整体推导出的辨识算法。对于辨识模型(83),定义堆积输出向量Y(p,t)和堆积信息矩阵Φ(p,t)如下:

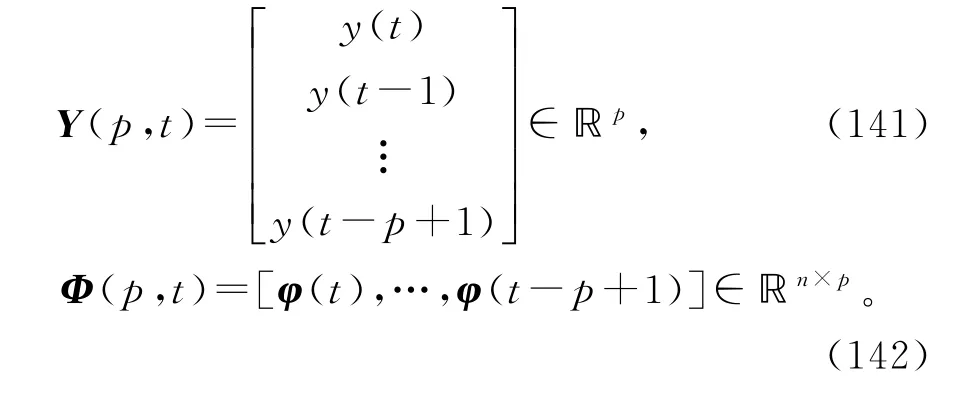
多新息梯度算法采用的随时间t递增的准则函数为

定义堆积输出信息向量Zt和堆积信息矩阵Ωt如下:

则准则函数J6(θ)可以写为

求准则函数J6(θ)对参数向量θ 的一阶偏导数,可以得到准则函数J6(θ)的梯度向量

在多新息梯度辨识算法(145)～(151)中引入收敛指数、加权因子、遗忘因子,便得到修正多新息梯度(M-MIG)算法、加权多新息梯度(W-MIG)算法、遗忘因子多新息梯度(FF-MIG)算法、加权修正多新息梯度(W-M-MIG)算法、遗忘因子修正多新息梯度(FF-M-MIG)算法、加权遗忘因子修正多新息梯度(W-FF-M-MIG)算法等。

多新息递推梯度类辨识方法是我们首次提出的。它可以发展为CARMA 模型的多新息增广梯度算法、CARAR 模型的多新息广义梯度算法、CARARMA 模型的多新息广义增广梯度算法,以及输出误差模型的辅助模型多新息梯度算法、OEMA模型的辅助模型多新息增广梯度算法、OEAR 模型的辅助模型多新息广义梯度算法、OEARMA 模型的辅助模型多新息广义增广梯度算法等。

5.3 递阶递推梯度辨识算法

这里介绍递阶递推梯度辨识方法,简称递阶梯度辨识方法。基于递阶辨识模型(84),定义N 个随时间t递增的准则函数:

定义堆积输出信息向量Y(t)和Yi(t),以及堆积信息矩阵Φ(t)和子信息矩阵Φi(t)如下:

使用负梯度搜索,极小化准则函数J7i(θi),仿照RG 辨识算法的推导,可得到基于梯度的递推关系:

由于式(156)右边包含了未知关联参数θj(j≠i),所以这个算法无法实现。为了解决这个问题,应用递阶辨识原理,用它们前一时刻的估计代替,得到式(160),联立式(154)～(155)和(157),便得到辨识系统(83)参数向量θ 的递阶递推梯度算法,简称递阶梯度算法(hierarchical gradient algorithm,HG 算法):

读者可以写出引入收敛指数、加权因子、遗忘因子后的修正递阶梯度(M-HG)算法、加权递阶梯度(W-HG)算法、遗忘因子递阶梯度(FF-HG)算法、加权修正递阶梯度(W-M-HG)算法、遗忘因子修正递阶梯度(FF-M-HG)算法、加权遗忘因子修正递阶梯度(W-FF-M-HG)算法。

6 递阶多新息梯度辨识算法

为简化,递阶递推辨识方法和多新息递推辨识方法中一般都省略“递推”二字,分别简称递阶辨识方法和多新息辨识方法,所以这里递阶多新息递推梯度辨识方法简称递阶多新息梯度辨识方法。

多新息辨识方法是考虑从t－p＋1到t的动态数据窗里的p 组数据作为一个整体推导出的辨识算法。对于递阶辨识模型(84),定义堆积输出向量Y(p,t)和Yi(p,t),堆积信息矩阵Φ(p,t)和子信息矩阵Φi(p,t)如下:

设μi(t)≥0为收敛因子。根据负梯度搜索,极小化准则函数J8i(θi),可得到下列梯度递推关系:

由于特征值计算很复杂,故收敛因子也可简单取为

由于式(167)右边包含了未知关联参数θj(j≠i),应用递阶辨识原理,用它们前一时刻的估计代替,得到

取μi(t)＝1/ri(t),ri(t)＝tr[Ri(t)]＝ri(t－1)＋‖φi(t)‖2,ri(0)＝1或ri(0)＝0时,联立式(169),(172),(168),(164)～(166),便得到辨识系统(83)参数向量θ 的递阶多新息递推梯度算法(hierarchical multi-innovation recursive gradient algorithm,HMIRG 算法):

读者可写出引入收敛指数、加权因子(加权矩阵)、遗忘因子后的修正递阶多新息梯度(MHMIG)算法、加权递阶多新息梯度(W-HMIG)算法、遗忘因子递阶多新息梯度(FF-HMIG)算法、加权修正递阶多新息梯度(W-M-HMIG)算法、遗忘因子修正递阶多新息梯度(FF-M-HMIG)算法、加权遗忘因子修正递阶多新息梯度(W-FF-M-HMIG)算法。

7 结 语

针对线性回归模型,利用系统的观测输入输出数据,基于递阶辨识原理,对辨识模型进行分解,得到系统的递阶辨识模型,推导出递阶(多新息)随机梯度算法、递阶(多新息)梯度算法、递阶(多新息)最小二乘算法等。递阶辨识原理能够用于参数多的大规模系统、结构复杂的非线性系统的辨识,目的是简化辨识方法和减小计算量。提出的分解辨识思想可以推广到大规模线性随机系统和复杂非线性随机系统的辨识,其干扰可以是有色噪声。