抗高过载MEMS器件双层异质防护结构的仿真研究*
冯登虎,石云波,赵 锐,陈玉楠,张 鹏,闫晓朋
(1.中北大学电子测试技术重点实验室,山西 太原 030051;2.山西北方机械制造有限责任公司,山西 太原 030000)
0 引 言
高过载冲击很容易对MEMS惯性器件内部[1~3]的机械结构造成影响,导致严重形变甚至断裂,从而使整个系统无法正常工作甚至失效[4~8]。因此,对MEMS 惯性器件进行有效的外部缓冲防护,以提高其稳定性和可靠性变得尤为重要[9]。外部缓冲防护[10]通过阻止过载冲击的传播途径,利用粘弹性材料的优越缓冲特性来大幅度提升MEMS 器件的抗高过载能力,有效地减少冲击传递到MEMS 器件的机械结构上的能量,并提供额外的支撑和固定,从而保护MEMS器件免受高过载环境的损害[11~13]。
Yoon S W等人[14]设计了一种软涂层结构,通过仿真发现可有效降低MEMS器件受到的40%的过载冲击。Wu J等人[15]研究了热冲击下环氧树脂和有机硅弹性体等涂层对MEMS器件的粘接强度;Li T T等人[16]提出了一种具有夹层结构的柔性聚氨酯泡沫复合材料,传感器测试结果与仿真数据表明,能量吸收水平较聚氨酯提升19%。进一步,石云波团队设计并分析了3 种基于粘弹性材料的高g值加速度传感器的灌封方法,在2 ×105gn冲击下测量精度最高可达5%[17]。
近年来,缓冲防护技术旨在论证说明粘弹性材料在缓冲吸能方面的有效性与可行性,而针对支撑其抗过载性能的防护与缓冲机理的研究,尤其是粘弹性材料的冲击动力响应特性研究较少。
本文围绕二阶振荡系统,探究高过载冲击中的力学参数变化规律,分析材料特性,基于高冲击加速度计设计仿真模型进行数值模拟,解决粘弹性材料理论与试验相脱节的问题,为高过载冲击下的粘弹性材料的抗高过载性能研究与应用提供了理论和技术支持。
1 双层异质结构动力学响应
1.1 粘弹性材料的线性化处理
典型的非线性粘弹性固体应力-应变曲线如图1 所示[18]。

图1 非线性粘弹性固体的典型应变-应力响应
显然,粘弹性材料本构曲线贴合双曲正切型材料规律[19],其本构模型为
考虑到双曲正切函数通解复杂,且难以获得其精确显示解,此处将其近似线性化分段处理,如图2 所示,对F-x曲线求曲率得到κ-x曲线,可发现,曲率极值点即为线性分段点。

图2 双曲正切型材料分段拟合
图2 中,κ代表双曲正切材料的曲率
式中μi,ηi为材料i在0~x1,x1~x2段斜率。
拉伸试验是一种材料力学测试方法,用于确定材料在拉伸负载下的机械性能。为获得聚氨酯、环氧树脂不同冲击载荷信号下的性能,对聚氨酯、环氧树脂进行拉伸性能测试,测试结果如图3。

图3 力学性能测试曲线
分别拟合聚氨酯/环氧树脂各阶段函数表达式,可得表1参数。

表1 材料参数
1.2 二阶振荡模型简化计算
由双曲正切材料建立的二阶振荡模型系统振动方程为
经图2 等效处理后二阶振荡模型系统振动方程如式(4)
根据二阶系统求解方法[20],内层、外层材料动态加速度响应为x″1,x″2,如式(5)
式中p1,p2,p3,p4和u1,u2,u3,u4分别为计算过程中实数部,则加速度峰值比同式(6)
2 数值计算
2.1 模型建立
通过对冲击应力波在防护结构中的传输和装置响应机理及系统的动力学分析,选用波阻抗不同的粘弹性材料聚氨酯和环氧树脂;模型包含底座、外部加速度传感器、系统外壳、双层粘弹性缓冲材料、内部加速度传感器等部分,结构剖面如图4。

图4 过载冲击试验双层缓冲防护试样结构
图4 中,L1和L2分别表示内外粘弹性材料层水平厚度,H1和H2分别表示应力传递方向上内外粘弹性材料厚度,定义L1/L2=H1/H2=r,为了准确评估不同厚度和界面层对缓冲性能的影响,设置如表2所示6组试验。

表2 不同厚度结构分类
2.2 不同厚度比数值计算
考虑到实际试验过程,以mm为单位建立模型,整体结构采用对称模型,建立拉格朗日正六面体网格[21],如图5。

图5 有限元计算网格
内外传感器均选用铝合金材料,模型采用Plastic_Kinematic,各材料参数如表1;聚氨酯和环氧树脂近似线性化处理,故材料模型采用Plastic_Kinematic;不同部件接触采用Automatic_Surface_to_Surface算法。给底座、外部传感器、壳体和顶盖加如图6 所示的半正弦惯性冲击载荷,缓冲防护材料相对夹具产生过载加速度。
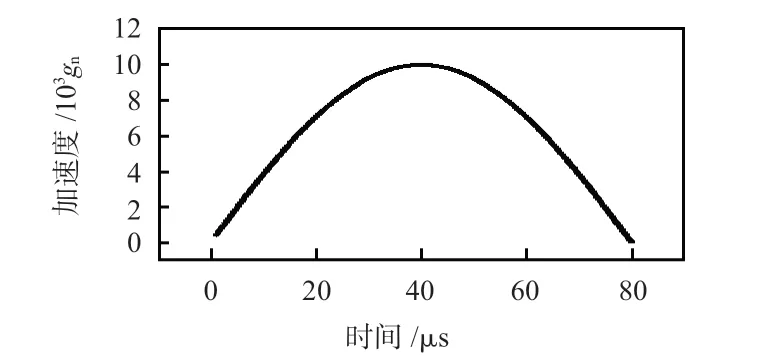
图6 冲击载荷加速度-时间曲线
2.3 仿真结果分析
采用表1 参数进行结构动力学仿真,分别对组一至组六进行数值仿真,组一和组四的仿真结果如图7所示。
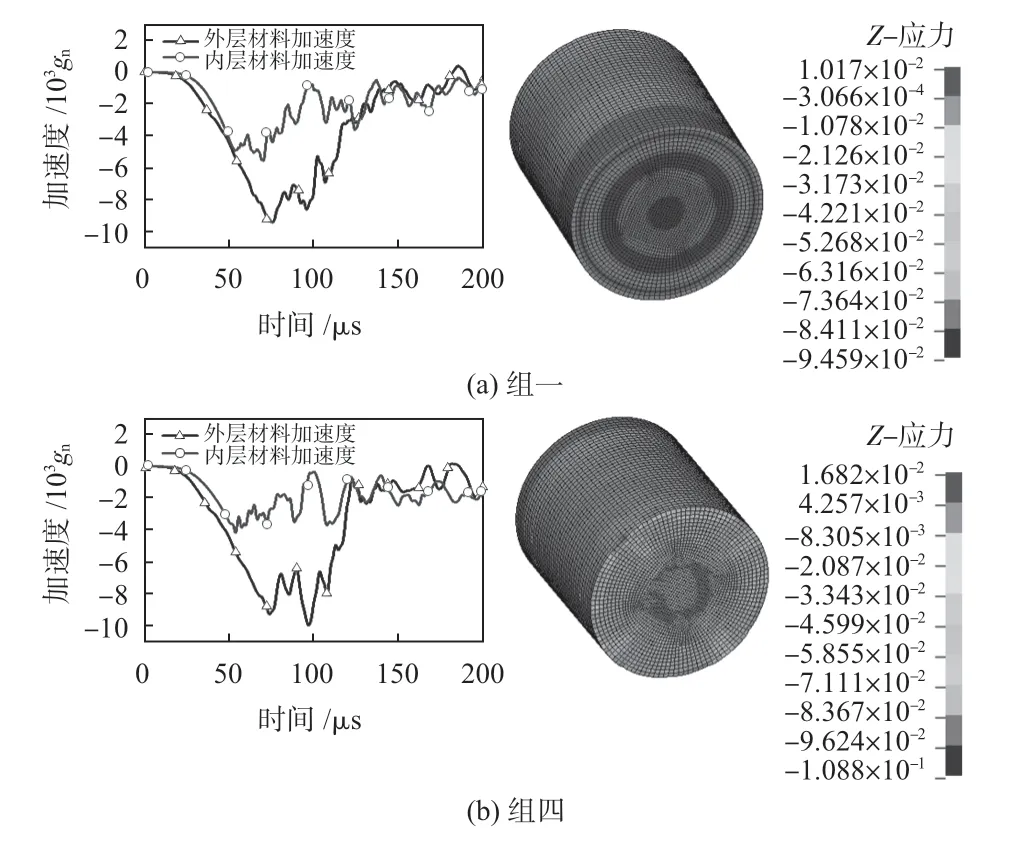
图7 组一和组四内外缓冲材料加速度对比及应力云图
图7 (a)为外层聚氨酯内层环氧树脂作为填充材料的加速度-时间历程仿真结果,输入加速度信号峰值为10 000gn,脉宽为80 μs;冲击载荷经底座传播,外部传感器于23.81 μs 开始响应,74.31 μs 时达加速度极值9 433gn,143.55 μs冲击响应过程结束,内部传感器由于冲击载荷经粘弹性材料传递,滞后外部传感器5.31 μs,于29.12 μs 时开始响应,68.37 μs时达峰值5629gn,之后由于输入过载的减小,129.43 μs时内部传感器恢复零位,由于内层缓冲材料的反复振动,过载波动降至零位。定义内外加速度峰值比为衰减比,则组一的衰减比为0.597。
图7(b)为外层聚氨酯内层环氧树脂作为填充材料的加速度-时间历程仿真结果,输入加速度信号与组一相同;外部传感器于23.74 μs 开始响应,97.33 μs 时达加速度极值9 471gn,124.35 μs冲击响应过程结束,内部传感器由于冲击载荷经粘弹性材料传递,滞后外部传感器5.12 μs,于28.86 μs时开始响应,54.21 μs时达峰值4 489gn,96.33 μs时内部传感器恢复零位,过载波动降至零位。组四的衰减比为0.47。
同理,将6组数据汇总,可得如表3仿真结果。

表3 仿真与理论计算结果
对比同结构不同组,外层环氧树脂内层聚氨酯结构的衰减比明显小于同结构的外层聚氨酯内层环氧树脂结构,衰减比最低为0.47,衰减比随厚度比的减小增大,理论与仿真的误差均在4.60%以内。
3 结 论
本文针对MEMS惯性器件的防护结构,采用分段拟合法建立粘弹性材料本构模型,结合二阶振荡系统的动力学分析理论,获得不同厚度比双层异质结构的加速度响应过程。通过理论计算和动力学数值仿真,结果表明:组四(内层聚氨酯外层环氧树脂厚度比为2∶1)的响应加速度峰值比最低可至0.47,较同厚度比下的组一提升20.80%。本文有效验证了双层异质防护结构不同厚度下的缓冲吸能性能,为进一步提升防护结构的抗高过载性能,双层防护结构下缓冲材料的设计参数,仍待今后不断深入研究。

