全金属固态振动陀螺振子特性仿真分析*

周建欣，刘 洪，谢 帅，祝正原，于东明

（北京信息科技大学高动态导航技术北京市重点实验室，北京 100101）

0 引 言

现有的半球陀螺仪、光纤陀螺仪，均无法适应极端瞬态力作用；微机电系统（MEMS）陀螺仪体积小，但测量精度不高；压电金属振动陀螺仪抗高过载性能强，但体积缩小受限，难以满足被测体高精度姿态测量和导航需求。因此，迫切需要研制一种同时具备小体积、抗高过载、高性能、低成本等特点的新型陀螺。

本文为解决高过载环境下小体积载体姿态测量的问题，设计了一种新型的全金属固态振动陀螺（all-metal solidstate vibrating gyro，ASVG）。ASVG是一种目前可以广泛用于精确测量各种载体振动角度和速率的装置［1］。对于谐振陀螺，核心部件振子的振型稳定、抗干扰能力及灵敏度取决于振子的固有频率和振幅是否合理［2］。综上，本文在ASVG振子的设计上，通过模态分析计算出振子的固有频率及振型，以便准确设置激励信号的频率，并且通过谐响应分析计算振子在静电力作用下的位移响应。为了保证振子在承受极端瞬态力的过程中不发生不可自行恢复的变形，通过受力仿真分析，分析振子壳体结构在不同过载下的受力情况。

1 ASVG工作原理

ASVG基于科里奥利效应，利用振子表面的驻波进动效应来测量载体的角速率。采用金属材料制成的轴对称振子作为核心结构，当载体存在角运动时，在科里奥利力作用下，振型相对于外壳体产生环向进动［3］。

ASVG核心部件主要由金属半球壳振子、平面电极底座两部分组成。振子结构如图1（b）、图1（c）所示，主要结构为半球壳体，结构均匀轴对称，支撑杆和半球壳衔接部位有过渡圆角，支撑杆下端的小柱固定到底座，振子端面与平面电极之间形成微小间隙。振子封装在金属罩中并且抽真空，陀螺的激励电极与检测电极在同一平面，电极间进行信号屏蔽设计，均匀分布，如图1（c）所示。在激励电极1、电极5和施加交流电压，在静电力的作用下，振子振动于激励模态，由图1（c）检测电极3 和电极7 检测，模态方向和激励电极方向相同。检测模态在振子产生一个逆时针旋转方向的角速度时，由于科里奥利效应产生，利用反馈电极2 和电极6检测这个模态，通过控制电极4 和电极8 抑制检测模态的振动，激励模态和检测同时作用于振子上，如图2 所示，使振型偏转［4］。因为用来抑制振子振动的电压幅值和角速度成正比，经过解算，最终得到角速率。

图1 ASVG振子结构与电极分布

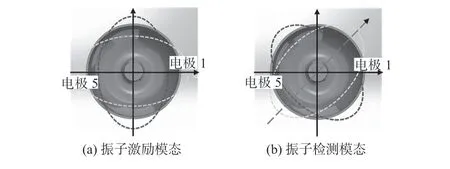
图2 ASVG振子振动模态

2 振子模态仿真分析

2.1 结构材料约束

本文采用有限元分析软件进行模态仿真，分析振子的振动特性，模态是结构的固有振动特性，每一个模态都有对应的固有频率和振型［5，6］。在模态仿真分析中，振子的材料特性也影响结构本身的振动特性［7］。振子选用金属材料，具备承受更大过载冲击的能力。要根据振子的结构特点和性能要求选用具备高Q值、均匀的密度、弹性模量及泊松比等特点的材料［8］。通过振子结构设计及材料特性研究已知，材料密度越大，振子固有频率越小；弹性模量越大，振子固有频率越大；泊松比越大，振子固有频率越大。以上因素对振子固有频率的影响情况不同，泊松比影响最大，其次是杨氏模量、密度。

振子结构选用3J33，品质因数为20 000，线性膨胀系数为3.5 ×10-6／℃，弹性模量为170 ～210 GPa，材料密度为8.0 g／cm3，泊松比为0.3，杨氏模量温度系数为16 ×10-6～13 ×10-6／℃，屈服强度为450 MPa。3J33 线性膨胀系数较低，材料温度性能较好，符合陀螺大范围温度工作。并且3J33易于加工，具备高强度、高韧性等特点，抗腐蚀性能与裂纹扩展能力较强，提高器件的寿命。

2.2 振子模型建立及仿真

设置振子结构内半径、外半径、壁厚、支撑柱伸出球壳边缘柱长度、支撑柱直径、固定杆直径、固定杆长度及内圆角半径参数分别为：4.8，5.0，0.2，3.005，2.0，1.0，1.505，1.0 mm。

通过有限元分析软件，导入振子三维结构［9］，设置0.1 mm网格精细划分，约束振子固定接触面，通过仿真计算，得到1阶～6阶模态的固有频率和振型，如图3和表1所示。

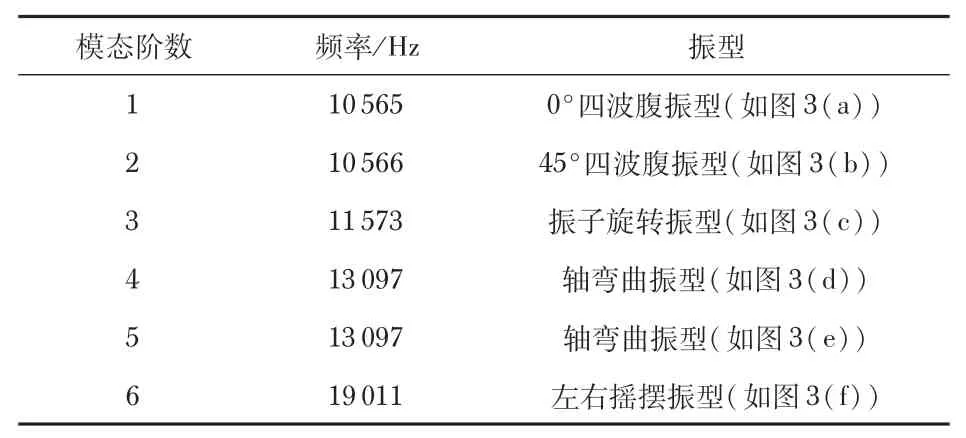
表1 振子模态仿真结果

图3 ASVG振子模态分析振型

振子1 阶、2 阶振型为四波腹振型，2 阶振型与1 阶振型相差45°，即为振子工作模态，3 阶振型为旋转振型，4 阶～6 阶振型为左右摇摆振型，振子模态隔离度为1 007.0 Hz。

3 振子谐响应分析

在振子的0°方向的半球壳唇沿上施加大小为0.1 N的力，得到振子最大位移与频率的关系［10，11］，如图4（a）所示，当频率值为10 565.3 Hz时，振子位移值最大，此时振子振型对应振子的1 阶模态振型，振动幅值为3.032 μm，可以作为振子的驱动模态。在振子的45°方向的半球壳唇沿上施加大小为0.1 N 的力，得到振子表面最大位移与频率的关系，如图4（b）所示，当频率值为10565.7 Hz时，振子位移值最大，此时振子振型对应振子的2阶模态振型，振动幅值为10.760 μm，作为陀螺的检测模态。

4 振子过载特性分析

本文在进行ASVG振子过载特性分析时，利用有限元分析软件，建立有限元模型，采用静态法，约束振子固定位置，在纵轴向施加不同过载冲击值，并分析振子结构受力情况，结果如图5所示。得到振子在施加不同冲击力时振子的应力值及位移变化，结果如表2所示，理论上振子可以承受16 ×104gn及以下的过载冲击，在此范围内振子不会发生塑性形变，最大应力值远小于3J33 材料的屈服强度450 MPa，满足振子抗高过载性能要求［12］。

表2 振子过载仿真结果

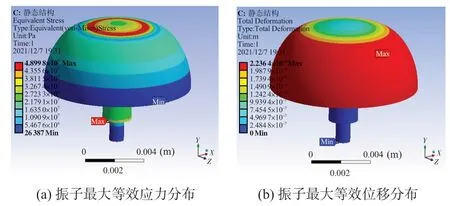
图5 ASVG振子过载分析

5 实验测试

在实验室大气环境下，环境温度为20～30 ℃，相对湿度为20%～80%RH，将振子安装在测试工作台上的夹具中，通过频率特性分析仪，设置交流电压信号源，给振子施加激励信号，采用Polytec 激光测振仪采集振子振动信号。测试系统如图6所示。

根据实验测试结果，振子在激励频率为11 065.30 Hz时产生四波腹振动，如图7所示。

图7 振子四波腹振型

由于加工精度与材料参数导致实测数据与仿真数据不同。经仿真计算，壁厚增加0.1 mm，直径10 mm 振子固有频率程线性增加约900 Hz；在材料密度变化范围内，振子固有频率变化50 Hz，在弹性模量变化范围内，振子固有频率变化1 144 Hz，在泊松比变化范围内，振子固有频率变化-88 Hz，因此，振子固有频率误差在仿真范围内，此结构具备振子特性，证明本文仿真方法的准确性。

6 结 论

本文对直径为10 mm的ASVG振子进行了特性仿真分析。通过模态分析及谐响应分析，得到振子的固有频率及各模态振型，振子在特定载荷下的振动情况。振子的驱动模态振动频率为10565 Hz，检测模态振动频率为10566 Hz，振子工作模态频率与下一阶模态频率相差大于1 000 Hz。对振子进行过载特性仿真分析，得出振子在不同过载下的最大应力值及最大位移值，振子最大可承受16 ×104gn以下的过载冲击，最大应力值为408.36 MPa，最大位移值为17.89 μm。从两方面分析得出现有振子结构满足陀螺工作原理，并加工出结构进行测试，验证了仿真方法的准确性。