自适应卡尔曼滤波在航空重力异常解算的应用研究

郑崴， 张贵宾

1 中国地质大学(北京)地球物理与信息技术学院， 北京　100083 2 河南科技学院信息工程学院， 河南新乡　453003

自适应卡尔曼滤波在航空重力异常解算的应用研究

郑崴1,2， 张贵宾1*

1 中国地质大学(北京)地球物理与信息技术学院， 北京100083 2 河南科技学院信息工程学院， 河南新乡453003

摘要依据航空重力测量基本原理，构建了航空重力异常解算的卡尔曼滤波模型，将新息自适应卡尔曼滤波器(IAE，Innovation based Adaptive Estimation)应用于量测噪声未知的航空重力异常解算.针对IAE滤波器滑动窗口宽度难以准确确定的问题，通过对多个不同滑动窗口新息协方差估计的加权平均，获得改进的IAE滤波器，该IAE滤波器不仅具有量测噪声自适应估计能力，还能实现滑动采样窗口的优化选取.试验结果表明，IAE滤波器可以降低因量测噪声统计信息不明引起的解算误差，改进IAE解算的重力异常误差约为1 mGal.

关键词航空重力异常解算； 自适应卡尔曼滤波； 新息； 量测噪声

1引言

航空重力测量是以飞机为载体，测量近地空中重力异常的重力测量技术，它综合运用了航空重力仪，全球定位系统GPS(Global Position System)，惯性导航系统INS(Inertial Navigation System)，无线电等技术设备(张昌达，2005；熊盛青，2009a；王静波等，2009，2010).航空重力测量数据经过后处理，便可得到所需的航空重力异常，这个数据后处理的过程称为航空重力异常解算(简称为航重解算).近年来，差分GPS技术的进步使得航空重力测量精度大幅度提高，解算所得重力异常精度大部分可达到1～2 mGal(1 mGal=10-5m·s-2)，最高的已达0.5 mGal(郭志宏等，2008；熊盛青，2009b; 熊盛青等，2010；Cai et al.，2013).

航空重力测量是在高速飞行运动中进行的，测量数据必然会受到包括飞机运动产生的扰动加速度的干扰，干扰噪声的幅度最高可达到106mGal以上(孙中苗，2004)，远远高于几十到几百毫伽的重力异常信号.航空重力测量数据的噪声主要体现为高频干扰，依据测量数据的频域特点设计低通滤波器可消除噪声影响提取所需的重力异常信号.目前，能够实现线性相位的FIR(Finite Impulse Response)滤波器是航重解算普遍采用的低通滤波器，利用FIR低通滤波器可以获得精度约1 mGal左右的航空重力异常(郭志宏等，2007, 2011).FIR滤波器的显著优点是具有成熟的设计和实现方法，但由于重力信号与噪声在频谱上没有明显的分界线，为获得高精度的解算输出，需设计高阶的低通滤波器以分离重力异常信号与噪声(蔡劭琨等，2010；Cai et al.，2010；罗峰等，2012)，这加重了边界效应对解算结果的影响.

部分学者致力于利用卡尔曼滤波器代替数字低通滤波器实现航空重力异常的解算(Bolotin et al.，2003；Bolotin and Popelensky，2007；Bolotin and Golovan，2013).卡尔曼滤波器通常是采用状态空间模型在时间域对系统的运动状态进行描述，因此卡尔曼滤波器是基于系统运动模型的滤波方法.状态空间模型的应用将不可观测的变量(状态变量)并入可观测的模型，并与其一起处理得到相应的估计输出，所以卡尔曼滤波可实现多维信号的并行处理(王静波，2010；王静波等，2011).在进行航重解算时，还能够对航空重力仪校准参数进行实时估计(Zhou and Cai，2013；Zheng et al.，2014).此外，航重解算是在线下进行的，可对卡尔曼滤波的估计结果进行平滑处理，获得高精度的航空重力异常输出(潘炎冰，2012；李瑞，2014).但是，卡尔曼滤波能够获得准确解算输出的重要前提，是能够掌握系统噪声和量测噪声的统计信息，而这一前提往往是难以满足的.解决这一问题的办法就是用自适应卡尔曼滤波器(AKF, Adaptive Kalman filter)代替传统的标准卡尔曼滤波器(SK, Standard Kalman filter)进行航重解算.基于新息协方差估计的自适应卡尔曼滤波器(IAE, Innovation-based Adaptive Estimation)已证明可以提高噪声统计特性不明时的估计精度(Mohamed，1999；Mohamed and Schwarz，1999)，IAE的优点在于实现方法简单且能够对量测噪声协方差进行实时估计，但其新息协方差估计器的滑动采样窗口宽度缺乏明确的确定方法.

航重解算中，卡尔曼滤波所需的量测量由GPS测定的位置或速度数据提供.由于测量过程中飞机运动状态变化剧烈且具有不规律性，量测噪声参数难以准确预设，因此这里着重讨论利用IAE滤波器实现量测噪声自适应的航重解算方法.本文将依据航空重力测量的基本原理，建立航空重力异常解算的卡尔曼滤波模型，设计适用于G型航空重力测量系统的IAE滤波器.另外，针对IAE滤波器的滑动窗口宽度难以准确确定的问题，采用多个不同滑动窗口宽度的新息协方差估计器，通过对多个新息协方差估计的加权平均，获得滑动窗口宽度优化的改进IAE滤波器.最后，将IAE滤波器和改进的IAE滤波器用于实测数据的航重解算试验.

2新息自适应卡尔曼滤波器及改进

2.1新息自适应卡尔曼滤波器

设在时刻k，离散线性系统的状态方程和量测方程可分别表示为

(1)

(2)

Xk为k时刻的状态变量；Φk,k-1表示由k-1时刻到k时刻的一步转移矩阵；Γk-1为系统噪声驱动阵；Zk为时刻k的量测量；Hk为量测阵；Wk-1为系统激励噪声序列；Vk为量测噪声序列.Qk是系统噪声的协方差阵；Rk为量测噪声协方差阵，则标准卡尔曼滤波的算法为(秦永元等，2012)

状态一步预测：

(3)

一步预测误差：

(4)

滤波增益：

(5)

状态估计：

(6)

估计均方误差：

(7)

新息(Innovation)定义为k时刻滤波器的量测估计值与实际量测值之差，它表示由量测量带来的、滤波器无法预测的那部分信息，即

(8)

新息序列的理论协方差为Crk，则有

(9)

当系统噪声和量测噪声服从不相关的高斯分布且新息序列满足各态遍历性时，可根据新息序列的滑动平均获得新息协方差的极大似然估计，有(MohamedandSchwarz，1999；岳晓奎和袁建平，2005；卞鸿巍等，2006)

(10)

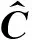
(11)

则量测噪声协方差阵的自适应估计为

(12)

2.2滑动采样窗口宽度的优化

实际应用中，如建立的系统模型不准确，不能真实反映物理过程时，易导致模型与获得的量测值不匹配，将会出现滤波发散，这时需通过增大当前时刻量测信息在状态估计中的加权系数来抑制滤波发散(秦永元等，2012).

图1　滑动采样窗口优化Fig.1　Structure of optimization for sliding sampling window

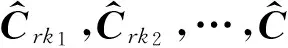
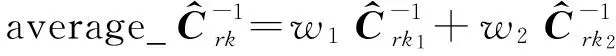
(13)

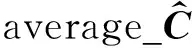
(14)

(15)

可见，相比于普通的IAE滤波器，改进的IAE滤波器配备有多个不同滑动采样窗口宽度的新息协方差估计器，通过对不同采样窗口的新息协方差估计进行加权平均，允许新息协方差估计器的滑动采样窗口在一定范围内动态变化，一方面可以减弱不当的滑动采样窗口造成的解算误差，另一方面也可以提高滤波器工作的稳定性，其估计精度劣于取最优滑动采样窗口的情况，但优于其他滑动采样窗口宽度的估计结果.多个新息方差估计器的结构如图1所示.

2.3 RTS(Rauch-Tung-Striebel)平滑器

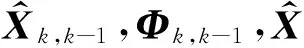
(16)

(17)

(18)

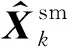
3航空重力异常解算的卡尔曼滤波模型

G型航空重力测量系统是三轴稳定平台型测量系统，它包括一个具有水平稳定作用的惯性平台(INS)，一个重力传感器(航空重力仪)，以及机载GPS接收器(移动站)和地面GPS接收器(接收站).本部分将根据航空重力仪运动方程及GPS测量方程构建航重解算的卡尔曼滤波模型.

3.1航空重力测量的基本原理

航空重力测量的基本原理是从航空重力仪测得的比力数据(飞机运动加速度与重力加速度之和)中扣除飞机运动加速度的影响，获得所需要的重力加速度(熊盛青等，2010).根据牛顿第二定律，航空重力仪(垂直加速度计)传感器探测质量(SM，Sensitive Mass)在地理垂直方向上的动力学方程可表示为(Bolotin，2009)

(19)

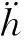
厄特缶斯改正是为了补偿因地球自转产生的离心力和飞机运动产生的离心力附加在重力仪测量质点造成的测量误差，可计算为

(20)

uE为地球自转速度；φ为飞机所处地理纬度；vE、vN分别是飞机的东向速度和北向速度；RE、RN分别是地理东向和北向的曲率半径.

重力正常场和高度改正项G0(φ,h)可由Helmert公式近似计算(Bolotin，2009)：

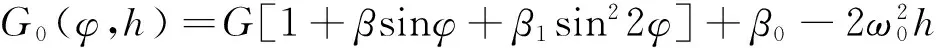
(21)

式中，G=9.7803 m·s-2，β=0.005302，

β1=-0.000007，β0=-0.00014 m·s-2，

ω0=0.00123 s-1.

不难看出，为获得式(19)中的重力异常Δg，需要对航空重力仪测量数据进行一系列的改正.其中，一部分改正项有严密的解析公式，可以直接计算得到，如厄特缶斯改正、正常场和高度改正，它们统称为解析类改正；而另一类改正无法直接用解析公式来计算，需借助滤波方法来实现，即垂直加速度改正.因此，利用卡尔曼滤波实现重力异常解算实际上是在消除噪声干扰的同时实现垂直加速度改正的过程.3.2卡尔曼滤波模型的建立

将航空重力仪SM的实时高程，作为卡尔曼滤波的量测方程，写为

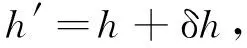
(22)

h′为重力仪SM所处的实时高度；h为SM的实际高度；δh为测量误差.

航空重力仪及两个水平加速度计的测量方程可表示为(Bolotin，2009)

(23)

将式(23)代入式(19)联立并整理得

(24)

其中

(25)

fΣ为已知的作用在SM上的合力产生的加速度总和；qΣ为系统噪声项.为实现航重解算，将重力异常看作沿测线分布的随机过程，并用滤波器表示，有

(26)

将式(24)和式(26)合并作为卡尔曼滤波的系统方程，式(22)为卡尔曼滤波的量测方程，并用状态空间形式表示为

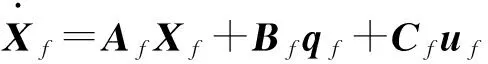
(27)

(28)

其中，Xf为状态向量，重力异常Δg为其分量，即

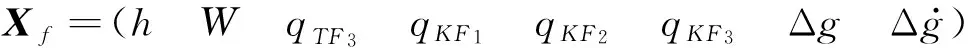
(29)

Af为动力学矩阵；Bf为系统噪声驱动矩阵；Cf为控制项驱动矩阵；qf和δh分别为系统噪声和量测噪声项；uf为系统的固定控制项.将式(27)和(28)进行离散化，再利用设计的IAE滤波器和RTS平滑器进行处理，即可实现重力异常的估计.

4航空重力异常解算试验

4.1测量基本情况

我们在2007年利用G型航空重力测量系统在某地进行了实地测量.实验所用数据为第五架次飞行测量数据，飞行时间为4 h.此次测量是为了验证系统工作的稳定性及重复测量结果的一致性.图2为测线位置示意图，图中横轴为相对经度，纵轴为相对纬度.由图可知，此次测量共有6条东西方向的飞行测线，其中1号、2号、3号及6号测线为四条短测线，它们是沿同一位置往返飞行4次的重复测线；4号测线和5号测线为两条长飞行测线，其中5号测线相较其他测线有约0.002°的北向偏移.测量选取在气象条件较好的夜间进行，以减小气流对测量结果的影响.测量中，设计飞行高度为400 m，实际飞行测量高度在设计飞行高度的±15 m范围内波动，图3为飞行测量高度变化示意图.此外，飞行测量中的设计飞行速度为60 m·s-1.

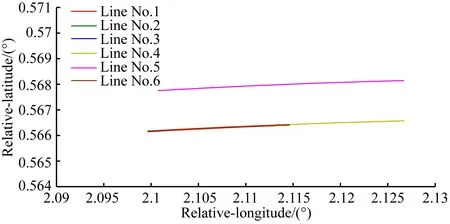
图2　测线位置示意图Fig.2　Position diagram of survey lines

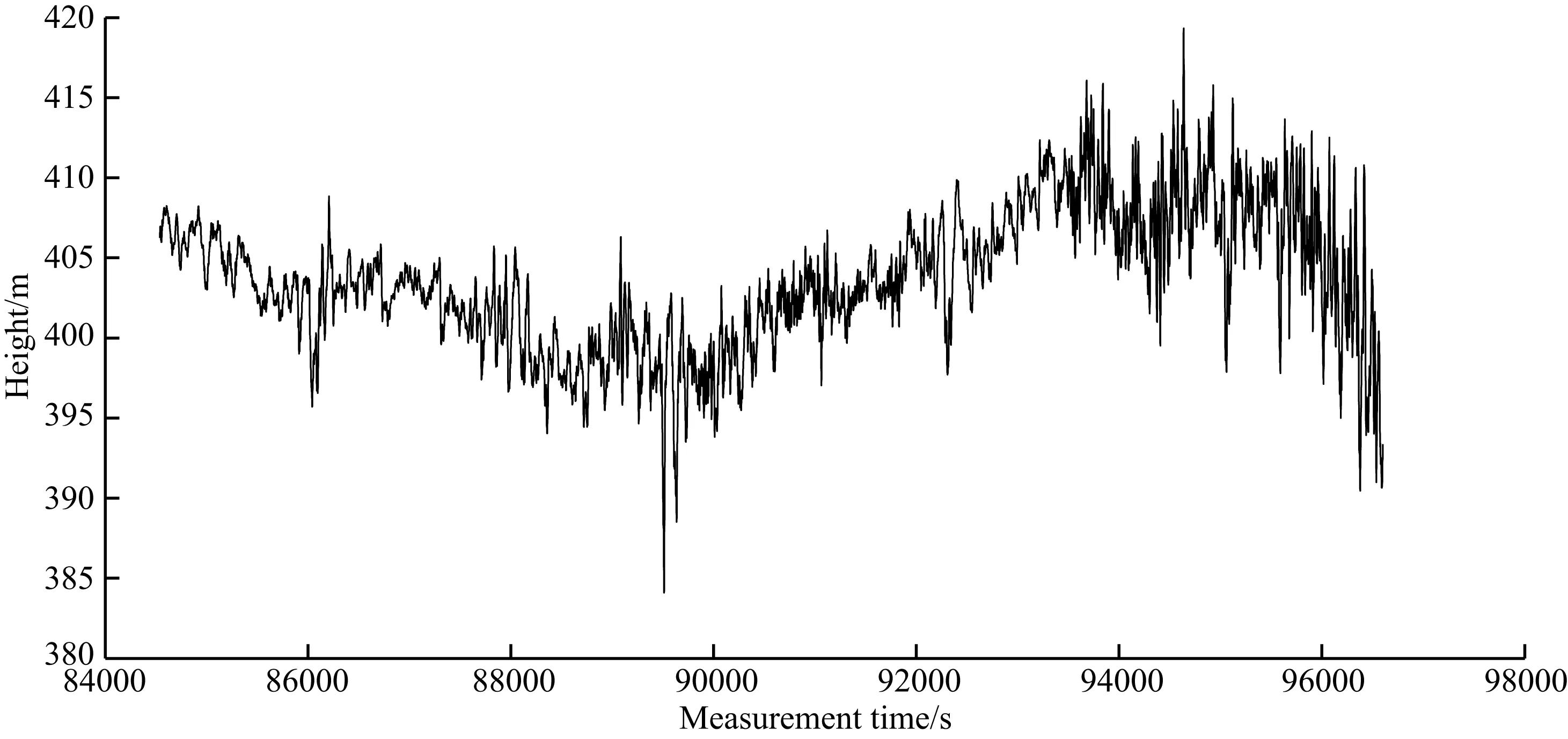
图3　飞行高度示意图Fig.3　Chart of flight height

剔除实测数据中的非测线数据，并进行解析类改正后，所得结果(未滤波)如图4所示.不难看出，航空重力测量信号受噪声干扰非常严重，几十到几百毫伽的重力异常完全被数万毫伽的噪声所淹没.

关于解算试验有以下两点需要说明，第一，由于暂无法获得实际地面重力测量数据，试验过程中将航空重力测量系统配套软件解算结果作为解算参考标准，将本试验的解算结果与参考标准进行对比研究；第二，由于RTS平滑后的重力异常精度高于只使用卡尔曼滤波器估计的重力异常精度(潘炎冰，2012；李瑞，2014)，因此后文解算结果如无特别说明均是指平滑处理后的重力异常.

4.2不同预设量测噪声的航空重力异常解算试验

将SK解算的重力异常与参考标准进行对比，通过反复调整量测噪声和系统噪声，获得与解算参考标准误差最小时的量测噪声和系统噪声分别为R0=(0.0153)2和Q0=diag[0,(3.5×10-5)2,0,0,0,0,0,(0.85×10-7)2]，diag[·]为取对角线元素符号.实验中SK和IAE的系统噪声设定为Q0，初始量测噪声R分别预设为R/R0=0.01、0.25、25、100进行解算.同时，为确保新息协方差估计的准确性，IAE的滑动采样窗口宽度暂设为80.

SK和IAE在不同预设量测噪声时，解算的重力异常如图5所示.为方便分析，将解算所得6条飞行测线的重力异常按时间顺序连接组成一条曲线，红色曲线为解算参考标准，蓝色曲线为SK解算的重力异常曲线，黑色曲线为IAE解算的重力异常曲线.由图可见，SK解算的重力异常曲线随着预设R的变化出现较大的波动，而且预设的R与R0的偏差越大，SK解算重力异常的误差也越高；而在同样的量测噪声条件下，IAE解算的重力异常曲线基本保持稳定，即IAE可降低因预设量测噪声不当引起的解算误差.

统计SK和IAE解算输出与参考标准的误差，如表1所示.可以看到，在预设量测噪声R=0.01R0时，SK解算结果的均方误差高达3.423367mGal；当预设量测噪声R=0.25R0时，SK解算重力异常与参考标准的均方误差为1.198765mGal.在IAE解算误差一栏中，不同预设量测噪声条件下，IAE解算重力异常的最大均方误差为0.923542mGal，最小均方误差为0.887827mGal，两者的差距仅为0.035715mGal，而且IAE解算结果与解算参考标准的误差都保持在1 mGal以下.所以，IAE滤波器在解算过程中对量测噪声协方差进行实时的估计和修正，减弱了解算精度对先验量测噪声统计信息的依赖.因此，相比基于SK的航重解算方法，利用IAE进行航重解算更具有普遍性的意义.

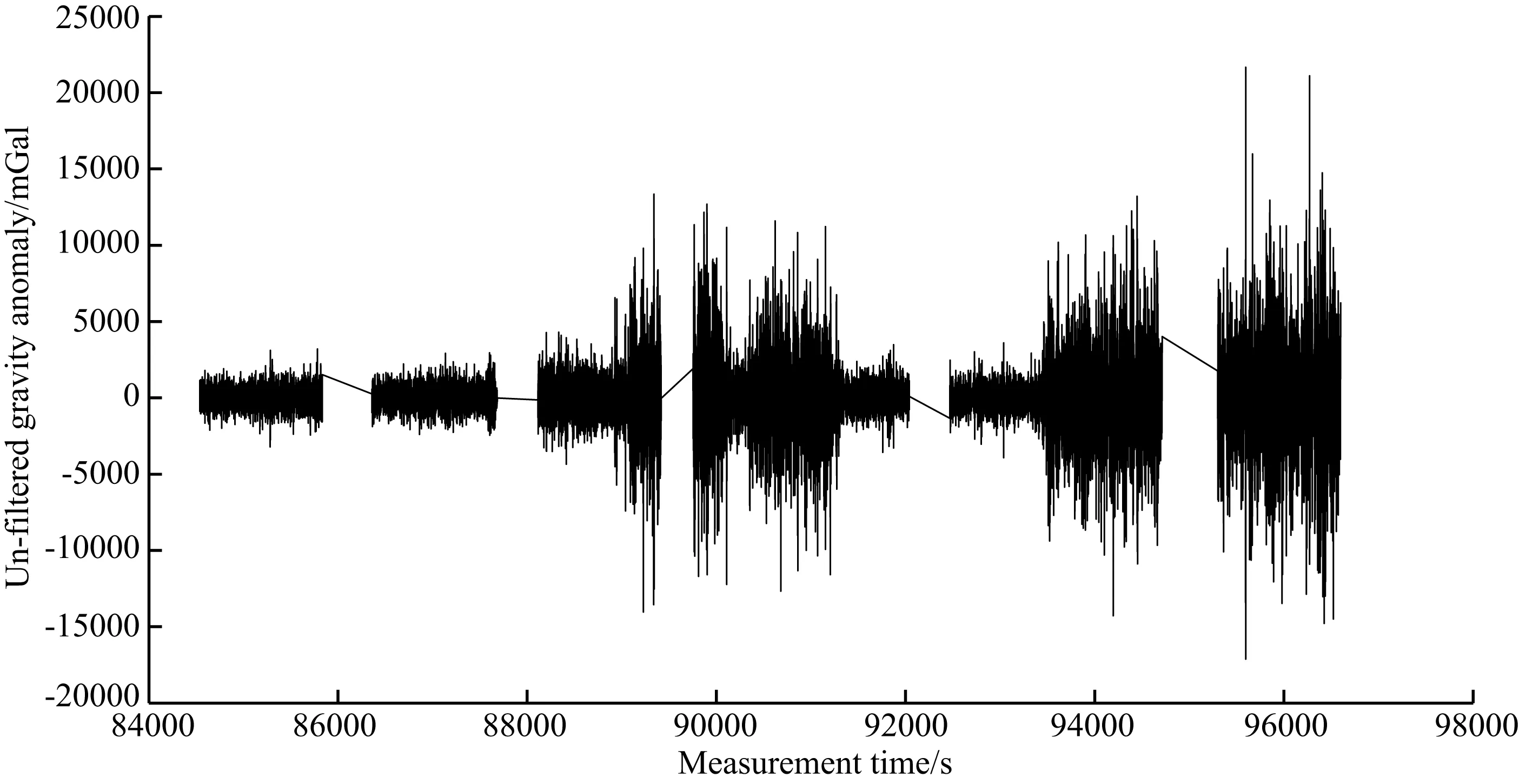
图4　未滤波航空重力异常Fig.4　Un-filtered airborne gravity anomaly

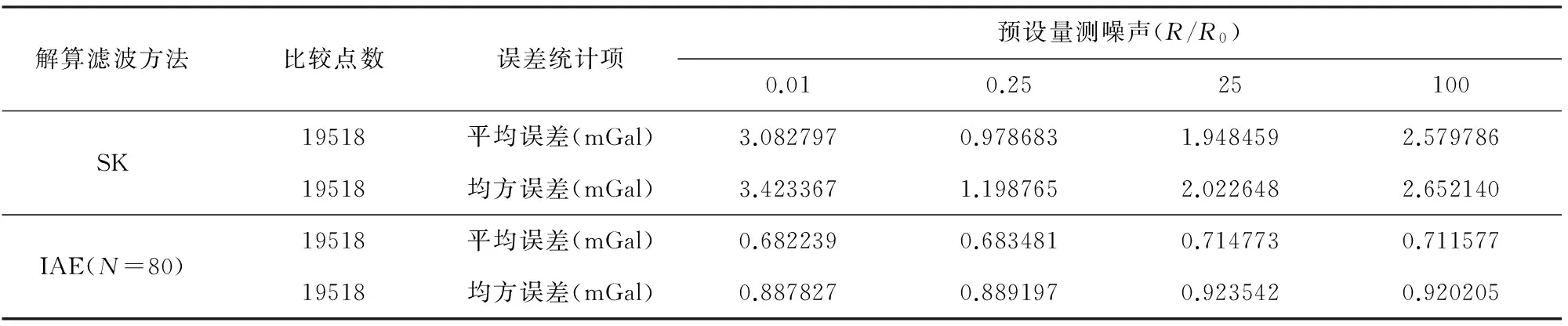
解算滤波方法比较点数误差统计项预设量测噪声(R/R0)0.010.2525100SK19518平均误差(mGal)3.0827970.9786831.9484592.57978619518均方误差(mGal)3.4233671.1987652.0226482.652140IAE(N=80)19518平均误差(mGal)0.6822390.6834810.7147730.71157719518均方误差(mGal)0.8878270.8891970.9235420.920205

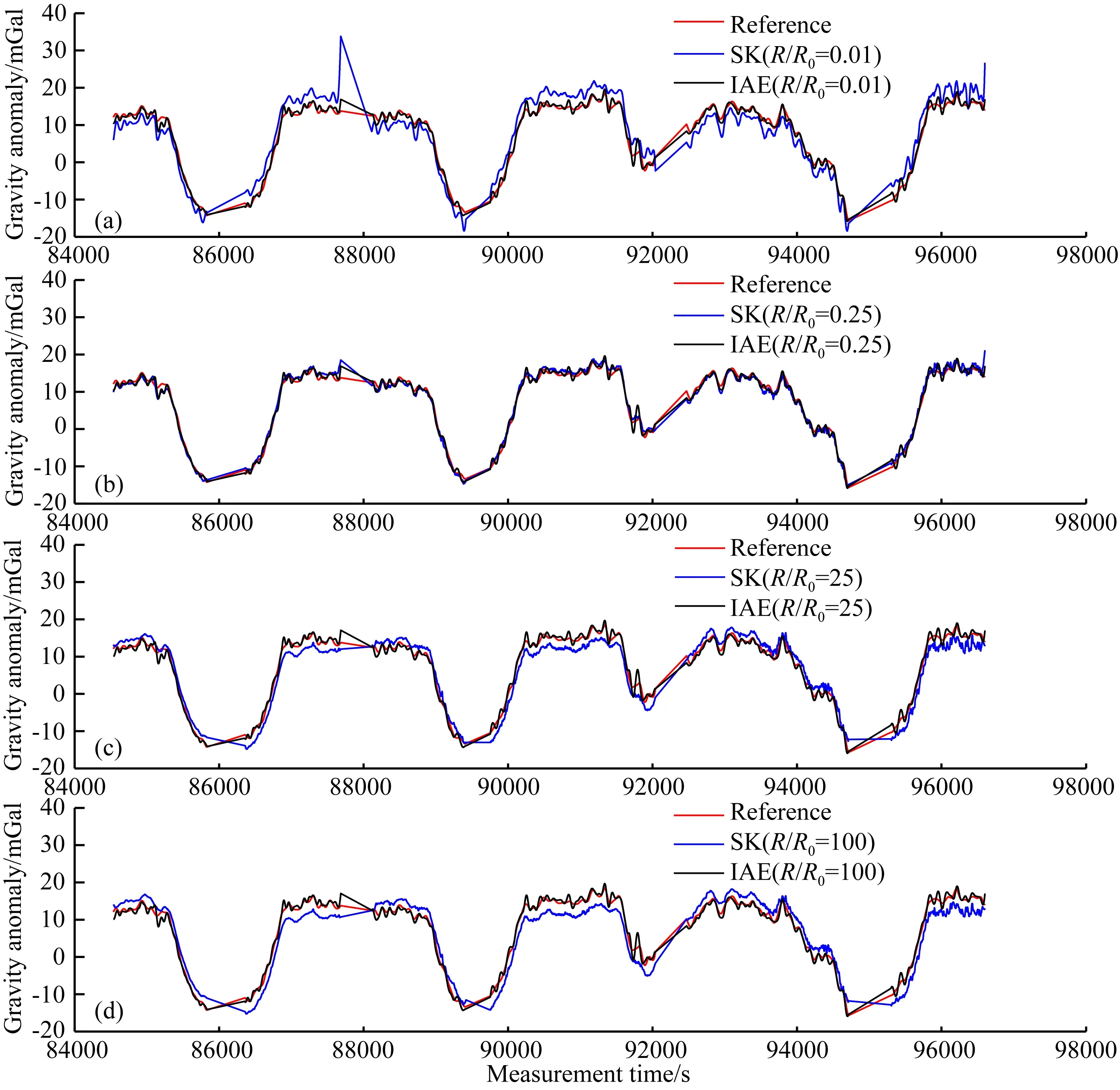
图5　SK、IAE与解算参考标准解对比图(a) R/R0=0.01； (b) R/R0=0.25； (c) R/R0=25； (d) R/R0=100.Fig.5　Airborne gravity anomaly of SK、IAE VS reference

4.3不同滑动窗口的航空重力异常解算试验

由IAE算法步骤可知，滑动采样窗口宽度N直接关系到新息协方差估计的结果，不当的滑动采样窗口也会导致IAE解算精度的下降.本部分将利用不同滑动窗口的IAE滤波器和改进IAE滤波器进行解算试验，验证改进IAE滤波器的优化效果，并讨论N对IAE解算重力异常精度的影响.试验中，IAE滤波器的滑动采样窗口取N=40、80、120、160、200分别进行解算；改进IAE滤波器的新息协方差估计器设定为5个，各新息协方差估计器的采样窗口分别为N1=40，N2=80，N3=120，N4=160，N5=200.

图6为不同滑动窗口的IAE滤波器估计的量测噪声协方差.由图可见，在测线上进行飞行测量时，飞机的运动状态平稳，此时量测噪声协方差估计曲线变化平缓；当飞机由一条测线转飞向另一条测线时(A、B、C、D、E指示的部分)，飞机的运动状态变化剧烈，量测噪声协方差估计曲线出现较大的跳动，而且曲线的跳动频率和幅度随着滑动窗口宽度的增加而减小，即滑动窗口越宽，IAE对量测噪声的估计越平稳，反之，IAE估计的量测噪声曲线跳变越剧烈.

统计不同滑动窗口的IAE与改进IAE的解算误差，如表2所示.不难看出，在N=80时，IAE的解算输出与解算参考标准的误差最小，此时的滑动采样窗口宽度兼顾了系统的运动状态变化和新息协方差估计的准确性；而在其他采样窗口宽度条件下，IAE的解算结果误差均高于N=80的情况.这也印证了前述的滑动窗口宽度选取的不宜太大也不宜太小.

注意到利用改进IAE解算的重力异常与参考标准的均方误差在1.021047 mGal，解算精度劣于N=80时IAE的解算结果，但优于其他的滑动窗口宽度的情况.因此，改进的IAE可以减小由于滑动采样窗口宽度选取不当引起的解算误差.

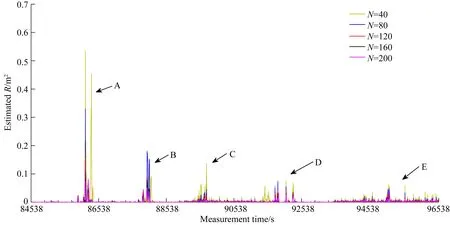
图6　IAE估计R变化曲线(N=40、80、120、160、200)Fig.6　Estimated R by IAE (N=40,80,120,160,200)

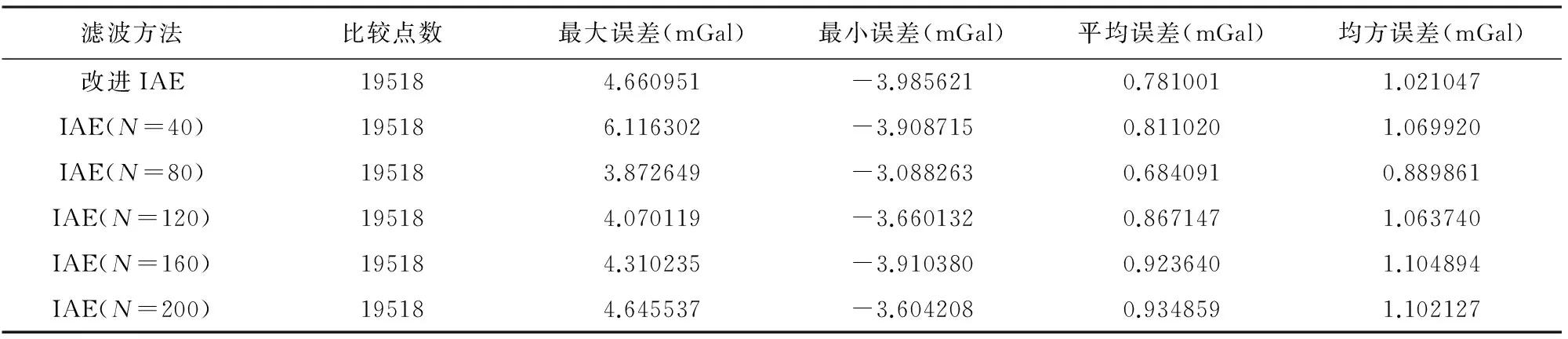
滤波方法比较点数最大误差(mGal)最小误差(mGal)平均误差(mGal)均方误差(mGal)改进IAE195184.660951-3.9856210.7810011.021047IAE(N=40)195186.116302-3.9087150.8110201.069920IAE(N=80)195183.872649-3.0882630.6840910.889861IAE(N=120)195184.070119-3.6601320.8671471.063740IAE(N=160)195184.310235-3.9103800.9236401.104894IAE(N=200)195184.645537-3.6042080.9348591.102127

5结语

本文利用新息自适应卡尔曼滤波器及改进的新息自适应卡尔曼滤波器实现航空重力异常解算，并得出如下结论：

(1) 新息自适应卡尔曼滤波器的应用，可以降低量测噪声协方差选取不准确造成的解算误差，减弱了解算精度对量测噪声先验统计信息的依赖性；

(2) 对新息自适应卡尔曼滤波器进行改进，即在新息自适应卡尔曼滤波器中设计多个不同采样窗口的新息协方差估计器，实现新息协方差估计器的滑动采样窗口优化.解算结果表明，改进的新息自适应卡尔曼滤波的应用能够减小由滑动采样窗口选取不当造成的解算误差.

为获得精度更高、更有普遍意义的航空重力异常解算方法，建议进一步加强对自适应卡尔曼滤波器设计方法的研究.同时，还应继续加强对航空重力测量系统的研究，进一步完善航空重力异常解算的卡尔曼滤波模型，提高解算精度.

致谢感谢中国国土资源航空物探遥感中心的熊盛青、周坚鑫、郭志宏和周锡华对本研究的大力支持和帮助.

References

Bian H W, Jin Z H, Wang J P, et al. 2006. The innovation-based estimation adaptive Kalman filter algorithm for INS/GPS integrated navigation system.JournalofShanghaiJiaotongUniversity(in Chinese), 40(6): 1000-1003, 1009.Bolotin Y V, Golovan A A, Parusniov N A. 2003. Mathematical models of airborne gravimetry systems with aided inertial platforms.MoscowUniversityMathematicsBulletin, 58(4):13-23.Bolotin Y V, Popelensky M Y. 2007. Accuracy analysis of airborne gravity when gravimeter parameters are identified in flight.JournalofMathematicalSciences, 146(3):5911-5519.

Bolotin Y V. 2009. Mathematics behind GTGRAV. Moscow: Moscow Lomonosov State University.

Bolotin Y V, Golovan A A. 2013. Methods of inertial gravimetry.MoscowUniversityMechanicsBulletin, 68(5): 117-125.

Cai S K, Wu M P, Zhang K D. 2010. A comparison of digital lowpass FIR-filters in airborne gravimetry.GeophysicalandGeochemicalExploration(in Chinese), 34(1):74-78.

Cai S K, Wu M P, Zhang K D, et al. 2013. The first airborne scalar gravimetry system based on SINS/DGPS in China.ScienceChinaEarthSciences, 56(12): 2198-2208.

Guo Z H, Luo F, An Z F. 2007. Experimental researches on FIR lowpass digital filters based on window functions of airborne gravity data.GeophysicalandGeochemicalExploration(in Chinese), 31(6):568-571, 576.

Guo Z H, Xiong S Q, Zhou J X, et al. 2008. The research on quality evaluation method of test repeat lines in airborne gravity survey.ChineseJournalofGeophysics(in Chinese), 51(5):1538-1543.

Guo Z H, Luo F, Wang M, et al. 2011. The design and experiment of IIR lowpass digital filters for airborne gravity data.ChineseJournalofGeophysics(in Chinese), 54(8):2148-2153.

Li R. 2014. Research of gravity anomaly solution in airborne gravimetry based on Kalman filtering [Master′s thesis] (in Chinese). Beijing: China University of Geosciences Beijing.

Luo F, Guo Z H, Luo Y, et al. 2012. Experimental researches on FIR lowpass filter based on equiripple.GeophysicalandGeochemicalExploration(in Chinese), 36(5): 856-860.

Mohamed A H. 1999. Optimizing the estimation procedure in INS/GPS integration for kinematic applications [Ph. D. thesis]. Calgary: Canada Calgary University.

Mohamed A H, Schwarz K P. 1999. Adaptive Kalman Filtering for INS/GPS.JournalofGeodesy, 73(4): 193-203.

Pan Y B. 2012. The Kalman filter method of free air anomaly solution in airborne gravimetry [Master′s thesis] (in Chinese). Beijing: China University of Geosciences Beijing.

Qin Y Y, Zhang H Y, Wang S H. 2012. Kalman Filter and Principle of Integrated Navigation 2nded (in Chinese). Xi′an: Northwestern Polytechnical University Press.Sun Z M. 2004. Theory, methods and applications of airborne gravimetry [Ph. D. thesis] (in Chinese). Zhengzhou: PLA Information Engineering University.

Tan F J, Xu J N, Li A, et al. 2009. Innovation-based adaptive Kalman filter for accelerometer signal de-noising.JournalofDataAcquisitionandProcessing(in Chinese), 24(2): 227-231.Wang J B, Xiong S Q, Zhou X H, et al. 2009. The advances in the study of the airborne gravimetry system.GeophysicalandGeochemicalExploration(in Chinese), 33(4): 368-373.

Wang J B, Xiong S Q, Guo Z H, et al. 2010. Estimation of the vertical acceleration for the airborne gravimetry using Kalman smoothing.ProgressinGeophysics(in Chinese), 25(3): 968-974, doi: 10.3969/j.issn.1004-2903.2010.03.035.

Wang J B. 2010. Methodologies and technology of data processing for airborne gravimetry [Ph. D. thesis] (in Chinese). Beijing: China University of Geosciences Beijing.

Wang J B, Xiong S Q, Guo Z H, et al. 2011. Research on methods for estimating airborne gravity anomalies.GeophysicalandGeochemicalExploration(in Chinese), 35(4): 493-498.

Xiong S Q. 2009a. The present situation and development of airborne gravity and magnetic survey techniques in China.ProgressinGeophysics(in Chinese), 24(1): 113-117.

Xiong S Q. 2009b. The strategic consideration of the development of China′s airborne geophysical technology.GeologyinChina(in Chinese), 36(6):1366-1374.

Xiong S Q, Zhou X H, Guo Z H, et al. 2010. Theory, Method and Application of Airborne Gravity Prospecting (in Chinese).Beijing: Geology Publishing.

Yue X K, Yuan J P. 2005. An adaptive Kalman filtering algorithm based on maximum-likelihood criterion.JournalofNorthwesternPolytechnicalUniversity(in Chinese), 23(4): 469-474.Zhang C D. 2005. On the subject of airborne gravimetry and airborne gravity gradiometry.ChineseJournalofEngineeringGeophysics(in Chinese), 2(4):282-291.Zheng W, Zhang G B, Li R. 2014. Application of Kalman filtering and smoothing for airborne gravimetry.AppliedMechanicsandMaterials, 548-549:1192-1195.

Zhou W, Cai T J. 2013. Study on filtering methods of airborne gravity.AppliedMechanicsandMaterials, 333-335:516-521.

附中文参考文献

卞鸿巍, 金志华, 王俊璞等. 2006. 组合导航系统新息自适应卡尔曼滤波算法. 上海交通大学学报, 40(6): 1000-1003, 1009.

蔡劭琨, 吴美平, 张开东. 2010. 航空重力测量中FIR低通滤波器的比较. 物探与化探, 34(1): 74-78.

郭志宏, 罗锋, 安战锋. 2007. 航空重力数据窗函数法FIR低通数字滤波试验. 物探与化探, 31(6): 568-571.

郭志宏, 熊盛青, 周坚鑫等. 2008. 航空重力重复线测试数据质量评价方法研究.地球物理学报, 51(5):1538-1543.

郭志宏, 罗锋, 王明等. 2011. 航空重力数据无限脉冲响应低通数字滤波器设计与试验研究. 地球物理学报, 54(8): 2148-2153.

李瑞. 2014. 基于卡尔曼滤波的航空重力异常解算的研究[硕士论文]. 北京: 中国地质大学(北京).

罗峰, 郭志宏, 骆遥等. 2012. 航空重力数据的等波纹FIR低通滤波试验. 物探与化探, 36(5): 856-860.

潘炎冰. 2012. 航重测量中解算自由空气异常的卡尔曼滤波方法[硕士论文]. 北京: 中国地质大学(北京).

覃方君, 许江宁, 李安等. 2009. 基于新息自适应卡尔曼滤波的加速度计信号降噪. 数据采集与处理, 24(2): 227-231.

秦永元, 张洪钺, 汪叔华. 2012. 卡尔曼滤波与组合导航原理(第二版). 西安: 西北工业大学出版社.

孙中苗. 2004. 航空重力测量理论、方法及应用研究[博士论文]. 郑州: 解放军信息工程大学.

王静波, 熊盛青, 周锡华等. 2009. 航空重力测量系统研究进展. 物探与化探, 33(4): 368-373.

王静波, 熊盛青, 郭志宏等. 2010. 利用Kalman平滑技术估算航空重力测量中的载体垂直加速度. 地球物理学进展, 25(3): 968-974, doi: 10.3969/j.issn.1004-2903.2010.03.035.

王静波. 2010. 航空重力测量数据处理方法技术研究[博士论文]. 北京: 中国地质大学(北京).

王静波, 熊盛青, 郭志宏等. 2011. 航空重力异常估计方法研究. 物探与化探, 35(4): 493-498.

熊盛青. 2009a. 我国航空重磁勘探技术现状与发展趋势. 地球物理学进展, 24(1): 113-117.

熊盛青. 2009b. 发展中国航空物探技术有关问题的思考. 中国地质, 36(6): 1366-1374.

熊盛青, 周锡华, 郭志宏等. 2010. 航空重力勘探理论方法及应用. 北京: 地质出版社.

岳晓奎, 袁建平. 2005. 一种基于极大似然准则的自适应卡尔曼滤波算法. 西北工业大学学报, 23(4): 469-474.

张昌达. 2005. 航空重力测量和航空重力梯度测量问题. 工程地球物理学报, 2(4): 282-291.

(本文编辑胡素芳)

Application research on adaptive Kalman filtering for airborne gravity anomaly determination

ZHENG Wei1, 2, ZHANG Gui-Bin1*

1DepartmentofGeophysicsandInformationTechnology,ChinaUniversityofGeosciences,Beijing100083,China2DepartmentofInformationEngineering,HenanInstituteofScienceandTechnology,XinxiangHenan453003,China

AbstractBased on the basic principle of airborne gravimetry, Kalman filtering model for airborne gravity anomaly determination is established and innovation-based adaptive estimation Kalman filter (IAE) is applied to estimate the airborne gravity anomaly when measurement covariance is unknown. At the same time, improved IAE filter installing several innovation covariance estimators is designed to reduce the difficulty of sampling window width selection. It is can be seen from the experimental result that IAE is able to reduce gravity anomaly determination errors caused by lack of statistical information of measurement noise. Moreover, the improved IAE filter can decrease the rate of determination errors introduced by the improper selection of sampling window width, and the error of gravity anomaly determined by improved IAE is nearly 1 mGal.

KeywordsAirborne gravity anomaly determination； Adaptive Kalman filtering； Innovation； Covariance of measurement noise

基金项目国家高技术研究发展计划(863计划)(2011AA060501)资助.

作者简介郑崴，男，1984年生，博士，主要从事航空重力测量技术的研究. E-mail:13667060@qq.com *通讯作者张贵宾，男，1958年生，教授. 主要从事地球物理反演、重磁电勘探等研究. E-mail:gbzhang@cugb.edu.cn

doi:10.6038/cjg20160410 中图分类号P223,P631

收稿日期2015-09-14，2015-12-24收修定稿

郑崴， 张贵宾. 2016. 自适应卡尔曼滤波在航空重力异常解算的应用研究. 地球物理学报，59(4):1275-1283,doi:10.6038/cjg20160410.

Zheng W, Zhang G B. 2016. Application research on adaptive Kalman filtering for airborne gravity anomaly determination.ChineseJ.Geophys. (in Chinese),59(4):1275-1283,doi:10.6038/cjg20160410.