基于正弦函数处理新息的船舶模型参数辨识新算法
张显库,祝慧颖
大连海事大学 航海学院,辽宁 大连 116026
0 引 言
船舶的运动数学模型是船舶操纵性能预测、航海仿真和船舶运动控制器设计的基础,具有10 个参数以上的Norrbin 或MMG 非线性数学模型的精度较高,但比较复杂;简单的线性Nomoto 模型只有2 个参数,但精度稍低;具有4 个参数的非线性Nomoto 模型介于上述两类模型之间,精度较高且不复杂,被船舶运动控制学者广泛关注。非线性Nomoto 模型中的2 个非线性参数一般通过系统辨识获得。新船在出厂后,通常只按国际标准要求做了满舵回转实验和部分Z 形操纵实验,如果采用此少量的船舶试验数据进行系统辨识研究,给出船舶模型参数,其精度与用经验公式估算的结果相近,不适用于模型精度要求较高的系统仿真或控制器设计。
目前,常用的系统辨识算法主要有最小二乘法、梯度辨识法、辅助模型辨识法等,这些算法都是利用典型的辨识数据进行系统的参数辨识。丁锋[1]提出的系统辨识新论,将标量的误差信息(也可称为新息)变成了误差信息向量,称为多新息辨识算法,取得了较好的理论与应用成果;徐玲[2]利用动态窗数据将随机梯度参数辨识方法中的标量新息扩展为新息向量,提出传递函数多新息随机梯度参数估计方法,进一步提高了辨识精度;谢朔等[3]提出的一种改进的多新息扩展卡尔曼滤波参数辨识方法,通过引入遗忘因子以降低历史干扰数据的累积影响,经此改进算法辨识的船舶响应模型参数更加精确;时振伟等[4]针对多元线性或非线性回归系统,将耦合辨识思想与带遗忘因子的有限数据窗辨识理论相结合,提出一种耦合带遗忘因子有限数据窗递推最小二乘辨识算法,该算法计算效率高,能够快速跟踪时变参数,获得精确的参数估计;孙功武等[5]提出了一种基于模糊控制的动态遗忘因子递推最小二乘算法,该算法中的遗忘因子能够根据参数辨识误差进行实时修正, 但仅对单输入输出系统模型参数进行了辨识研究;刘艳君等[6]针对含有未知时滞的多输入输出误差系统,结合正交匹配追踪算法和辅助模型思想对最小二乘迭代算法进行改进,提出了一种辅助模型正交匹配追踪迭代算法,该算法对采样数据的需求量不大,且在噪声水平不高的情况下可以获得精度较高的时滞估计与参数估计;焦慧方等[7]针对多变量耦合系统参数辨识,在传统最小二乘法基础上,提出了一种带遗忘因子交替广义最小二乘法,实现了无偏估计,并且简化了计算;黄旭等[8]基于多新息辨识理论与随机梯度辨识算法理论,结合变遗忘因子,提出了基于变遗忘因子多新息随机梯度算法的双馈电机参数辨识方法,相比最小二乘辨识方法减少了计算工作量,相对于随机梯度辨识方法提高了辨识速度;郑涵等[9]针对传统扩展卡尔曼滤波方法的不足, 提出了一种新型的反馈粒子滤波算法,其收敛速度更快,稳定性更好,并应用到船舶运动数学模型的参数辨识中。以上文献的研究重点集中在提高收敛速度、辨识效率和辨识精度方面,取得了一定的研究成果,但是在样本数据较少的情况下,辨识效果并不理想。Zhang 等[10-11]提出了非线性反馈控制的思想,用非线性函数处理误差并用于船舶运动控制,取得了良好的控制及节能效果。
本文将结合新息辨识算法[1]和非线性反馈控制[10-11]2 种创新思想,在最小二乘算法的基础上,采用非线性正弦函数对新息进行处理后再进行参数辨识,通过仿真试验验证该算法在数据样本少的情况下的计算速度及辨识精度,以期改善最小二乘辨识算法在数据样本少时的辨识精度。
1 问题分析
图1 给出了非线性新息辨识算法计算过程示意图。其主要原理为对最小二乘等传统辨识算法进行改进,将其误差信息(新息)用正弦函数进行非线性处理,其他辨识过程保持不变,使用小样本数据即可辨识出较为准确的结果。

图1 非线性新息辨识算法计算过程示意图Fig. 1 Schematic diagram of calculation process of nonlinear innovation identification algorithm
2 船舶数学模型的建立


图2 非线性的船舶运动数学模型Fig. 2 Nonlinear mathematical model of ship motion

3 非线性新息改进的最小二乘算法
常规的最小二乘法 (least square,LS) ,如式(3)所示:

多新息最小二乘法(muli-innovation least square,MILS)[1],将最小二乘递推算法中每次递推使用的单新息标量扩展为一定长度的多新息向量,从而在保证辨识精度的前提下提高参数在线辨识的收敛速度。本研究受其思想启发将新息进行非线性处理。
式(5)中,Ud未经任何处理,直接参与系统辨识。受到非线性反馈方法的启发,将新息经正弦函数的非线性处理后再参与模型参数辨识,非线性辨识参数的算法调整为式(6):

4 仿真验证与结果分析
4.1 “育鲲”船
本文以大连海事大学教学实习船“育鲲”船为对象建立船舶数学模型,数学模型采用式(1)的非线性Nomoto 模型,船舶参数如表1 所示。

表1 “育鲲”船船舶参数Table 1 Yukun ship particulars
“育鲲”船的非线性Nomoto 模型参数(K,T,α, β)的真值可根据表1 给出的船舶参数通过理论计算得出[13-14],结果如表2 所示。

表2 “育鲲”船模型参数真值Table 2 True value of Yukun ship model parameters


利用获得的26 组仿真数据进行 α,β的非线性参数辨识,用于验证辨识算法精度是否满足要求。对于α 的辨识A=1,ω=0.87;对于β的辨识A=1.45,ω=1.14。比较最小二乘法和非线性新息改进的最小二乘法对非线性参数 α、β 的辨识效果,结果如图3 所示。由图3 可见,最小二乘法的辨识结果中α=15.94,β=17 220.81,α 和β 的误差分别为12.1% 和23.3%,平均误差17.7%;非线性函数改进的最小二乘法的辨识结果中α=14.11,β=21 729.58,α 和β 的误差分别为0.8% 和3.2%,平均误差只有2.0%,模型辨识精度可达98.0%。
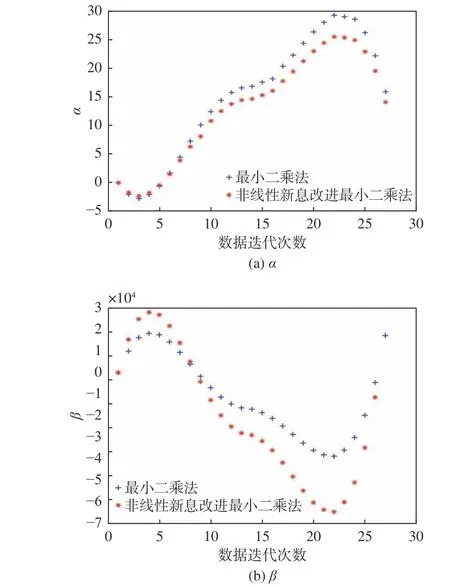
图3 最小二乘法和非线性新息改进最小二乘法对“育鲲”船的辨识效果Fig. 3 Identification effect of LS method and nonlinear innovation improved LS method on Yukun ship
由此可见,在只有26 组仿真数据的前提下,非线性新息改进的最小二乘法具有较高的辨识精度,相对于最小二乘法的辨识精度提高了15.7%。
4.2 “育鹏”船
为了进一步检验非线性新息改进最小二乘法的辨识效果,采用大连海事大学另一艘教学实习船“育鹏”船进行验证,A,ω 保持不变。“育鹏”船的船舶参数和模型参数真值如表3 和表4 所示。

表3 “育鹏”船船舶参数Table 3 Yupeng ship particulars

表4 “育鹏”船模型参数真值Table 4 True value of Yupeng ship model parameters
同理,用最小二乘法和非线性新息改进最小二乘算法对“育鹏”船的非线性参数 α,β进行辨识,结果如图4 所示。

图4 最小二乘法和非线性新息改进最小二乘法对“育鹏”船的辨识效果Fig. 4 Identification effect of LS method and nonlinear innovation improved LS method on Yupeng ship
由图4 可见,最小二乘法的辨识结果中α=13.59,β=19 270.41,α 的误差为13.7%,β 的误差为19.5%,平均误差16.6%;非线性新息改进最小二乘法辨识结果中α=12.12,β=25 342.29,α 的误差为1.4%,β 的误差为5.9%,平均误差3.7%,即模型辨识精度可达96.3%。
因此,在样本数据较少的情况下,以“育鹏”船为对象进行仿真验证,非线性新息改进最小二乘算法的辨识精度仍然比最小二乘法的提高了12.9%,进一步证明了该算法的有效性和普适性。此外,本算法因只需要少量的数据样本,计算量减少,故客观上提升了辨识速度。
5 结 论
本文将多新息系统辨识和非线性反馈控制思想相结合,提出了一种基于非线性新息的船舶模型参数辨识算法。通过对比和辨识仿真验证,得出了以下结论:
1) 该算法辨识所需样本数据较少。在仿真验证过程中只采用了26 组仿真数据,辨识准确度可达到96%以上,为小样本数据情况下的参数辨识提供了参考。
2) 通过2 艘船的辨识验证,该算法比最小二乘法的辨识精度提高了12% 以上,拓展了最小二乘法的应用范围。
3) 该算法的辨识速度较快。
本研究给定模型参数,是为了验证辨识算法的有效性和准确性,下一步可实际采集少量实船试验数据样本,用本研究结果直接辨识船舶模型,以克服理论计算模型计算复杂且精度不高的缺点。此外,还可将多新息和非线性新息相结合,进行多模型、多参数的船舶模型辨识研究。

