基于格子Boltzmann 方法的液润表面减阻规律

秦声雷，侯国祥，郭文强，周斌斌，姜思远

华中科技大学 船舶与海洋工程学院，湖北 武汉 430074

0 引 言

经典的流体力学假设固液边界为无滑移边界条件，即壁面的切向速度恒为零，固液界面不发生滑移。这种假设在宏观上得到验证，并被广泛应用于科学分析和工程应用中。但是有研究表明[1-3]在微尺度流动中，界面上存在滑移现象。吴承伟等[4]对流动边界滑移问题进行了综述，边界滑移现象受诸多因素影响，如表面粗糙度、液体粘性、接触角、速度梯度和温度等[5-8]。格子Boltzmann方法（LBM）基于分子动理学，作为一种介观方法，适用于对微尺度流动的模拟。近年来，黄桥高等[9]应用LBM 的伪势模型[10-11]对超疏水表面减阻特性进行研究，得出表观滑移发生在近壁区低密度层上的结论。王凯等[12]应用LBM，对固液界面滑移现象的影响因素进行了研究，表明滑移长度不显著依赖于剪切率。

传统的减阻理论认为，超疏水表面在水下可以形成气膜层而不与外层液体直接接触，原来的固液接触面变为气液接触面，使得表面承受的剪切应力大大减小，并在气液界面产生滑移速度。任刘珍等[13]综述并总结了超疏水表面减阻所面临的问题——在高剪切速率和高压作用下气液界面会发生失稳，从而导致减阻效果不佳。吕鹏宇等[14]对气液界面的稳定性和演化规律进行了总结。事实上，将微结构中的气体替换为润滑油，可以在保持良好减阻特性的同时，还较大地保证滑移界面的稳定性。Wong 等[15]合成了一种液润多孔表面（SLIPS），发现这种表面能使液滴具有极小的滚动角、可以承受高压和冲击（氮气环境中达到676 atm）、具有良好的自我修复性和光学透明性。这种新型表面被称为液润表面（liquidinfused surface，LIS），在抗冰、防污、减阻等研究领域引起了广泛的关注。在减阻方面，Solomon等[16]通过改变油液粘性比，在动力粘性比为260 时，得到了18 µm 的滑移长度，减阻效率为16%。Rosenberg 等[17]设计了一组粘性比为0.3～1.4，沟槽尺度为100～800 µm 的液润表面，发现当粘性比越大、沟槽宽度越宽、雷诺数越大时，减阻效果越好，但在个别极端的情况下会出现反常。Chang等[18]的研究也表明减阻效果会随沟槽宽度的增加而增加，但受沟槽深度的影响较小。

现有的研究主要是针对液润表面的沟槽形式、尺寸、油液粘性比等对减阻效果的影响，研究的假设也都是油液绝对不溶。事实上，不存在绝对不溶的物质，难溶具有相对性。本文基于LBM，主要从润滑油难溶性方面，对润滑油的减阻规律进行探究，为设计适当的微表面结构提供参考意见。

1 数值方法

1.1 格子Boltzmann 方法

采用单松弛的格子Boltzmann 方法（LBGK）[19]，其不含源项演化方程为

1.2 Shan-Chen 多组分模型

1.3 模型有效性验证

组分间分子作用力的引入引起了动量的变化，上式添加力项有

设置150 ×150 的计算域，中心处设置半径不等的圆域（图1）。圆域内设置组分1 密度为1.0、组分2 密度为0，圆域外设置组分2 密度为1.0、组分1 密度为0，组分间作用强度Gc设置为1.85。左右为周期边界，上下为非平衡态反弹格式[21]。最终得到内外压强差dp和半径倒数1/r的关系，如图2 所示（本文数值模拟中变量单位均为格子单位，直线为辅助视图）。图2 中dp和1/r之间为线性关系，且连线经过原点，这表明数值模拟结果与式（26）一致。据此，可以计算出此时的表面张力为0.085。由理论分析和数值模拟结果可知，此多组分模型能够有效反映不同组分间的作用力，可以用来模拟油液分界面上产生的疏水减阻现象。

图1 计算模型示意图Fig. 1 Sketch of computational model

图2 G c=1.85时液滴dp 和1/r 的关系Fig. 2 The relationship between pressure difference dp and reciprocal radius 1/r with parameter Gc=1.85

2 数值模拟

2.1 壁面润湿性数值模拟

壁面的润湿性可由接触角GA来描述，当GA大于90°时表现为疏水，小于90°时表现为亲水。其疏水特性可以通过调整壁面作用强度Gads,σ实现模拟。采用200×100 的计算区域，左右采取周期边界，上下采取非平衡态反弹格式（图3）。初始化时，在距壁面0.85R处放置一个半径R=40的圆域。在圆内设置组分1 的密度为1.0，组分2的密度为0。在圆外设置组分1 密度为0，组分2的密度为1.0。组分分子间作用强度Gc取1.85，弛豫时间均取1.0。得到结果如图4 和图5 所示。

图3 计算模型示意图Fig. 3 Sketch of computational model

图4 不同壁面参数G ads,σ时的接触角Fig. 4 Contact angle with different wall parameters Gads,σ

图5 不同壁面参数G ads,1时的接触角Fig. 5 Contact angle with different wall parameters Gads,1

从图5 可以观察到，随着壁面参数Gads,1的不断变大，其对应的接触角也不同程度地增大。结果表明接触角的大小与壁面参数Gads,1有正相关关系。从物理层面上来说，壁面参数Gads,1反映固液界面排斥力的大小，Gads,1越大，排斥力越大，壁面疏水性自然也越强。因此接触角与Gads,1具有正相关关系。

2.2 润滑油溶解变化数值模拟

在Shan-Chen 模型[20]中Gc存在一个临界值Gc,crit=1/(ρ1+ρ2)， 当Gc小 于Gc,crit时，两组分会发生混溶，并产生稳定的溶解密度解。当Gc大于Gc,crit时，组分之间会发生分离并形成稳定界面。由于计算模型并不复杂，且横向采用周期边界条件，为节省计算资源，采用较小的30×100 的计算域，上下采用非平衡态反弹格式，Gads,σ取为0。初始设置为上半平面只有组分1，下半平面只有组分2（润滑油），密度皆为1.0（图6）。得到结果如图7 和图8（a）所示。

图6 计算模型示意图Fig. 6 Sketch of computational model

图7 润滑油密度分布图Fig. 7 The distribution of lubricant

图8 润滑油在上半平面的溶解密度 ρ2和 组分间作用强度 Gc 的关系图（虚线为辅助视图）Fig. 8 The relationship between parameter G c and lubricant's dissolved density in half upper space (the dotted line is for auxiliary view)

从图7(a)中可以看出，当Gc=1.0，润滑油完全溶于组分1 中，两组分之间不能形成稳定界面。当Gc>1.0，组分之间可以形成稳定界面，且润滑油在上半平面的溶解密度随着Gc的增加迅速下降，并在Gc=1.8 附近逐渐趋于零。图8（b）重画了文献[22] 中 ρtotal=2的 部 分 图 像（原 文 ρtotal用 ρi表 示，本文 ρtotal=1），对比结果，本文与文献[22]一致。

2.3 微结构液润表面滑移流动数值模拟

为了验证液润表面确实具有减阻效果，我们设置了计算域为330×250，沟槽深度为20，宽度为30，沟槽内设置组分2 为润滑油，外部流场设置为组分1。为简便起见，各组分密度均设置为1.0，初始溶解密度均为0.02。左右为周期边界，壁面采用标准反弹格式。为了满足LBGK 的低马赫数条件，顶部（Y=250）水平速度设置为0.01（图9），并采用非平衡态外推格式[23]。取Gc= 1.8，Gads,1=0.2，Gads,2=−0.2。

图9 计算模型示意图Fig. 9 Sketch of computing model

达到平衡状态时，外部流动区域组分1 密度为0.991，组分2 溶解密度为0.031。沟槽内组分2密度为0.98，组分1 溶解密度约为0.032 7。将收敛后计算域中所有组分2 密度求和约为5 586.44，与初始设置的组分2 总质量29×20×7+0.02×230×331=5 582.6 对比，相对误差为 6.87×10−4，仍然满足质量守恒。模拟结果如图10 所示，图中微沟槽用黑色标记。

图10 微结构密度分布图Fig. 10 The density distribution of the microstructure with microflow

从图10（c）可以看到，在微结构及润滑油的表面上明显存在一层低密度层，而表观滑移则是发生在低密度层之上[9]。对低密度层外的速度进行线性拟合并向实际流场区域外扩展，速度等于0 的位置与壁面的距离即为滑移长度。最终得到中段处滑移长度为1.06。数值模拟结果表明液润表面确实可以产生滑移现象，具有减阻的作用。为了进一步探讨润滑油溶解性质对滑移长度的影响，我们简化了模型——Couette 流，将在后文介绍。

2.4 溶解密度对滑移长度的影响

在Shan-Chen 模型中，溶解密度和组分分子间作用强度Gc有 关，Gc越大组分分子间作用强度越强，溶解密度越小。因此可以用Gc来表征组分的溶解性质。溶解密度和Gc的关系可以由图8（a）得到。为了减小壁面影响，仅考虑润滑油溶解密度对滑移长度的影响，设置壁面参数Gads,1和Gads,2为0。此时壁面表现为既不亲水也不疏水。算例为30×100 的Couette 流，顶部剪切速度恒为0.01，上半平面只有组分1，下半平面只有组分2（润滑油），密度皆为1.0，左右为周期边界，上下为非平衡态反弹边界（图11）。通过改变组分间作用强度Gc的大小，可得图12 所示的关系。值得注意的是，曲线在Gc=1.0时出现了斜率不连续点，这是因为两种液体完全混溶，分界面突然消失（图7（a））。

图11 计算模型示意图Fig. 11 Sketch of computational model

图12 中曲线第1 段具有较好的线性规律，此时2 种液体完全混溶，不存在分界面。当Gc=0时，算例等效于单组分的Couette 流，滑移长度b为0。当Gc≠0时，由于壁面附近粒子受上方其他组分粒子的排斥力，组分1 和2 的粒子会聚集在壁面，造成壁面总密度较大（图13（a）～图13（c）和图14），形成一层高密度区，表现为增阻。组分间作用强度越大，壁面总密度越高（图13（a）～图13（c）），滑移长度越小。

图12 G ads,1=−Gads,2=0 时滑移长度b 和组分间作用强度G c 的关系（直线为辅助视图）Fig. 12 The relationship between slip length b and cohesion force strength Gc with wall parameter Gads,1=−Gads,2=0 (the straight line is for auxiliary view)

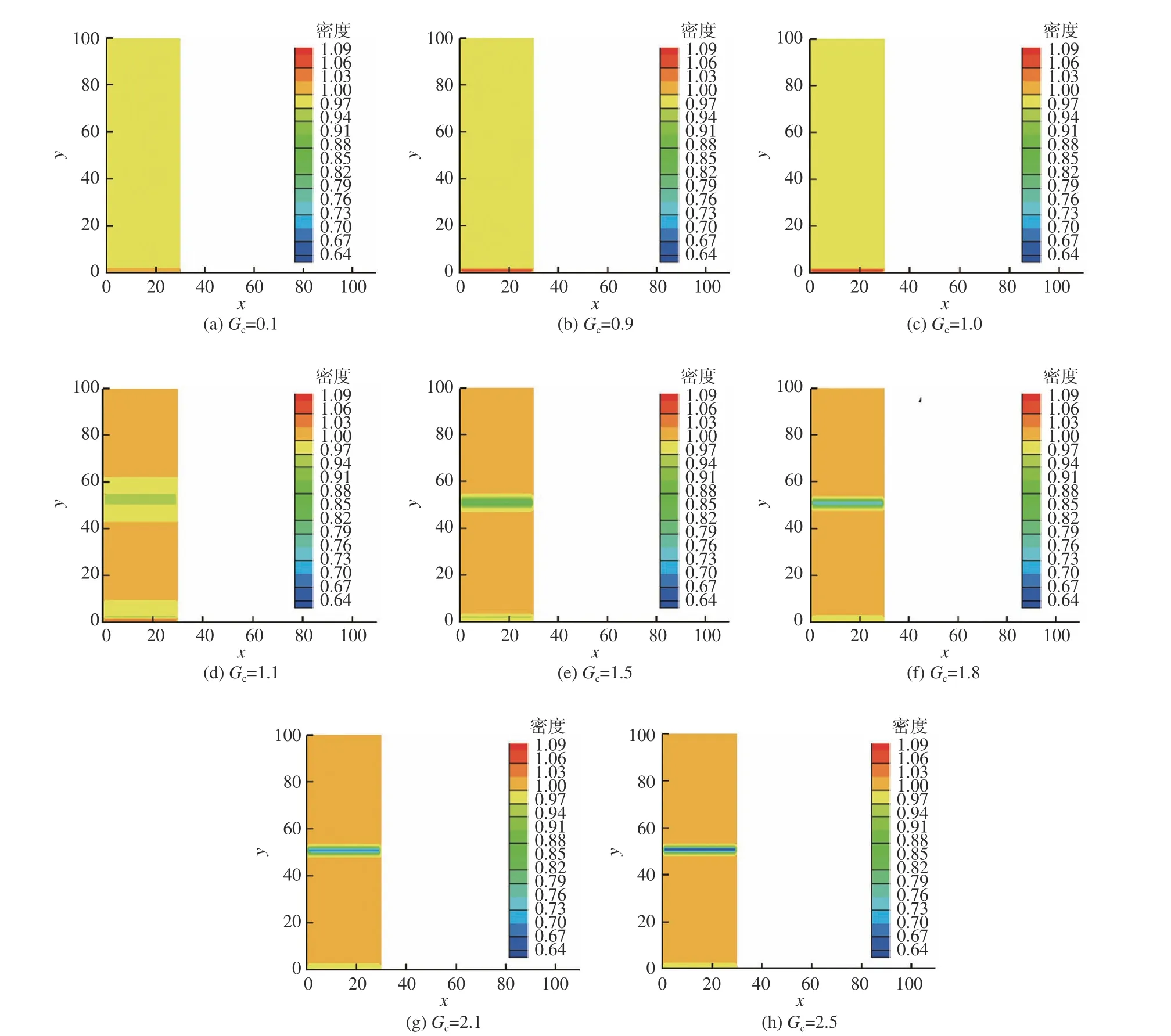
图13 不同组分间作用强度G c时的总密度分布图Fig. 13 Total density distribution with different cohesive force strength Gc

图14 G c=0.1， Gads,1=−Gads,2=0时 密 度 沿y 方 向 分 布 图（ ρ1和 ρ2分别代表组分1、组分2 密度）Fig. 14 Density value along y axis with parameters Gc=0，Gads,1=−Gads,2=0

曲线的第2 段约从Gc=1.0 到Gc=1.8，为非线性。导致非线性的原因主要是2 个方面。一方面是因为此阶段溶解密度的下降表现为非线性（图8），另一方面壁面附近的密度层逐渐从高密度层转为低密度层（后文将说明）。此阶段组分在彼此之间的溶解密度迅速下降（图8），分界面上的排斥力快速增长，导致中央区域总密度降低（图13（d）～图13（f）），表现为滑移长度的增加。

曲线的第3 段具有较好的线性规律，此时组分间的溶解密度达到极小，且趋于0，溶解密度不再随Gc发生显著变化（图8），界面上的排斥力主要由Gc决 定。显然排斥力和Gc为 线性关系，Gc越大，排斥力越大，中心区域界面上的总密度则越小（图13（f）～图13（h）），滑移长度越大。同时值得注意的是，壁面附近原来的高密度层已经转变为低密度层。主要原因是壁面附近组分1 和2 密度分布不均匀。当Gc较大时，在壁面附近组分2的粒子数量远远少于组分1。微量的粒子在排斥力作用下更容易聚集在壁面，而聚集在壁面的粒子又会反过来排斥组分2 的粒子，使得壁面附近组分2 密度下降。由于壁面组分2 的密度高于组分1，所以组分2 密度变化影响高于组分1，因此，总密度在壁面附近表现为低密度层（图15）。

图15 G c=1.8 ， G ads,1=−Gads,2=0时密度沿y 方向分布图Fig. 15 Density value along y axis with parameters Gc=1.8，Gads,1=−Gads,2=0

2.5 剪切率对滑移长度的影响

沿用2.4 节中的计算模型，固定Gc=1.8，并改变模型顶部的水平速度，结果如图16 所示。对于润滑油的减阻特性来说，其产生的滑移长度并不显著依赖于剪切率，这一点与传统疏水壁面减阻特性[12]相似。这一相似性，主要是因为当润滑油难溶时，油液界面可以产生较稳定的排斥力，而这与疏水壁面产生的排斥力是相似的。在稳定的排斥力作用下，滑移长度不显著依赖于剪切率。值得注意的是在文献[12] 中，水平速度保持不变，但改变竖向距离。与本文相比，虽然方式略有不同，但实质上变化的都是剪切率∂u/∂y。

图16 剪切率对滑移长度的影响Fig. 16 Influence of shearing rate on slip length

3 结 论

本文利用格子Boltzmann 方法对液润表面的滑移现象进行了数值模拟，并研究了润滑油溶解密度、剪切率对滑移长度的影响，得到如下结论：

1） 通过理论分析Shan-Chen 多组分模型压力项的表达式，以及对拉普拉斯定律的数值验证，表明Shan-Chen 多组分模型可以有效地反映不同组分间分子作用力，进而可以用来模拟油液分界面上产生的疏水减阻现象。

2） 在其他物理性质相似的情况下，润滑油难溶程度越高，油液界面上排斥力越大，诱导的低密度区密度越低，产生的滑移长度越大。

3） 在不考虑润滑油流出的情况下，液润表面产生的滑移长度不显著依赖于剪切率。