考虑腐蚀作用下的铝合金三体船疲劳强度直接计算分析

周陈炎，张佳宁，陈玲，孟巧

1 南通理工学院 电气与能源工程学院，江苏 南通 226002

2 大连海事大学 船舶与海洋工程学院，辽宁 大连 116026

0 引 言

三体船船型作为近年来研究关注的热点，具有横稳性及耐波性优良等一系列优点，在军、民用领域有着良好的应用前景。同时，为满足三体船轻量化和高性能的要求，船体材料可采用铝合金材质。针对三体船疲劳强度评估，劳氏船级社（LR）有相应的简化算法，但此规范仅针对钢制船舶而言，并不适用于铝合金三体船。随着对三体船研究的深入，国内外学者针对三体船整船疲劳强度计算的分析越来越多。李哲等[1]基于谱分析法与LR 规范法，对三体船疲劳强度进行了评估，结果显示LR 规范法的结果偏于保守。Wang[2]采用直接计算法预报了三体船典型节点的疲劳寿命，并考虑疲劳载荷的不确定性对疲劳可靠性进行了分析。甄春博等[3]基于谱分析法对三体船进行整船疲劳强度计算，分析了不同因素对疲劳损伤的影响。上述研究成果表明，谱分析法可以考虑不同航速、海况、航向等因素对三体船疲劳寿命的影响。

船舶因长期在恶劣的海况下航行，腐蚀比较严重，而腐蚀会对结构的疲劳寿命产生影响。目前，国内有关铝合金三体船在腐蚀环境下的疲劳强度评估工作开展较少，本文将以某120 m 铝合金三体船为例，利用谱分析法对铝合金三体船进行疲劳强度的直接计算，并基于不同的腐蚀模型分析腐蚀对三体船热点部位疲劳寿命的影响。

1 谱分析法基本原理

基于谱分析法的疲劳强度直接计算的基本原理是：依据某一海况分布，首先进行波浪载荷加载以及船体结构应力响应计算，得到热点应力传递函数，然后，利用传递函数结合波浪功率谱得到船体结构应力的响应谱。各短期海况应力交变过程的峰值将服从Rayleigh 分布。基于此，计算各短期范围的损伤，并加权得到总损伤。

2 计算模型及热点部位选取

2.1 计算模型

铝合金三体船计算模型分水动力模型和结构有限元模型2 种，前者为三体船湿表面模型，后为整船有限元模型。水动力模型是根据船体外表面划分而成的湿表面模型，其依据湿表面模型生成自由面网格，图1 所示为某120 m 铝合金三体船的水动力模型。三体船有限元模型能够精确模拟船舶的承载模式和变形特点，使其能够通过有限元计算来获取船舶结构响应。

2.2 热点部位选取

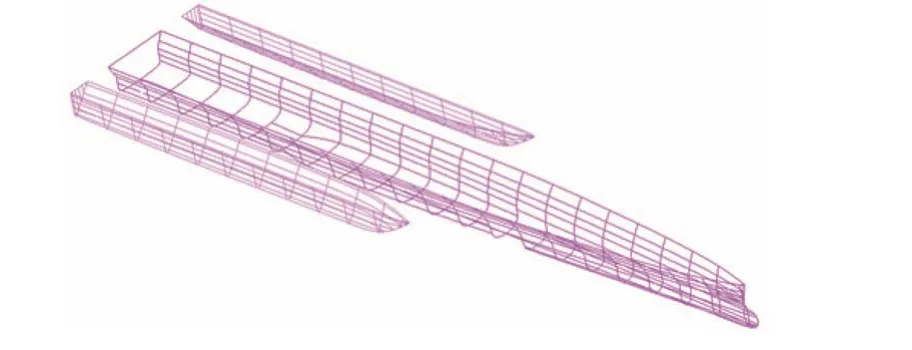
图 1 三体船水动力模型Fig. 1 Hydrodynamic model of the aluminum alloy trimaran

研究及实践结果表明[4]，三体船结构在主船体、片体、船艏、舱口位置及连接桥部位均可能存在疲劳热点。本文120 m 铝合金三体船根据三体船有限元应力计算结果，在船艉、连接桥及船身处选取了6 个疲劳热点部位（云图中应力最大点），如表1 所示。由于三体船船体外形及结构复杂，疲劳热点应力计算采用直接计算法，并将局部网格细化嵌入全船有限元模型中。限于篇幅，本文仅给出了纵骨穿越强框架处（S3）、连接桥与横舱壁相交处(S6) 的热点部位示意图，如图2所示。

表1 铝合金三体船疲劳评估热点部位Table 1 Hot spot for fatigue assessment of the aluminum alloy trimaran

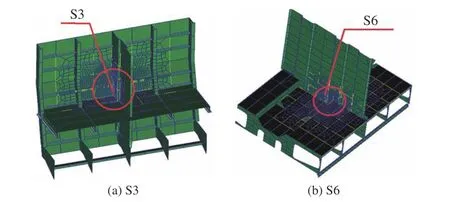
图 2 三体船热点有限元模型Fig. 2 Finite element model of the aluminum-alloy trimaran's hot spot

3 波浪载荷及应力响应计算

3.1 波浪载荷及计算工况

波浪载荷分析主要采用三维水动力分析方法。运动响应和水动压力利用软件Hydrostar 进行计算，计算航速为20 kn；考虑波浪方向，取航向角θ=0°～330°，间隔取为30°；计算波浪圆频率取ω=0.1 ～2.0 rad/s，步长0.1，共20 个计算频率。具体工况及参数如表2 所示。

表2 波浪载荷响应计算工况和参数Table 2 Calculation conditions and parameters of wave load response

3.2 应力响应传递函数

采用谱分析法计算时，计算工况较多，应力值若采用手动提取，耗时长且易出错，本文采用Patran软件自带的程序编写语言PCL 进行应力的自动提取。计算的热点部位如表1 所示。受篇幅所限，只给出了湿甲板与片体相交处(S2)、连接桥与三体船主船体相交处(S4) 的应力响应传递函数，分别如图3 和图4 所示。图中，S为疲劳热点应力。

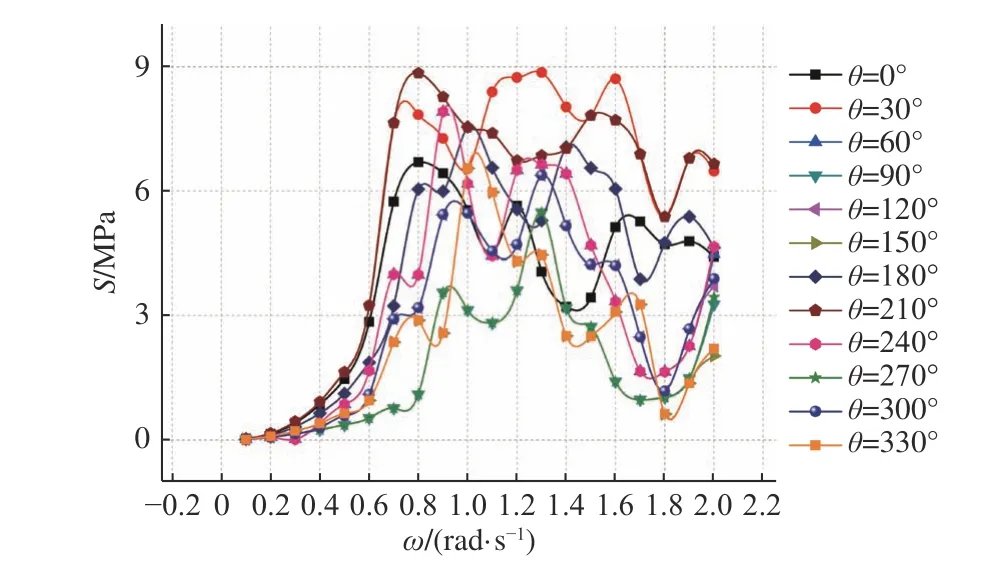
图 3 热点S2 处的应力响应传递函数Fig. 3 The stress response transfer function of S2

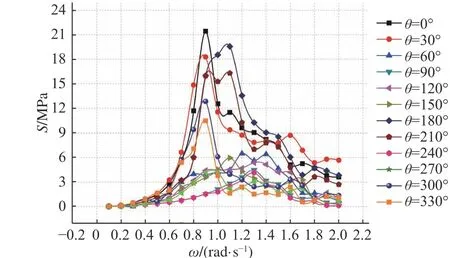
图 4 热点S4 处的应力响应传递函数Fig. 4 The stress response transfer function of S4

4 疲劳损伤及寿命计算

4.1 S-N 曲线选取

选取的S-N曲线是基于文献[5]中所述含B，C，D 的3 条S-N曲线，因本文选取的热点类型均为weld joint，故采用D 曲线。

4.2 疲劳损伤度及寿命计算

式中，m0为应力响应谱GXX(ωe)的零次距。

考虑船舶所处海况及其航向，由式（3）计算船舶疲劳损伤度Dij。

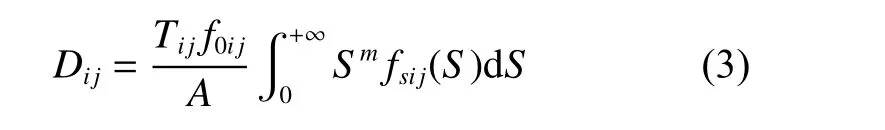
式中：m，A为S-N曲线参数；Tij为船舶i海况、j航向下的航行时间；f0ij为零穿越期望值；fsij(S)为i海况、j航向时的应力范围概率密度函数。

将式(2)代入式(3)，i海况、j航向下的疲劳损伤度Dij表达式可变为

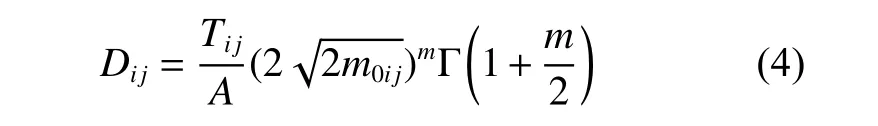
式中：m0ij为i海况、j航向下船舶应力响应谱GXX(ωe)的零次距；Γ()为伽玛函数。

根据Miner 线性累计损伤准则，船舶在设计寿命TD期间总的疲劳损伤度D为

各航向角下三体船热点部位的疲劳损伤度计算结果如图5 所示。将各航向角的疲劳损伤度线性叠加，得到如表3所示各热点的疲劳损伤度及寿命数据。

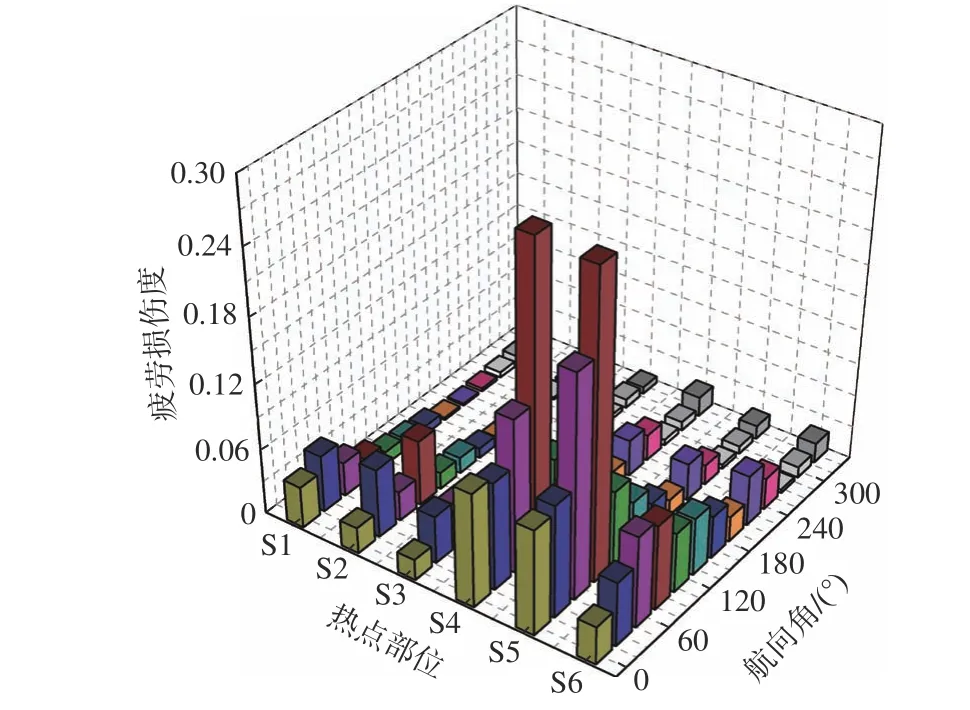
图 5 各航向角下热点部位的疲劳损伤度Fig. 5 Fatigue damage of hot spots in different heading angle

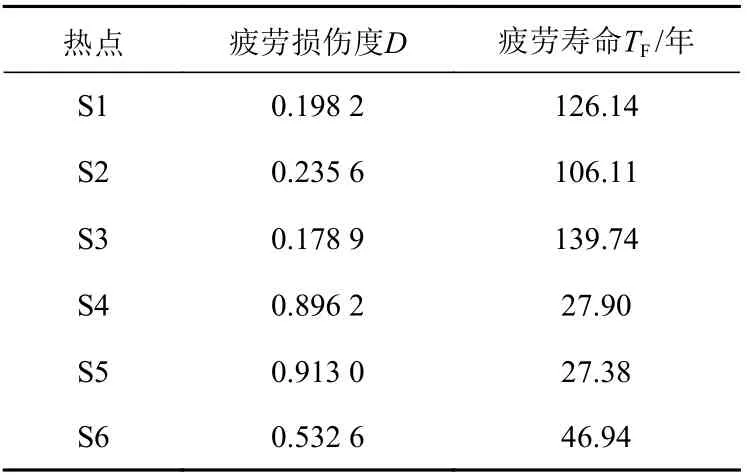
表3 基于直接计算法的铝合金三体船疲劳损伤及寿命计算Table 3 Calculation of fatigue damage and life of aluminumalloy trimaran based on direct calculation method

由表3 的计算结果可知，120 m 铝合金三体船各热点部位的疲劳寿命均超过25 年，满足规范要求。热点S1，S2，S3 处的疲劳寿命偏于安全，考虑到热点的选取全部是按照应力云图中最大应力点选取，排除了热点选择不准确的情况。由此可以得出结论，三体船连接桥部位（热点S4，S5，S6均在连接桥部位）应为疲劳评估的重点对象。

5 腐蚀对热点疲劳特性的影响

目前，有关船舶腐蚀的处理方法依旧是基于均匀腐蚀的假定，即将腐蚀速率视为一个具有常均值的随机变量，船体板的腐蚀厚度与时间呈线性关系。但近年来的研究表明，钢材腐蚀过程复杂，单一的线性模型并不能很好地描述这种行为，而采用非线性腐蚀模型更为合理。

5.1 常规腐蚀模型

Southwell 等[6]由实验观察得到，在2～5 年内曝光的金属板腐蚀厚度增量呈非线性变化，之后，呈线性增加。根据这个结论，Southwell 提出了一种金属腐蚀产物厚度d随时间T变化的双线性模型，如式(7)：

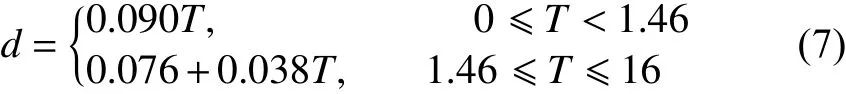
1998 年，Melchers[7]基于实验数据也给出了一种腐蚀损耗厚度线性稳态模型，拟合公式如下：

Yamamoto[8]统计了不同船舶不同部位的腐蚀情况，发现船舶板的腐蚀损耗呈现一种时间非线性特征，随后，Melchers[7]在稳态模型的基础上又提出了一种新的幂函数模型，用于模拟板壳厚度腐蚀模型，如式(9)：

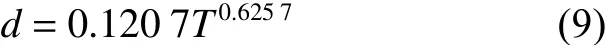
参考之前的研究数据，Soares 等[9]提出了一种非线性指数腐蚀模型（以下图中称GC 模型），主要用于描述船舶板架的腐蚀进程。其将整个腐蚀过程分为了3 个阶段，如图6 所示。

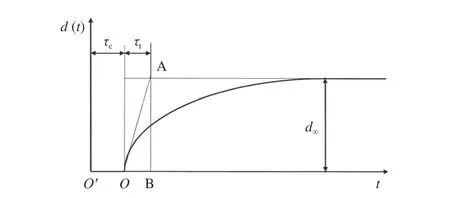
图 6 Soares 等[9]提出的腐蚀模型Fig. 6 Corrosion model proposed by Soares,et al[9]

5.2 一种新型腐蚀模型

Southwell 线 性 模 型、Melchers 稳 态 模 型及Yamamoto 幂函数模型均未考虑腐蚀防护层（CPS），而Soares 等[9]所提模型则考虑到了腐蚀防护层的影响，然而，这些模型均忽略了下述问题：

1） Soares 等[9]提出的腐蚀模型虽然考虑了腐蚀防护层的影响，但该模型认为当腐蚀防护层失效时腐蚀才开始进行。事实上，腐蚀防护层是个渐进失效的过程，即在腐蚀防护层完全失效前腐蚀就已经开始了。

2） 在腐蚀防护层失效后，随着腐蚀层逐渐加厚和滋生微生物数量的增加，腐蚀速率最后会逐渐下降。因此，整个腐蚀过程可分为3 个阶段：无腐蚀阶段→腐蚀加速阶段→腐蚀减缓阶段。可见，上述腐蚀模型均不符合实际情况。

秦胜平等[10]依据实际腐蚀过程，将整个腐蚀过程分成了3 个阶段：1）无腐蚀阶段[0，Tst]；2）腐蚀加速阶段[Tst，TA]；3）腐蚀减缓阶段[TA，TL]。其中，Tst为腐蚀开始时间，TA为腐蚀加速寿命，TL为结构使用寿命。

Yamamoto 等[11]和Paik 等[12]发现，实际腐蚀速率的概率密度分布可以假设成服从Weibull 分布，而Weibull 分布的概率密度函数曲线与秦胜平等[10]所提腐蚀过程的3 个阶段也相契合，故考虑新的腐蚀速率模型时用Weibull 分布形式表现。腐蚀速率模型如式（13）所示。

5.3 新型腐蚀模型合理性验证

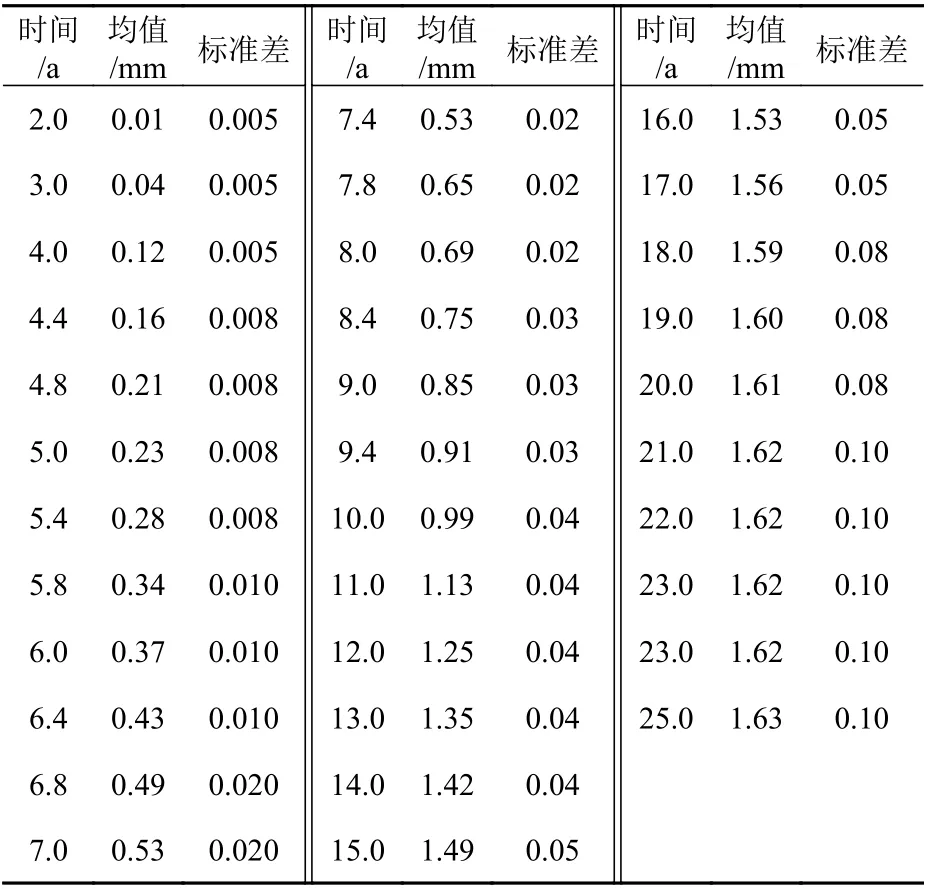
表4 Paik 等[12]提供的能够散货船的腐蚀数据Table 4 Corrosion data of a bulk carrier provided by Paik et al[12]

由图7、图8 可知，新型腐蚀模型将整个腐蚀过程分成了3 个阶段（无腐蚀阶段→腐蚀加速阶段→腐蚀减缓过程），符合结构的实际腐蚀过程。虽然Paik 等[12]提供的腐蚀数据不是铝合金船的，但相比其余4 种通用材料腐蚀模型而言，该新型腐蚀模型的拟合性显然最好。

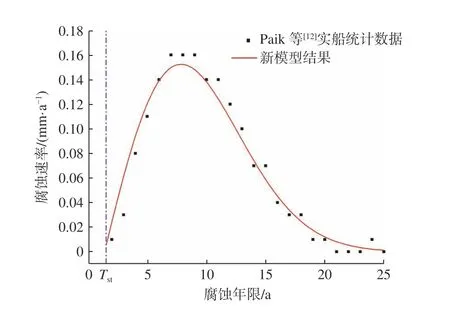
图 7 腐蚀速率模型结果与试验结果对比Fig. 7 Comparison of corrosion rate model results and test results

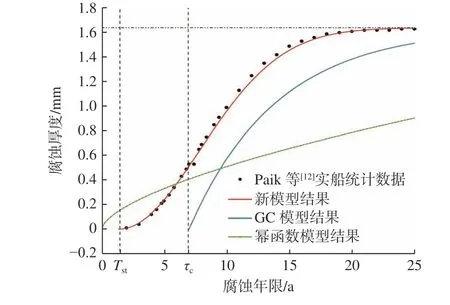
图 8 腐蚀厚度模型结果与试验结果对比Fig. 8 Comparison of corrosion thickness model results and test results

5.4 基 于 不 同 腐 蚀 模 型 的 热 点 疲 劳 特 性分析

对于新型腐蚀模型，可以发现，当β 的取值不同时，腐蚀模型的形状也不同，即该模型具备一定的灵活性。建立不同的β 值所对应的腐蚀速率模型如图9 所示。

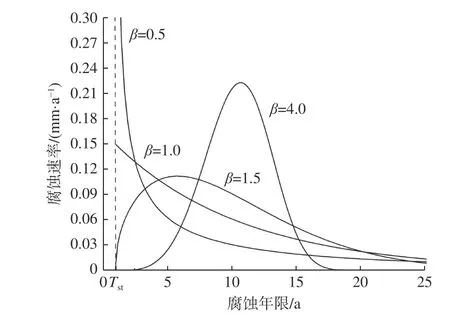
图 9 新腐蚀模型的灵活性Fig. 9 Flexibility of the new corrosion model

根据120 m 铝合金三体船的设计要求，其服役寿命为25 年，船体外板的腐蚀极限厚度d∞=1.5 mm，腐蚀防护层寿命5 年。由于内部结构不直接与海水接触，内、外部结构的腐蚀速率不同，故本文只研究外部热点（S1，S2，S4，S5）的腐蚀问题。

基于不同的腐蚀模型在有限元模型中进行腐蚀折减，求解三体船新的应力响应值，然后基于谱分析法对三体船进行在不同腐蚀年限下的疲劳寿命评估。外部热点在不同腐蚀模型下的疲劳损伤度计算结果如图10～图13 所示，无腐蚀和25 年腐蚀年限下的疲劳寿命减小率如表5、表6 所示。

由图9 可以看出，新型腐蚀模型有着较好的适应性，可以将常规腐蚀模型看成新腐蚀模型的特例。当β= 0.625 7，η=1，d∞=0.120 7 mm，Tst=0时，新型腐蚀模型可以变成幂函数模型；当β=1时，新型腐蚀模型可以变成Soares 等[9]所提模型。

根据图10～图13 的计算结果，可得不同腐蚀模型在不同腐蚀年限下对铝合金三体船热点疲劳的影响程度不同。在腐蚀的前10 年，各腐蚀模型对铝合金三体船热点的疲劳影响差距较小；在腐蚀15 年之后，双线性模型和幂函数模型相较于其他模型对热点疲劳的影响较小，而稳态模型则出现了腐蚀跳跃现象，对热点疲劳的影响较大；Soares等[9]所提模型和新型腐蚀模型在腐蚀15 年后对热点疲劳的影响差距不大，热点疲劳损伤度的平均差值仅为0.8%。

图 10 热点S1 在不同腐蚀模型下的疲劳损伤度Fig. 10 Fatigue damage of S1 in different corrosion models

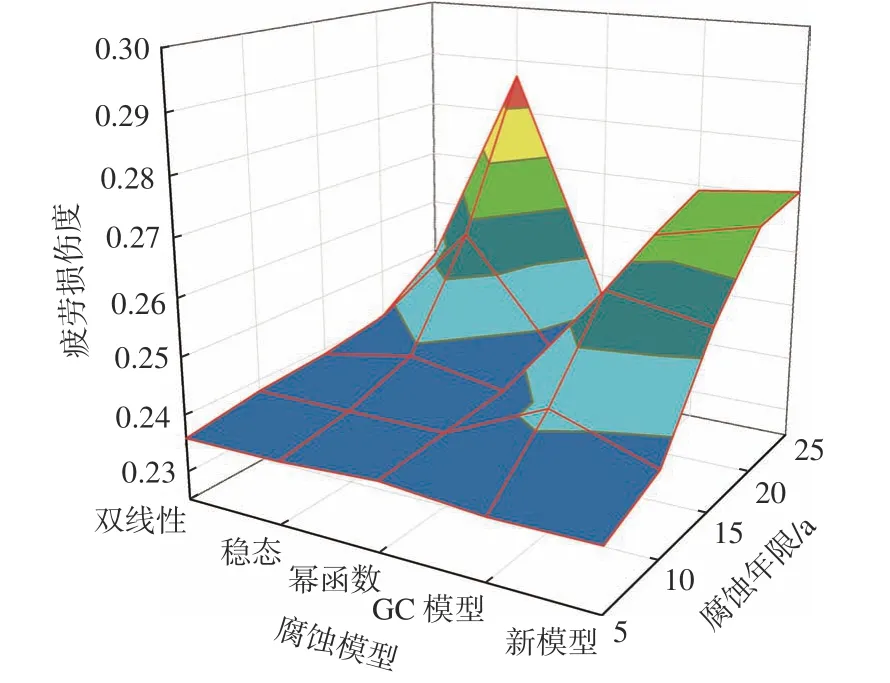
图 11 热点S2 在不同腐蚀模型下的疲劳损伤度Fig. 11 Fatigue damage of S2 in different corrosion models

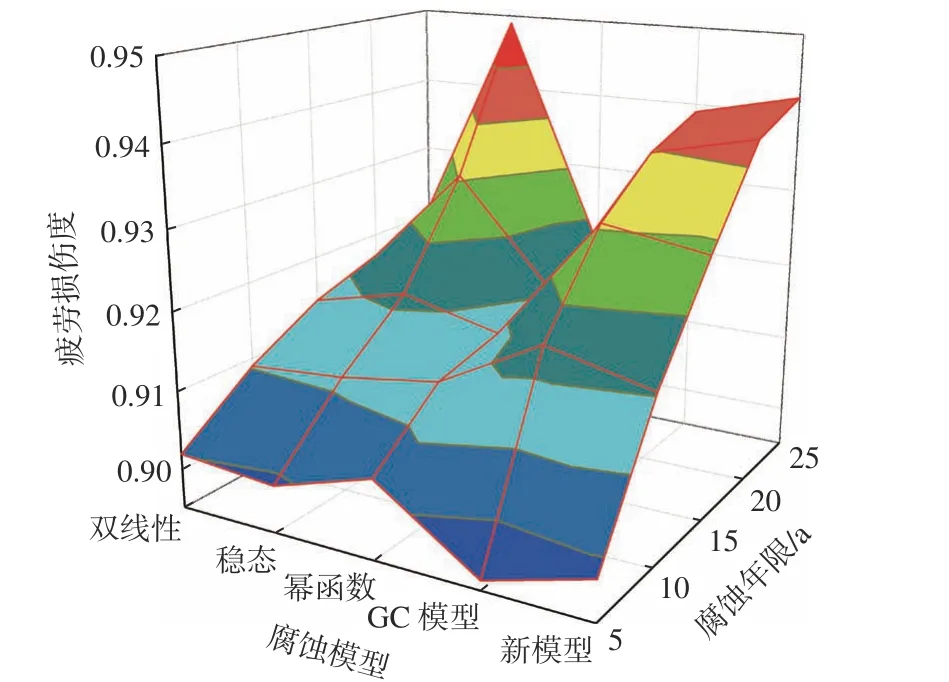
图 12 热点S4 在不同腐蚀模型下的疲劳损伤度Fig. 12 Fatigue damage of S4 in different corrosion models

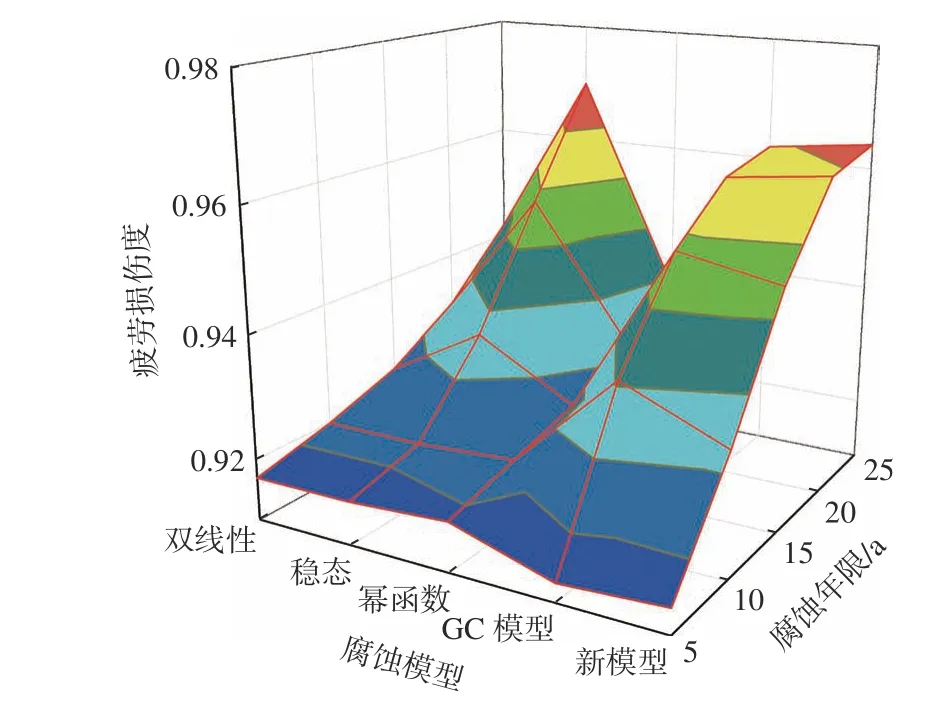
图13 热点S5 在不同腐蚀模型下的疲劳损伤度Fig. 13 Fatigue damage of S5 in different corrosion models

由表5 和表6 可以看出，在腐蚀的作用下，三体船外部热点的累计损伤度增大，疲劳寿命减小。比较4 处热点部位的结果发现，无论采用何种腐蚀模型，连接桥与主、侧体连接处（S4，S5）的寿命减少率均最小。此外，由图10～图13 所示的铝合金三体船热点处单位腐蚀厚度下的疲劳损伤度增加值(S1，S2，S4，S5 处的疲劳损伤度增加值分别为0.033，0.031，0.020，0.023 ↑/mm)，可知铝合金三体船连接桥与主、侧体连接处的抗腐蚀疲劳能力较强。

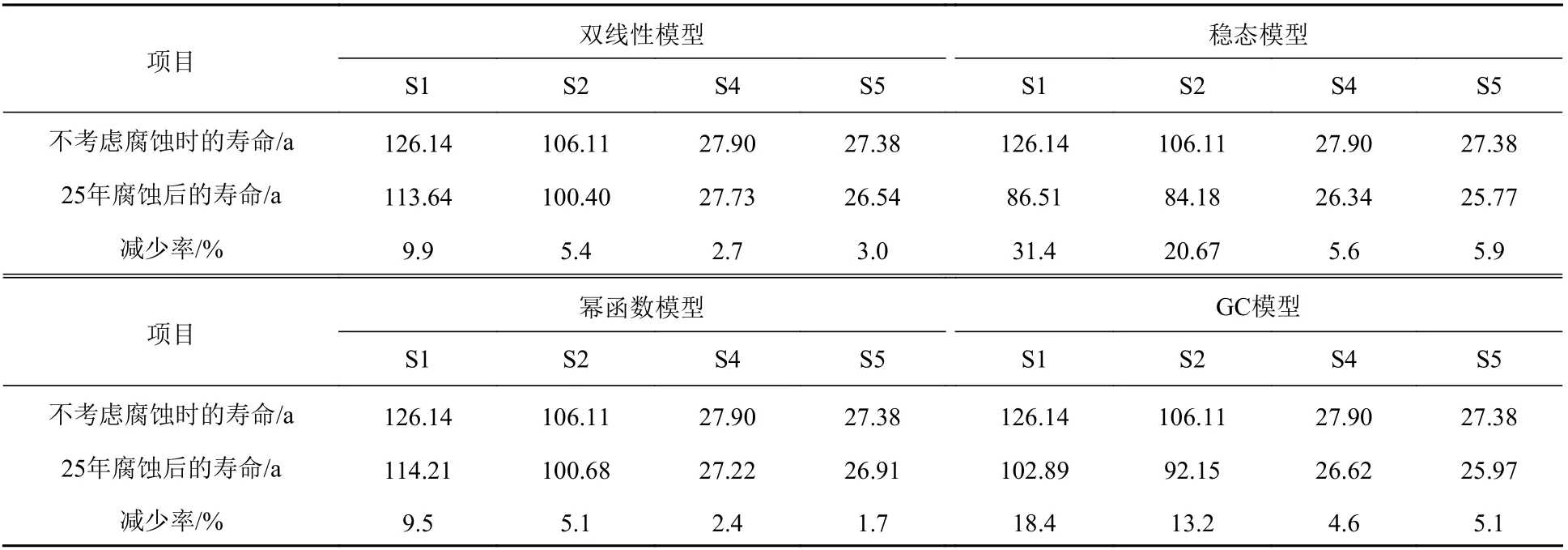
表5 常规腐蚀模型疲劳寿命降低比例Table 5 Reduction ratio of fatigue life of conventional corrosion models

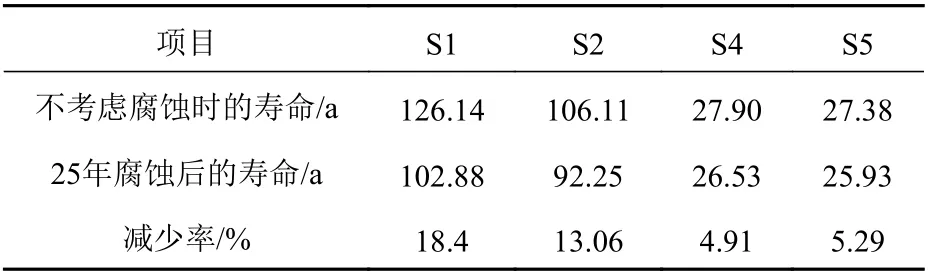
表6 新腐蚀模型疲劳寿命降低比例Table 6 Reduction ratio of fatigue life of new corrosion model

6 结 论

本文基于谱分析法，对腐蚀影响下的铝合金三体船热点部位进行了疲劳强度评估，通过研究不同腐蚀模型下的铝合金三体船热点疲劳特性，可得到以下主要结论：

1) 疲劳热点的选取应按照应力云图中的最大应力点选取，三体船连接桥部位为疲劳评估的重点对象，在进行结构设计时需特别注意。

2) 新型腐蚀模型更符合结构实际的腐蚀过程（无腐蚀阶段→腐蚀加速阶段→腐蚀减缓过程），且具有较好的适应性，可将常规腐蚀模型看成是新腐蚀模型的特例。不同腐蚀模型对热点部位的影响程度与腐蚀年限有关。

3) 不考虑腐蚀环境对船舶的影响，船舶疲劳强度评估偏危险。腐蚀对铝合金三体船不同热点部位的疲劳影响程度不同，连接桥与主、侧体连接处的抗腐蚀疲劳强度能力较强。