破冰船连续破冰的冰阻力预报
陈锐,黄武刚,陈晓璐,康美泽
中国舰船研究设计中心,湖北 武汉 430064
0 引 言
南、北极地理位置特殊,且拥有丰富的资源。开发极地航道和极地资源,开展极地科学考察具有重要的战略意义。随着全球变暖,北冰洋海冰融化,北极地区蕴藏的丰富资源和极具价值的航道,也日益成为世界各国关注的焦点。极地科学考察破冰船是探索两极的必要装备,如何准确评估极地科学考察破冰船连续破冰的冰阻力和破冰能力,是破冰船总体设计的关键技术之一,具有重要的理论和现实意义[1-2]。
在破冰船的冰阻力研究过程中,学者们采用了多种研究手段。国外早期基于模型试验、理论分析和实船观测等方法,初步建立了一些破冰船冰阻力的经验计算公式,如Lindqvist 公式[3]、Vance 公式[4]、Lewis 公式[5]、改进的Edwards 公式[6]和Riska 公式[7]等,具有较高的实用意义,其中Lindqvist 公式使用最为广泛。近年来,部分学者开始使用数值模拟方法研究船与冰的相互作用,离散元方法(DEM)与有限元方法(FEM)为应用最为广泛的2 种数值方法。DEM 注重不同离散单元间的连接方式,Zhan 等[8]采用了离散元软件DECICE 模拟了船舶在浮冰区的操纵运动,季顺迎等[9]研究了海洋结构物所受冰载荷的离散元算法并开发了Ice DEM 软件等。国内在FEM 方面的研究也逐渐兴起,王峰等[10-11]使用有限元软件LS-DYNA 对连续破冰的过程进行了数值模拟,何菲菲[12]采用商业软件DYTRAN 对破冰船的破冰能力进行了研究。冰池模型阻力试验是验证破冰阻力的重要方法,但投资成本大,试验周期长。目前,国外具备冰池试验条件的有芬兰阿克北极、德国汉堡船池,国内具备条件的有天津大学。
在极地破冰考察船的设计过程中,需要对设计船型方案的破冰阻力和破冰能力进行评价。本文将采用经验公式法和数值模拟法进行计算和结果比对,在天津大学冰水池开展模型试验以验证以上结果,并对经验公式和数值模拟计算方法的适用性和结果特点进行研究,以便为快速评价破冰船的冰阻力提供可用的方法,为进一步优化改进破冰船船型提供有效的设计手段。
1 破冰船破冰能力估算方法
1.1 常用破冰阻力估算方法
冰阻力是破冰船舶在冰区行进过程中所受的主要载荷,对船舶的破冰阻力有着直接影响。研究人员基于实船测试以及理论分析,从不同角度推出了包括Vance 公式、Lindqvist 公式、Lewis 公式、Su 公式和Riska 公式在内的一系列破冰阻力计算公式。
本文将采用Lindqvist,Vance 和Lewis 这3 种经验公式进行计算,探究不同经验公式对冰阻力预报存在的差异,并对经验公式进行参数敏感性分析。经验公式预报结果也用于后文与数值模拟结果以及船模试验结果进行比对分析。
1.2 平整冰破冰阻力试算结果及分析
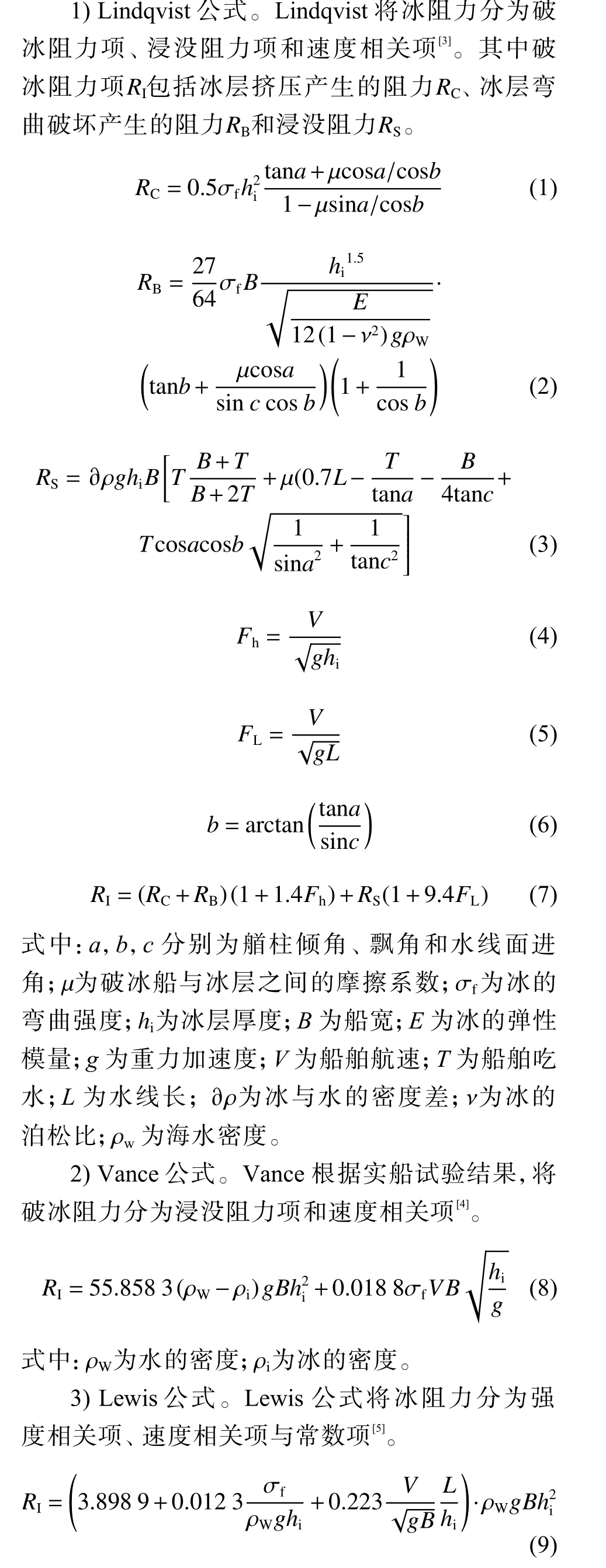
经验公式所需参数如表1 所示。针对不同的航速与海冰厚度,采用经验公式对冰阻力进行了计算,具体工况与计算结果如表2 所示。对于3 种冰厚(1.5,2 及2.5 m),选取1~4 kn 不同航速,用3 种经验公式进行冰阻力计算,如图1 所示,对于不同的工况,各经验公式所得的计算结果都表明,冰阻力随着船舶航速与冰厚的增加而增大,但具体数值存在差异。
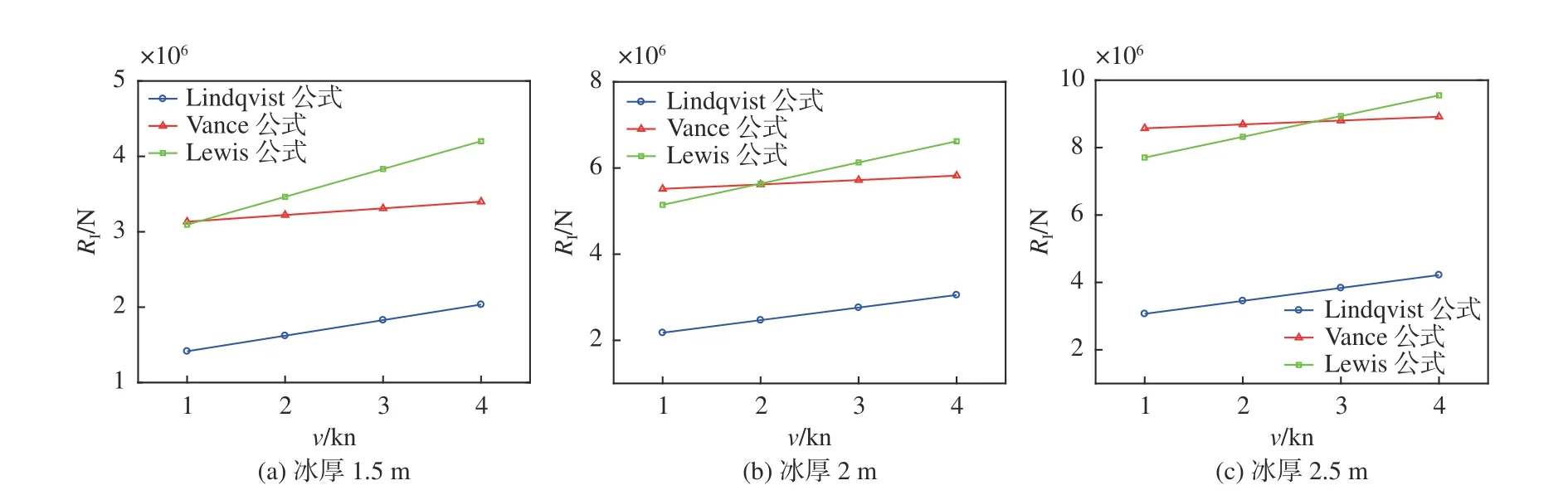
图1 不同工况下经验公式预报冰阻力的比较Fig. 1 Comparison of the results obtained with empirical formula under different conditions
冰阻力的大小与破冰过程中船舶、冰层的参数大小密切相关。参数敏感性分析是将每个自变量分别在一定范围内变化,根据其相应的变化趋势以及变化程度,评估其变化量对结果的影响大小,参数敏感性分析即为对影响程度大小的衡量[11]。敏感性系数越大,则自变量对结果的影响也越大。根据表1 所示的经验公式计算所需参数,选取了航速、冰厚以及弯曲强度3 个变量,针对航速为2 kn,冰厚1.5 m,船宽26 m,弯曲强度900 kPa 的初始条件,进行参数敏感性分析,结果如图2 所示。
图2 参数敏感性分析Fig. 2 Parameter sensitivity analysis
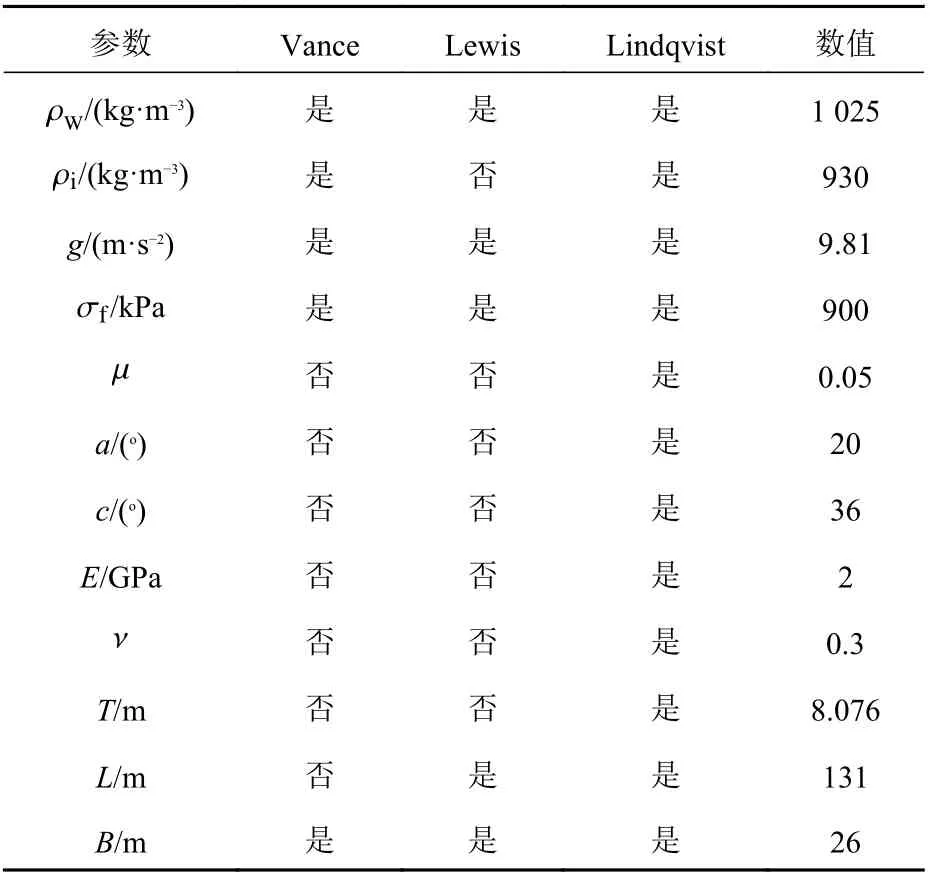
表1 经验公式计算所需参数Table 1 Main parameters required by calculation of ice resistance formulas
从图中可以看出,若船舶航速增大25%,Lindqvist,Vance 和Lewis 公式对冰阻力的预报结果分别增大了10.15%,2.60%以及8.78%。航速的变化对Lindqvist 预报的冰阻力变化率影响最大,对Vance 公式的影响最小。冰厚的变化对3 种经验公式的预报值均有较大影响,若冰厚增大25%,Lindqvist,Vance 和Lewis 公式对冰阻力的预报结果分别增大了39.83%,54.63%以及47.60%。冰的弯曲强度对Lindqvist 预报的冰阻力变化率影响最大,若弯曲强度增大20%,Lindqvist 预报结果增大13.96%,Vance 和Lewis 公式增长不大,增长率均在3%以内。
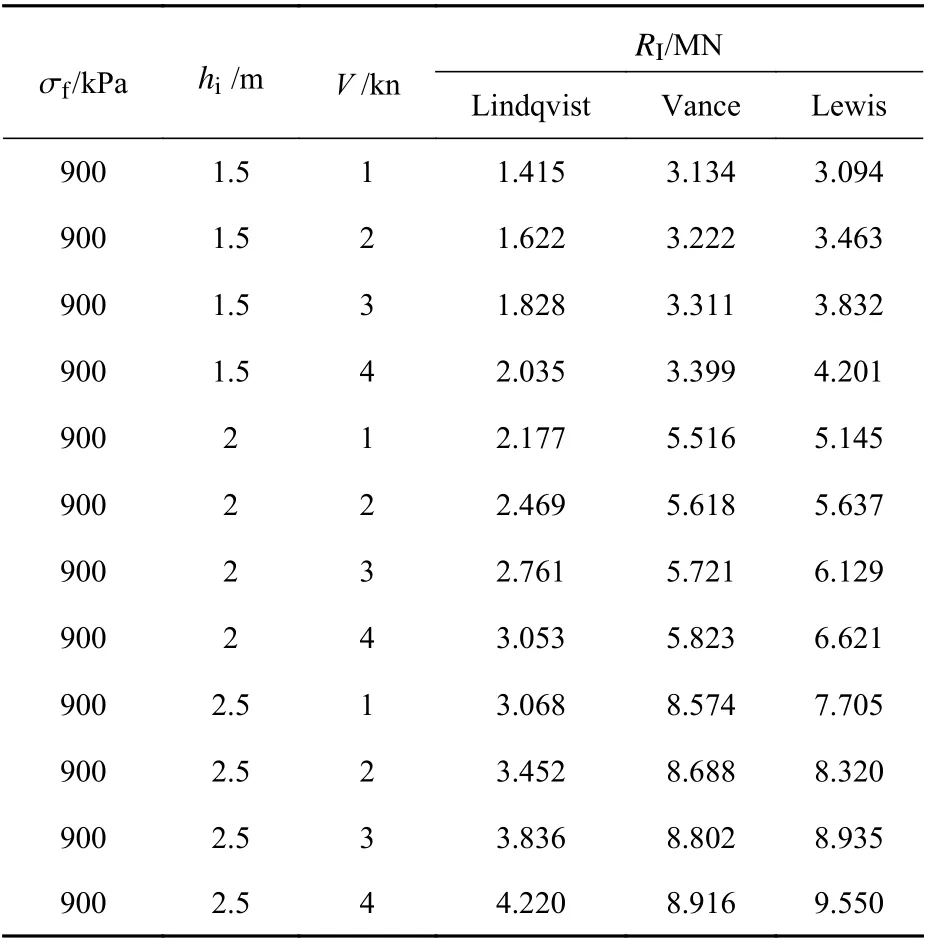
表2 经验公式计算结果Table 2 Results of ice resistance formulas calculation
2 破冰船冰阻力的数值模拟
本节在ANSYS 经典模块中进行船模与冰层建模与网格划分。采用非线性有限元软件DYNA,基于传统有限元方法与黏聚单元法(ICEM)构造冰层数值模拟模型,对破冰船在平整冰区航行时连续破冰过程中的破冰阻力进行了数值模拟。
数值模拟工况参考委托天津大学建筑工程学院对某船舶开展的阻力模型试验,采用缩尺比λ为30 的船模,对不同冰厚与航速下船模的破冰阻力进行数值模拟,以便与船模试验结果进行比对分析。船模的主要尺度如表3 所示,其中La为总长,Bw为水线宽, ∆为排水量,模拟工况如表4 所示。
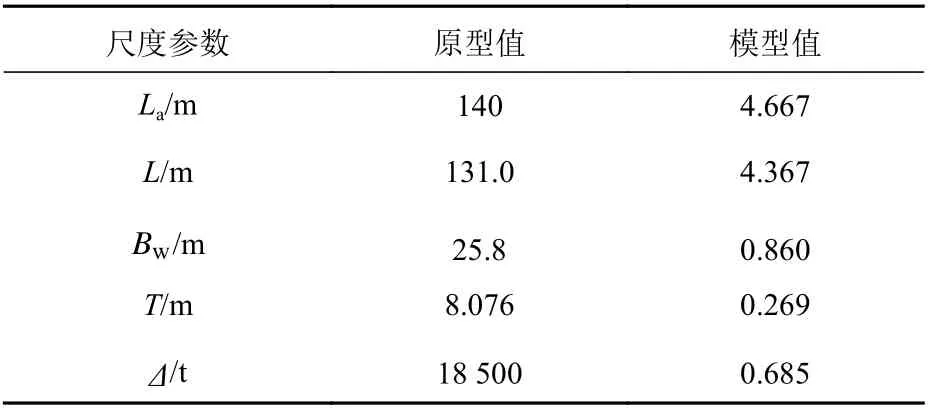
表3 船模的主要尺度Table 3 Main dimensions of the ship model
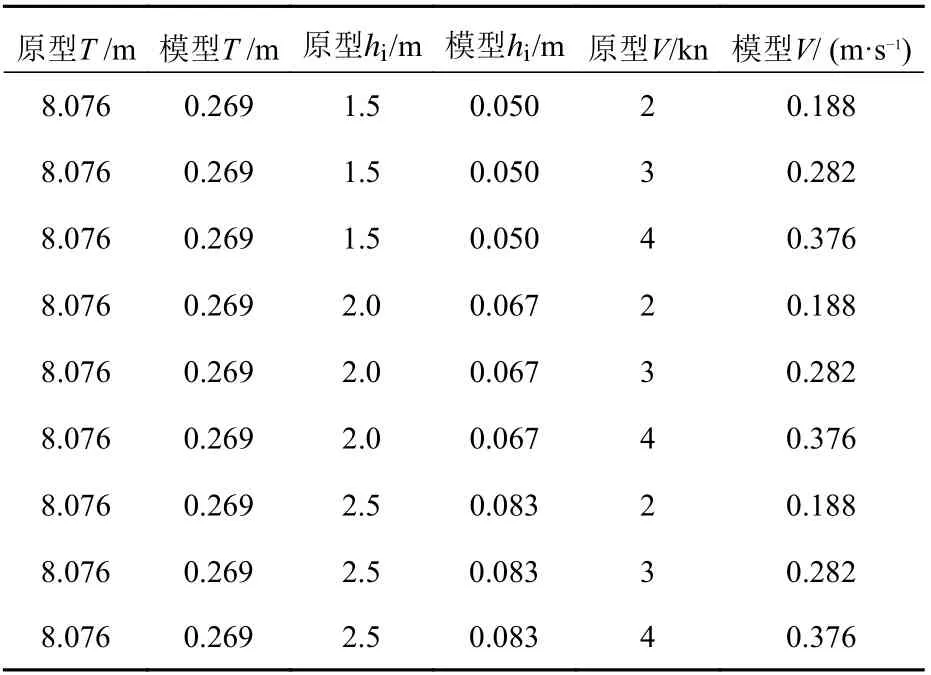
表4 数值模拟工况Table 4 Different simulation conditions
2.1 基 于 传 统 有 限 元 法 的 破 冰 阻 力 数 值模拟
有限元数值模拟技术发展迅速,显式动力学有限元软件DYNA 被广泛应用于解决碰撞接触问题,本文在应用LS-DYNA 时,连续体的处理方法采用Lagrange 法[13]。
数值模型如图3 所示,平整冰长9 m,约为2 倍船长,宽度为4.5 m,约为5 倍船宽,在平整冰竖直方向上仅设置一层网格来模拟平整冰的弯曲断裂。在不与船壳接触的三边界上采用三边固支对冰层进行约束。在船冰碰撞的数值模型中,船体定义为壳单元,冰单元定义为实体单元。船网格采用四边形面网格划分,在碰撞过程中,不考虑船壳变形,故采用刚性材料MAT020-RIGID。由于冰材料的结构特性非常复杂,被视为一种材料属性和本构关系都十分复杂的材料,国内外学者在数值模拟研究中都没有得出较理想的研究成果[14]。本文在参考国内外多位学者的研究后,采用各向同性弹性断裂失效本构模型模拟冰材料[14-15],模型参数的选取如表5 所示。其中, ρ为密度,SM为剪切模量,SIGY为屈服应力,ETAN为塑性硬化模量,BULK为体积模量,EPF为塑性失效应变,PRF为截断压力。

图3 船模和平整冰的网格划分Fig. 3 Mesh patterns of the model and level ice
速度为0.188 m/s,冰厚为0.05 m 时,破冰船在连续破冰过程中所受冰阻力的时历曲线如图4 所示。从图中可以看出,在0~3 s 阶段,船体不断挤压冰单元,由于船冰接触面积的不断增大,冰阻力曲线随时间的增长振荡上升。大约在3 s 之后,由于船艏完全进入冰层,单位时间内破冰船挤压侵蚀的冰单元趋于稳定,故冰阻力的均值亦趋于稳定状态。而在碰撞过程中,由于冰单元的失效,会出现接触力卸载现象,故冰阻力会呈现振荡状态。
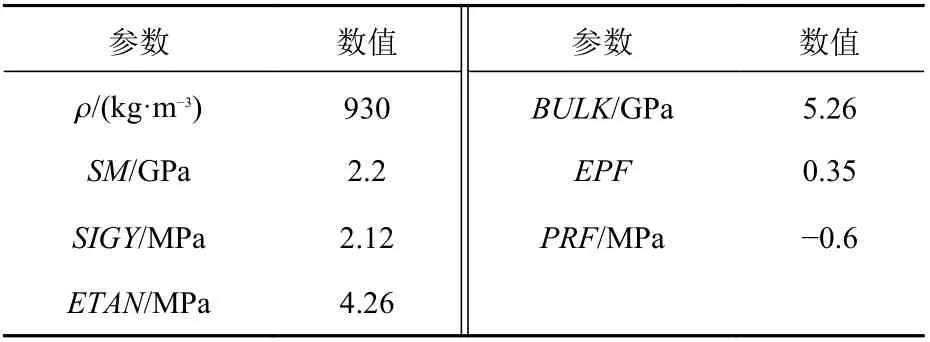
表5 冰体材料参数Table 5 Material parameters of the ice

图4 冰阻力时历曲线Fig. 4 Time history of ice resistance
2.2 基于黏聚单元法的破冰阻力数值模拟
黏聚单元模型以断裂力学为理论基础,广泛应用于固体材料裂纹的形成、增长与稳定分析。将黏聚单元应用于冰层的数值模型的建立,可模拟平整冰与破冰船相互作用时发生的弯曲断裂以及大裂纹的随机扩展过程[16-17]。
不同于传统有限元模型中用标准六面体单元直接相连建立冰层,黏聚单元法将实体冰单元进行离散,离散后的各个实体冰单元的内边界上插入共节点的零厚度黏聚单元,通过黏聚单元将相邻的实体冰单元进行连接。2 种单元相互独立且具有不同的材料属性,又相互连接传递受力。其中,实体冰单元根据冰材料的本构关系发生弹性和塑性变形。黏聚单元是潜在的断裂平面,当黏聚单元承受的强度超出临界断裂强度时,黏聚单元失效,实体单元间出现缝隙而脱落破碎[11]。黏聚单元法所建立的冰层模型如图5 所示。图5(a)为平整冰模型,白色纵横交替的为黏聚单元,蓝色为实体冰单元;图5(b)为平整冰模型的局部放大图,蓝色为实体冰单元。


图5 黏聚单元法建立的冰层模型Fig. 5 Level ice model constructed by cohesive element method
船壳采用刚性材料MAT020-RIGID。对于实体冰单元可以采用许多简化的不同材料进行模拟,例如:各向同性弹性模型、简化的破损模型、弹塑性模型等。本文主要考虑冰材料的弹性与塑性,实体冰单元采用MAT012-ISOTROPIC-ELASTICPLASTIC。黏聚单元采用MAT186-COHESIVEGENERAL 材料,具体各个部分材料参数如表6所示[10,16],表中G为杨氏模量,PR为泊松比,S为屈服应力,ETAN为塑性模量,TS为拉伸强度,SS为剪切强度,En为 法向断裂能量释放率,Es为剪切断裂能量释放率
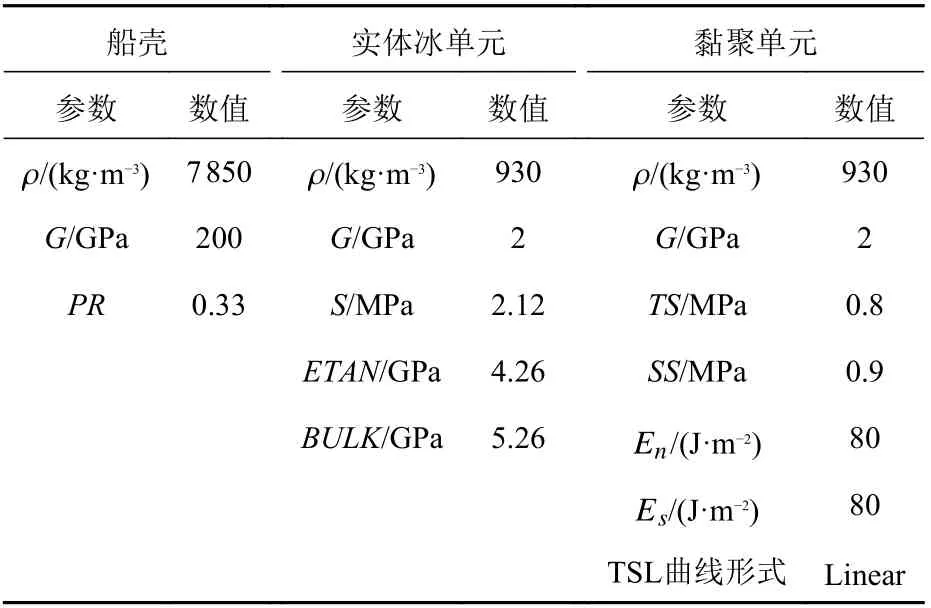
表6 材料参数Table 6 Material parameters of the ship shell and ice
以冰厚为0.067 m,3 个不同航速下的工况的数值模拟结果为例。如图7 所示,取冰阻力稳定后的2 s 左右时间段内的平均值作为数值模拟的船模所受冰阻力大小。对以上9 个工况的冰阻力进行数值模拟计算。从图中可以看到,在连续破冰的过程中,经过一段时间后,模拟所得的冰阻力始终在一定范围内波动,取这一稳定区间的平均值为该工况下的冰阻力大小。可以看到,在同一冰厚下,数值模拟所得冰阻力的大小随航速增大而增加。
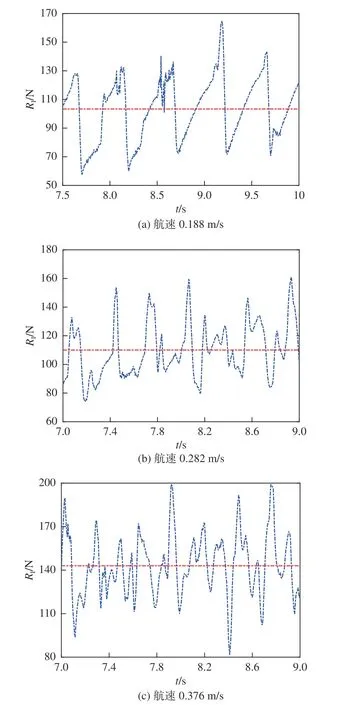
图7 冰厚0.067 m 下的数值模拟Fig. 7 Numerical simulations with 0.067 m ice thickness
3 破冰船冰阻力模型试验
3.1 试验模型与环境条件模拟
不论是破冰船的初步设计还是对其水动力性能的研究,冰水池的船模试验都至关重要,船模试验能够最为真实和准确地反映航行过程中的受力状态[18]。本文中的破冰船的船模试验在天津大学低温水池实验室开展,试验模型与数值模拟模型参数一致,具体尺度如表3 所示。
天津大学低温水池实验室在模型试验中采用第2 代模型冰——尿素冰,这种冰模型采用“喷雾引晶”技术模拟天然海冰生长过程,与天然海冰具有完全一致的分层纹理结构,表层为细小、紧密的粒状结晶层,下层为垂向分布的柱状结晶层,粒状层与柱状层的耦合关系与天然海冰保持一致。模拟环境条件断面与天然结构对比如图8 所示。

图8 模拟环境条件断面与天然结构对比图Fig. 8 Comparison of the simulation condition and realistic condition
试验中利用高精度的图像采集设备对作用过程进行水上与水下的同步实时记录,以实现对破坏模式、断裂长度的变化及运动进程进行精确的观测。冰阻力模型试验简图如图9 所示。

图9 冰阻力模型试验Fig. 9 Model test in the towing tank
3.2 试验结果与分析
以船模试验结果为基准,对经验公式法以及数值模拟结果进行了比对分析。由于文中采用的3 种经验公式中的参数为实船试验所得结果[19],在以往的文献中均用于实船冰阻力预报,故本文对比分析的结果均为外推至实船尺度的冰阻力值大小。详细数据如表7 所示。
以船模试验结果为基准,图10 为经验公式法、FEM、ICEM 与船模试验所得冰阻力结果的对比图。从图中可以看出,Vance 与Lewis 这2 种经验公式对冰阻力结果的预报非常保守,误差在47%以上。Lindqvist 预报结果较好,与数值方法所得结果接近,且误差均在30%以内。Lindqvist公式、船模试验法以及数值模拟方法所得冰阻力大小均随航速与与冰厚的增加呈上升趋势。
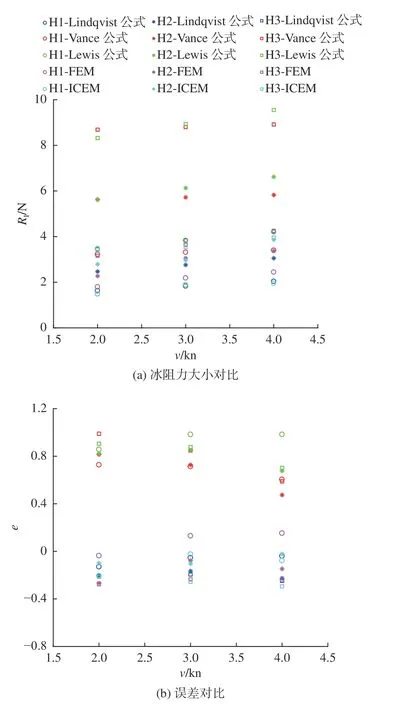
图10 不同方法所得结果的对比图Fig. 10 Comparison of the error based on different methods
对于数值方法而言,FEM 与ICEM 在厚度较小的情况下,冰阻力预报结果更准确,在冰厚较大(如2.5 m)时,误差较大在25% 左右。在冰厚较小航速较高的情况下,如1.5 和2 m 时,ICEM方法预报的冰阻力值较传统有限元法更为准确,与船模试验结果相比精度误差在10%以内。

表7 各方法所得冰阻力汇总Table 7 Results of ice forces obtained by different methods
4 结 论
本文采用经验公式法、数值模拟法以及船模试验法对破冰船在平整冰中连续航行时的冰阻力进行了预报。数值模拟法中分别采用传统有限元方法与黏聚单元法构建冰层,以船模试验结果为基准,对比分析了数值模拟结果以及经验公式法所得冰阻力预报结果。为了能够最为真实和准确地反映航行过程中的受力状态,本文中的破冰船的船模试验在天津大学低温水池实验室开展。得出结论如下:
1) 冰阻力随航速、船宽、冰厚以及弯曲强度4 个变量的增大均呈上升趋势,其中冰厚对冰阻力的影响最大。3 种经验公式中,Lindqvist 公式的预报结果与船模试验结果更为接近,而Vance和Lewis 公式更为保守。
2) 数值模拟法可以较为准确地进行冰阻力预报,预报值与船模试验结果较为吻合。在冰厚为1.5 m 时可以采用传统有限元法对冰阻力进行预报,其预报结果精度在可接受范围内且结果偏保守,适于工程应用。在冰厚为2 m 时,可以采用黏聚单元法,因为其预报精度最高,在3 种航速下误差均在10%以内。
本文验证了数值模拟法和经验与解析公式预报的适用性和准确性。说明采用传统有限元法与黏聚单元法构造冰层数值模拟模型对破冰过程中的冰阻力预报较为可靠,且文中选取的冰材料参数也与实际参数相对符合,可用于后续的工程应用。在实际的冰阻力预报中,可以结合经验公式法与数值模拟的方法,以兼顾预报结果的准确性与高效性。

