近场动力学在冰区船舶与海洋结构物中的应用进展与展望

薛彦卓，刘仁伟，王庆，倪宝玉

哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001

0 引 言

随着冰区航行的日益频繁，冰与海洋结构物的碰撞事故急剧上升[1-2]，对冰区海洋结构物安全问题的研究就显得非常重要。在研究层冰破坏的问题上，基于经典连续介质力学的有限元方法是采用偏微分方程来求解运动方程，要求运动方程在求解域处连续可导。然而，这与裂纹破坏处不存在偏导数相矛盾，若要求在裂纹处重新划分网格并预先估计裂纹扩展的方向与速度，又导致在模拟裂纹自发地生长扩展以及在求解复杂载荷条件下冰层运动的破坏时面临很多困难。鉴于此，Belytschko 等[3-4]提出了扩展有限元法，通过引入辅助方程来解决因不连续问题而导致偏微分方程不存在的问题。然而，对于复杂的非线性问题和三维问题，辅助方程的应用变得较为困难。内聚力模型[5]是另一种研究裂纹扩展的方法，其通过在界面处引入张力位移函数来判定是否发生开裂。但是，在应用内聚力模型时，需要预先知道裂纹扩展的路径，同时还要受到单元离散问题的制约，可见，采用此方法解决破坏断裂问题仍面临很多挑战。

对于无网格法而言，例如离散元法[6-7]（discrete element method，DEM）、光滑粒子流体动力学法[8-9]（smoothed particle hydrodynamics，SPH）等，由于它们是将连续体离散为能够描述连续体的变形信息和材料信息的有限节点，通过构造插值函数来离散控制方程，因此不需要重新生成计算网格及考虑网格畸变等问题，兼具了拉格朗日和欧拉方法的优点。但是，这些方法在计算细微观缺陷发展、三维断裂、群裂纹等复杂问题方面仍面临很大的挑战。至于其他数值方法，例如原子模型理论，是通过非局部理论来描述裂纹和破坏的，该理论认为裂纹的产生是因原子间的键断裂所致。受限于计算效率，其与其他数值方法耦合是一个必要的途径，可便于求解宏观尺度的工程问题。然而，在将这些数值方法耦合成多尺度模型时，不同模型之间力的转换关系却相当复杂。

为解决上述问题，Silling[10]于2000 年提出了一种新的连续介质力学公式——近场动力学。近场动力学的控制方程是积分−微分方程，不包含空间导数，这使得该理论对于研究裂纹等不连续性的问题非常具有吸引力。此外，近场动力学可以看作是分子动力学的宏观连续体，这种特性使其非常适合进行材料的多尺度分析。在文献[10]中的原始公式中，其假设材料点之间的相互作用力大小相等、彼此方向相反。尽管这一假设大大简化了计算，但也引入了一些限制，例如材料常数的局限性、无法捕捉塑性变形等。为了克服这些限制，Silling 等[11]又开发了态基近场动力学（state-based peridynamics）。为了使新模型与原模型有所区别，将原模型命名为键基近场动力学。在态基近场动力学中，相互作用力不一定始终保持大小相等且彼此方向相反。

近场动力学方法与经典连续介质力学方法最大的不同之处在于其控制方程是采用积分形式[12]，并在不连续处仍然适用。因此，在处理裂纹等不连续问题时，近场动力学方法可以“自发”模拟裂纹的产生和扩展，无需预设裂纹，在处理破坏问题上具有较大优势。同时，与离散元等非连续方法相比，近场动力学方法源于连续介质力学，具有严密的理论性。目前，近场动力学在模拟混凝土材料[13-15]、纤维复合材料[16-18]、岩石破坏[19-23]等方面已有许多成功的应用。为了更好地了解近场动力学在冰区船舶与海洋工程中的应用，本文拟对近场动力学在上述领域的应用问题进行梳理，内容主要包括冰材料本构模型、冰−结构作用模型、冰−水耦合方法、结构物力学模型、水下爆炸破冰应用及结构表面覆冰除冰的应用等。

1 近场动力学理论

近场动力学理论可以看作是连续介质形态下的分子动力学理论。其假设将连续介质体B 离散为均匀的物质点颗粒，每个物质点x都具有一个以自身为中心的球形邻域H，该球形的半径为δ，如图1 所示。该物质点只与其邻域以内的临近物质点间存在非局部力，这种非局部力称为“对点力密度”。该力密度的概念与分子动力学的“键”类似，力密度的大小和方向与键长有关，而连续体的形变会造成键长发生变化，进而改变物质点所受的力密度。对物质点的力密度进行积分，即可获得该物质点所受到的合力，采用牛顿第二定律，即可求解物质点的加速度。在参考坐标系下，物质点x的运动方程为[10,24]

图1 近场动力学与局部理论[25]Fig. 1 Peridynamics and local theory[25]

式中： ρ为材料密度；u为 物质点的位移；f为物质点之间的“对点力密度函数”，该力密度函数代表物质点x与 物质点x′之 间的非局部力作用；Hx为由物质点x的所有临近物质点构成的域；b为施加在物质点x上的体积力；Vx′为x′的体积。

1.1 冰的键基近场动力学模型

海冰作为一种工程材料，其力学性能较为复杂，且在不同的温度、应变率下的差异较大，并有明显的尺寸效应。在低应变率下海冰表现为韧性，而在高应变率下表现为脆性。在海冰与结构相互作用的过程中，冰的破碎也较为复杂，一般而言，存在于冰内部的微裂纹将在海冰内部聚集，在形成更大的裂纹后其会发生贯穿性破坏，从而导致整体冰排发生破坏。冰既会以块状形式发生弯曲或屈曲破坏，也可以挤压破坏形式从结构接触区域剥落下来形成细小的碎末。对于一个连续破冰过程，每次失效都会改变后续冰的边界条件并对海冰的破坏产生影响。采用近场动力学方法研究冰的工程问题的单位主要集中在哈尔滨工程大学[26-30]。

近场动力学力密度函数应包括以下典型的海冰力学特性：1）在快速压缩加载下表现为弹脆性；2）在低速压缩加载下表现为韧性；3）在任何速率的拉伸加载下均为弹脆性；4）拉伸强度与压缩强度不同。

在键基近场动力学模型中，力密度的表示为[24]

下面，给出常用的3 种力密度模型[26]。如图2(a)所示，对于此类弹脆性材料，近场动力学的力密度函数可以表示为

式中：t为时间；µ为判断键失效的常数。如图2(b)所示的弹韧性模型，此时近场动力学的力密度函数模型可以表示为

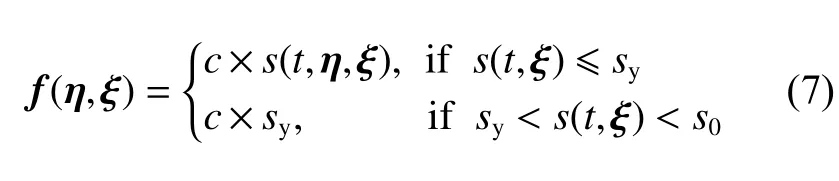
式中：s0为 键的临界伸长率；sy为键塑性变形时的伸长率。

另一种模型是考虑冰的拉压不同属性，如图2(c)所示，此时的力密度函数需要根据键变形后伸长或缩短并结合式（6）和式（7）使用。

裂纹产生时，连续体上、下两部分彻底分离，这会破坏贯穿裂纹上的所有键。键的临界伸长率s0可以根据破坏发生所需要的能量得到，其表达式为：

1.2 冰的态基近场动力学模型

态基近场动力学中引入了力状态T的概念，它是变形状态Y的映射，而映射关系为材料的本构模型。与经典力学类似，在近场动力学中，实现本构模型的前提条件是获得物质点的非局部变形梯度F。态基近场动力学是采用一种积分的方式来求解物质点的变形梯度，首先定义2 种非局部，即参考构型(未变形坐标系)下的非局部形状张量K和当前构型(变形坐标系)下的非局部张量B，其计算如下[11]：

2 冰−结构碰撞模型

冰−结构物碰撞作用中常用的接触模型按照结构是否变形，可以分为刚性接触和弹性接触2 种。刚性接触模型适用于把结构物作为刚体处理的问题，例如采用键基近场动力学方法研究的冰−桨作用[31-34]、竖直结构−冰作用[35]等。弹性接触模型适用于把结构物作为弹性处理的问题，例如采用键基近场动力学方法研究的船−冰作用[36-38]等。

2.1 刚性接触模型

在刚性接触模型的应用方面，Ye 等[31-34]采用键基近场动力学方法研究了冰−桨作用模型，如图3（各分图中，左为后缘，右为前缘）所示；Ye 等[31]首次提出了一种适用于冰−桨接触的判断算法，该算法有利于提高接触判定的准确性和计算效率；Wang 等[33]研究了不同推进速度、接触位置、螺旋桨转速和冰尺寸等参数对冰−桨碰撞过程的影响；Xiong 等[34]研究了冰−桨作用中遮蔽效应的影响，分析了前、后多桨以及单桨单个桨叶的遮蔽效应，研究发现，遮蔽效应可使船艉螺旋桨或伴随桨叶上的冰载荷减小；Ye 等[32]研究了冰−桨作用过程中冰铣削过程中螺旋桨叶片上的动压力分布，分析了颗粒间距对铣削力曲线、冰破坏及压力分布的影响。需要注意的是，以上研究中的冰均是采用弹脆性本构模型，螺旋桨被视为刚体。因此在冰−桨作用研究领域，认为未来研究的重点应是冰的本构模型（包括弹性模型、弹塑性模型等）和螺旋桨的结构响应（包括变形、振动、疲劳等）。另外，因冰−桨作用过程发生在水中，因此水的影响不可或缺，应针对水动力对剥落冰块运动的影响、剥落冰块间的碰撞作用等相关领域进行深入研究。同时，在螺旋桨几何参数、冰的特性参数以及流速等工作条件因素对冰−桨作用的影响方面，仍需深入研究。

图3 冰−桨作用过程中桨叶后缘和前缘的压力分布[32]Fig. 3 Pressure distribution on the trailing edge and leading edge of blade during propeller-ice interaction[32]

Liu 等[35,39]研究了竖直结构−平整冰（层冰）作用，模型中的海冰采用的是弹塑性材料，具有一定的屈服条件和破坏准则；其采用单自由度振动方程研究结构在作用过程中的振动特性，分析了冰的厚度、结构直径、速度等对冰力和结构振动响应的影响。结果表明，这3 个参数均与冰力和振动位移的总体水平呈现正相关。此外，根据速度系数与冰速的关系，还提出了一种用于预测振动位移的速度系数等，模拟结果如图4 所示，图中变量为粒子的损伤程度。

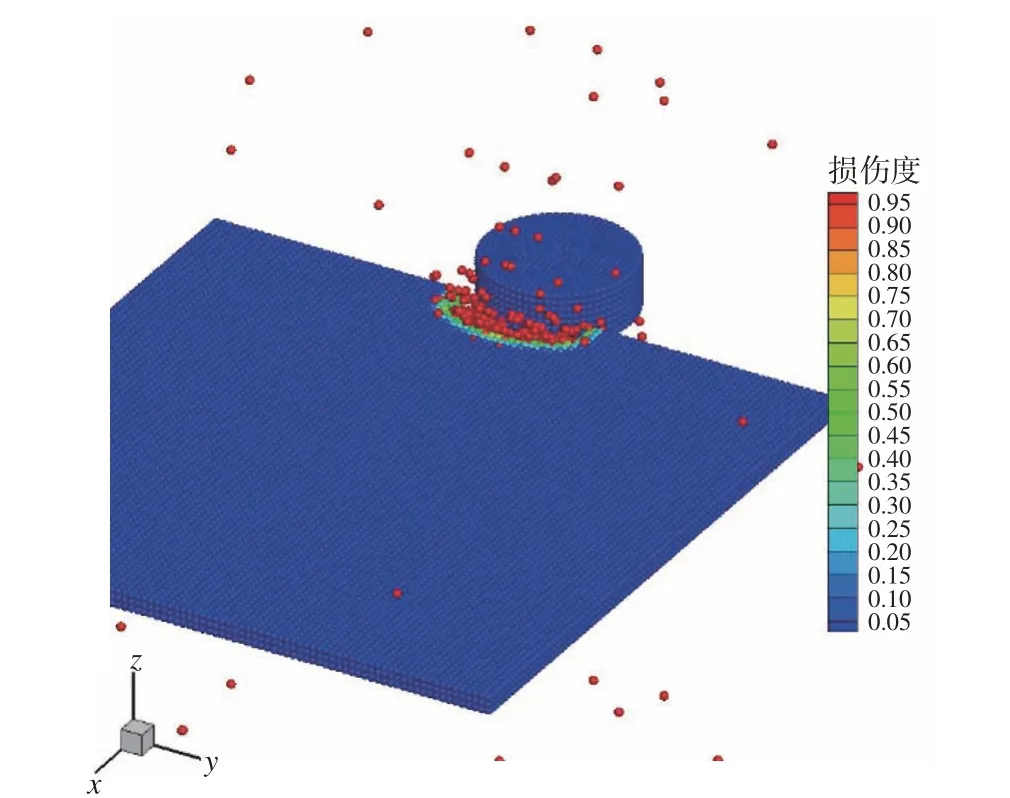
图4 竖直结构与层冰作用[36]Fig. 4 The simulation of vertical structure-level ice interaction[36]

Xiong 等[34,40]研究了冰球高速冲击破坏的过程以及冲击载荷的规律，如图5（图中，Δ为粒子间距，D为模型直径）所示。研究发现，冰球的冲击载荷随着冲击速度的增大而增大，冲击速度越大，冲击载荷时程曲线上下震荡的现象就越严重，而冲击速度越小，冰球裂解后的碎冰块尺度也越大。

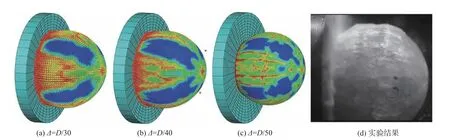
图5 不同颗粒间距冲击结果的比较[34]Fig. 5 Comparison of the impact loads with different particle spacings[34]

2.2 弹性接触模型

弹性接触模型来自美国Sandia 实验室的内部近场动力学计算平台——EMU 平台中的接触力密度模型。实现的方法是将冰−结构物模型中的物质点赋予不同的材质，当两种分属于不同材质物质点的相对位置满足一定的判定标准时，两种种物质点之间会产生排斥力的作用。根据EMU手册，当结构物中的物质点与冰的物质点不断靠近并达到一个判定距离rsh时，分属于不同材质的物质点相互排斥，此排斥力用于定义接触的两个不同物体之间的接触力。

上述模型适于将结构物作为弹性体处理的问题，例如采用键基近场动力学方法研究的船−冰作用[36-38]等。Liu 等[38]模拟了船−浮冰相互作用的过程，如图6 所示，研究了冰的材料特性、船−冰接触检测模型及浮冰生成模型，分析了浮冰大小、密集度和航行速度对冰载荷的影响，成功模拟了动态裂缝的产生和扩展，以及碎冰的滑移、旋转与堆积等行为。类似的工况在平整冰环境中的研究见文献[37]。可以发现，模拟中用的船型较为简化，虽然采用了弹性接触模型，但未涉及船−冰作用过程中船体的变形与振动等。因此，今后的研究内容应包括船体结构的响应（如变形、振动、损伤、破坏等），以及冰载荷在船体的分布规律等，从而进一步研究局部热点应力所带来的问题。

图6 船艏−浮冰作用模拟[38]Fig. 6 Simulation of bow-floating ice interaction[38]

陆锡奎[30]针对近场动力学和有限元耦合方法及其在冰载荷计算中的应用进行了研究，模拟结果如图7 所示。有限元方法虽已得到广泛的应用，但在模拟海冰复杂的破坏过程方面仍存在一定的局限性；近场动力学方法对破坏问题具有非常好的适用性，但在计算效率上远不如有限元方法。文献[30] 所提模型在冰载荷数值计算中可充分发挥近场动力学在裂纹模拟方面的优势和有限元方法在计算效率方面的优势。该模型中的接触模型因是直接由近场动力学接触模型改进而来，必然存在一定的不足，所以需要在今后的研究中进一步改进；在模拟计算中，因仅考虑了船−冰之间的接触力，没有考虑冰层内部的接触（例如脱落的碎冰与冰层之间的接触），故对模拟结果也存在一定的影响。

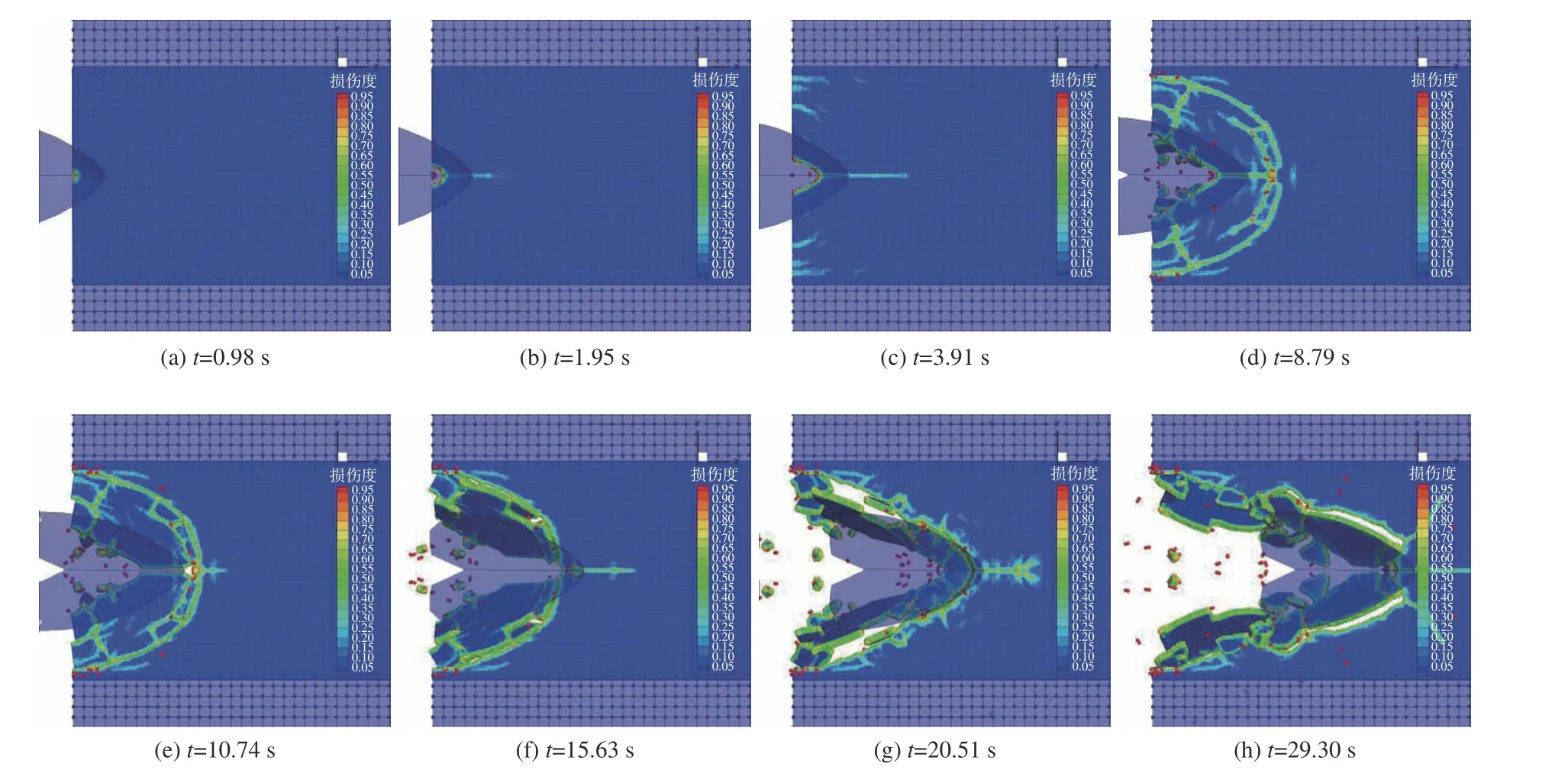
图7 近场动力学与有限元耦合方法模拟船艏与层冰作用[30]Fig. 7 Simulation of ship bow-level ice interaction using PD-FEM coupling method[30]

Liu 等[35]对冰−竖直圆柱结构的作用予以了模拟，其采用非常规态基近场动力学模型建立了冰的线弹性本构模型，建立了基于临界等效应变的材料失效准则，并采用快速傅里叶变换将力从时域转换到频域的方法研究了载荷循环特性。研究发现，冰的特征破坏频率是随结构运动速度的增加而增加的，损伤区长度保持为冰厚的0.15～0.2 倍，模拟结果如图8 所示。

图8 竖直结构−冰作用模拟[35]Fig. 8 Simulation of vertical structure-ice interaction[35]

3 冰−水耦合模型

流固耦合问题的处理方法分流固单向耦合和流固双向耦合。单向耦合方法适用于流场对固体作用后固体变形很小的情况（即流场的边界形式基本不变），而固体变形比较大时，流场的边界会随之改变，流场分布情况将有较大变化，同时存在流场对固体域应力的影响以及固体变形对流场分布的影响，在两种影响相互作用下最终达到平衡状态，所以需要进行流固双向耦合处理。流固双向耦合的求解方法有很多种，从数值计算的角度可以分为强耦合和弱耦合。其中，强耦合是将流体域、固体域和耦合作用构造在同一个控制方程中，在同一时间步内同时求解所有变量，此外，强耦合要求固体为弹性体且需要考虑由其变形引起的惯性力；而弱耦合则是把流体与固体分开，将流体域受到的载荷折算成固体域的变形，即在每一时间步内依次对流体方程和固体方程进行求解，通过中介交换固体域和流体域的计算结果来实现耦合求解[41-43]。

由于PD（peridynamics）理论的非局部特性，使得要实现流固界面数据的交换更加容易。目前，基于近场动力学方法的冰−水耦合作用均是采用双向流固耦合中的弱耦合模型。但是，因模拟流体的方法不同，求解流体作用于冰上压力的形式也有所不同，下面将分别予以介绍。

Liu 等[44]采用一种非局部耦合策略，运用耦合键基近场动力学和更新拉格朗日粒子动力学（updated Lagrangian particle hydrodynamics，ULPH）对刚体入水问题进行了研究。刚体粒子的压力pd通过其相邻流体粒子的插值来确定，如图9 所示。

图9 流体结构非局部耦合示意图[44]Fig. 9 Schematic diagram for non-local coupling of fluid structure[44]

上述工作的模拟结果如图10 所示。由于流体和固体的数值实现方法均属于非局部方法，而计算效率限制了该模型进行更大规模的应用，因此还需进行更多的工作来解决计算中的问题，例如开发自适应粒子细化以降低计算成本、开发冰碎片识别算法（碎冰的运动涉及多体多自由度模拟），以及开发更高效的模拟器等。

图10 冰板在不同时刻的损伤分布[44]Fig. 10 The damage distribution for ice plate at different times[44]

在Gao 等[45]模拟的弹性体−水作用问题中，其定义作用于ys,a处的固体粒子受到的流体作用可以用流体的压力Ps,a来 表述，如图11（图中，Vys,a为体积，bf→s为体积力，nˆ(ys,a)为法向方向，Γs,a为交界面）所示，即

图11 界面结构粒子在 ys,a处的相互作用[45]Fig. 11 Interactions of the interface structure particle at ys,a[45]

上述模型通过对弹性橡胶闸门下的溃坝进行数值模拟来验证，如图12 所示。流体和橡胶的材料属性，以及其他参数的设置参见文献[45]。该文献将PD 方法模拟结果（图12（c）显示的压力分布）与实验结果和SPH 方法获得的结果进行了对比，称该方法更容易于实现流固耦合作用的模拟，然而文中并没有具体指出与SPH 方法相比模型的优越性。

图12 实验结果、SPH 结果和PD 结果间的比较[45]Fig. 12 Comparison of results between the experiment, SPH and PD[45]

Sun 等[46]采用SPH 虚拟粒子的思想，模拟了可破坏结构−水作用，其中固体粒子的压力是由虚拟粒子（虚拟粒子对接近它们的流体粒子施加排斥力）求得，如图13 所示，公式如下：

图13 SPH 计算域中用虚拟粒子处理的边界条件[46]Fig. 13 Boundary condition treatment using repellent ghost particles in SPH computational domain[46]

针对上述模型，以可变形楔体入水为例，验证了SPH-PD 方法的准确性和有效性，如图14 所示。对于该类耦合涉及的破坏问题，首次应用了SPH-PD 方法，并从压力、粘度和损伤效应的角度对实验现象予以了解释。

图14 含损伤效应的弹性楔体入水大变形模拟案例[46]Fig. 14 Large deformation case of elastic wedge impacting on water involving damage effect[46]

上述涉及近场动力学方法的流固耦合模型中，前2 种方法中的流体是基于近场动力学的模拟，第3 种方法中的流体是采用SPH 方法模拟。因此，前2 种方法中用于求解固体粒子上受到流体粒子压力的方程具有相似性，不同之处在于第1 种方法考虑了固体粒子加速度的影响，在低速问题中两者的差别甚微，在高速等极端工况中需要加速度项来抑制非物理现象，例如固液穿透等。第3 种方法采用SPH 方法中的虚拟边界思想，建立了流固界面的数据传递。因此，关于SPH 方法固壁边界的策略或可用于类似的研究。

另一种非局部耦合策略为当固体粒子在流体粒子的近场内时，将其视为流体粒子，反之亦然。这时，需要固体粒子的相应物理量，如密度、速度和压力，才能进行流体计算，即将流体粒子假想为固体粒子[47-48]。对于态基近场动力学模型，作用于粒子的力为

4 近场动力学的应用

4.1 在海洋结构物中的应用

海洋结构在最初设计时虽然安全系数较高，但仍有可能会损坏，这些损坏可由许多原因引起，例如碰撞、爆炸、腐蚀、疲劳、过载或极端条件。结构在低温、高加载速率、多轴应力约束、钢的焊接性差等特殊条件下，会发生脆性损伤。研究海洋结构物的变形和破坏，无非是研究其组件的变形与破坏，也即梁、板、壳等结构元素或者它们之间的组合构件的力学问题。近场动力学在梁、板、壳等结构方面已有一定的研究。Chowdhury等[49]提出了一个适用于曲壳的近场动力学公式，其通过定义新的力和力矩状态场，将基于三维状态的方程简化为了面形式，并在厚度方向上进行适当积分后，从三维力状态获得了新的力和力矩状态场。Zhang 等[50]基于非线性Reissener-Mindlin壳理论建立了态基近场动力学壳模型，该模型能够模拟和预测厚壁壳结构的大变形，在数值计算中，采用应力点保证了数值的稳定性。O'Grady等[51]建立了基于态基近场动力学的梁模型，用于描述Kirchhoff-Love 板的弯曲问题。该模型是由键间旋转弹簧的概念导出，加入了各向同性弯曲状态项，以将模型扩展到适用于任意泊松比问题。

Nguyen 等[52]提出了一种新的六自由度三维壳体结构近场动力学模型，如图15 所示，并提出了基于临界能量释放率的壳体结构损伤准则，研究了壳、曲壳和加筋结构的变形，同时对裂纹扩展进行了模拟。

图15 PD 和FEM 方法模拟船用板材变形[52]Fig. 15 Simulation of deformation of ship plate using PD and FEM[52]

Gao 等[53]应用键基近场动力学建立复合板模型（该模型既考虑了变形对温度场的影响，又考虑了温度对变形的影响）预测了13 层复合材料在压力冲击载荷下的响应，并对水下爆炸作用下的复合材料层合板进行了数值分析。Nguyen 等[54]对船舶结构在损伤传播过程中的纵向强度（弯矩）进行了模拟，并比较了完整船与不同开孔尺寸船舶的纵向强度，最后给出了开孔船舶结构损伤扩展过程中的抗弯强度。王庆等[55]研究了层冰与具有T 型材的板的作用，模型中的船体板采用键基近场动力学建模，T 型材假定为刚体，冰采用弹脆性本构模型，如图16 所示。

图16 具有T 型材的板在冰作用下的变形[55]Fig. 16 Deformation of plate with T-section under ice interaction[55]

Nguyen 等[56]建立了键基近场动力学的六自由度梁模型，该模型可以用于各种梁结构，包括直梁和曲梁，并模拟了受海洋载荷的导管架平台的响应以及船舶与导管架平台的碰撞过程，捕获了作用过程中可能发生的损伤，如图17 所示。

在上述工作中，Gao 等[53]采用的复合材料模型是对特种船用板材较好的尝试，但依然处于理论研究和模型展示阶段。在其他研究中也有较为接近工程应用的板材结构，例如桁架、型材等，这些都是在海洋工程应用方面的首次尝试。未来的研究重点可以着重于材料的经典力学本构模型在态基近场动力学框架下的实现，从而模拟更加复杂的材料行为，参考基于态基近场动力学的材料本构的相关研究[47,57]。

4.2 在水下爆炸破冰中的应用

水下爆炸破冰的过程十分复杂，影响其效果的因素很多，例如冰层的力学性质、外部环境（例如温度、周围基础设施、天气状况等）、水的流动、药包重量、冰层厚度以及药包的冰下距离等。如果通过实验去研究这些因素的影响，无疑要进行大量的反复实验，实验成本非常巨大，而且还需考虑实验周期、人力成本投入、实验环境和设施的控制，以及实验的安全性等因素。此时，数值模拟的巨大优势就得以体现，通过数值模型，可以在较短的时间内、较低的成本投入和较高的安全下得到合理、可靠的分析结果。

Wang 等[27,58]建立了水下爆炸破冰近场动力学计算模型（图18），分析了水下爆炸破冰的过程，以及冰层裂纹形成、扩展和分叉的特点与规律，并将数值模拟结果与实验数据进行对比，验证了数值模型的准确性。同时，其还从定量和定性的角度研究了影响水下爆炸破冰的参数，例如材料参数（密度、断裂韧度、弹性模量）、冰层开孔大小、模型参数（药包重量、药包冰下深度、冰层厚度）对破冰效果和裂纹扩展的影响。但该工作只考虑了冰下爆炸载荷冲击波的部分作用，未考虑气泡的作用。

基于上述工作，程文霞[59]提出了几种气泡加载方式，例如球状气泡和镜像气泡载荷，并将其与冲击波联合作用，从而使冰下爆炸载荷的相关研究内容更完整、全面。模拟结果如图19 所示。

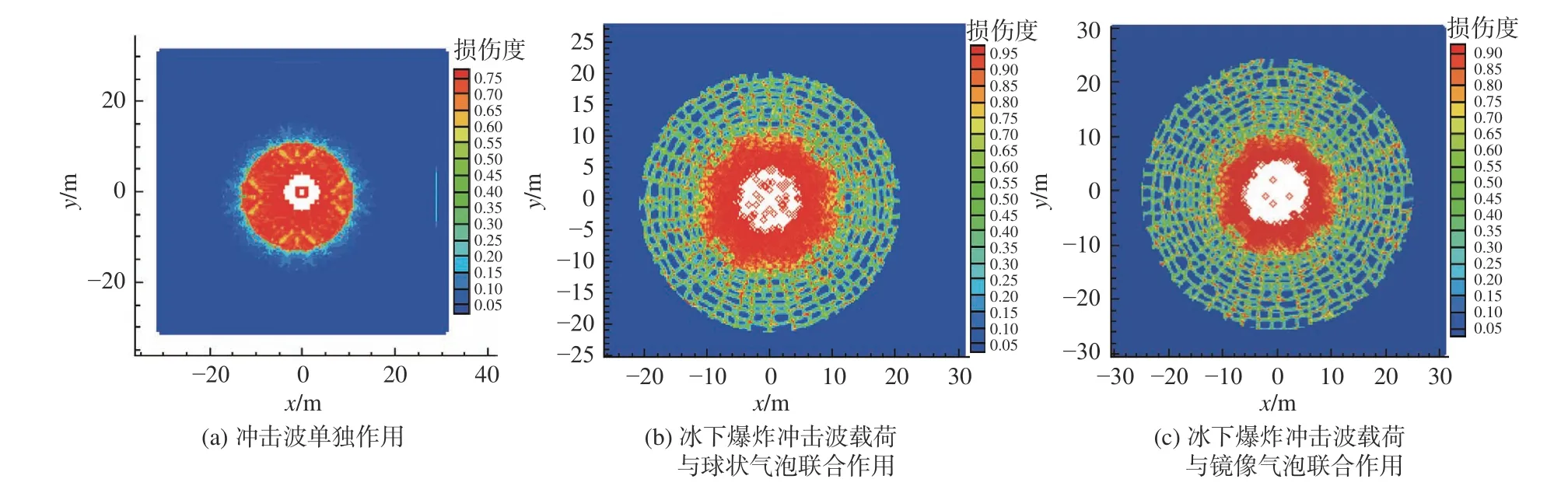
图19 冰下爆炸破冰数值模拟结果图[59]Fig. 19 Simulation of ice breaking under explosion[59]

基于爆炸载荷的特性，从冲击与应力波相互作用的角度分析破冰机理是一个重要的研究方向。由于键基理论没有应力/应变的概念，因此，未来可以利用态基近场动力学理论开展相关工作，同时建立基于应力波理论的破坏准则等。

4.3 在结构物表面除冰中的应用

在湿冷的海雾、暴风雪等极端气候下，会形成附着于极地船舶和海洋平台上的海冰，这给极地装备的正常工作造成了极大威胁。极地船舶和海洋平合上的覆冰会对船舶的适航性和海洋平台的稳定性造成影响，尤其是对于上层建筑高大的极地船舶，由覆冰引起的船舶重心的提高和阻力的增大可能会导致极地船舶与海洋平台的倾覆；船舶和海洋平台上电线、电缆、雷达等无线电设备上的覆冰将会影响通讯信号的接收。为研究结构除冰问题，Song 等[60-61]采用近场动力学方法对铝板除冰涉及的热力耦合问题进行了模拟，脉冲载荷作用下的模拟结果如图20 所示。其中，冰采用的是由键基近场动力学模型建立的弹−脆性材料，考虑热力学的影响，研究了冰在升温过程中的开裂等特性。此外，还对由热载荷所引起的冰裂纹的特征予以了讨论。但是，该模拟结果尚未得到实验结果的验证，另外，冰−铝界面处键刚度的取值也缺少充足的理论支撑。

图20 脉冲载荷作用下铝板表面覆冰破坏模拟[60]Fig. 20 Simulation of failure of ice coating on aluminum plate surface under pulse load[60]

5 结 语

近场动力学方法在冰区船舶与海洋工程的应用中存在巨大潜力，相关研究尚处于起步阶段。未来，研究的重点应为冰的本构模型、冰−水耦合模型及海洋结构物材料模型。

1） 冰的本构模型应根据应用场景的不同而不同。例如，在船−冰作用过程中，冰经常作为弹−脆性材料处理，但是在船体不同部位冰的破坏形式不同，例如在船艏部位冰的破坏模式主要为弯曲破坏，在船肿部位冰破坏模式主要为压缩破坏，因此，相应地冰的材料模型应能同时反映弯曲破坏和压缩破坏等特性。在结构物桩腿与冰的作用中，蠕变和韧性变形是需要重点关注的内容，目前尚未有采用近场动力学方法对此类问题的相关研究。

2） 冰−水相互作用实际上是流体−结构的相互作用，大量的文献为研究流体与冰的耦合提供了策略，本文介绍的耦合模型在原理上没有创新。耦合的方法有多种，考虑到工程应用，仍需进行大量研究。例如，在层冰−水耦合问题中，层冰破碎为小块冰，小块冰之间的碰撞涉及多体多自由度运动，对计算机的性能要求较高。未来，可借助物理引擎或其他水动力数值方法，如格子玻尔兹曼方法（lattice Boltzmann method，LBM）。

3） 海洋结构物在极端环境下面临破坏的可能，不同于一般的力学问题，大变形和断裂是该过程中2 个典型的特点。研究结构的变形，借助有限元方法是当前最好的选择，目前已有多款可供选择的商用软件并已得到广泛验证。涉及到结构破坏时，将经典连续介质力学的材料本构模型嵌入态基近场动力学框架中，可以实现模拟材料的复杂行为。为满足工程应用，可以采用近场动力学−有限元耦合的方法，在将要破坏的区域采用近场动力学模型，其他区域则采用有限元模型，从而提高计算效率。