带缝钢板剪力墙纵向自由边加劲性能有限元分析

张 飞

(健研检测集团有限公司,福建 厦门 361004)

0 引 言

带缝钢板剪力墙(Steel Plate Shear Wall with Slits,简称SPWS)最早是由日本九州大学的Toko Hitaka和Chiaki Mastsui教授提出的[1]。如图1所示,是指用激光在钢板上按一定间距开设宽度约10 mm的竖缝,并利用竖缝间小柱变形耗能的一种新型的抗侧力耗能构件。大量的实验研究和数值分析表明SPWS具有可调的初始抗侧向刚度、较高的承载力、良好的延性变形和抗震耗能能力。但在实际工程应用中,为方便门、窗洞口的灵活布置和减小因附加弯矩对主框架钢柱造成的不利影响,通常带缝钢板剪力墙的上、下两端用高强螺栓或焊缝与梁连接,而带缝钢板剪力墙的左右两纵向自由边则与主框架柱分开布置,详见图2。实际受力时带缝钢板剪力墙左右两纵向自由边常因边界约束不足容易导致整体失稳,导致带缝钢板剪力墙整体优异性能得不到充分的发挥,因此需要对其纵向自由边进行加劲设计并提出相应设计指标。

图1 SPWS构造示意图

图2 工程实例

1 加劲肋对SPWS的影响及其布置方式

由于带缝钢板剪力墙的高度接近房屋层高,高度约为3 m,宽度为2～3 m,剪力墙高宽相差不大,因此不能按照一般的工字梁翼缘的方法进行纵向自由边加劲肋设计,通常借鉴对受剪梁腹板弹性屈曲的研究。[2]国内外部分学者对此进行了相关研究,结果表明,带缝钢板剪力墙纵向自由边加劲肋对剪力墙的受力性能有如下影响:

(1) 纵向自由边加劲肋对带缝钢板剪力墙的抗侧向刚度影响较小,对带缝钢板剪力墙是否进行纵向自由边加劲或改变加劲肋的结构形式,则剪力墙的抗侧向刚度变化不明显,可忽略不计。

(2) 纵向自由边加劲肋可显著提高带缝钢板剪力墙的抗剪承载力[3],且进行纵行自由边加劲后,带缝钢板剪力墙的荷载—位移曲线明显趋于平缓,延性显著提高。

(3) 纵向自由边加劲肋使得带缝钢板剪力墙最大面外变形从两侧往中间移,不仅改变了带缝钢板剪力墙的屈曲模式,而且还减少了剪力墙面外屈曲变形幅值,明显提高带缝钢板剪力墙延性,且可显著减少对外包混凝土的斥力作用,避免混凝土提前脱落,使二者可更好地协同工作。

(4) 纵向自由边加劲肋使得带缝钢板剪力墙的滞回曲线更饱满,明显提高了带缝钢板剪力墙的抗震耗能能力。

(5) 纵向自由加劲肋应沿带缝钢板剪力墙通高布置[4],否则带缝钢板剪力墙容易发生角部局部失稳而带动整板提前失稳。

综上,纵向自由边加劲是必要的,且须沿带缝钢板剪力墙通高布置。

2 有限元模型

本研究采用ANSYS软件进行有限元分析。带缝钢板剪力墙模型取自某工程实例,剪力墙构造及相关尺寸参数如表1所示。有限元分析模型的单元类型为SHELL181单元[5];钢材为理想弹塑性材料,屈服强度fy=235 MPa;约束SPWS底部六个自由度,顶部考虑到楼板的作用只约束面外变形Uz和面外转角Rotx、耦合节点的Ux和Uy的自由度;取第一模态为初始缺陷波形,幅值为H/450;在顶部施加均有水平荷载。

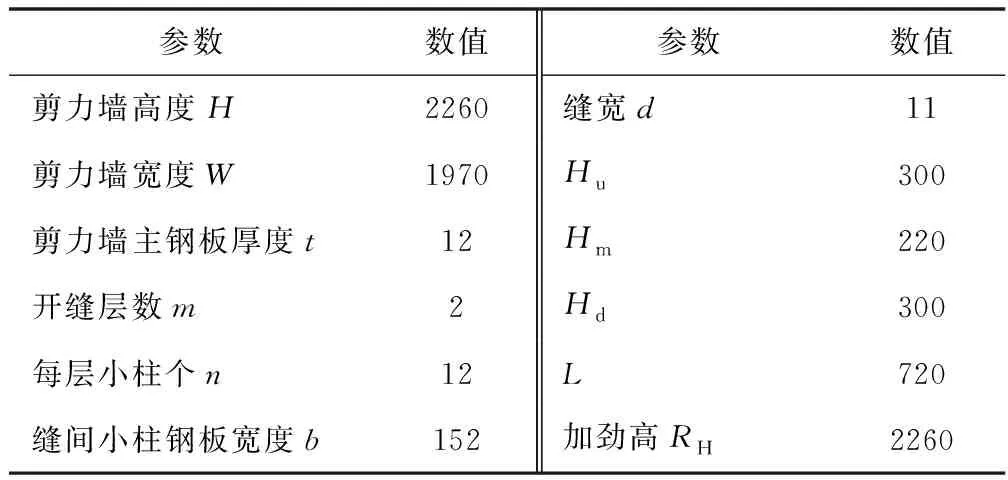
表1 有限元模型外围尺寸及开缝参数(单位:mm)

本研究所用的有限元模型中开缝钢板外围尺寸、厚度及开缝形式不变,变量为纵向自由边加劲的类型及尺寸规格。加劲肋分别选用直板、槽钢和矩形(方)管等三种加劲形式。

3 加劲肋设计及评价指标

3.1 弯曲刚度比η对SPWS性能的影响

纵向自由边加劲肋与开缝钢板剪力墙的布置情况如图3所示。通过借鉴对受剪梁腹板弹性屈曲的研究可知,评价纵向自由边加劲肋与开缝钢板之间相互约束作用的一个重要指标是二者之间的面外弯曲刚度比η。

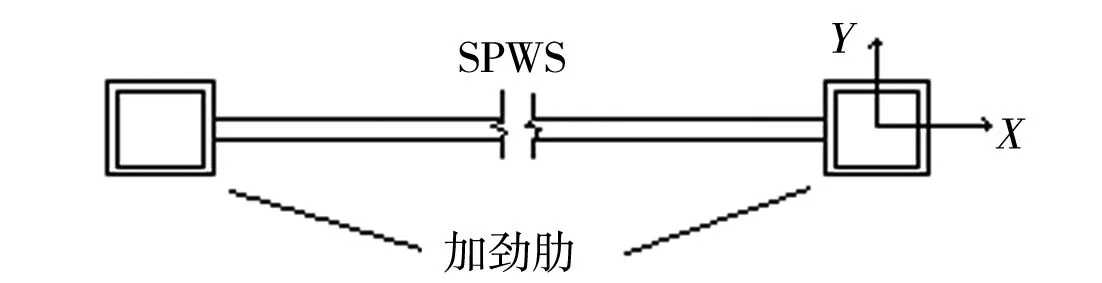
图3 加劲肋布置示意图

η计算公式如下:

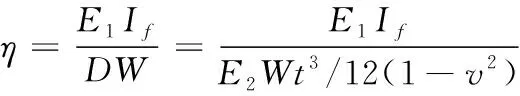
(1)

式中:If为纵向自由边加劲肋(左右两个)绕X轴(平面外)的抗弯惯性矩;D为开缝钢板的面外弯曲刚度。由于每个开缝宽度较小,约为10 mm,因此可采用相应未开缝剪力墙的面外刚度代替。E1、E2分别为纵向自由边加劲肋和开缝钢板弹性模量,为保证实际工程应用焊接质量的可靠性,一般选同种材料,即E1=E2。为详细研究左右两个纵向自由边加劲肋和开缝钢板平面外弯曲刚度比η对剪力墙性能的影响,特建立包括直板、槽钢和矩形(方)管等三种加劲形式共计25个ANSYS有限元模型,各模型的纵向自由边加劲肋截面尺寸及相关物理指标见表2。

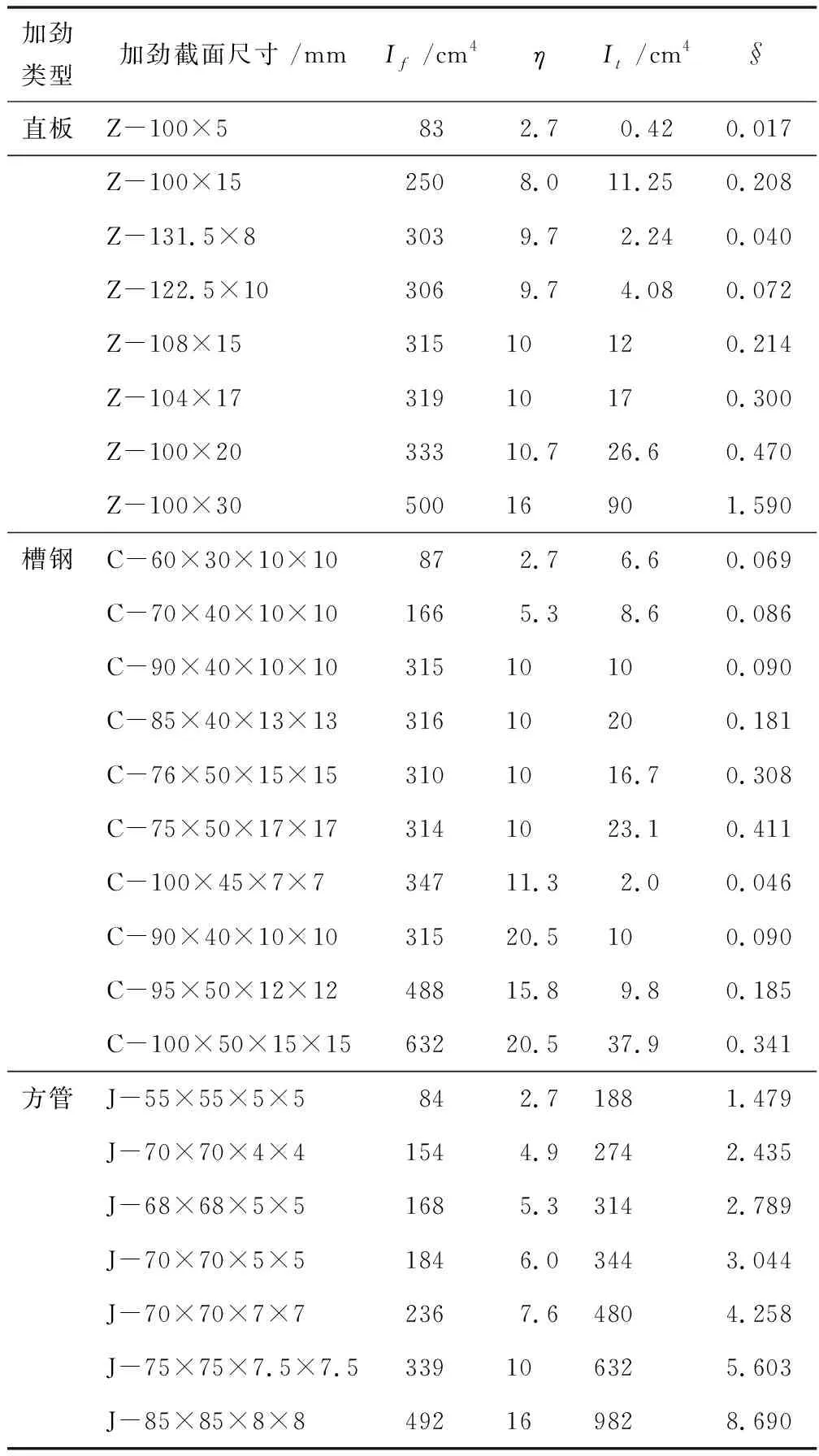
表2 加劲截面尺寸及相关物理指标

2.It为单加劲肋的扭转刚度;§为加劲肋与带缝钢板扭转刚度之比(影响详见下文分析)。

图4为三种加劲形式下不同面外弯曲刚度比η对应的带缝钢板剪力墙荷载-位移曲线。

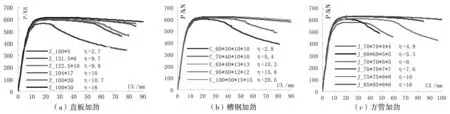
图4 三种加劲形式下不同弯曲刚度比η对应的荷载-位移曲线

由图4可知:

(1) 无论对于哪种纵向自由边加劲结构形式,随着面外弯曲刚度比η的增加,带缝钢板剪力墙的初始刚度(曲线斜率)变化并不明显。

(2) 无论对于哪种纵向自由边加劲结构形式,随着面外弯曲刚度比η的增加,带缝钢板剪力墙的最大承载力不断增加。

(3) 无论对于哪种纵向自由边加劲结构形式,随着面外弯曲刚度比η的增加,带缝钢板剪力墙的荷载-位移曲线趋于平缓,延性变形能力显著增加。但当η≥10时,随着η的增加,带缝钢板剪力墙的最大承载力、延性性能变化反而并不明显,因此取纵向自由边加劲肋和开缝钢板平面外弯曲刚度比η=10作为纵向自由边加劲弯曲刚度的设计依据。

3.2 扭转刚度比§对SPWS性能的影响

在试验研究和有限元分析的过程中发现带缝钢板剪力墙同时沿纵轴(Y轴)发生扭转现象。图5为方管通高加劲的有限元模型在剪力墙层间转角等于1/54时的Roty位移云图。

图5 层间位移角1/54时Roty位移云图

由5图可知,带缝钢板剪力墙在纵向自由边缘加劲处存在一定程度绕Y轴的扭转变形。说明剪力墙纵向自由边加劲需保证具有一定的扭转刚度,因此纵向自由边缘加劲肋与钢板剪力墙的扭转刚度比也应成为评价加劲性能的一个重要指标。为此特引进参数扭转刚度比§。

§计算公式定义如下:

(2)

式中:It1、It2分别为两个纵向自由边加劲肋与主钢板墙的自由扭转惯性矩,由于开缝宽度不大,可采用相应的未开缝剪力墙的自由扭转刚度代替;G1、G2分别为加劲肋和开缝钢板的剪切模量,为保证实际应用中焊接质量可靠,一般选同种材料,即G1=G2。

图6反映了直板和槽钢两种不同加劲肋条件下,扭转刚度比§对带缝钢板剪力墙荷载-位移曲线和面外变形的影响。由图6可知,虽然当弯曲刚度比η较大时,但若扭转刚度比§较小,带缝钢板剪力墙优异的性能同样得不到充分发挥,因此不能把弯曲刚度比η作为评价加劲影响的唯一指标。

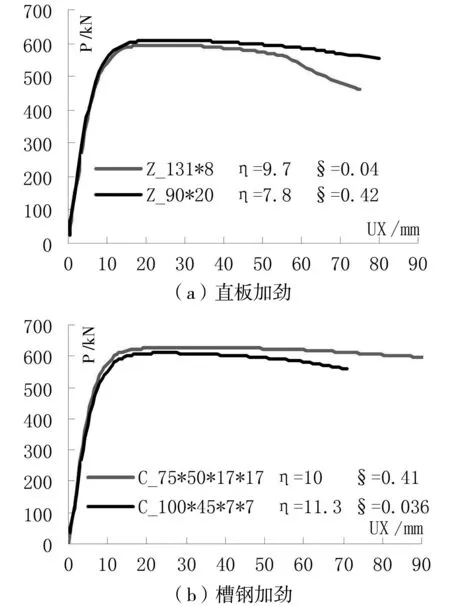
图6 不同加劲形式下§对荷载-位移曲线的影响

图7为当弯曲刚度比η相同,不同的扭转刚度比η对带缝钢板剪力墙荷载位移-曲线的影响。由图7可知,在弯曲刚度比η相同的情况下,随着扭转刚度比§的增加,纵向自由边加劲肋的性能则更加优越。因此必须考虑扭转刚度比§的影响,并对其加以定量分析。

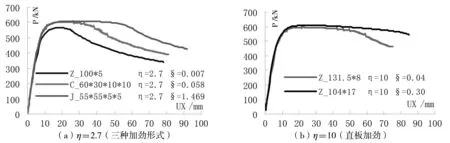
图7 扭转刚度比§对SPWS荷载-水平位移曲线的影响

图8和图9分别为三种加劲情况下弯曲刚度比η和扭转刚度比§对荷载-水平位移曲线的影响和当层间位移角等于1/57时直板加劲对SPWS面外位移的影响。可知当面外弯曲刚度比η≥10,扭转刚度比§≥0.3时,带缝钢板剪力墙的荷载-位移曲线变化较为平缓、面外变形显著减少,即加劲肋的设计能够满足对钢板墙的约束要求。但是当再提高各种加劲的弯曲刚度比η和扭转刚度比§的值时,带缝钢板剪力墙的荷载-位移曲线和面外位移相差不大,因此试图再通过增大η、§来提高SPWS的延性和减少面外位移是不经济的。

图8 η和§对SPWS的荷载-位移曲线的影响

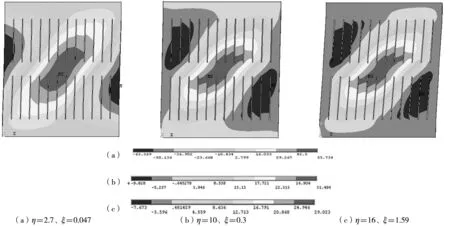
图9 η、§对SPWS面外位移的影响(1/57、直板加劲)

综上,当开缝层数为m=2时,纵向自由边加劲的设计应满足η≥10和§≥0.3两个条件,且不应试图通过不断提高η、§的值来进行加劲设计。

3.3 轴向刚度比对SPWS性能的影响

在试验研究和有限元分析的过程中,同样发现带缝钢板剪力墙同时沿纵轴(Y轴)发生平动变形现象。图10为方管通高加劲的有限元模型在剪力墙层间转角等于1/54时的Uy位移云图。说明剪力墙纵向自由边加劲需保证具有一定的轴向刚度。大量的有限元分析表明,当面外弯曲刚度比η≥10和扭转刚度比§≥0.3时,剪力墙纵向自由边加劲的轴向刚度亦能满足要求。

图10 层间位移角为1/54 时UY位移云图

4 加劲肋的结构选型

由上文分析可知,加劲肋需要满足一定的弯曲刚度、扭转刚度和轴向刚度的要求,且由于墙体要保持一定的厚度,因此带缝钢板剪力墙纵向自由边加劲肋的截面不宜太宽,并且若将一狭长直板焊接在主钢板墙上会造成该直板加劲的焊接变形不宜控制。同时通过对型钢如T形板、槽钢、工字钢、矩形(方)钢管加劲模型的有限元分析表明型钢加劲效果较好。由图11可知,若采用冷弯矩形(方)钢管作为边缘加劲,由于矩形(方)管加劲截面闭合,当面外弯曲刚度满足时,扭转刚度和轴向刚度也会满足要求,因此矩形(方)管是较为理想的加劲类型。

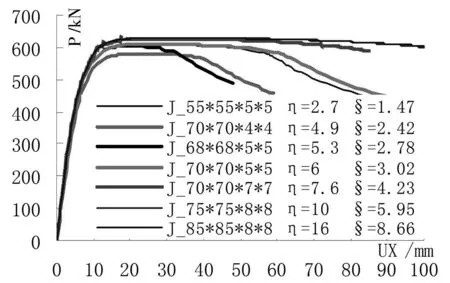
图11 不同方管加劲对荷载-位移曲线的影响

5 加劲肋与SPWS的连接方式

型钢加劲,特别是矩形(方)管作为理想的加劲类型。但由于加劲长度较大(一般大于2 m),且为空间封闭截与主钢板墙的焊接属于“以小焊大”,若连续施焊,可能会造成较大的焊接残余变形和高额的残余应力,因此应采取连续焊,中间分段交错断续焊的连接方式。

6 结 论

纵向自由边加劲肋对带缝钢板剪力墙的整体性能发挥起到关键作用,由上述分析可知对纵向边缘加劲的设计应根据以下原则:

(1) 须采取加劲措施且应沿剪力墙纵向自由边通高布置。

(2) 加劲肋设计时不能仅考虑面外弯曲刚度比η的影响,必须同时考虑扭转刚度比§和轴向刚度比的作用。当开缝为两排时,加劲肋按η≥10、§≥0.30进行设计,且不应试图通过不断提高η、§的值来提高剪力墙的整体受力性能。

(3) 加劲肋形式宜为型钢。且基于而矩形(方)管加劲截面闭合,当面外弯曲刚度比η满足时,扭转刚度和轴向刚度通常满足要求,因此矩形(方)管加劲效果较好。

(4) 加劲肋与钢板墙宜采取分段交错断续焊的方式连接。